Центральные и вписанные углы - определение и вычисление с примерами решения

Содержание:

Центральным углом называют угол с вершиной в центре окружности.

На рисунке 79

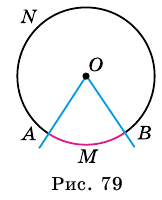
Если центральный угол больше развернутого, то соответствующая ему дуга больше полуокружности. Развернутому углу соответствует дуга, являющаяся полуокружностью. Дугу обозначают символом 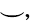который записывают перед названием дуги или над ним. Чтобы уточнить, о какой именно из двух дуг, на которые центральный угол разделил окружность, идет речь, на каждой из них отмечают произвольную точку, отличную от концов дуги. 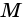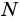Например, и (рис. 79). 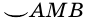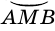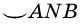Тогда эти дуги можно записать так: (или ) и (или 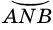). Если понятно, о какой именно дуге идет речь, то для ее обозначения достаточно указать лишь концы дуги, например 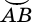(или ).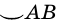

Дугу окружности можно измерять в градусах.

Градусной мерой дуги окружности называют градусную меру соответствующего ей центрального угла.

Например, если 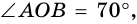 то 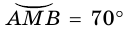 (рис. 79).

Очевидно, что градусная мера дуги, являющаяся полуокружностью, равна 180°, а дуги, являющейся окружностью, - 360°. На рисунке 79: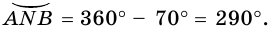

Что такое вписанный угол

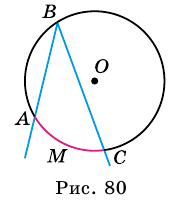
Вписанным углом называют угол, вершина которого лежит на окружности, а стороны пересекают эту окружность.

На рисунке 80 стороны вписанного угла 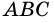 пересекают окружность в точках 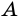и 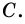 Говорят, что этот угол опирается на дугу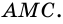

Очевидно, что точки пересечения сторон вписанного угла с окружностью делят ее на две дуги. Той, на которую опирается вписанный угол, будет дуга, не содержащая его вершину. Например, на рисунке 80 стороны вписанного угла 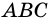делят окружность на две дуг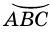и: и 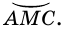Так как  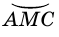не содержит вершины угла (точки 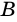), то является дугой, на которую опирается вписанный угол  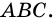Эта дуга выделена цветом.

Теорема (о вписанном угле). Вписанный угол измеряется половиной дуги, на которую он опирается.

Доказательство:

Пусть 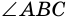является вписанным в окружность с центром 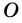и опирается на дугу 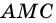(рис. 80).

Докажем, что 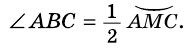 Рассмотрим три возможных положения центра окружности относительно вписанного угла.

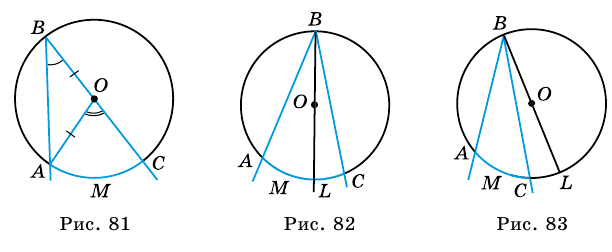
1) Пусть центр окружности - точка 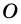- принадлежит одной из сторон угла, например 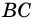(рис. 81). Центральный угол 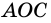является внешним углом треугольника  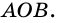Тогда, по свойству внешнего угла, 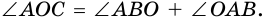Но 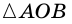- равнобедренный ( 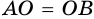как радиусы), поэтому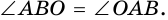

Следовательно, 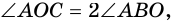 то есть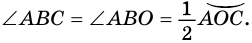

Но 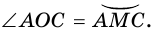 Таким образом,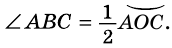

2) Пусть центр окружности лежит внутри вписанного угла (рис. 82). Проведем луч 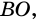пересекающий окружность в точке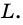

Тогда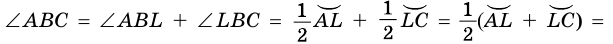

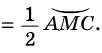
3) Пусть центр окружности лежит вне вписанного угла

(рис. 83). Тогда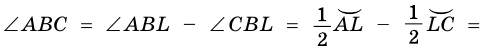

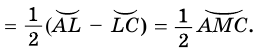
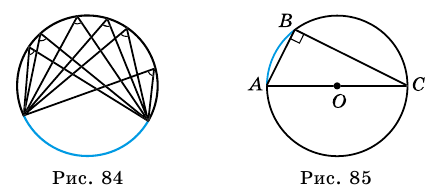
Следствие 1. Вписанные углы, опирающиеся на одну и ту же дугу, равны (рис. 84).

Следствие 2. Вписанный угол, опирающийся на диаметр, — прямой (рис. 85).

Пример:

Докажите, что угол с вершиной внутри круга измеряется полусуммой двух дуг окружности, одна из которых лежит между сторонами угла, а вторая - между их продолжениями.

Доказательство:

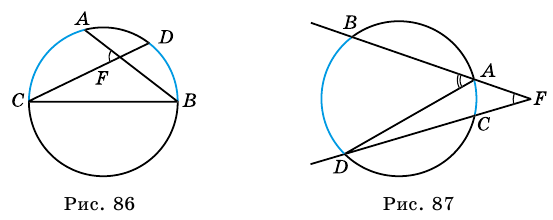
Рассмотрим 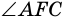 с вершиной внутри круга (рис. 86). Докажем, что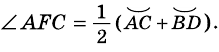

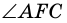- внешний угол треугольника 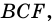поэтому:

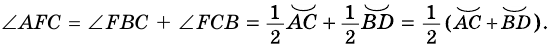
Пример:

Докажите, что угол между двумя секущими, пересекающимися вне круга, измеряется полуразностью большей и меньшей дуг окружности, лежащих между его сторонами.

Доказательство:

Рассмотрим 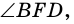 вершина которого лежит вне круга, a 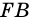и 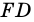- секущие (рис. 87). Докажем, что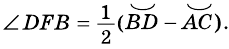 

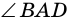- внешний угол треугольника  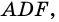поэтому:

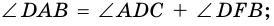 то есть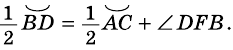

Поэтому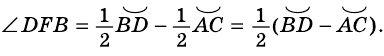

А еще раньше...

Доказательство теоремы о вписанном угле встречается в «Началах» Евклида. Но еще раньше этот факт, как предположение, впервые высказал Гиппократ Хиосский (V в. до н. э.).

О том, что вписанный угол, опирающийся на диаметр, является прямым, было известно вавилонянам 4000 лет тому назад, а первое доказательство этого факта приписывают Фалесу Милетскому.

Смежные и вертикальные углы

Два угла называют смежными, если одна сторона у них общая, а две другие являются дополняющими лучами. На рисунке 262 углы 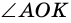и 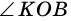- смежные.

Свойство смежных углов. Сумма смежных углов равна 180°.

Два угла называют вертикальными, если стороны одного из них являются дополняющими лучами сторон другого.

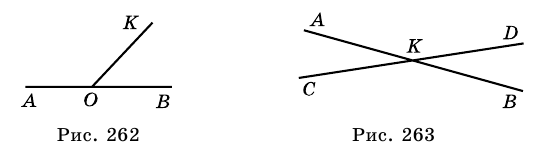
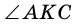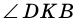На рисунке 263 и  - вертикальные, углы  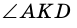и 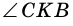также вертикальные.

Свойство вертикальных углов. Вертикальные углы равны.

Свойства углов, образованных при пересечении параллельных прямых секущей

1. Соответственные углы, образованные при пересечении параллельных прямых секущей, равны.
2. Внутренние накрест лежащие углы, образованные при пересечении параллельных прямых секущей, равны.
3. Сумма внутренних односторонних углов, образованных при пересечении параллельных прямых секущей, равна 180°.