Центральная предельная теорема в теории вероятности с примерами решения

Содержание:

Центральная предельная теорема:

Формулировка центральной предельной теоремы (для одинаково распределенных слагаемых).

Пусть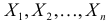

сколь угодно близок к нормальному закону распределения.

В условиях теоремы имеет место предельное соотношение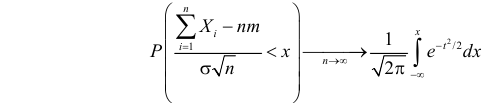

где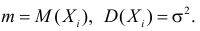

Пример:

Стрелок в десятку попадает с вероятностью 0,4, в девятку – с вероятностью 0,3, в восьмерку – с вероятностью 0,2, в семерку – с вероятностью 0,1. Какова вероятность того, что при 25 выстрелах стрелок наберет от 220 до 240 очков?

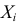Решение. Пусть при м выстреле стрелок выбивает очков. Величины 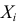независимы и имеют одно и то же распределение

Заметим, что 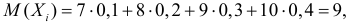а ( ) .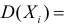

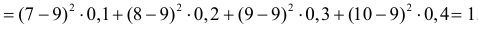Сумма очков 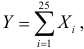будучи суммой большого числа независимых одинаково распределенных слагаемых с ограниченными дисперсиями, имеет закон распределения близкий к нормальному с параметрами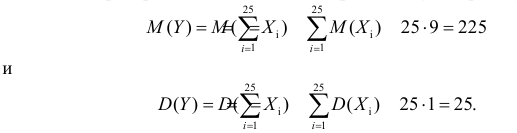

В итоге 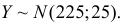Поэтому по формуле (2.9.2)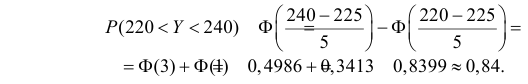

Ответ.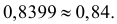 

Пример:

Регулировка прибора занимает время от 4 до 10 мин. Регулировщику предстоит отрегулировать 50 приборов. Считая для каждого прибора равновозможными все значения времени регулировки в указанных пределах, оценить вероятность того, что регулировщик справится с работой за шесть часов.

Решение. Пусть 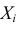– время регулировки 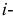го прибора, а 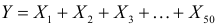– время выполнения работы рабочим. Требуется найти 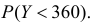Величина Y является суммой большого числа одинаково распределенных независимых случайных величин, каждая из которых ограничена. По центральной предельной теореме Y имеет закон распределения близкий к нормальному закону распределения. Найдем параметры этого закона, т.е. математическое ожидание и дисперсию величины Y. Так как случайные величины 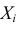независимы, то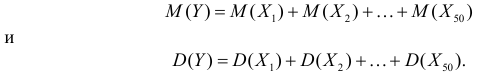

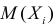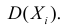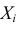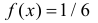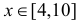Вычислим и По условию все значения случайной величины равновозможны в отрезке [4,10]. Поэтому функция плотности вероятности этой случайной величины в указанном отрезке постоянна. Чтобы площадь, заключенная между графиком функции плотности вероятности и осью абсцисс, равнялась единице, следует положить при и 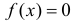при остальных 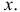С учетом этого имеем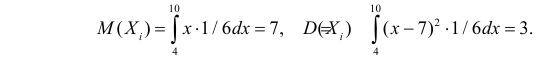

Поэтому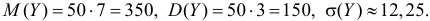 

Итак, 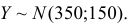Для вычисления искомой вероятности воспользуемся формулой (2.9.2) и таблицей функции Лапласа (см. прил., табл. П2):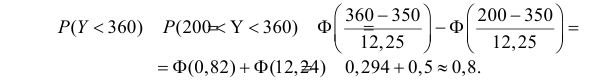

Ответ.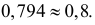 

Пример:

Жетон для игрального автомата стоит 10 рублей. При использовании одного жетона (в отдельной игре) вероятность не получить ничего равна 0,8, вероятность получить 20 рублей равна 0,15, вероятность получения 50 рублей равна 0,04 и вероятность получения 100 рублей равна 0,01. Игрок купил жетонов на 1000 рублей. Какова вероятность того, что игрок не окажется в проигрыше?

Решение. Игрок купил 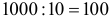жетонов. Результат каждой игры (использование одного жетона) является случайной величиной 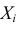с законом распределения

Выигрыш указан с учетом стоимости жетона.

Результат 100 игр обозначим через 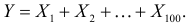Величина Y является суммой большого числа одинаково распределенных независимых случайных величин, каждая из которых ограничена. По центральной предельной теореме Y имеет закон распределения близкий к нормальному закону распределения. Найдем параметры этого закона, т.е. математическое ожидание и дисперсию величины Y. Так как случайные величины 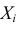независимы, то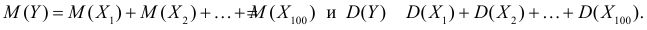

Так как

 

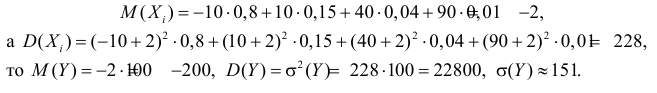
Итак, Y имеет примерно нормальный закон распределения Игрок не окажется в проигрыше, если По формуле (2.9.2) имеем

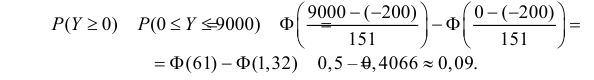
Ответ.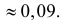 

Пример:

Вероятность рождения мальчика равна 0,514. Определить вероятность того, что доля мальчиков среди 400 новорожденных будет отличаться от вероятности рождения мальчика не более чем на 0,05 в ту или другую сторону.

Решение. Рождение ребенка можно рассматривать как независимый опыт с вероятностью «успеха» 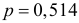(по данным статистики на каждую тысячу новорожденных приходится 514 мальчиков). Тогда по формуле (2.13.1)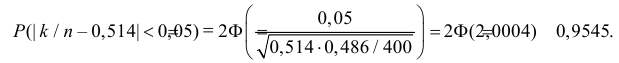

Ответ. 0,9545.

Пример:

Вероятность события 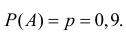Сколько независимых опытов нужно проделать, чтобы с вероятностью 0,95 быть уверенным, что частота появления события в этих опытах будет отличаться от вероятности события не более чем на 0,05 в ту или другую сторону?

Решение. Запишем формулу (2.13.1) для нашего случая: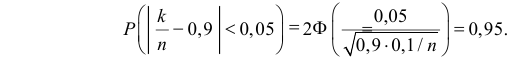

По таблице функции Лапласа находим, что 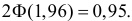Поэтому 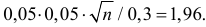Откуда 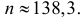Условия задачи выполняются при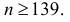

Ответ.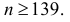 

Центральная предельная теорема. Систематические изменения или случайность

Мы уже знаем, что нормальное распределение - особенное. Некоторые его свойства мы сможем использовать и для распределений, которые, строго говоря, нормальными не назовешь. Задача, которую мы рассмотрим в этом разделе имеет чрезвычайно важное значение для бизнеса, это задача о диагностировании тенденций к изменению показателей.

Удобство использование нормального распределения некоторых случайных величин и особые возможности, которые закон нормального распределения предоставляет исследователю, породили ряд теорем, которые позволяют пользоваться этими свойствами даже, если генеральная совокупность представляет собой "не вполне нормальное распределение".

Центральная предельная теорема имеет несколько формулировок, мы не будем их здесь полностью приводить и доказывать. Для нас важно знать только то, что в большинстве случаев среднее арифметическое выборки, взятой из генеральной совокупности (напомним, что это среднее арифметическое - тоже случайная величина), ложится на нормальное распределение гораздо лучше, чем исходная генеральная совокупность.

Другими словами, если мы возьмем несколько выборок из генеральной совокупности, то средние арифметические величины этих выборок будут представлять собой новую случайную величину с практически нормальным распределением. Именно эта теорема и позволит нам проверять так называемые статистические гипотезы, т.е. делать заключение о наличии тенденции к изменению показателей деятельности, которые сами по себе, являясь случайными величинами, имеют право на некоторый разброс.

Пример:

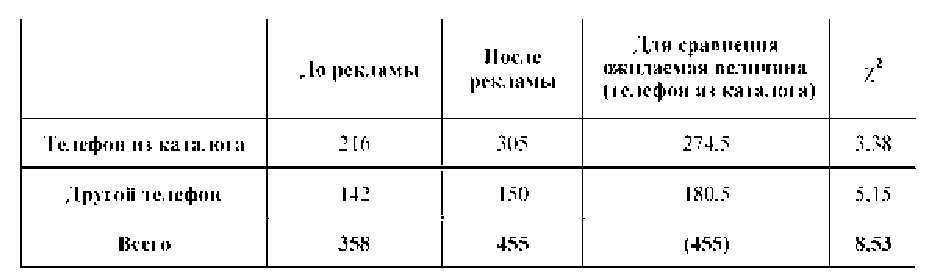
Фирма поместила информацию о своей продукции в каталоге. Был указан один из двух номеров телефона отдела продаж, на который и раньше поступали звонки потенциальных покупателей. Другой номер телефона в каталоге не упоминался. За два месяца до выхода каталога и в течение двух месяцев после было зарегистрировано следующее количество звонков на эти телефоны (два столбца в таблице). Как нам определить, подействовала ли информация, данная в каталоге, или мы имеем дело со случайным оживлением на рынке, а деньги на рекламу потрачены напрасно?

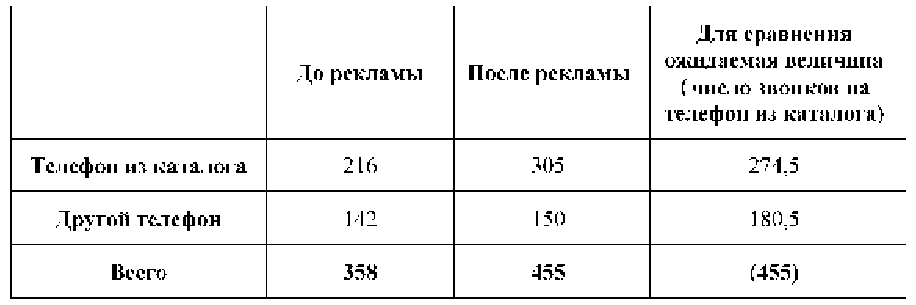
Последний столбец в таблице - ожидаемые величины. Это наши оценки, сделанные из предположения, что ничего не изменилось, и реклама не оказала никакого действия, т.е. произошло общее оживление на рынке и больше ничего, а пропорции между числом звонков на оба телефона должны сохраниться в точности. {Ожидаемая величина для телефона из каталога} = 455r216/358=274,5 {Ожидаемая величина для другого телефона} = 455r142/358=180,5. Наше предположение, о том, что реклама не оказала никакого воздействие на изменение числа покупателей, носит название нулевой гипотезы. Альтернативная гипотеза заключается в предположении о наличии такого влияния. Наша задача - выбрать более достоверную из двух этих гипотез. Чтобы оценить, насколько значимы отклонения реальной ситуации от ожидания по нулевой гипотезе, для обоих телефонов мы должны посчитать величину:

поставить их в таблицу и просуммировать.

Дальнейшие наши действия - определить, с какой вероятностью посчитанные отклонения "ложатся" на соответствующую кривую. Для такой оценки можно воспользоваться значениями так называемого 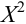-критерия Пирсона. Обычно эти значения задаются в виде стандартных таблиц в книгах по статистике. Дадим и мы такую таблицу (X-греческая буква "хи"):

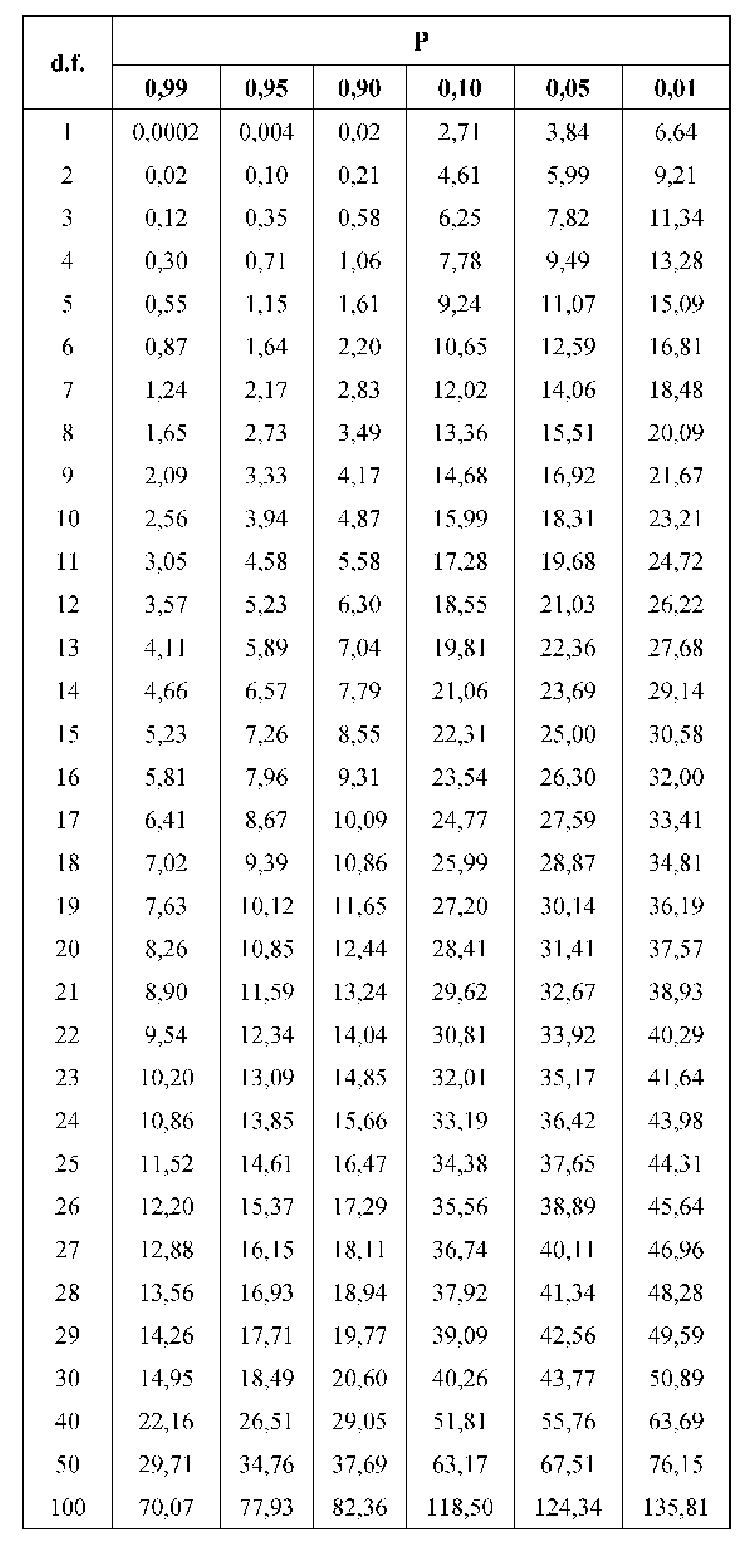
Теперь несколько слов о том, как пользоваться этой таблицей. Буквы d.f. означают число степеней свободы.

Чтобы посчитать степени свободы нужно просто брать в таблице с исходными данными количество строк n и столбцов m, и посчитать величину 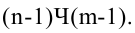Это и будет количество степеней свободы в каждом конкретном случае. Правда, строки и столбцы берутся только для самих исходных данных, ни строка суммирования (всего), ни столбец подсчета ожидаемых величин при определении степени свободы не учитывается. В нашем случае 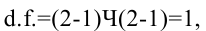это означает, что степень свободы равна единице, и в таблице 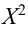мы должны пользоваться соответствующей строкой (верхней).

Теперь о столбцах этой таблицы. Цифры 0,99; 0,95; и т.д. означают, что величины отклонений 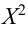, стоящие в этих столбцах с вероятностью 0,99; 0,95; и т.д. возникли случайно. В нашем примере, вероятность случайного происхождения отклонения составляет менее 0,01 (т.е. меньше одного шанса из ста!). Мы вполне можем считать, что реклама оказала воздействие. Обратите внимание, что критерий. 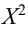не говорит категорически, что случайность тут невозможна, просто вероятность этого очень мала. Другими словами, если мы отбросим нулевую гипотезу и выберем альтернативную, то вероятность ошибки будет меньше одного процента.

Если Вы будете пользоваться этим методом, совсем не нужно считать каждый раз вручную все отклонения. Подсчеты можно проводить в Excel автоматически.

Сначала запишите известные Вам показатели в виде таблицы. Затем посчитайте в Excel столбец ожидаемых величин. После этого нажмите в верхнем меню кнопку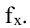

Затем, выберите среди функций тип "статистические", и из предложенного перечня в окошке - ХИ2ТЕСТ.

Затем, по подсказке, поставив курсор в поле "ожидаемый интервал" выделите мышью столбец ожидаемых значений (но не захватывайте сумму в нижней строке). Аналогично в поле "фактический интервал" введите массив из столбика фактических данных после рекламы. Программа сама посчитает граничную вероятность того, что отклонение было случайным.

Так в нашем варианте более точное значение вероятности составляет примерно 0,0035. В таблице мы попали по значению 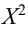между столбцами и посчитать вероятность с такой точностью не смогли. Видимо для того, чтобы Вы привыкли пользоваться подобными оценками, имеет смысл обсудить вопрос о "степени свободы". Что это такое и какие степени свободы вообще могут быть? Понятно, что оценка значимости происходящих изменений может происходить только при наличии данных, как полученных при гипотетическом воздействии этих изменений, так и свободных от изменений.

В качестве заведомо не подверженных изменениям данных в нашем примере выступали показания числа звонков на оба телефона до публикации каталога. Кроме того, для дополнительной объективности данных, мы использовали один телефон как неизвестный в рекламе. Это позволило нам исключить возможное влияние сезонных изменений спроса или другие подобные факторы. В других ситуациях, мы можем сравнивать динамику спроса на один товар с динамикой спроса на другой, если идет целевая раскрутка этого товара, или же товар входит в моду. И в этой ситуации свойства нормального распределения помогут нам сделать вывод о значимости происходящих изменений.

Предельные теоремы теории вероятностей

Сходимость по вероятности

Согласно молекулярно-кинетической теории все газы состоят из большого числа атомов и молекул, которые движутся хаотически в разных направлениях и с разными скоростями. Заранее нельзя указать, где в определенный момент времени, и с какой скоростью будет двигаться та или иная частица. Однако при измерении давления газа измерительный прибор показывает постоянную величину при неизменных внешних условиях. Это показание прибора зависит от числа ударяющихся частиц, от направления их движения и величины скорости частицы. Однако ввиду огромного числа частиц их суммарное действие оказывается постоянным. Этот опыт долгое время использовался как аргумент против молекулярно-кинетической теории. Но, когда был поставлен опыт с “небольшим” числом частиц, то давление при неизменных внешних условиях стало колеблющейся величиной. Этот опыт является иллюстрацией “закона больших чисел”, который будет рассмотрен ниже.

Пусть дана последовательность случайных величин 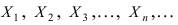и некоторое постоянное число С.

Определение: Сходимостью по вероятности последовательности случайных величин 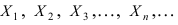к постоянному числу С называется тот факт, когда для любого положительного числа 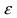имеет место предельное соотношение: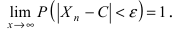

В дальнейшем рассмотрим теоремы, которые устанавливают сходимость некоторых последовательностей случайных величин к постоянному числу. Этими теоремами являются предельные теоремы теории вероятностей. Они разделяются на 2 группы. Первая группа объединяется под общим названием “закон больших чисел”. Эти теоремы доказывают устойчивость средних значений случайных величин и выявляют общие условия, выполнение которых приводит к устойчивости случайных процессов и явлений. Вторая группа теорем получила общее название “центральной предельной теоремы”, которая рассматривает предельные законы распределения. Примером этой группы теорем могут служить дифференциальная и интегральная формулы Муавра-Лапласа, которые были приведены в Лекции № 3. Поэтому в этой Лекции остановимся на теореме Чебышева, которая дает изящную и наиболее общую формулировку “закона больших чисел”.

Неравенство и теорема Чебышева

Прежде, чем рассматривать теорему Чебышева, сформулируем его важное неравенство, которое справедливо как дискретных, так и случайных непрерывных величин.

Теорема: Вероятность того, что отклонение случайной величины X от её математического ожидания по абсолютной величине меньше любого заранее заданного положительного числа 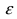, не меньше, чем .

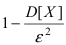Доказательство: Пусть X - случайная дискретная величина, для которой дисперсия равна 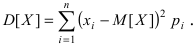В этой сумме отбросим все те слагаемые, для которых выполняется неравенство 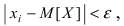и оставим только те слагаемые, для которых выполняется неравенство 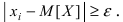В результате этих действий сумма может только уменьшиться, т.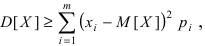е. где 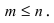Эта сумма еще больше уменьшится, если в ней заменить выражения 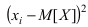на малое число 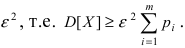В этом неравенстве под знаком суммы стоят вероятности тех значений случайной величины X, для которых выполняется неравенство 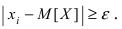Тогда сумма 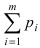по теореме сложения случайных величин есть вероятность того, что случайная величина X принимает значения, при которых выполняется неравенство 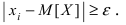Следовательно, выполняется равенство: 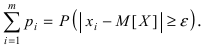Вероятность противоположного события равна 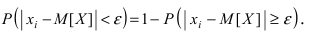Подставив полученное равенство в неравенство для дисперсии, получим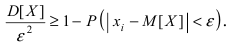

Отсюда и следует неравенство Чебышева. Аналогично теорема доказывается для случайной непрерывной величины.

Используя полученное неравенство, докажем теорему Чебышева:

Теорема: Пусть случайные величины 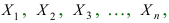... попарно независимы, а их дисперсии ограничены (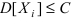). Тогда для любого заранее заданного положительного числа 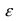имеет место неравенство 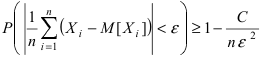что иначе можно записать в виде

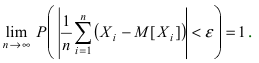
Доказательство: Рассмотрим случайную величину 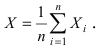Так как по условию теоремы случайные величины 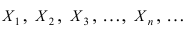попарно-независимы, то математическое ожидание случайной величины X равно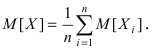

Аналогично для дисперсии имеет место равенство 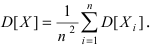Так как по условию теоремы 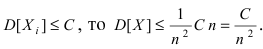Воспользуемся неравенством Чебышева для случайной величины X, т.е.

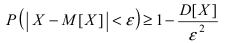или с учетом ограниченности дисперсии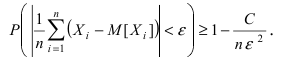

Отсюда следует, что при неограниченном росте 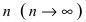вероятность события, указанного в круглых скобках, будет стремиться к 1, т.е. при 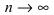указанное событие будет становиться все более достоверным.

Оценка точности и надежности измерений с помощью теоремы Чебышева

Пусть 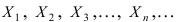результаты n измерений случайной величины X. Очевидно, что 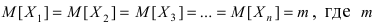- истинное значение случайной величины X. Примем за приближенное значение измеряемой величины среднее арифметическое измеренных значений 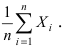Измерение имеет точность 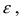если выполняется неравенство 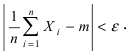Измерение имеет точность 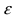с надежностью 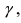если выполняется вероятностное неравенство 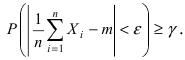Согласно теореме Чебышева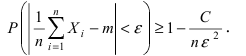

Для выполнения предыдущего неравенство должно выполняться соотношение: Отсюда найдем, какое количество опытов надо провести, чтобы получить заданную точность измерений 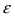с заданной надежностью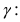

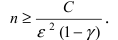
Теорема Ляпунова

В качестве “центральной предельной теоремы" рассмотрим теорему Ляпунова (без доказательства), которая объясняет особое место нормального закона распределения.

Теорема: Если случайные величины 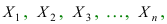... попарно независимы и удовлетворяют условию 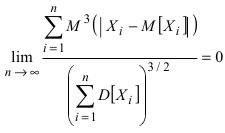, то 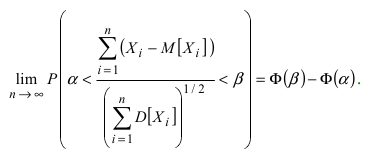Смысл этой теоремы состоит в том, что при достаточно больших значениях n случайная величина 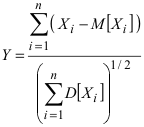распределена почти по нормальному закону распределения с математическим ожиданием 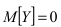и средне-квадратичным отклонением 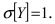“Закон больших чисел” проявляется здесь в том, что несмотря на то, что о слагаемых случайных величинах 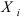почти ничего неизвестно, но об их сумме известно всё, так как определен закон распределения.

Применим эту теорему для оценки точности и надежности измерений. Пусть 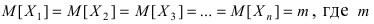- истинное значение случайной величины X, а 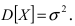Тогда согласно теореме Ляпунова случайная величина

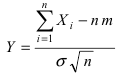
распределена почти по нормальному закону. Так как величины 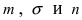не являются случайными, то случайная величина 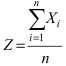распределена также по нормальному закону. Вычислим её математическое ожидание и дисперсию 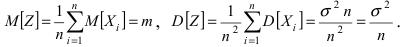Тогда среднее квадратичное отклонение равно 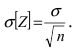Используя формулу вероятности отклонения нормальной случайной величины от ее математического ожидания, получим 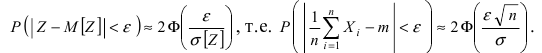Следовательно, чтобы получить заданную точность измерений 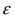с заданной надежностью 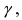надо потребовать выполнение неравенства 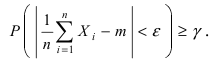Поэтому 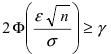или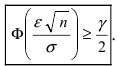

Это неравенство и есть условие достижения заданной точности измерений 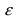с заданной надежностью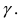

Пример:

Сколько измерений нужно провести, чтобы их среднее арифметическое значение дало измеряемую величину с точностью ε = 0.05 и надежностью γ = 0.9 , если дисперсия измеряемой величины меньше 2 . Необходимое число измерений равно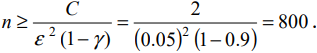

Решение:

По условию задачи точность 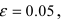надежность 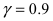и дисперсия измеряемой величины меньше 2. Следовательно, 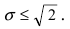Таким образом, согласно теореме Ляпунова должно выполняться неравенство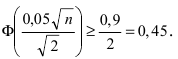

Из таблицы для функции Лапласа находим, что если 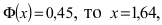следовательно, 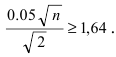Отсюда находим, что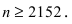

Теорема Бернулли

Пусть проводится n независимых испытаний, в каждом из которых вероятность появления события А постоянна и равна р.

Теорема: Вероятность отклонения частоты m/n от вероятности р в схеме Бернулли на сколь угодно малую положительную величину 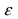стремится к единице при достаточно большом числе испытаний, т.е.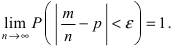

Доказательство: Обозначим через 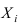, число появлений события А в испытании i. Закон распределения для каждого испытания одинаков и имеет вид: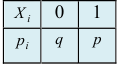

Поэтому математическое ожидание и дисперсия равны: 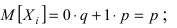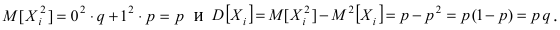В силу того, что 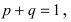то дисперсия 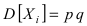ограниченна. Так как испытания независимы, то и случайные величины 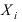также независимы и к ним применима теорема Чебышева, т.е. 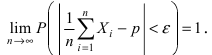Величина 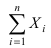дает число случаев, благоприятствующих появлению события А, т.е. равно m, следовательно,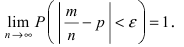

Замечание: Из последней формулы не следует, что 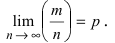Теорема утверждает только тот факт, что вероятность этого события с ростом n стремится к единице.

Замечание: Теорема Бернулли является частным случаем теоремы Чебышева и обосновывает возможность приближенной замены вероятности события A относительной частотой его появления, что находит свое применение в математической статистике.