Центр параллельных сил и центр тяжести в теоретической механике

Содержание:

Система параллельных сил:

Если на тело действуют параллельные силы, не лежащие в одной плоскости (рис. 123), то, выбрав координатные оси так, чтобы ось z была параллельна заданным силам, а плоскость хОу им перпендикулярна, по выражению (49) будем иметь:

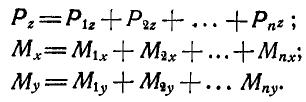
Проекции главного вектора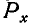

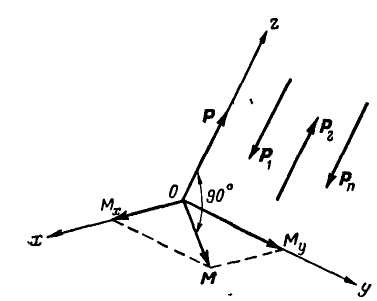
Рис. 123.

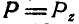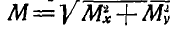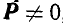Вычисляя по формулам (49а) главный вектор и главный момент , замечаем, что главный вектор Р при выборе центра приведения в точке О расположен на оси z, а главный момент М в плоскости хОу; поэтому . Отсюда следует, что пространственная система параллельных сил никогда не приводится к динаме, а приводится к равнодействующей, если , или к паре, если 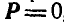, или взаимно уравновешивается, если .

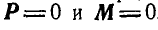В последнем случае мы будем иметь три уравнения равновесия:

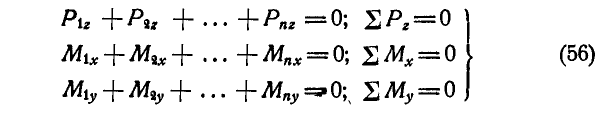
Сложение параллельных сил можно произвести иначе. Пусть на тело (рис. 124) действуют 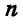параллельных сил.

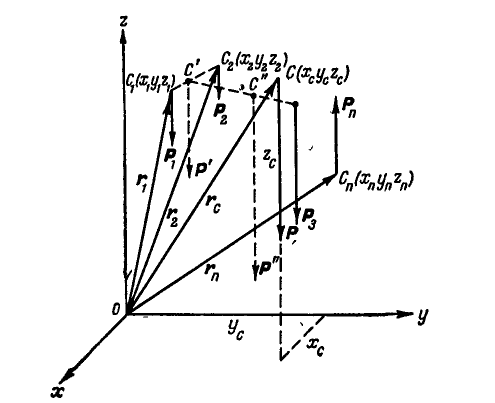
Рис. 124.

Складывая сначала силы 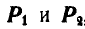находим их равнодействующую 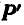; далее полученную равнодействующую 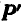складываем с силой 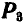и получаем их равнодействующую 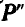, которую складываем со следующей силой 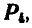, и т. д. Произведя последовательное сложение всех параллельных сил, получим их общую равнодействующую:

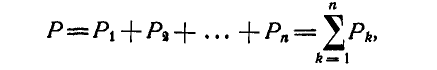
которая имеет определенную линию действия.

Если повернем все силы 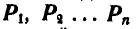на один и тот же угол, то найдем для них новую равнодействующую, по величине равную первой, но имеющую другую линию действия. Точка пересечения линий действия равнодействующих называется центром параллельных сил.

Следовательно, центром параллельных сил называется та точка С приложения их равнодействующей, которая не меняет своего положения при повороте всех сил на один и тот же угол.

Если известны координаты точек приложения составляющих сил, то координаты центра параллельных сил найдутся по формулам, аналогичным формуле (54), выражающим равенство моментов равнодействующей и составляющих относительно координатных осей, т. е.:

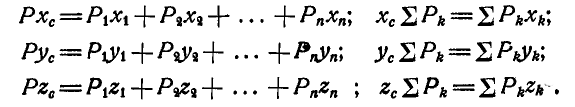
Для получения последнего равенства следует все силы повернуть на 90" параллельно оси Ох или Оу.

Координаты центра параллельных сил будут:

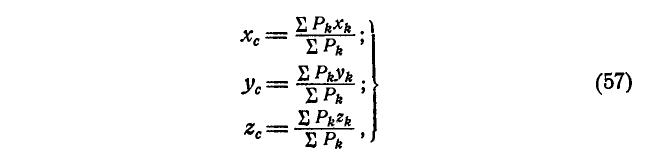
или в векторной форме

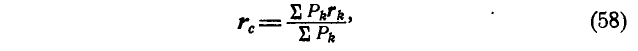
где 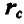— радиус-вектор, определяющий положение центра параллельных сил;

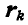— радиус-вектор 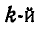точки.

Центр тяжести

На каждую 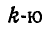частицу твердого тела, находящегося вблизи земной поверхности, действует сила тяжести 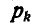, направленная вертикально вниз. Считая, что силы тяжести всех частиц тела параллельны между собой, найдем координаты центра всех параллельных сил тяжести, который называется центром тяжести тела и определяется по формуле (58):

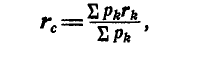
где 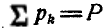называется весом тела.

Если тело однородное, то отношение веса 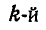частицы к ее объему 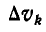постоянно, т.е.:

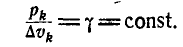
Заменяя в равенстве (58) 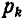через 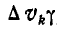, имеем:

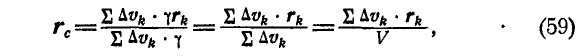
или

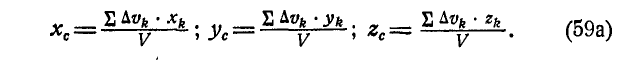
Формулы (59) и (59a) определяют координаты центра тяжести объема.

Выражения 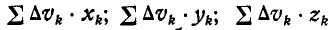называются статическими моментами объема относительно плоскостей yOz, xOz и хОу.

Рассуждая аналогично, можно найти также координаты центра тяжести площади:

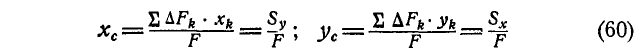
и линии:

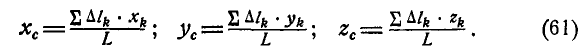
В последних равенствах F—величина всей площади, L — длина всей линии, а V—величина объема. Величины 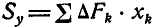и 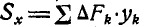  называются статическими моментами плоской фигуры относительно осей у и х.

Из равенства (60) следует, что если известно положение центра тяжести плоской фигуры, то ее статические моменты относительно осей могут быть найдены также по формулам:

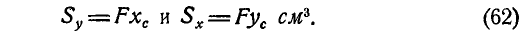
Статический момент плоской фигуры относительно оси х или у может быть величиной положительной, отрицательной и равной нулю, если ось проходит через центр тяжести фигуры. В самом деле из равенств (60) следует, что если 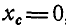, то 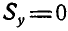и ; при ; .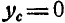

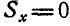При нахождении центра тяжести плоской фигуры вместо равенства (60) иногда применяют графический способ, основанный на построении двух веревочных многоугольников. Пусть, например, требуется определить положение центра тяжести фигуры, показанной на рисунке 125. Для этого разбиваем всю фигуру на такие площади, положение центров тяжести которых нам известно (в данном примере на три прямоугольника).

Приложим в центрах тяжести 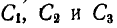этих площадей вертикальные силы 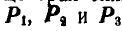, пропорциональные площадям 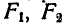и 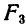. Построив затем веревочный многоугольник, находим на чертеже положение линии действия равнодействующей сил .

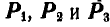Так как положение центра параллельных сил, а также центра тяжести не изменяется при повороте всех сил на один и тот же угол, то, повернув все силы 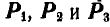вокруг 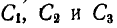например, на 90°, вновь строим веревочный многоугольник и находим положение линии действия равнодействующей для повернутых сил.

Пересечение линий действия равнодействующих, найденных для двух случаев, и определит положение точки С —центра тяжести всей фигуры.

При построении веревочного многоугольника для сил, повернутых на 90°, можно было бы, не строя многоугольника сил,

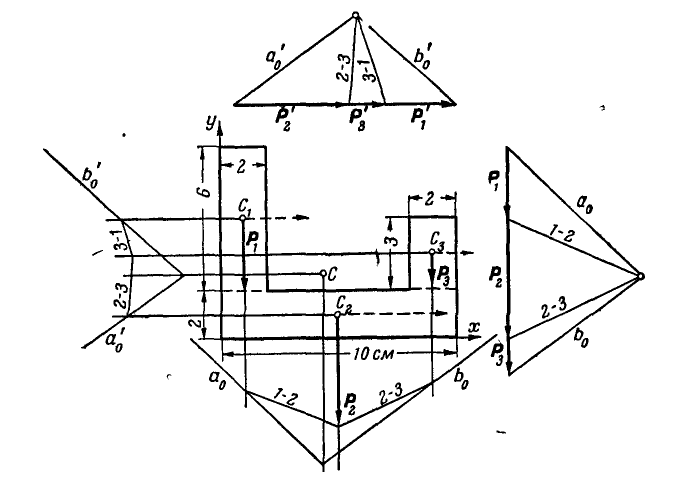
Рис. 125.

построить веревочный многоугольник, стороны которого были бы перпендикулярны соответствующим сторонам имеющегося веревочного многоугольника.

При заданных размерах фигуры (рис. 125) положение точки С можно определить также аналитически. Для этого, разбив фигуру, как и при графическом построении, на три прямоугольника и выбрав координатные оси, перепишем равенства (60) в следующем виде:

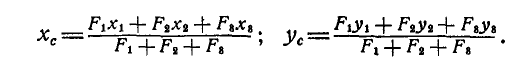
После подстановки численных значений будем иметь:

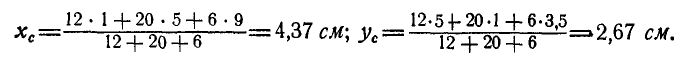
В некоторых случаях при определении положения центра тяжести плоской фигуры или плоской кривой удобно бывает одно из равенств (60) или (61) представить в иной форме, которая была предложена Паппом.

Пусть требуется, например, определить величину 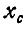для фигуры, показанной на рисунке 126.

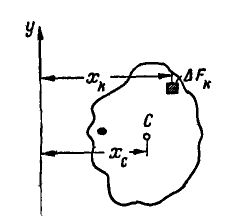
Рис. 126. 

Будем вращать контур этой фигуры вокруг оси у, тогда мы получим некоторую замкнутую поверхность. Тело, ограниченное такой поверхностью, называется телом вращения.

Для определения объема тела вращения, разобьем всю площадь F фигуры на элементарные площадки .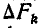

При вращении фигуры вокруг оси у каждая элементарная площадка 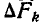опишет элементарное круговое кольцо, объем которого равен .

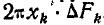Следовательно, объем тела вращения определится по формуле:

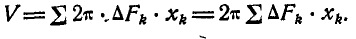
Но так как на основании первого равенства (60) 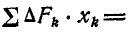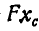, то окончательно получим:

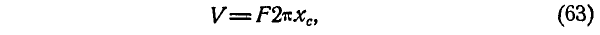
т. е. объем тела, полученного вращением плоской фигуры вокруг оси, расположенной в плоскости этой фигуры, равен произведению площади этой фигуры на длину окружности, описанной ее центром тяжести.

В этом заключается первая теория Паппа.

В качестве примера определим положение центра тяжести площади половины круга радиуса R (рис. 127).

Будем вращать эту площадь вокруг оси у, совпадающей с диаметром, тогда тело вращения будет представлять шар, объем которого равен 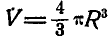. Площадь плоской фигуры равна половине площади круга, т. е. .

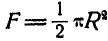Подставляя значения V и F в равенство (63), будем иметь:

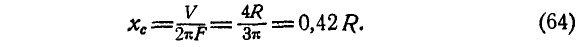
Аналогично можно иногда найти и положение центра тяжести плоской кривой. Пусть центр тяжести С плоской кривой (рис. 128) находится от оси у на расстоянии .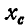

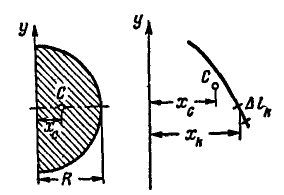
Рис. 127.             Рис. 128.     

Будем вращать эту кривую вокруг оси у, тогда мы получим некоторую поверхность вращения, величину площади которой обозначим через F. Для определения площади F разобьем кривую на элементарные участки .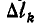

При вращении кривой вокруг оси у каждый элемент 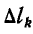опишет элементарную кольцеобразную поверхность, площадь которой равна: 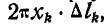а площадь всей поверхности вращения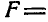

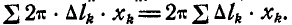
С другой стороны, из первого равенства (61) следует, что 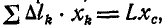, поэтому 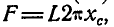т. е. площадь поверхности, полученной вращением плоской кривой вокруг оси,расположенной в плоскости этой кривой, равна произведению длины этой кривой на длину окружности, описанной ее центром тяжести. В этом заключается вторая теорема Паппа.

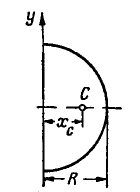
Рис. 129.

Применим эту теорему для определения центра тяжести дуги полуокружности радиуса R (рис. 129). Будем вращать эту дугу вокруг оси у, совпадающей с диаметром, тогда поверхность вращения, представляющая поверхность шара, будет 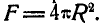Длина плоской кривой 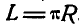. Подставляя значения F и L в равенство 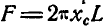, получим:

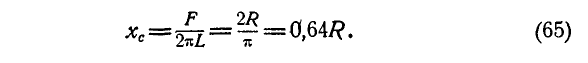
Правила нахождения центра тяжести

При нахождении центров тяжести тел следует помнить следующие правила:

1. Если тело имеет плоскость симметрии, то центр тяжести его находится в этой плоскости.
2. Если тело имеет две плоскости симметрии, то его центр тяжести находится на линии пересечения этих плоскостей.
3. Если тело имеет три плоскости симметрии, то его центр тяжести находится в точке пересечения этих плоскостей.
4. Если тело можно разбить на такие части 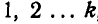, положения центров тяжести которых нам известно, то координаты центра тяжести тела найдутся по формулам (57), (59), (60), (61).

Чтобы получить вполне точные формулы для определения координат центра тяжести в упомянутых случаях, мы должны перейти к пределу в предположении, что число элементов неограниченно возрастает при стремлении величины каждого элемента к нулю.

При решении многих задач полезно пользоваться справочной таблицей положений центров тяжести.

Задача №1

Определить положение центра тяжести тела, состоящего из однородных стержней (рис. 130). Размеры указаны в сантиметрах.

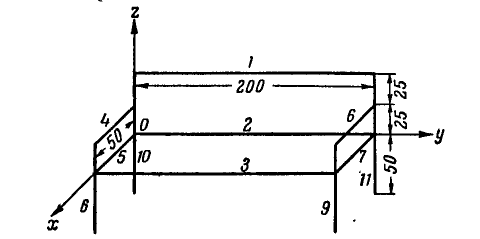
Рис. 130.

Решение. Обозначим стержни, из которых состоит тело, через 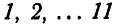, их длины через 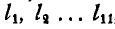, а координаты центра тяжести каждого стержня через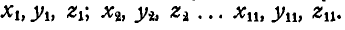

Тогда координаты центра тяжести всего тела 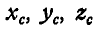по формуле (61) будут: 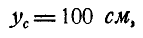так как тело имеет плоскость симметрии, параллельную плоскости zOx,

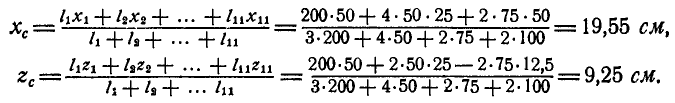
Задача №2

Найти координаты центра тяжести однородной пластинки (рис. 134). Размеры указаны в сантиметрах.

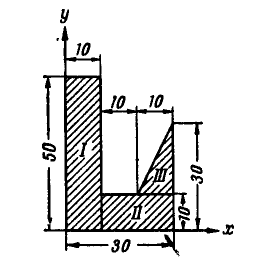
Рис. 134.

Решение. Разобьем площадь пластинки на три площади (два прямоугольника и

один треугольник), положения центров тяжести которых нам известны.

Обозначив эти площади соответственно через 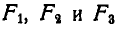, на основании равенств (60) получим:

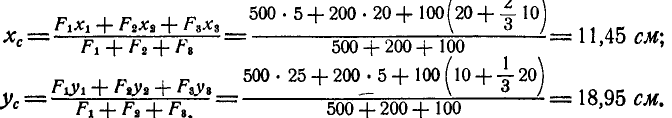
Задача №3

В нижнюю часть прямоугольника вписана окружность (рис. 135). Найти статические моменты заштрихованной площади относительно осей х и у.

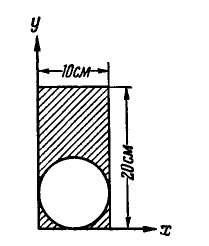
Рис. 134.

Решение. Искомые статические моменты определятся по формулам (62) путем вычитания из статического момента площади прямоугольника статического момента площади круга:

 

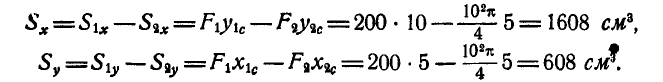
Задача №4

Определить координаты центра тяжести однородного тела, все ребра которого параллельны соответствующим координатным осям (рис. 136). Размеры на чертеже проставлены в сантиметрах.

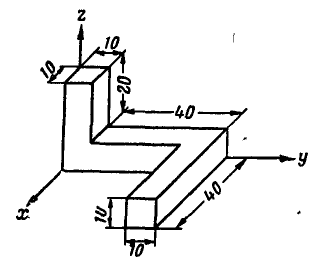
Рис. 136.

Указание: разбиваем все тело каким-либо способом на три прямоугольных параллелепипеда, положения центров тяжести которых нам известны, и по формулам (59а) определяем координаты центра тяжести тела.

Ответ: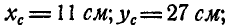  

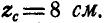
Задача №5

Найти положение центра тяжести дуги окружности, радиус которой R, длина 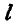 и хорда .

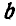Решение. Проведем ось 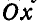через центр дуги и середину ее хорды; тогда центр тяжести дуги будет находиться на оси 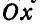, которая является ее осью симметрии.

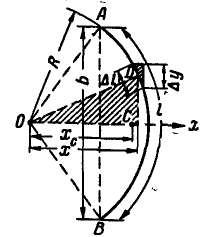
Рис. 137.

Разобьем дугу на бесконечное множество элементов 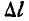и обозначим абсциссу середины каждого элемента через х. Тогда абсцисса центра тяжести всей дуги может быть найдена по первой формуле (61):

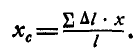
Из подобия заштрихованных ков (рис. 137) находим: 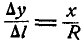, или 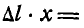 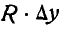 и, следовательно: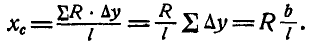 

Задача №6

Найти координаты центра тяжести заштрихованной фигуры, контур которой ограничен полуокружностями диаметром 20 см и 10 см (рис. 138). 

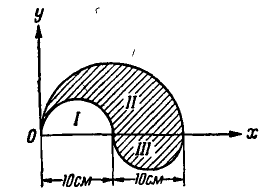
Рис. 138.

Решение. Будем считать, что заданная фигура состоит из трех частей I, II  и III, из которых площади I и III ограничены осью 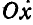и полуокружностями диаметром 10 см, а площадь II ограничена той же осью и полуокружностью диаметром 20 см. Так как на самом деле площади I не существует, то ее следует брать со знаком минус.

Обозначая площадь I, II и III  через 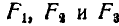, координаты их центров тяжести через 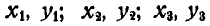и пользуясь равенством (64), имеем:

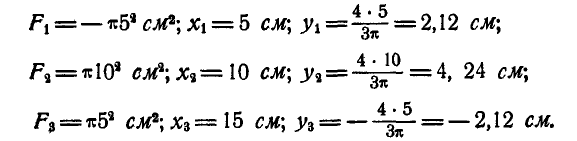
Применяя формулы (60), получим:

• Заказать решение задач по теоретической механике

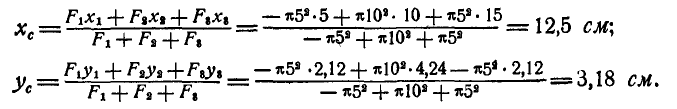
Координаты центра параллельных сил

Центром параллельных сил называют точку на линии действия равнодействующей системы параллельных сил, вокруг которой поворачивается эта линия действия, если все силы поворачиваются вокруг точек их приложения, оставаясь параллельными между собой

Центр параллельных сил. Система параллельных сил, приложенных к твердому телу и направленных в одну сторону, не может находиться в равновесии или приводиться к паре сил—такая система приводится к равнодействующей. Пусть параллельные силы 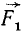, , 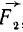, 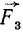. . ., 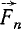(рис. 70), составляющие данную систему, не лежат в одной плоскости.

Для получения равнодействующей применим метод последовательного сложения. Сначала сложим две силы 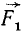и 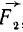по известному правилу сложения двух параллельных сил. Равнодействующую этих сил обозначим 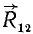и приложим в точке C₁₂, находящейся на прямой, соединяющей точки приложения А и В слагаемых сил, и определяемой из пропорции

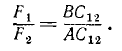     (11)

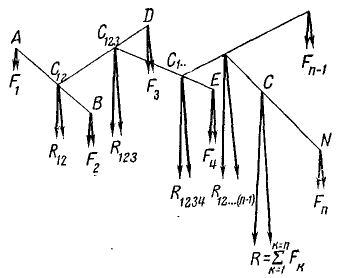
Рис. 70

Затем проведем плоскость через линии действия сил 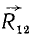и 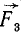 и найдем равнодействующую трех сил R123, которую мы приложим, руководствуясь тем же правилом, в точке 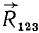. Поступая далее таким же образом, мы найдем равнодействующую всей системы 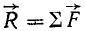и точку C ее приложения.

Предположим, что все параллельные силы повернулись в какую-либо сторону на некоторый угол. Очевидно, что тогда и равнодействующая 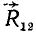двух первых сил повернется в ту же сторону и на тот же угол, так как равнодействующая параллельных сил параллельна своим составляющим. Точка C₁₂ останется на прежнем месте, так как модули сил F₁ и F₂ и их точки приложения А и В не изменились, а следовательно, не изменилась и пропорция (11). Не изменится также и модуль равнодействующей, равный, как известно, сумме модулей составляющих сил. Но если величина и точка приложения силы 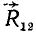не изменились, а сила повернулась, став параллельной 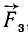, то, следовательно, не изменится и точка приложения равнодействующей 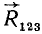трех сил системы. Рассуждая таким образом и дальше, мы убедимся, что и точка C останется на прежнем месте, а линия действия равнодействующей  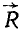повернется вокруг этой точки, оставаясь параллельной линиям действия сил системы.

Точка приложения равнодействующей не является строго фиксированной, так как равнодействующую всегда можно перенести в другую точку ее линии действия, поэтому мы определим центр параллельных сил как точку на прямой действия равнодействующей системы параллельных сил, вокруг которой поворачивается эта прямая, если все параллельные силы поворачиваются вокруг точек их приложения, оставаясь параллельными между собой.

Центром тяжести твердого тела называют центр параллельных сил, представляющих веса материальных частиц твердого тела

Центр тяжести и его координаты

Примером центра параллельных сил может явиться центр подъемных сил корабля или центр давления насыпи на плоскую стенку. Но особенно часто приходится определять центр параллельных сил тяжести, которые, по сути дела, не являются параллельными, но могут с большой точностью быть приняты за параллельные. Под действием силы тяжести каждая материальная частица тела, находящаяся вблизи Земли, притягивается к Земле и вектор силы тяжести направлен «вниз» по отвесу к центру Земли. Таким образом, силы тяжести двух частиц не являются параллельными, так как их линии действия пересекаются в центре Земли. Однако громадные размеры Земли и сравнительно небольшие размеры материальных тел, центры тяжести которых приходится определять, позволяют считать силы тяжести частиц одного тела параллельными. Например, направления сил тяжести двух частиц, находящихся на корме и на носу океанского лайнера длиной 300 м, составляют между собой угол в десять секунд дуги, который невозможно даже отметить на чертеже ввиду его малости. C очень большой точностью можно принимать силы тяжести различных частиц одного и того же тела за параллельные, а общий вес тела считать приложенным в центре этих параллельных сил тяжести, называемом центром тяжести тела.

Как бы ни поворачивали тело и ни изменяли его положение по отношению к Земле, силы тяжести его отдельных частиц останутся вертикальными и параллельными между собой. Относительно тела они будут поворачиваться вокруг своих точек приложения, сохраняя величину и параллельность. При этом линия действия равнодействующей параллельных сил будет проходить через одну и ту же точку— центр тяжести. Отсюда следует, что центр тяжести твердого тела не изменяет своего положения относительно этого тела при изменении положения самого тела. Положение центра тяжести в теле зависит только от формы тела и от распределения в нем материальных частиц.

Координаты центра тяжести определяются равенствами

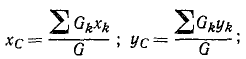
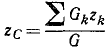
Отыскивать центр тяжести какого-либо тела методом последовательного сложения векторов сил тяжести его частиц не представляется целесообразным из-за громоздкости вычислений. Мы выведем общие формулы, позволяющие сравнительно легко определять координаты центра параллельных сил (или центра тяжести тела).

Разобьем мысленно тело на такие части, центры тяжести которых можно было бы сравнительно легко определить. Заменим каждую такую часть точкой (которую мы будем называть изображающей точкой), совпадающей с центром тяжести этой части и имеющей вес, равный весу этой части тела. Таким образом, изображающая точка характеризуется своим весом и положением в исследуемом теле, а все твердое тело заменено нами системой изображающих точек. Положим, что изображающих точек в теле получилось п. Веса этих точек будем обозначать буквой G с индексом, указывающим принадлежность к той или иной точке: G_l, G₂, G₃, .... G_n. Построим систему координат, неразрывно связанную с данным телом, направив ось Oz по вертикали вверх (рис. 71, а), и обозначим координаты изображающих точек через х, у и z с индексами, соответствующими точкам. Равнодействующая всех сил тяжести системы изображающих точек равна весу G всего тела, приложенному в его центре тяжести, координаты которого обозначим x_c, у_с и z_c.

Mx=yZ — zY, My = zX—xZ, Mz = xY — yX.     (23)

Выразим по первой из этих формул моменты относительно оси х сил тяжести всех частей тела, т. е. сил, приложенных к изображающим точкам. Проекции этих сил на ось у равны нулю, а на ось z — весам соответствующих частей тела с отрицательным знаком:

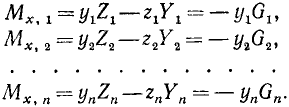
Сложив отдельно левые и правые части этих равенств, получим

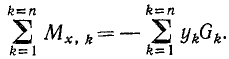
Выразим теперь по той же формуле (23) момент равнодействующей относительно оси Ох:

M_x(G) = -y_cG.

В левой части этого равенства записан момент равнодействующей G относительно оси х, а в левой части предыдущего равенства—сумма моментов всех составляющих относительно той же оси. Эти две величины равны ,между собой, следовательно, равны и правые части равенства, т. е.

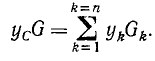
Из этого соотношения находим ординату центра тяжести:

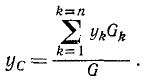
Если воспользоваться вторым из равенств (23)

My = zХ—xZ

и определить сумму моментов сил тяжести, приложенных к изображающим точкам, относительно оси у, приравняв ее моменту равнодействующей относительно той же оси, то аналогично предыдущему получим абсциссу центра тяжести

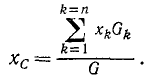
Для определения аппликаты z_c центра тяжести тела повернем это тело вместе с осями координат на 90° вокруг оси х в направлении вращения стрелок часов, тогда место оси у займет ось z, а ось у будет направлена по вертикали вниз. В результате этого поворота все силы тяжести повернутся на один и тот же угол 90°, а центр параллельных сил (или в нашем случае—центр тяжести тела) не изменит своего местоположения как относительно тела, так и относительно неразрывно связанных с ним координатных осей (рис. 71,б).

Силы тяжести расположатся теперь параллельно оси у, и их проекции Y на эту ось будут положительны и равны модулям сил тяжести. Найдем моменты сил тяжести относительно оси х при новом положении тела:

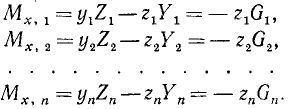
Суммируя отдельно левые и правые части этих равенств, найдем

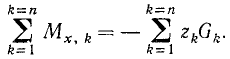
Определив момент равнодействующей относительно той же оси, получим

М_x(G) = -Z_cG

и, приравнивая момент равнодействующей сумме моментов составляющих, найдем аппликату центра тяжести:

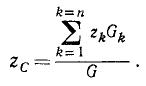
Напишем теперь вместе выведенные нами формулы:

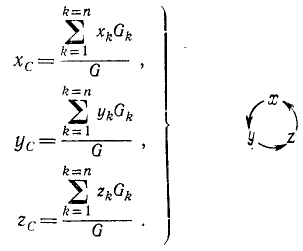
Эти формулы определяют положение центра тяжести.

Суммы произведений сил на координаты точек их приложения, стоящие в числителях этих формул, называют статическими моментами, а в знаменателях всех формул мы имеем вес всего тела.

Координаты х, у и z всякой точки равны проекциям на оси координат радиуса-вектора 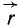точки относительно начала координат. Следовательно, три аналитических равенства (45) можно заменить одним векторным равенством

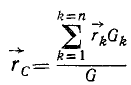
Центр тяжести линий, плоских фигур и тел

Если тело имеет плоскость симметрии (или ось симметрии, или центр симметрии), то центр тяжести тела лежит на этой плоскости (оси или в центре) симметрии

Если тело однородное, то, представляя, вес тела как произведение его объема V на вес γ единицы объема, а вес  γ отдельных его частей — как произведение γ на их объем, получим:
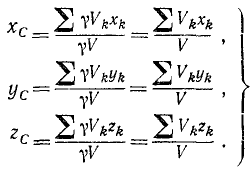          (46)

В таком смысле можно говорить о центре тяжести объема, понимая под этим центр тяжести однородного тела данной геометрической формы.

В том же смысле говорят о центре тяжести поверхностей и фигур, понимая под этим центр тяжести однородных пластин равной толщины. Его можно определить по аналогичным формулам:

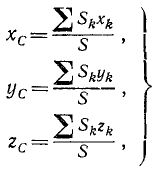          (47)

где S_k (при k=1, 2, 3, .... n) — площади отдельных частей пластины, S—площадь всей пластины.

В том же смысле говорят и о центре тяжести линий, понимая под линией тонкую однородную нить:
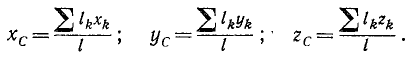          (48)
Если тело, хотя бы и неоднородное, имеет плоскость симметрии, т. е. каждой частице тела по одну сторону этой плоскости соответствует симметрично расположенная частица такого же веса по другую сторону плоскости, то центр тяжести такого тела лежит на плоскости симметрии. В самом деле, если каждой частице по одну сторону плоскости соответствует такая же по весу и симметрично расположенная частица по другую сторону, то равнодействующая сила тяжести этих двух частиц приложена к точке, лежащей в плоскости симметрии. По той же причине в плоскости симметрии лежат, и точки приложения равнодействующих весов других взятых попарно симметричных частиц. Складывая эти равнодействующие, найдем и их равнодействующую, которая приложена в той же плоскости, а точка приложения этой равнодействующей лежит в центре тяжести тела.

Для случая, если тело имеет ось симметрии или центр симметрии, можно доказать аналогичные теоремы. Из этих теорем можно вывести следующие следствия:

1. центр тяжести однородного прямого стержня (или отрезка прямой) лежит в его середине;
2. центр тяжести параллелограмма (однородной тонкой пластины, имеющей форму параллелограмма) лежит в точке пересечения его диагоналей, являющейся центром симметрии параллелограмма;
3. центры тяжести однородного правильного многоугольника, круга, эллипса, шара лежат в их геометрических центрах.

В виде примеров ограничимся определением центров тяжести дуги окружности и площади треугольника, так как учащиеся будут иметь возможность и даже необходимость определять центры тяжести различных тел на упражнениях по интегральному исчислению. Построим оси координат, как показано на чертеже (рис. 72), и разобьем дугу на n элементарных отрезков Δl_k. Центр тяжести дуги лежит на оси симметрии (y_c= 0). Абсциссу центра тяжести найдем по (48):

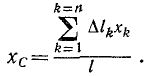
Приняв элементарные отрезки дуги за прямолинейные, разложим один из них на Δx_k и Δy_k. Если радиус, проведенный на середину этого отрезка, составляет с осью Ox угол a_k, то, как видно из чертежа,

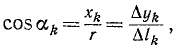
откуда 

x_kΔl_k= r∆y_k.

Составим такие выражения для всех отрезков и просуммируем их:

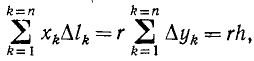
где h—длина хорды. Подставив найденное выражение в (48), определим центр тяжести дуги.

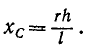
Учитывая, что h = 2r sin α и l = 2ar, этой формуле можно дать следующий вид:

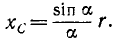
В частности, для полуокружности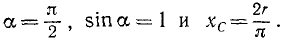 

Центр тяжести треугольника лежит на пересечении его медиан на расстоянии от основания, равном одной трети высоты

Разобьем площадь треугольника (рис. 73) прямыми, параллельными основанию, на очень большое число узких полосок, которые можно рассматривать как отрезки прямых линий. Центр тяжести каждого отрезка лежит на его середине, а потому и центр тяжести всей площади треугольника лежит где-то на медиане, соединяющей вершину треугольника с серединой его основания. Разбив площадь треугольника прямыми, параллельными какой-либо другой стороне, и рассуждая аналогично, мы придем к заключению, что центр тяжести треугольника должен лежать и на другой медиане. Следовательно, центр тяжести площади треугольника лежит в точке пересечения его медиан. Как известно из планиметрии, медианы пересекаются на расстоянии одной трети от основания и двух третей от вершины.

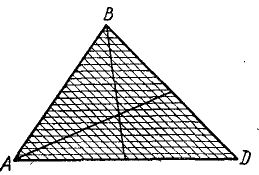
Рис. 73

Для определения координат центра тяжести тел и фигур сложной формы эти тела и фигуры заменяют системой точек и определяют координаты по формулам (45)

Для нахождения координат центра тяжести тела (или фигуры), имеющего сложную форму, нужно мысленно разбить это тело (или эту фигуру) на такие простейшие формы (если, конечно, это возможно), для которых положение центра тяжести и вес могут быть легко определены. В центре тяжести каждой такой части тела считают приложенным вес этой  части. Будем называть, как мы это уже сделали выше, центры тяжести частей с приложенными в них весами этих частей изображающими точками. Для нахождения координат центра тяжести тела сложной формы остается лишь найти центр тяжести всех изображающих точек по формулам (45). Однако на практике эти подсчеты содержат большие трудности. Так, например, некоторые тела (пароходы, самолеты, автомобили и т. п.) приходится иногда заменять тысячами изображающих точек. В этих случаях может оказаться удобным подсчет по таблице, приведенной нами при решении следующей задачи.

Задача №7

Определить координаты центра тяжести контура прямоугольного параллелепипеда (рис. 74), ребра которого суть однородные бруски длиной: OA =8 дм; ОВ = 4 дм; OC = 6 дм; веса брусков, выраженные в ньютонах: OA =250; OB, ОС и CD по 75; CG = 200, AF= 125; AG и GE — по 50; BD, BF, DE и EF — по 25.

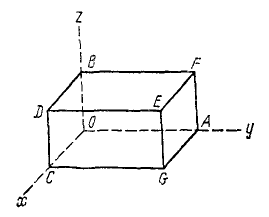
Рис. 74

Решение. Заменим стержни изображающими точками. Каждая из них имеет координаты середины того стержня который она изображает, и его вес.

Заполняем таблицу:

№ п.п.	Название	Gk	xk	yk	zk	Gkxk	Gkyk	Gkzk
1 2 3 4 5 6 7 8 9 10 11 12	OB OC CD BD BF OA CG DE AG AF EG EF	75 75 75 25 25 250 200 25 50 125 50 25	0 3 6 3 0 0 6 6 3 0 6 3	0 0 0 0 4 4 4 4 8 8 8 8	2 0 2 4 4 0 0 4 0 2 2 4	0 225 450 75 0 0 1200 150 150 0 300 75	0 0 0 0 100 1000 800 100 400 1000 400 200	150 0 150 100 100 0 0 100 0 250 100 100
		1000				2625	4000	1050

Суммируя третий столбец и подсчитав суммы трех последних, определяем вес системы и статические моменты, и нам остается лишь поделить статические моменты на вес системы.

Ответ. x_c=2,625 дм; y_c = 4,000 дм; z_c= 1,050 дм.

Если в теле или фигуре имеются полости или отверстия, то для определения центра тяжести пользуются теми же приемами и формулами, считая при этом объемы и площади вырезанных частей отрицательными. Этот метод иногда называют методом отрицательных масс.

Поясним применение этого метода решением задачи.

Задача №8

В диске радиуса r сделан эксцентрический вырез в виде круга, построенного на Радиусе как на диаметре. Найти центр тяжести оставшейся части диска (рис. 75).

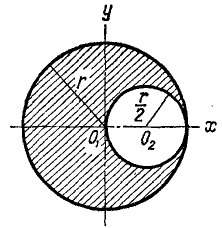
Рис. 75

Решение. Оставшаяся часть диска имеет ось симметрии. Начало координат возьмем в центре диска и ось симметрии примем за ось Ох. Искомый центр тяжести лежит на оси симметрии, следовательно, у_c = 0. Найдем абсциссу центра тяжести. Для решения задачи воспользуемся методом отрицательных масс и представим оставшуюся часть диска двумя изображающими точками. Первая — это точка, лежащая в центре диска и имеющая массу, равную массе диска (считаем, что вырез в диске не сделан). Так как диск однородный, то за массу диска можно принять его площадь. Следовательно,

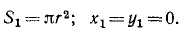
Вторая точка — это точка, лежащая в центре выреза, имеющая массу, равную массе вырезанной части диска, но взятую с обратным знаком. Опять вместо массы вырезанной части возьмем площадь. Имеем

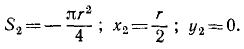
От присоединения этой «отрицательной площади» к площади первого диска и получается фигура, изображенная на рис. 75.

Абсциссу центра тяжести оставшейся части диска находим по формуле

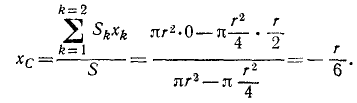
Ответ.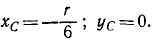  

Объем тела, полученного от вращения плоской фигуры вокруг оси, лежащей в ее плоскости, равен произведению площади фигуры на длину дуги, описанной ее центром тяжести

Теоремы Паппы

При определении центров тяжести часто оказываются полезными две следующие теоремы. Пусть даны какая-либо плоская фигура, ее центр тяжести C (рис. 76) и ось zz, не пересекающая фигуры, но лежащая в ее плоскости. Разобьем площадь S фигуры на n элементарных частей ΔS_k. Поворачивая фигуру вокруг оси zz, получим тело вращения, которое можно представить как состоящее из элементарных колец, объемом 2πx_kΔS_k каждое.

Тогда объем тела

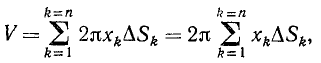
но 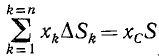 —статический момент площади, а потому

V=2πx_CΔS       (49)

Если объем тела и площадь образующей фигуры известны, то по (49) легко найти положение центра тяжести фигуры.

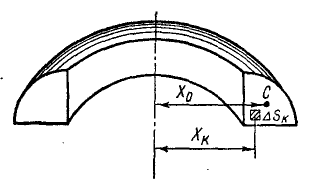
Рис. 76

Задача №9

Найти центр тяжести площади полуокружности. 
Решение. Объем шара 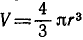, площадь полукруга 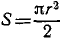, подставляя в (49), получаем

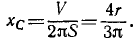
Ответ. х_c = 0,4244r.

Легко доказать аналогично и вторую теорему: площадь поверхности, описанной при вращении плоской кривой вокруг оси, лежащей в ее плоскости, но не пересекающей эту кривую, равна произведению длины кривой на длину траектории, описанной ее центром тяжести.

S = 2πx_Cl.    (50)

Задача №10

Найти центр тяжести дуги полуокружности.

Решение. Поверхность шара S = 4πr², длина полуокружности l= πr. Подставляя в (50), получаем уже известный нам результат

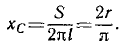
Ответ. х_с = 0,6366r.