
Тригонометрические функции произвольного угла с примерами решения
Содержание:
Тригонометрические функции произвольного угла
Угол поворота
До недавнего времени говоря об угле мы имели в виду угол, полученный между двумя неподвижными сторонами. Угол также можно рассматривать как измерение поворота. Например, радиус колеса, расположенного по горизонтали при вращении вокруг неподвижной оси, через определённое время относительно начального положения образует некоторый угол. К тому же значение угла зависит от направления поворота. Любой угол можно рассматривать как фигуру, полученную вращением луча вокруг начальной точки.
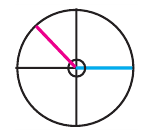
Начальное положение луча соответствует одной стороне угла, конечное положение - другой стороне. При вращении луча на координатной плоскости относительно начала координат в направлении по часовой стрелке или против часовой стрелки, можно получить различные углы.
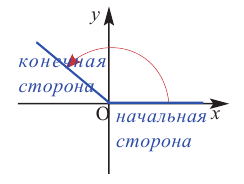
Начальная сторона угла поворота совпадает с положительным направлением оси абсцисс. Сторону, полученную при вращении относительно начала координат (вершины угла), назовём конечной стороной. Принято считать, что если поворот происходит в направлении против часовой стрелки, то угол имеет положительное значение, при повороте в направлении по часовой стрелке, угол имеет отрицательное значение,
положительный угол отрицательный угол 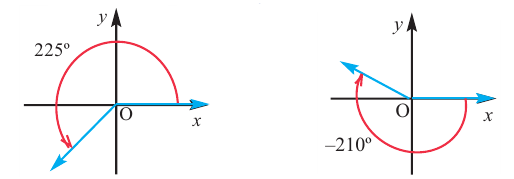
Координатные оси разбивают координатную плоскость на 4 четверти. Значение угла, в зависимости от того, в какой четверти расположена его конечная сторона, меняется в определенном интервале.
Конечная сторона угла может совершить один или несколько оборотов относительно начала координат. Один полный оборот соответствует углу 360°. Существует бесконечное число углов поворота, у которых начальная и конечная стороны совпадают. Например, конечные стороны углов 30°и 390° совпадают. В общем, для углов поворота 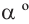 и
и 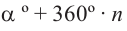 (здесь
(здесь 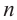 произвольное целое число) конечные стороны совпадают.
произвольное целое число) конечные стороны совпадают.
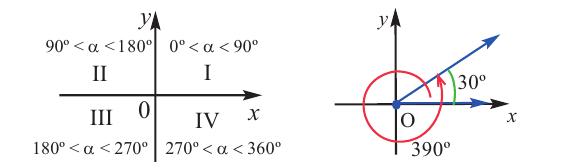
Радианная и градусная мера угла
Пример 1. Нарисуйте угол заданной величины. Определите какой четверти принадлежит конечная сторона угла. 
Пример 2. На координатной плоскости покажите и запишите градусные меры двух положительных и одного отрицательного угла поворота, конечные стороны которых совпадают с конечной стороной угла 60°. 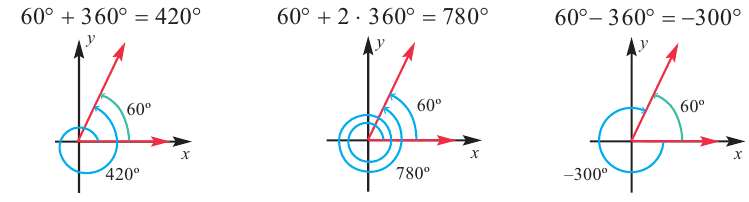
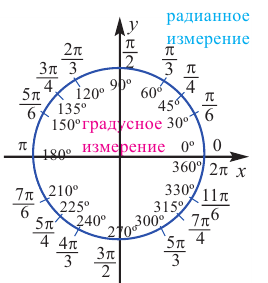
Радианное измерение углов
Угол в один радиан-это центральный угол, у которого длина дуги равна радиусу. Радианная мера угла есть отношение длины соответствующей дуги к радиусу окружности: 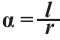 . Величина угла, выраженная в радианах не зависит от длины радиуса (объясните, воспользуясь подобием фигур на рисунке).
. Величина угла, выраженная в радианах не зависит от длины радиуса (объясните, воспользуясь подобием фигур на рисунке).
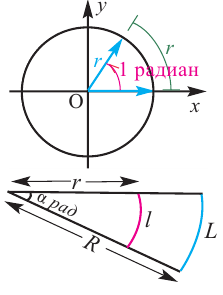
Пример 1. Сколько радиан составляет центральный угол, длина дуги которого равна 12 см, если радиус окружности равен 4 см?
Решение: 1 радиан соответствует длине дуги 4 см. Дуге длиной 12 см будет соответствовать угол 12 : 4 = 3 радиан. Длина окружности 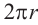 . Если центральный угол, соответствующий дуге окружности радиуса
. Если центральный угол, соответствующий дуге окружности радиуса 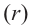 равен 1 радиану, то дуге, равной
равен 1 радиану, то дуге, равной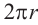 ; соответствует центральный угол
; соответствует центральный угол 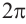 . Ниже показаны радианные меры углов поворота.
. Ниже показаны радианные меры углов поворота.
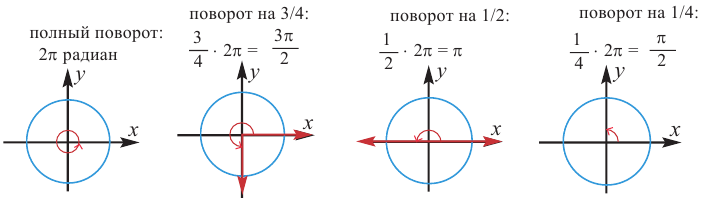
Радианная мера одного целого оборота равна 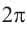 , градусная мера 360°. То есть,
, градусная мера 360°. То есть, 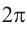 радиан = 360°. Отсюда можно установить следующую связь между радианной и градусной мерой. Преобразование радиан в градусы:
радиан = 360°. Отсюда можно установить следующую связь между радианной и градусной мерой. Преобразование радиан в градусы:
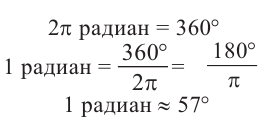
Преобразование градусов в радианы:
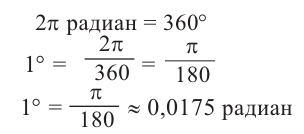
Таким образом, 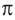 рад = 180°. Обозначение "рад' часто опускают. Вместо
рад = 180°. Обозначение "рад' часто опускают. Вместо 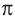 рад = 180° обычно пишут
рад = 180° обычно пишут 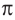 = 180°. Отсюда получаем, что
= 180°. Отсюда получаем, что
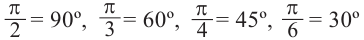
Используя соответствующие радианные и градусные меры углов, расположенных в первой четверти, можно найти увеличенные в разы значения других углов. Например, если 30° =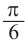 , тогда 150° =
, тогда 150° =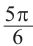
Пример 2. Выразите углы, заданные в градусах радианами, а углы, заданные радианами в градусах, а) 60° ; б)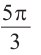
Решение.
а)60° =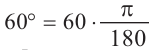 радиан
радиан 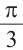 — радиан
— радиан  1,047 радиан
1,047 радиан
б)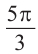
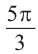 радиан
радиан 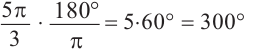
Пример 3. Выразите углы, конечная сторона которых совпадает с углом 45°, в градусах и радианах.
Решение: Конечная сторона угла 45°совпадает с углами 405° и 315°, а также существует бесконечно много углов, конечные стороны которых совпадают с конечной стороной угла 45°: 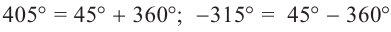 ;
;
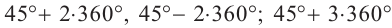 ,
,
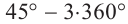 или
или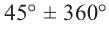 ,
,
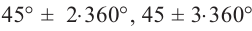 .
.
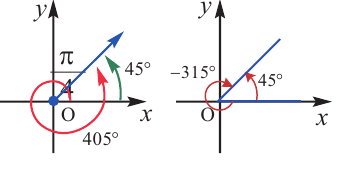
В радианах это можно записать как
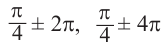 и т.д. Все углы, конечные стороны которых совпадают с углом
и т.д. Все углы, конечные стороны которых совпадают с углом 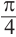 в общем виде записываются так:
в общем виде записываются так: 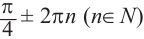
Пример, а) 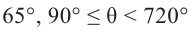
Все углы поворота, конечные стороны которых совпадают с углом 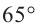
можно найти но формуле 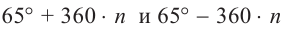 .
.

Как видно, в заданном интервале, расположен всего один угол 425°. Пример. д)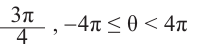 Все углы поворота, конечные стороны которых, совпадают с этим углом можно найти по формуле
Все углы поворота, конечные стороны которых, совпадают с этим углом можно найти по формуле 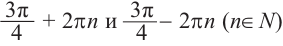 .
. 
Интервалу 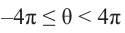 принадлежат углы
принадлежат углы 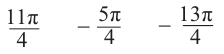
Длина дуги
Запишем формулу нахождения длины дуги, соответствующей центральному углу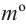 окружности радиуса
окружности радиуса 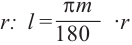 . Используя радианную меру длину окружности можно найти ещё проще. По определению радиана, если
. Используя радианную меру длину окружности можно найти ещё проще. По определению радиана, если 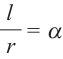 , тогда длина дуги равна произведению радиуса и радианной меры угла:
, тогда длина дуги равна произведению радиуса и радианной меры угла: 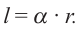 Длина дуги окружности находится с радиусом в прямо пропорциональной зависимости.
Длина дуги окружности находится с радиусом в прямо пропорциональной зависимости.
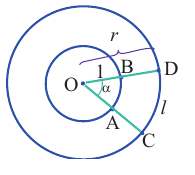
Площадь сектора
Центральному углу 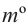 соответствует сектор площадь которого равна
соответствует сектор площадь которого равна 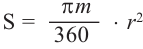 . Учитывая что радиальная мера центрального угла равна
. Учитывая что радиальная мера центрального угла равна 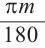 и обозначив её через
и обозначив её через 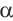 , запишем формулу нахождения площади сектора
, запишем формулу нахождения площади сектора 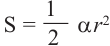 . Пример 1. Длина секундной стрелки часов равна 12 см. Определите длину дуги, которую описывает конец секундной стрелки за 15 секунд.
. Пример 1. Длина секундной стрелки часов равна 12 см. Определите длину дуги, которую описывает конец секундной стрелки за 15 секунд.
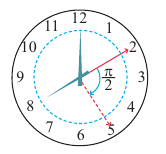
Решение. Секундная стрелка за 60 минут совершают один полный оборот. Это соответствует 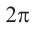 радианам. 15 секунд соответствуют
радианам. 15 секунд соответствуют 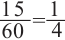 части полного оборота:
части полного оборота: 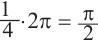 радиан. То есть, минутная стрелка за 15 секунд чертит дугу, соответствующую центральному углу
радиан. То есть, минутная стрелка за 15 секунд чертит дугу, соответствующую центральному углу 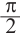 . Длина этой дуги:
. Длина этой дуги: 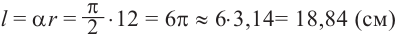
Пример 2. Найдите площадь и периметр закрашенного сектора на рисунке, если радиус круга равен 8 см. Закрашенной части круга соответствует центральный угол: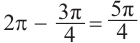
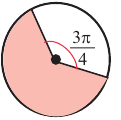
Площадь сектора равна:
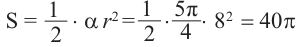 (см2).
(см2).
Периметр сектора равен сумме длин двух радиусов и длины дуги: 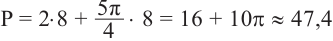 (см)
(см)
Линейная скорость и угловая скорость
Скорость при движении по окружности, например, скорость движения произвольной точки Р колеса, которое вращается вокруг точки О, может быть вычислена двумя способами.
В первом случае, её можно найти используя расстояние и время. Эта скорость называется линейной скоростью. Во втором случае - используя угол поворота (центральный угол). Эта скорость называется угловой скоростью.
Если тело движется но окружности, то линейная скорость равна отношению пройденного пути (длины дуги окружности) к промежутку времени.
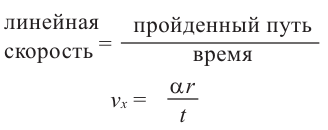
Если тело движется по окружности, то угловая скорость равна отношению угла поворота к промежутку времени.
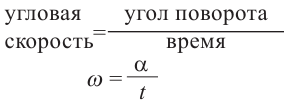
 Здесь
Здесь 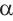 (в радианах) - угол вращения за промежуток времени
(в радианах) - угол вращения за промежуток времени 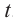 . Между линейной и угловой скоростью существует следующая связь:
. Между линейной и угловой скоростью существует следующая связь:
линейная скорость = 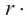 угловая скорость
угловая скорость
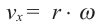
Пример 3. Карусель совершает за минуту 8 полных оборотов.

а)Чему равна угловая скорость карусели за минуту(в радианах)?
б)На сколько метров за минуту передвигается лошадь, которая находится на расстоянии 3 м от центра окружности?
в)На сколько метров за минуту передвигается лошадь, которая находится на расстоянии 2 м от центра окружности?
Решение:
а) Один целый оборот при вращении соответствует центральному углу 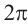 . За 8 оборотов этот угол равен
. За 8 оборотов этот угол равен 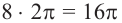 . Угловая скорость за минуту равна
. Угловая скорость за минуту равна 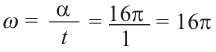 радиан/мин.
радиан/мин.
б)Если лошадь находится на расстоянии 3 м от центра, то она движется по окружности радиуса 3 м.
Линейная скорость: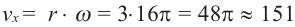 м/мин
м/мин
в)Если лошадь находится на расстоянии 2 м от центра, то она движется по окружности радиуса 2 м.
Линейная скорость: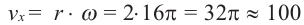 м/мин
м/мин
Тригонометрические функции
Тригонометрические отношении для угла зависят только от значения угла.
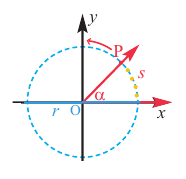
Пусть конечная сторона угла а при повороте пересекается с окружностью радиусом г, центр которой находится в начале координат, в точке Р(х; у).
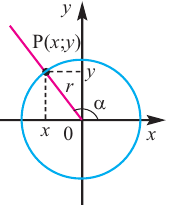
 Отношение ординаты точки Р к длине радиуса называется синусом угла
Отношение ординаты точки Р к длине радиуса называется синусом угла 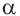 :
: 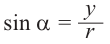
 Отношение абсциссы точки Р к длине радиуса называется косинусом угла
Отношение абсциссы точки Р к длине радиуса называется косинусом угла 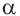 :
: 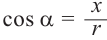
 Отношение ординаты точки Р к абсциссе называется тангенсом угла
Отношение ординаты точки Р к абсциссе называется тангенсом угла 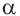 :
:
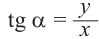 (здесь
(здесь 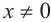 , то есть точка Р не расположена на оси ординат)
, то есть точка Р не расположена на оси ординат)
 Отношение абсциссы точки Р к ординате называется котангенсом угла
Отношение абсциссы точки Р к ординате называется котангенсом угла 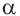 :
: 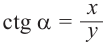 (здесь
(здесь 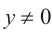 , то есть точка Р не расположена на оси абсцисс)
, то есть точка Р не расположена на оси абсцисс)
 Косинусом угла
Косинусом угла 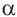 называется обратное значение для синуса:
называется обратное значение для синуса:
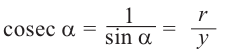 (здесь
(здесь 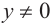 )
)
 Секансом угла
Секансом угла 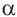 называется обратное значение для косинуса:
называется обратное значение для косинуса:
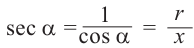 (здесь
(здесь 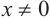 )
)
Пример 1. Точка А (- 3; 4) расположена на конечной стороне угла поворота 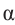 .
.
а) Изобразите решение примера.
б) Определите значения тригонометрических отношений для угла поворота 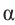 .
.
Решение:
а)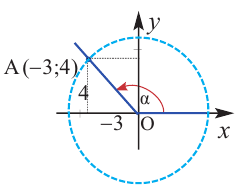
б)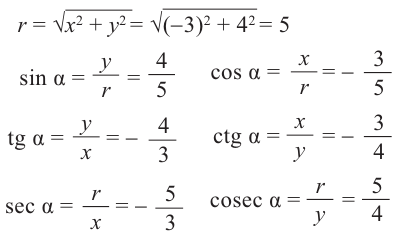
Координаты точки на окружности
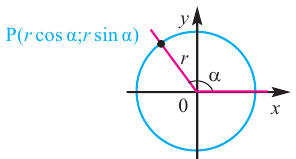
Если заданная точка Р окружности находится на конечной стороне угла поворота 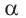 , то она имеет координаты
, то она имеет координаты 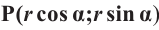 .
.
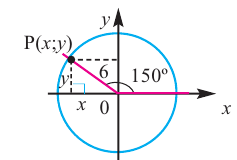
Пример 2. По данным рисунка найдите координаты точки Р.
Точка Р находится во II четверти и косинус отрицательный.
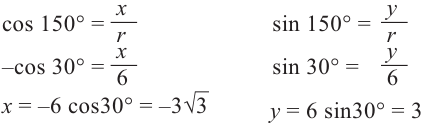 Для некоторых углов, конечная сторона расположена на одной из координатной оси. В этом случае, градусная мера угла поворота равна:
Для некоторых углов, конечная сторона расположена на одной из координатной оси. В этом случае, градусная мера угла поворота равна: 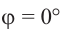 или
или 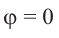 радиан,
радиан, 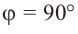 или
или 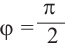 радиан,
радиан, 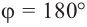 или
или 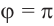 радиан,
радиан, 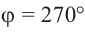 или
или 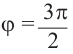 радиан.
радиан.
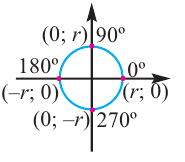
В этом случае координаты х или у равны или нулю, или абсолютному значению длины радиуса.
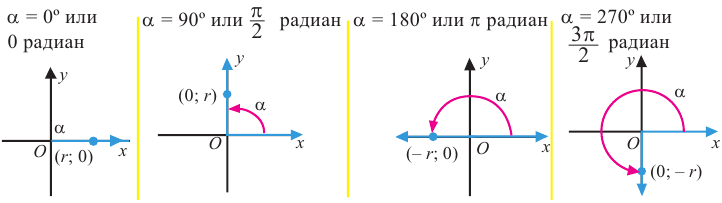
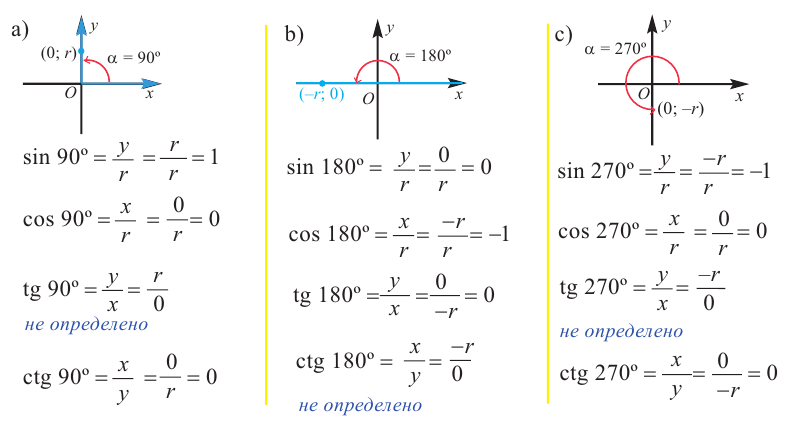
Пример 3. Найдём значения тригонометрических отношений для:
а) а = 90° ; б) а = 180°; в) а = 270° .
При всех допустимых значениях, каждому значению 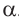 , соответствует единственное значение
, соответствует единственное значение 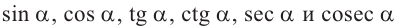 . Поэтому тригонометрические отношения являются функциями угла
. Поэтому тригонометрические отношения являются функциями угла 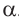 и называются тригонометрическими функциями.
и называются тригонометрическими функциями.
Так как 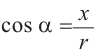 , то знак косинуса совпадает со знаком х.
, то знак косинуса совпадает со знаком х.
Так как 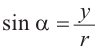 , то знак синуса совпадает со знаком у.
, то знак синуса совпадает со знаком у.
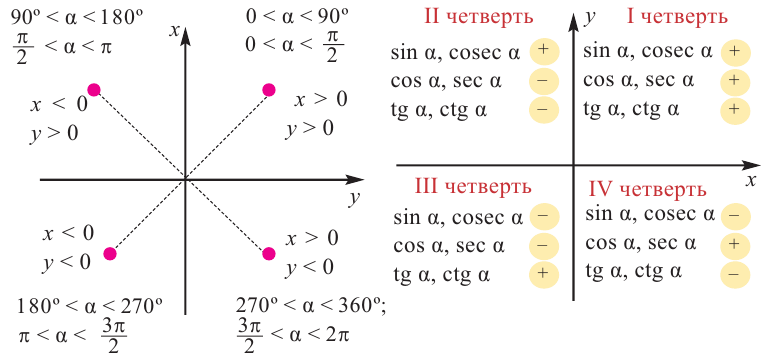
Тригонометрические функции произвольного угла. Нахождение значений тригонометрических функций произвольного угла при помощи острого угла
Чтобы вычислить тригонометрические отношения для углов больше 90°, удобно использовать тригонометрические отношения острого угла.
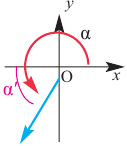
Для любого угла поворота 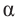 существует
существует 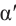 образованный конечной стороной и прямой, содержащий ось абсцисс.
образованный конечной стороной и прямой, содержащий ось абсцисс.
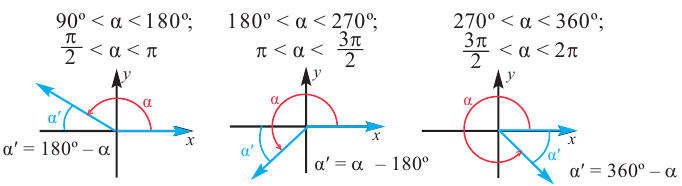
Используя соответствующие острые углы можно определить тригонометрические отношения для любого произвольного угла. Эти значения можно вычислить точно для углов 30°, 45°, 60°, а для остальных острых углов - при помощи калькулятора.
Пример 1. Для следующих углов, определите острые углы:
а)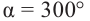 б)
б)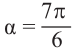
Решение:
а) конечная сторона угла 300° расположена в IV четверти. Соответствующий острый угол равен: 360°- 300° = 60°
б) конечная сторона угла расположена в III четверти. Соответствующий
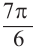 острый угол равен:
острый угол равен: 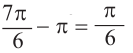
Пример 2. Найдём значение основных тригонометрических функций для угла 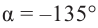 . Шаги решения:
. Шаги решения:
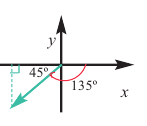
1.Найдём наименьший положительный угол, конечная сторона которого совпадает с заданным углом и дополняет его до 360°: -135° + 360° = 225°
2.Для угла 225° найдём соответствующий острый угол 225° - 180° = 45°.
3.Определим какой четверти принадлежит угол -135° - угол III четверти.
4.Найдём значение тригонометрических функций для угла 45° и учтём знак этих функций в III четверти. Получим:
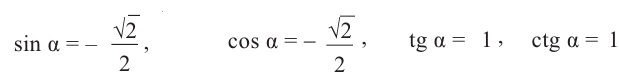 Тригонометрические функции для произвольного угла можно определить следующим образом:
Тригонометрические функции для произвольного угла можно определить следующим образом:
•определяем соответствующий острый угол;
•находим значение тригонометрических функций для этого угла;
•определяем знак значения тригонометрических функций в зависимости от четверти.
Так как конечные стороны углов 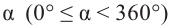 и
и 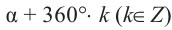 совпадают, то значения тригонометрических функций этих углов одинаковы. Если угол изменяется на целое число оборотов, то значение тригонометрических функций не меняется.
совпадают, то значения тригонометрических функций этих углов одинаковы. Если угол изменяется на целое число оборотов, то значение тригонометрических функций не меняется.

Заметим, что если угол меняется на пол оборота, то значения тангенса и котангенса не изменяются.
На самом деле, если углу поворота 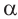 соответствует точка
соответствует точка 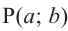 , а углу поворота
, а углу поворота 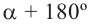 (или
(или  ) соответствует точка
) соответствует точка 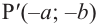 , то :
, то :
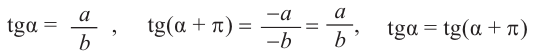
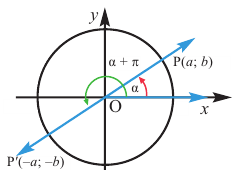 В общем случае
В общем случае 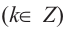 выполняются равенство:
выполняются равенство:
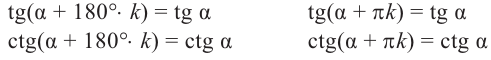
Пример 3. Найдём допустимые значения 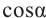 , если
, если 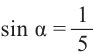 . Так как в I и во II четвертях синус положителен.
. Так как в I и во II четвертях синус положителен.
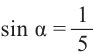 , значит если
, значит если 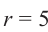 , то
, то 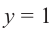
Абсцисса этой точки 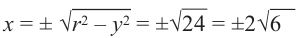
Тогда 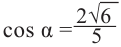 или
или 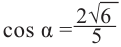
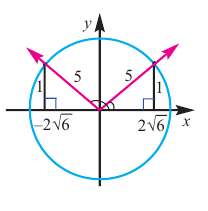
Единичная окружность и тригонометрические функции
Значения тригонометрических функций зависят только от значения угла 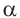 и не зависят от радиуса окружности. Поэтому, не нарушая общности, можно принять
и не зависят от радиуса окружности. Поэтому, не нарушая общности, можно принять 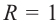 . Окружность, центр которой находится в начале координат, с радиусом равным единице, называется единичной окружностью. Координаты точки, принадлежащей окружности удовлетворяют уравнению
. Окружность, центр которой находится в начале координат, с радиусом равным единице, называется единичной окружностью. Координаты точки, принадлежащей окружности удовлетворяют уравнению 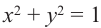 .
.
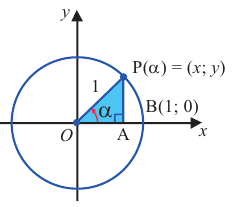
Если точка 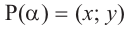 является точкой пересечения единичной окружности и конечной стороны угла поворота
является точкой пересечения единичной окружности и конечной стороны угла поворота 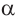 , то между ней и тригонометрическими функциями существует следующая связь:
, то между ней и тригонометрическими функциями существует следующая связь: 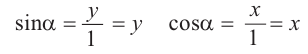 Таким образом, координаты точки принадлежащей единичной окружности, можно записать как:
Таким образом, координаты точки принадлежащей единичной окружности, можно записать как: 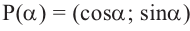 .
.
Также по заданным координатам можно найти следующие тригонометрические функции: 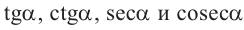 .
. 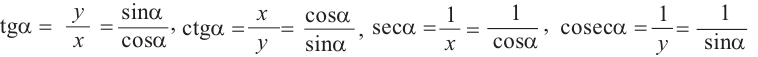 Зная, что
Зная, что 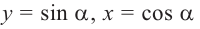 при определённом повороте на единичной окружности, можно найти соответствующие координаты точки.
при определённом повороте на единичной окружности, можно найти соответствующие координаты точки.
Для этого надо выполнить следующие шаги:
1) На единичной окружности отметим точки, соотвегствующие углу поворота 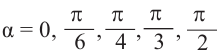 , найдём координаты этих точек по формуле:
, найдём координаты этих точек по формуле: 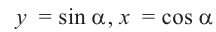 .
. 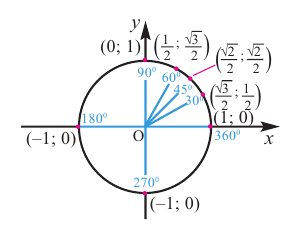
2)Для некоторой точки, принадлежащей единичной окружности, например 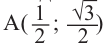 ,определите координаты симметричной точки. Как видно но рисунку, существует 3 точки, симметричные точке А, которые расположены во II, III и IV четвертях.
,определите координаты симметричной точки. Как видно но рисунку, существует 3 точки, симметричные точке А, которые расположены во II, III и IV четвертях.
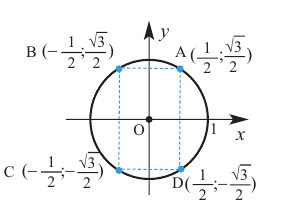
Точка В симметрична точке А относительно оси у, точка С - относительно начала координат, а точка D - относительно оси х. Абсолютные значения координат этих точек равны и отличаются только знаком.
3)Таким образом, можно определить координаты новых точек, зная координаты точки, принадлежащей I четверти. Т.е. получаем единичную окружность, на которой отмечены углы поворота и координаты точек.
Единичная окружность и тригонометрические функции произвольного угла
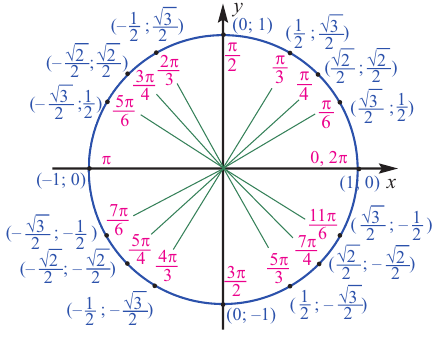
Так как координаты точек на единичной окружности удовлетворяют условиям 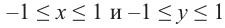 , то
, то 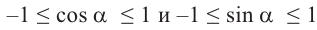 Наибольшее значение
Наибольшее значение 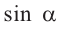 и
и 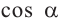 равно 1, а наименьшее значение равно -1.
равно 1, а наименьшее значение равно -1.
Пример 1. Для угла поворота 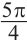 вычислите значения основных тригонометрических функций.
вычислите значения основных тригонометрических функций.
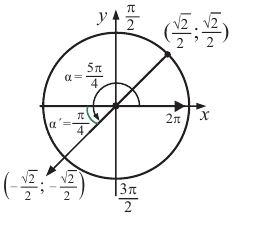
Решение: Конечная сторона угла поворота 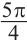 расположена в III четверти. Этому углу соответствует острый угол
расположена в III четверти. Этому углу соответствует острый угол 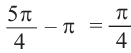 . Точка пересечения конечной стороны угла
. Точка пересечения конечной стороны угла 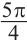 с единичной окружностью симметрична точке
с единичной окружностью симметрична точке 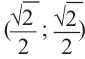 относительно начала координат и соответствует точке
относительно начала координат и соответствует точке 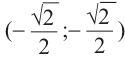 .
.
Тогда ,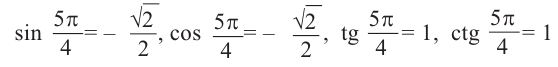
Пример 2. Точка А, с абсциссой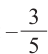 расположена в III четверти и пересекается с единичной окружностью на стороне угла
расположена в III четверти и пересекается с единичной окружностью на стороне угла 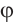 .
.
а)Найдём ординату точки А.
б)Изобразим рисунок, соответствующий условию и для угла 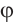 найдём значения шести тригонометрических функций.
найдём значения шести тригонометрических функций.
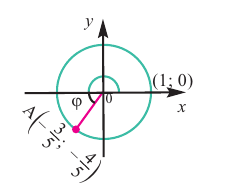
Решение:
а)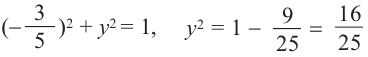 ,
, 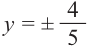 . Так как точка расположена в III четверти
. Так как точка расположена в III четверти 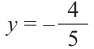 .
.
б)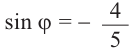 ,
,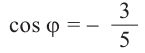 ,
,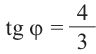 ,
,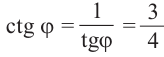 ,
,
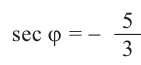 ,
,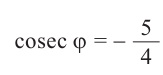 .
.
Пример 3. Найдём наибольшее и наименьшее значение выражения 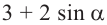 .
.
Решение:
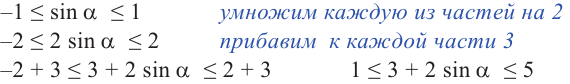
Таким образом, для выражения 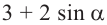 a НМЗ равно 1, а НБЗ равно 5.
a НМЗ равно 1, а НБЗ равно 5.
Формулы приведения
Если объект находится в I четверти, то симметричный ему относительно оси у объект находится во II четверти. Симметричный последнему относительно оси х, объект находится в III четверти, и он совпадает с объектом, симметричным начальному объекту из I относительно начала координат. Обратите внимание, что отображение относительно оси у и отображение, относительно оси х, совпадают с поворотом на 180°.
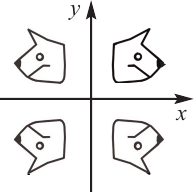
При отображении относительно оси х, точка расположенная на конечной стороне угла изменяет координаты, как показано на рисунке.
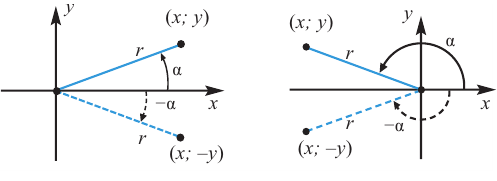
То есть, при этом знак меняет только координата у. Таким образом, так как косинус зависит от х он не меняется, зато меняется знак синуса. Отсюда, для углов 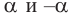 можно записать следующие зависимости между тригонометрическими функциями.
можно записать следующие зависимости между тригонометрическими функциями.
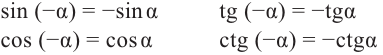
То есть, синус, тангенс и котангенс нечётные функции, косинус-чётная.
Пример 1:
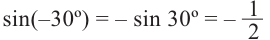
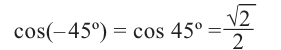
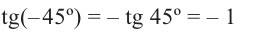
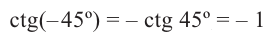 Конечные стороны углов поворота
Конечные стороны углов поворота  и 360° -
и 360° - 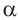 симметричны относительно оси х. То есть
симметричны относительно оси х. То есть 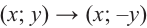 .
.
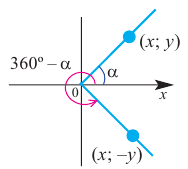
Отсюда получаем:

Запишем для углов  и 90° -
и 90° -  прямоугольного треугольника с острым углом
прямоугольного треугольника с острым углом  тригонометрические отношения:
тригонометрические отношения:
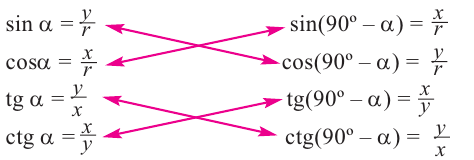
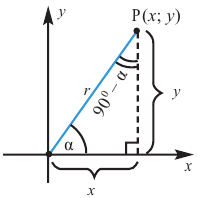
При попарном сравнении равенств можно увидеть следующую связь-между значениями тригонометрических функций углов  и 90° -
и 90° -  .
.
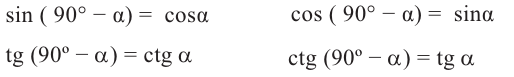
Повернём конечную сторону угла поворота  ещё на 90°. При этом точка Р(х; у), расположенная на стороне преобразуется в точку
ещё на 90°. При этом точка Р(х; у), расположенная на стороне преобразуется в точку 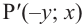 . По определению тригонометрических функций:
. По определению тригонометрических функций:
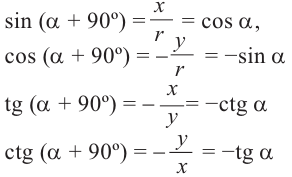
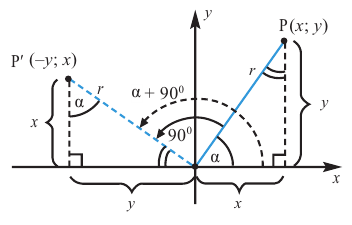
Запишем эти формулы в следующем виде: 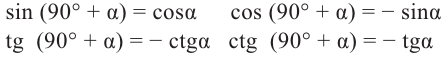
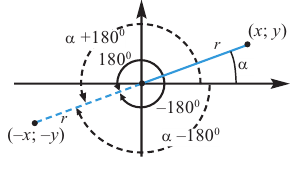
Как видно но рисунку отображения относительно оси у и оси х эквивалентны повороту на 180°. Изменение координат, можно записать следующим образом: 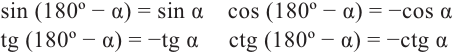
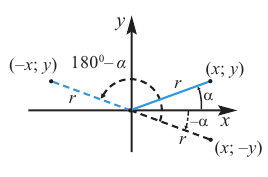
Как видно по рисунку, при повороте угла а на 180° конечная сторона расположена в противоположных четвертях, но на одной прямой.
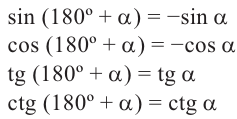
Пример 2. 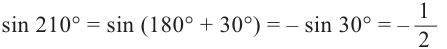
Для получения аналогичных формул тригонометрических функций угла поворота 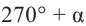 достаточно записать
достаточно записать 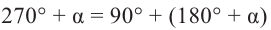 и применить последовательность соответствующих формул.
и применить последовательность соответствующих формул.
Например:
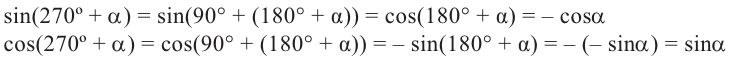
Теперь запишем соответствующие формулы для угла поворота 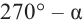 . Например:
. Например:
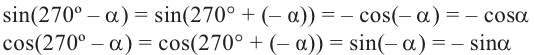
При помощи полученных формул можно найти значения тригонометрических функций произвольного угла, зная значения для соответствующего острого угла. Эти формулы называются формулами приведения. Для формул приведений можно легко увидеть следующую закономерность 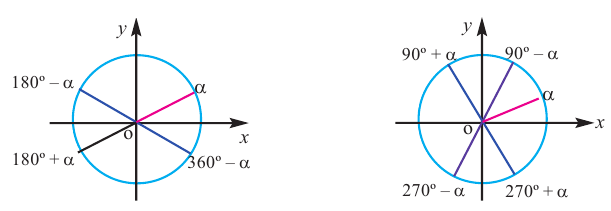
1)Если аргумент имеет вид 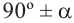 или
или 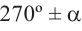 , то функция преобразуется в "сопряжённую" функцию (то есть синус в косинус или наоборот, а тангенс в котангенс или наоборот) угла
, то функция преобразуется в "сопряжённую" функцию (то есть синус в косинус или наоборот, а тангенс в котангенс или наоборот) угла 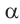 .
.
2)Если аргумент имеет вид 180° ± 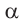 или 360° ±
или 360° ± 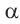 , то функция преобразуется в одноимённую функцию угла
, то функция преобразуется в одноимённую функцию угла 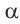 .
.
В каждом из обоих случаев, знак полученной в результате преобразования функции имеет одинаковое значение со знаком острого угла 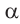 в соответствующей четверти.
в соответствующей четверти.
Тригонометрические тождества
Для острого угла 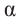 прямоугольного треугольника покажите, что
прямоугольного треугольника покажите, что 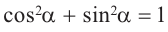 , выполнив следующие шаги:
, выполнив следующие шаги:
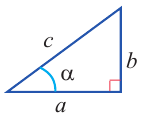
1)Запишите теорему Пифагора: 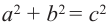
2)Каждую из сторон равенства разделите на с2:
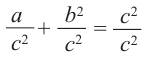
3)Примените свойство степени:
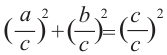
4) Примите во внимание, что: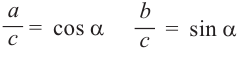
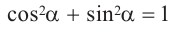
Связь между тригонометрическими функциями одного и того же угла
Тождество 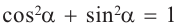 можно доказать и при помощи координат точки, принадлежащей единичной окружности.
можно доказать и при помощи координат точки, принадлежащей единичной окружности.
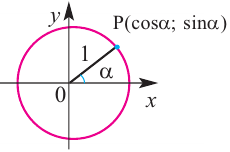
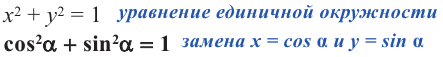
По координатам точки на единичной окружности и по определениям тригонометрических функций имеем:
Для всех значений 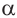 , при которых
, при которых 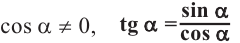
Для всех значений 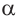 , при которых
, при которых 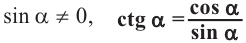
Из данных равенств имеем,что если для угла 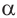 одновременно выполняются условия
одновременно выполняются условия 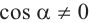 и
и 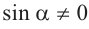 , то справедливо тождество
, то справедливо тождество 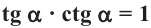
Разделив обе чаете равенства 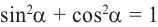 поочередно на
поочередно на 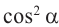 и на
и на 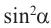 будем иметь:
будем иметь: 
Полученные выше равенства являются тождествами. Их называют основными тригонометрическими тождествами. На основании основных тригонометрических можно написать: 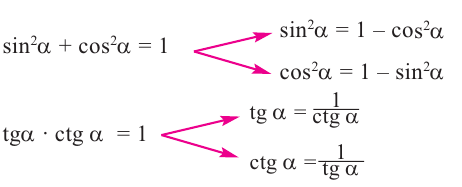
При помощи основных тригонометрических тождеств можно упрощать тригонометрические выражения и вычислять модуль значения всех остальных функций, зная значение одной из них.
Пример 1. Используя основные тригонометрические тождества, докажите,что: 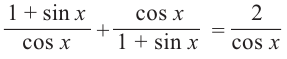
Доказательство:
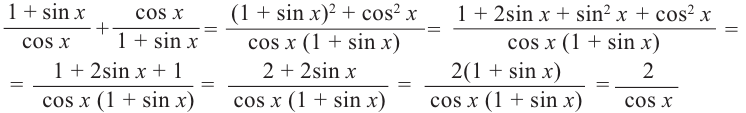
Пример 2. Зная, что 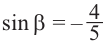 и угол
и угол 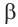 принадлежит III четверти, найдите
принадлежит III четверти, найдите
остальные тригонометрические функции.
Из формул 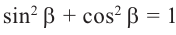 получаем:
получаем: 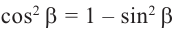
Так как угол 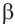 принадлежит III четверти, то
принадлежит III четверти, то
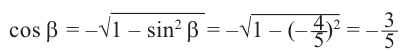
Тогда:
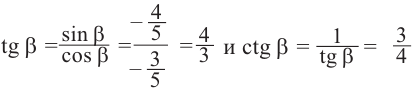
Формулы сложения
Практическая работа .
1)Покажем по шагам, равенство выражения 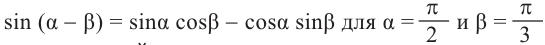
a)Для значений 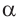 и
и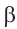 , вычислим значения выражения в левой части.
, вычислим значения выражения в левой части.
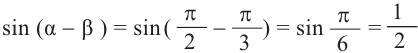 б)Для значений
б)Для значений 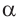 и
и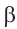 , вычислим значения выражения в правой части.
, вычислим значения выражения в правой части.
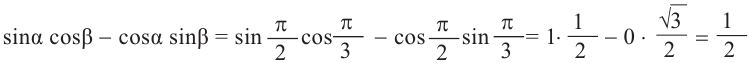
2)Как можно вычислить значение тригонометрических функций для угла 15°, используя разность значений углов 45° и 30°(15° = 45° - 30°)?
Тригонометрические функции суммы и разности двух углов.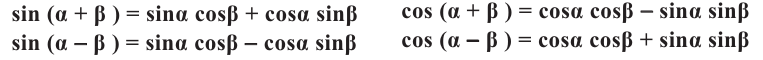
 Сначала докажем тождество
Сначала докажем тождество 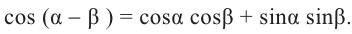
На рисунке
а)для угла 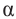 координаты точки Р1, взятой на единичной окружности равны
координаты точки Р1, взятой на единичной окружности равны 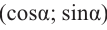 , а для угла
, а для угла 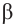 координаты точки Р2 равны
координаты точки Р2 равны 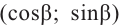 . Разместим углы
. Разместим углы 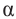 -
- 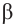 , как показано на рисунке б).
, как показано на рисунке б).
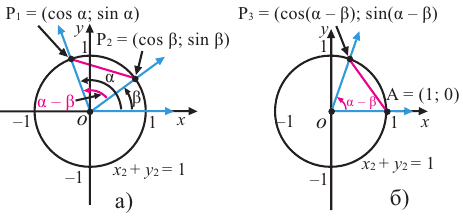
Тогда, для угла 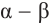 координаты точки Рз будут
координаты точки Рз будут 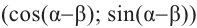 . Из того, что
. Из того, что 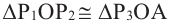 (по признаку СУС ) следует, что
(по признаку СУС ) следует, что 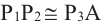 .
.

 Доказательство тождества
Доказательство тождества 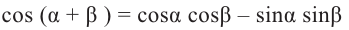
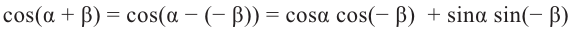
учитывая, что 
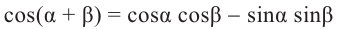 справедливость тождества доказана.
справедливость тождества доказана.
 Доказательство тождества
Доказательство тождества 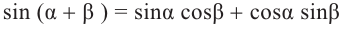
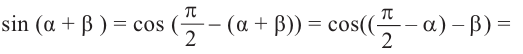
no формулам приведения группируя
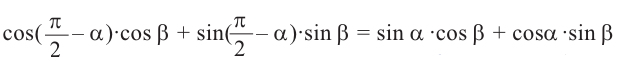
no формуле косинуса разности с учётом формул приведения.
 Доказательство тождества
Доказательство тождества 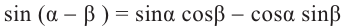 :
:
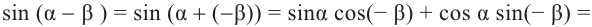
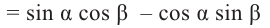
Пример 1. Найдём значение выражения 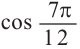 если
если
Решение.
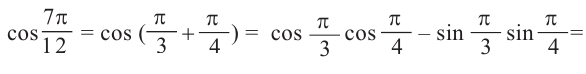
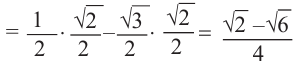
Пример 2.
Найдём значение выражения 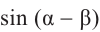 если
если
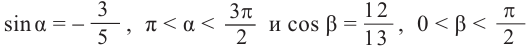 .
.
Решение.
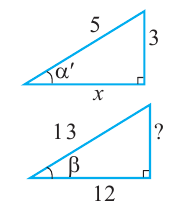
Известно что 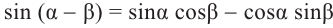 . Если углу
. Если углу 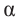 соответствует острый угол
соответствует острый угол 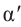 , то
, то 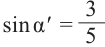 . Так как противолежащий катет равен 3, а гипотенуза 5, тогда прилежащий катет равен
. Так как противолежащий катет равен 3, а гипотенуза 5, тогда прилежащий катет равен 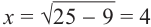 и учитывая, что
и учитывая, что 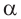 угол III четверти, получим:
угол III четверти, получим: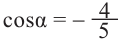 .
.
Аналогично, если зная, что 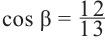 , получаем,
, получаем,
что 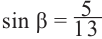 .
. 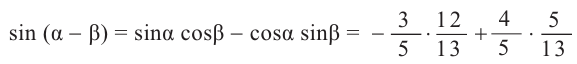
Можно записать формулы сложения для тангенса и котангенса: 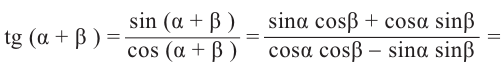
no определению no формулам сложения
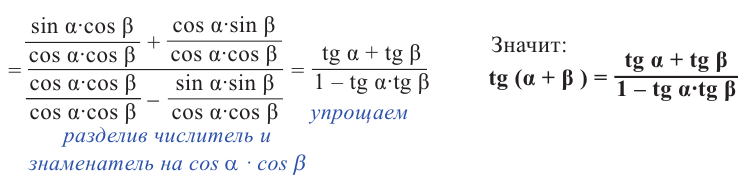
Аналогичным образом можно показать, что : 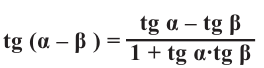
Следствия из формул сложения
Практическая работа.
Преобразуйте сумму 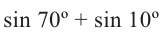 в произведение, выполнив следующие шаги:
в произведение, выполнив следующие шаги:
1) 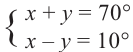
решив систему уравнений найдите такие углы, чтобы их сумма была равна 70°, а разность 
2)Запишите следующее 70° = 40° + 30°, 10° = 40° - 30° и упростите
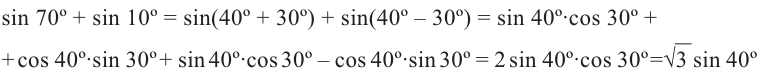
Преобразование суммы(разности) в произведение
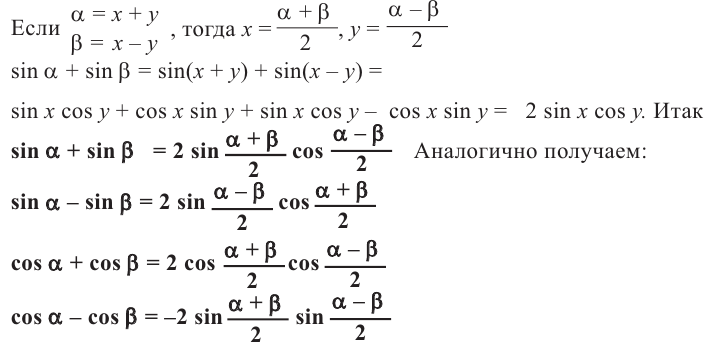
Формулы преобразования произведения
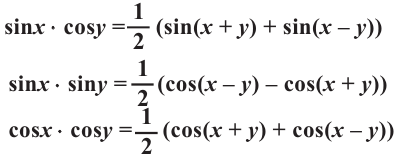
Справедливость данных тождеств можно показать при помощи формул сложения:
почленно складываем почленно складываем
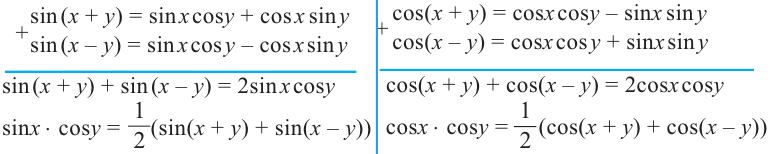
Следующее тождество можно доказать аналогичным образом.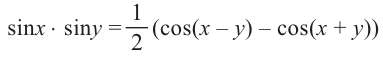
Тригонометрические функции двойного аргумента
Формулы сложения позволяют выразить 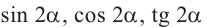 через тригонометрические функции угла
через тригонометрические функции угла 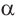 .
. 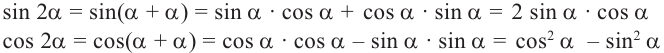
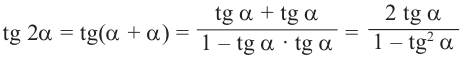
Таким образом, получаем тождества, которые называются формулами двойного аргумента:
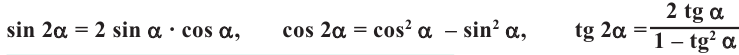
Формулы половинного аргумента
Имеем, что 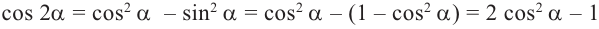
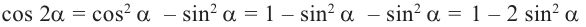
Отсюда: 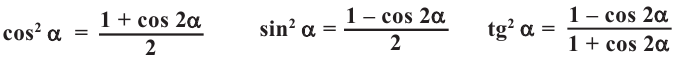 Заменяем в данной формуле
Заменяем в данной формуле 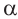 на
на 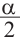 получаем:
получаем: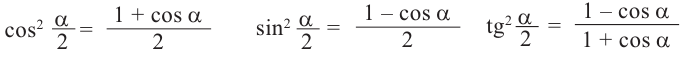
Для половинных аргументов справедливы тождества. 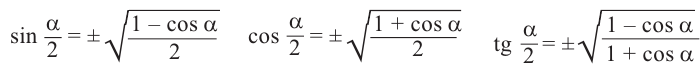 Знак в правой части в данном равенстве зависит от того, в какой четверги находится угол
Знак в правой части в данном равенстве зависит от того, в какой четверги находится угол 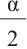 .
.
Пример 1. Упростим выражение  .
.
Решение. 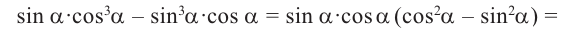
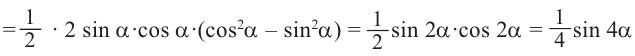
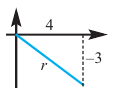
Пример 2. He используя калькулятор, вычислим значения 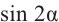 и
и 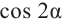 , зная, что угол
, зная, что угол  принадлежит IV четверти и
принадлежит IV четверти и 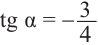
Решение.
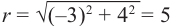

Пример 3. Найдём значений 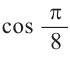 .
.
Решение:
Используем формулу половинного аргумента 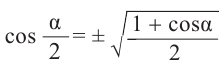
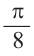 угол I четверти и в этой четверти косинус положителен.
угол I четверти и в этой четверти косинус положителен.
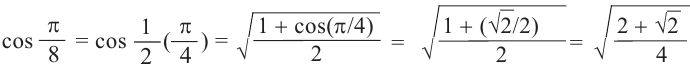
Упрощение тригонометрических выражений
Пример 1. Раскроем скобки и упростим выражение.
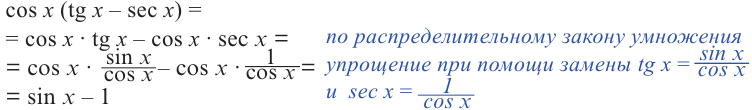
Пример 2. Разложим на множители и упростим выражение.

Пример 3. Упростим рациональное выражение, содержащее тригонометрические функции.

Пример 4. Освободим знаменатель от радикала 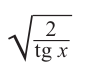
Здесь 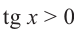 .
.
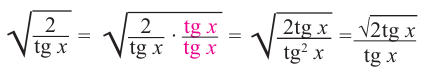
| Рекомендую подробно изучить предметы: |
| Ещё лекции с примерами решения и объяснением: |