Треугольники и окружность - задачи с примерами решения

Пример:

Длина катета ВС прямоугольного треугольника АСВ равна 15 см, а его катет АС является диаметром окружности, которая пересекает гипотенузу в точке F, CF =12 см. Вычислите радиус окружности.
 

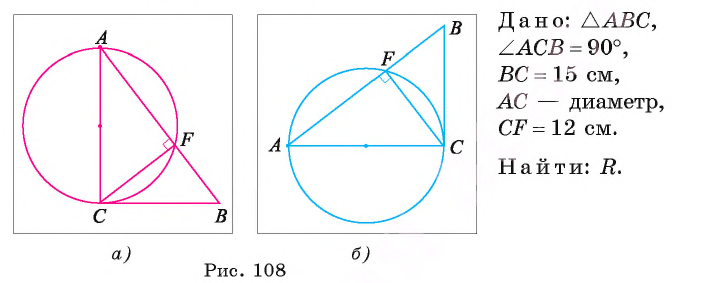
Решение:

Из условия следует, что радиус R равен половине катета АС. Заметим, что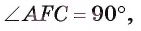

1) В треугольнике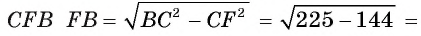

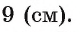
2) Воспользовавшись равенством 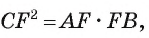найдем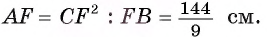 

3) Теперь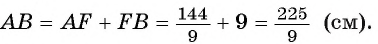

4) Квадрат длины катета прямоугольного треугольника равен произведению длины гипотенузы и длины проекции этого катета на гипотенузу, следовательно,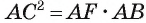

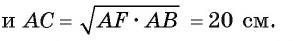
Таким образом,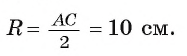

Ответ 10 см.

Пример:

Решение:

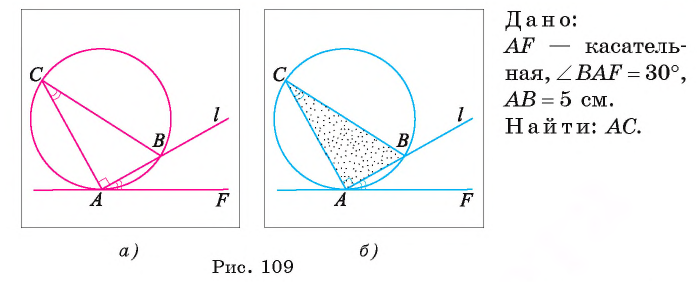
По теореме об угле между хордой и касательной 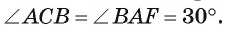Так как точки С и В диаметрально противоположные, то угол САВ опирается на диаметр, а следовательно, он прямой, т. е. треугольник САВ — прямоугольный (рис. 109, а, б). Расстояние от точки С до точки касания А равно длине катета СА треугольника САВ. Так как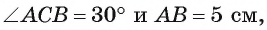

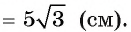
Ответ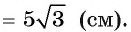 

Пример:

Вычислите радиус окружности, вписанной в равнобедренный треугольник ABC, если длина его основания АС равна 24 см, а высота BD, проведенная к основанию, равна 9 см.

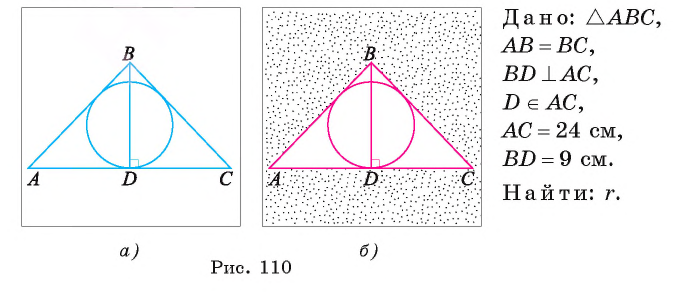
Решение:

Для вычисления радиуса г вписанной окружности воспользуемся формулой 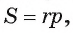где S — площадь треугольника, р — его полупериметр. Отсюда получим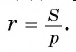

1) Площадь треугольника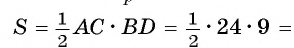

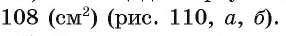
2) В прямоугольном треугольнике ADB длина катета

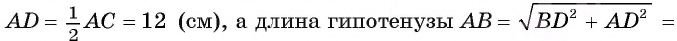
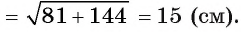
3) Теперь полупериметр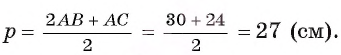

4) Таким образом, найдем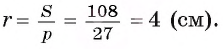

Ответ: 4 см.

Пример:

В равнобедренном треугольнике ABC с основанием АС на стороне ВС лежит точка D так, что 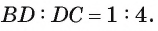В каком отношении точка О пересечения отрезка AD и высоты BE делит высоту BE, считая от вершины В?

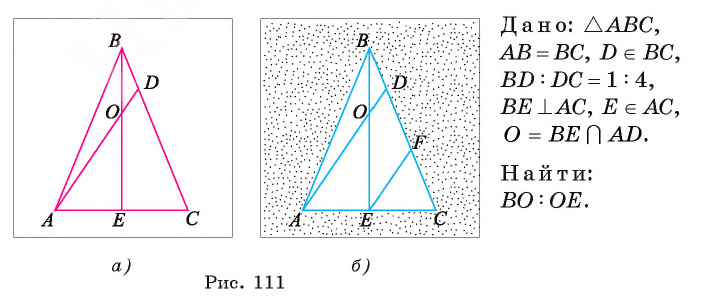
Решение:

1) Так как 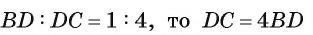(рис. 111, а, б). Проведем отрезок 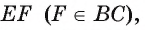, параллельный отрезку AD.

2) Так как высота, проведенная к основанию равнобедренного треугольника, является медианой, то точка Е — середина стороны АС.

3) По признаку средней линии отрезок EF — средняя линия треугольника ADC, значит,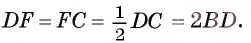

4) Так как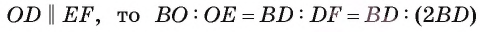     

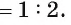
Ответ: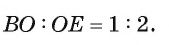

Пример:

Отрезки AF и СТ — высоты остроугольного треугольника ABC. Найдите радиус окружности, описанной около треугольника BTF, если A ABC = 60° и АС = b.
 

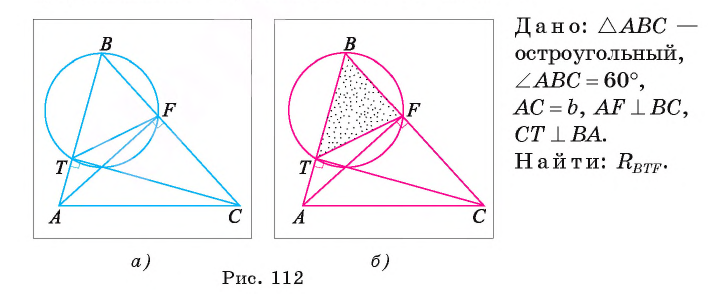
Решение:

Воспользуемся теоремой синусов и тем, что треугольник ABC подобен треугольнику BTF.

1) В треугольнике BTF по теореме синусов выполняется равенство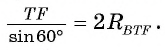Следовательно, 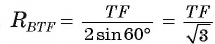(рис. 112, a, 6).

2) Рассмотрим треугольники ABC и FTC. Эти треугольники подобны. Действительно,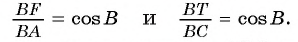

Следовательно,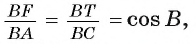т.е. треугольники подобны с коэффициентом подобия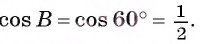

3) Из подобия треугольников ABC и FTC следует, что 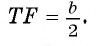Таким образом,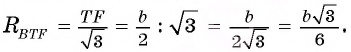 

Ответ: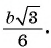

Пример:

Отрезок BD — биссектриса треугольника ABC. Известно, что 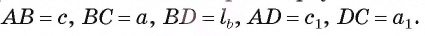Докажите, что 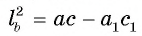(рис. 113, а).

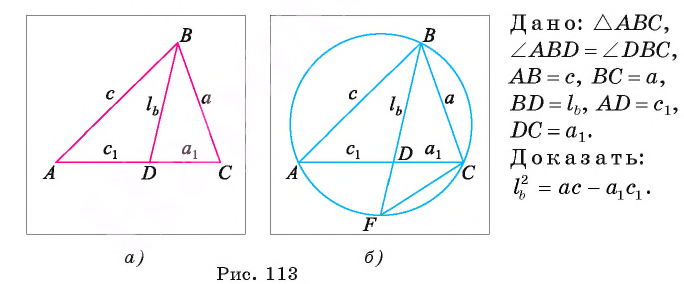
Доказательство.

Рассмотрим окружность, описанную около треугольника ABC. Пусть прямая BD пересекает окружность в точке F и DF = х (рис. 113, б).

1) По свойству отрезков пересекающихся хорд выполняется равенство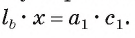

2) Треугольники ABD и FBC подобны, так как 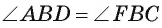по условию и  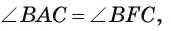поскольку являются вписанными в окружность и опираются на одну и ту же дугу.

3) Из подобия треугольников ABD и FBC следует, что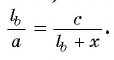 Отсюда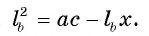

3) Таким образом,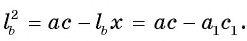

Что и требовалось доказать.