
Тождества с корнями, содержащие одну переменную с примерами решения
Содержание:
Корни 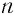
Теорема:
Пусть 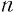 — нечетное число. Тогда при любом значении
— нечетное число. Тогда при любом значении 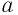 верны равенства:
верны равенства:

Доказательство:
Равенства (1) и (2), как и другие равенства в теоремах этого пункта, очевидно, верны при 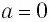 . Поэтому доказательства проводятся для
. Поэтому доказательства проводятся для 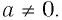
Рассмотрим равенство (1). Возведя его левую и правую части в 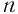 -ю степень, получим
-ю степень, получим 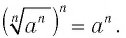
Согласно тождеству (1) из п. 1.2 это верное числовое равенство при любом значении 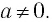 По следствию из п. 1.1 верно и равенство
По следствию из п. 1.1 верно и равенство
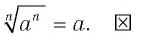
Равенство (2) доказывается аналогично: устанавливается, что 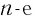 степени его левой и правой частей равны, и на основании следствия из п. 1.1 делается вывод об истинности равенства (2) при любом значении
степени его левой и правой частей равны, и на основании следствия из п. 1.1 делается вывод об истинности равенства (2) при любом значении 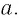
Аналогичными рассуждениями можно обосновать и остальные равенства в теоремах этого пункта.
Заметим, что каждое из этих равенств является тождеством, поскольку оно обращается в верное числовое равенство при любом значении переменной, при котором входящие в это равенство выражения имеют смысл.
Теорема:
Пусть 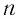 — четное число. Тогда при любом значении
— четное число. Тогда при любом значении 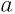 верно равенство:
верно равенство:

Теорема 3. Пусть 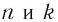 — натуральные числа. Тогда при любом неотрицательном значении
— натуральные числа. Тогда при любом неотрицательном значении 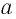 верны равенства:
верны равенства:

Заметим, что, когда оба числа 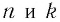 нечетные, равенства (4) и (5) верны для любых значений
нечетные, равенства (4) и (5) верны для любых значений 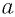 , а не только для неотрицательных.
, а не только для неотрицательных.
Равенство (5) означает, что при извлечении корня, из корня подкоренное выражение остается прежним, а показатели корней перемножаются.
Теорема:
Пусть 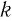 — целое число. Тогда при любом положительном значении
— целое число. Тогда при любом положительном значении 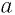 верно равенство
верно равенство

Примеры с решением
Пример №1
Найти значение 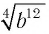 при:
при:

Решение:
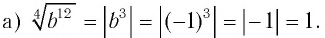
б) 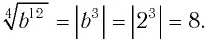
Ответ: 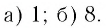
Пример №2
Сравнить числа 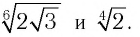
Решение:
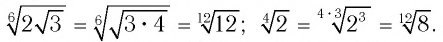
Поскольку верно неравенство 12 > 8, то будет верным и неравенство 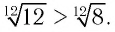 Следовательно,
Следовательно, 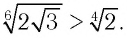
Ответ: 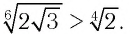
Пример №3
Решить уравнение:

Решение:
а) По определению корня 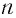 -й степени имеем, что данное уравнение равносильно уравнению
-й степени имеем, что данное уравнение равносильно уравнению 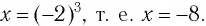
б) 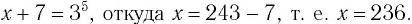
Ответ: 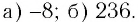
Пример №4
Решить уравнение 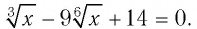
Решение:
Обозначим 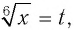 тогда
тогда 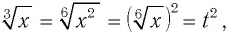 и получим уравнение
и получим уравнение
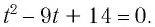
Корни этого уравнения 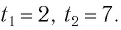
Таким образом, имеем: 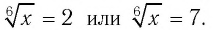
Решив эти уравнения, найдем:
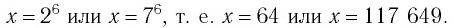
Ответ: 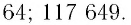
| Рекомендую подробно изучить предметы: |
| Ещё лекции с примерами решения и объяснением: |