Точка, прямая и плоскость в пространстве - определение и вычисление с примерами решения

Содержание:

Точка, прямая и плоскость в пространстве

В разделе планиметрии в геометрии изучаются фигуры, все точки которых лежат в одной плоскости. Эти фигуры называются плоскими фигурами. Однако в реальной жизни нас окружают трехмерные объекты. Их измерениями являются длина, ширина и высота(глубина). Эти фигуры называются пространственными фигурами, а раздел геометрии, который занимается изучением этих фигур, называется стереометрией. Принято считать, что точка, прямая и плоскость также являются пространственными фигурами. Плоскость бесконечна, и обычно, её условно изображают в виде параллелограмма и обозначают одной маленькой буквой или тремя буквами( указывающие три точки, не расположенные на одной прямой). Например, плоскость а или плоскость ABC.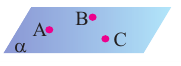

Аксиома 1. Какова бы ни была плоскость, существуют точки, принадлежащие этой плоскости, и точки, не принадлежащие ей.

Аксиома 2. Если у двух различных плоскостей есть общая точка, то они пересекаются по прямой, проходящей через эту точку.

Прямая задаётся двумя точками, то есть через две точки можно провести одну и только одну прямую (а сколько прямых можно провести через одну точку?). Сколькими точками задаётся плоскость? Двумя точками плоскость задать нельзя. Как видно по рисунку, через точки А и В можно провести бесконечно много плоскостей. Однако, среди этих плоскостей есть такая плоскость, что точка С расположена на ней. Значит, плоскость можно задать тремя точками, не лежащими на одной прямой.

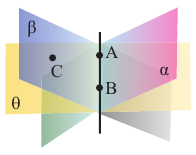
Аксиома 3. Через три точки, не лежащие на одной прямой можно провести плоскость и притом только одну.

Точки, расположенные на одной прямой, называются коллинеарными точками. Покажем, что если две точки прямой принадлежат плоскости, то все точки прямой принадлежат этой плоскости.

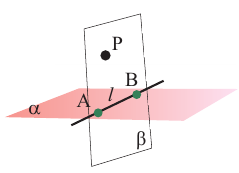
Пусть, точки А и В прямой 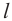принадлежат плоскости а. Возьмём точку Р, которая не принадлежит прямой 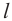и плоскости а. Через точки Р, А и В проведём плоскость 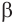. Так как плоскости а и 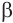пересекаются по линии, проходящей через точки А и В, то она совпадает с прямой 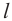. Все точки линии пересечения принадлежат плоскости а, т.е. все точки прямой 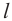также принадлежат плоскости а. Из аксиом стереометрии вытекают следующие следствия.

1. Через прямую и точку вне её можно провести плоскость и притом только одну.
2. Через две пересекающиеся прямые можно провести плоскость и притом только одну.
3. Через две параллельные прямые можно провести плоскость и притом только одну.

Таким образом плоскость можно задать:

1. прямой и точкой не принадлежащей этой прямой;
2. двумя пересекающимися прямыми;
3. двумя параллельными прямыми.

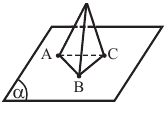
Пример. Даны три точки А, В и С, не лежащие на одной прямой и точка Р, не лежащая с ними в одной плоскости. Запишите названия всех плоскостей, проходящих через каждые три из них.

Решение:

Через точки А, В и С проведём плоскость а и отметим точку Р вне этой плоскости. Через эти точки можно провести 4 плоскости - АВР, ВРС, ABC и APC.

Точки, принадлежащие одной плоскости, называются компланарными. Точки А, В, С и Р из примера некомпланарные.

Взаимное расположение прямых в пространстве

Две прямые в пространстве могут быть параллельными (в частном случае совпадать) или пересекаться.

Известно, что если прямые 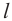и 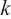пересекаются или параллельны, то они лежат в одной плоскости. В планиметрии эти два случая соответствуют пересечению или параллельности прямых.

Если две пересекающиеся прямые пересекаются с третьей в разных точках, то эти прямые расположены в одной плоскости. Если две пересекающиеся прямые, пересекаются с третьей в одной точке, то они могут быть расположены как в одной плоскости, так и в разных.

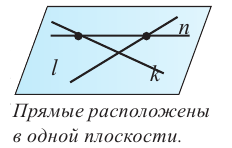
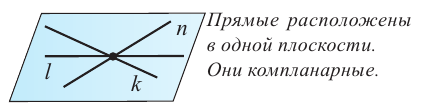
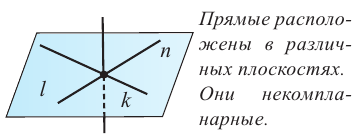
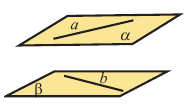
Две не параллельные прямые в пространстве не всегда пересекаются. Прямые, которые не параллельны и не пересекаются, называются скрещивающимися прямыми. Скрещивающиеся прямые а и b обозначаются так: . Через скрещивающиеся прямые нельзя провести плоскость. Углу между скрещивающимися прямыми соответствует угол, между параллельными им и пересекающимися прямыми.

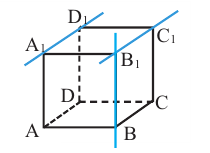
Пример. На модели куба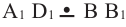 . Так как 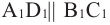, то угол между скрещивающимися прямыми А₁ D₁ и В В₁ равен углу между прямыми В₁С₁ и В В₁ , т.е. 90°.

Теорема 1. (Признак параллельности прямой и плоскости) Если прямая, не лежащая в данной плоскости, параллельна какой-нибудь прямой на этой плоскости, то эта прямая параллельна данной плоскости.

Доказательство. Пусть прямая а, не принадлежащая плоскости а параллельна прямой b, принадлежащей этой плоскости. Через прямые а и b проведём плоскость 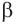. Тогда плоскости а и 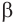пересекаются по прямой b. Если прямая а пересекает плоскость а, то точка пересечения должна быть расположена на прямой b , что невозможно при 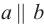. Значит .

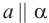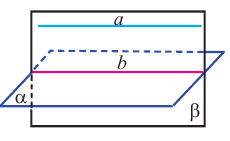
Следствие. Если плоскость проходит через прямую, параллельную другой плоскости и пересекает эту плоскость, то линия пересечения параллельна этой прямой.

Следствие. Если прямая параллельна каждой из двух пересекающихся плоскостей, то она параллельна линии их пересечения.

Теорема 2. Если плоскости, проходящие через две параллельные прямые пересекаются, то линия пересечения параллельна этим прямым.

Доказательство: предположим, что а || b. Проведём плоскости 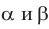соответственно через прямые а и b. Обозначим линию пересечения через с. По признаку параллельности прямой и плоскости . Отсюда а || с. Аналогично, если 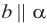, то b || с.

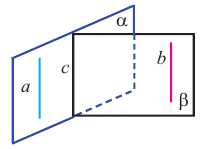
Теорема 3. Две прямые параллельные третьей, параллельны между собой.

Доказательство: утверждение верно для прямых, лежащих в одной плоскости. Пусть прямые а, b и с не лежат в одной плоскости и а || с, b || с. Проведём плоскость 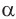через прямые а и с. Если b || с, то b || 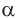. Возьмём на прямой а точку М и через неё и прямую b проведём плоскость 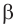. Линия пересечения плоскосте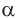й и 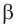, прямая МN, параллельна прямым b и с. Из точки М к прямой с можно провести только одну параллельную прямую. Поэтому прямые МN и а совпадают. Из того, что МN || b , получаем а || b.

Перпендикулярность прямой и плоскости

Определение. Если прямая (a), пересекающая плоскость 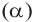, перпендикулярна каждой прямой, которая лежит в данной плоскости и проходит через точку пересечения, то прямая (а) перпендикулярна плоскости 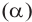и это записывается так: .

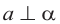Теорема 1. (Признак перпендикулярности прямой и плоскости). Если прямая, пересекающая плоскость, перпендикулярна двум прямым в этой плоскости, то она перпендикулярна плоскости.

Дано. Пересекающиеся прямые а и b принадлежат плоскости .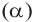

, .

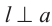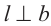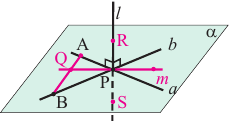
Доказать, что. .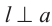

Пусть прямые а и b пересекаются в точке Р, принадлежащей плоскости 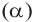и прямая перпендикулярна точке Р. Проведём в плоскости а через точку Р произвольную прямую m и прямую, проходящую через точки А, В и Q , соответствующих прямых а, b и m. Начиная от точки Р на прямой отметим конгруэнтные отрезки РR и РS. Выполним доказательство в следующей последовательности.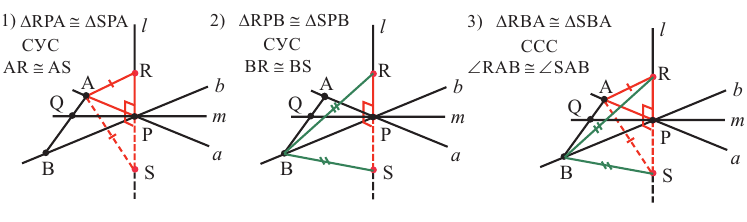

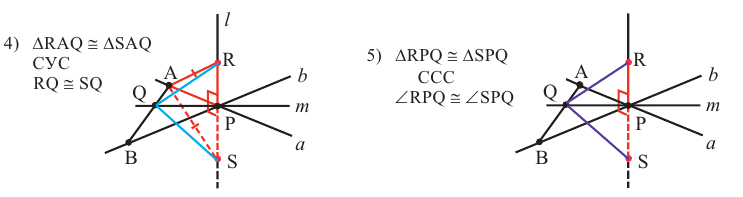
В равнобедренном треугольнике 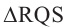, отрезок РQ является и медианой и высотой. Отсюда 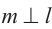. По определению имеем 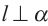. Теорема доказана.

По рисунку видно, что прямая перпендикулярная плоскости в точке пересечения, перпендикулярна любой прямой в данной плоскости.

Теорема 2. Через точку на прямой можно провести перпендикулярную ей плоскость и притом только одну.

Теорема 3. Через точку на плоскости можно провести перпендикулярную ей прямую и притом только одну.

Докажем теорему 3.

Дано: прямая 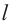перпендикулярная плоскости 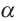в точке Р.

Доказать, что : через точку Р можно провести единственную прямую

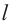, перпендикулярную плоскости .

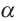Доказательство. Докажем теорему от обратного. Предположим, что существует ещё одна прямая z , перпендикулярная плоскости 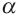в точке Р. Прямые 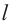и z лежат в плоскости 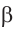, пересекающей плоскость 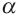вдоль прямой b. При пересечении прямых 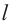и z образуется угол 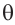. По определению перпендикулярной прямой и плоскости прямая 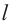(как и прямая z ) перпендикулярна любой прямой в плоскости 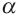, в том числе и прямой b.

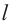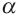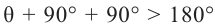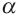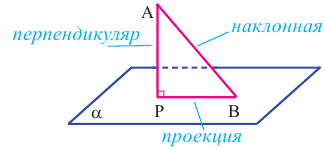
Тогда и прямая , и прямая z должны быть перпендикулярны плоскости . Однако, это невозможно, так как . Таким образом, через точку Р в плоскости можно провести одну и только одну перпендикулярную прямую. Если в пространстве, через точку А провести перпендикулярную прямую, которая пересекает плоскость 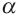в точке Р, то отрезок АР называется перпендикуляром из точки А к плоскости 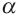. Отрезок, соединяющий точку А с любой точкой (отличной от точки Р) в плоскости 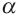называется наклонной.

Отрезок АР - перпендикуляр к плоскости.

Отрезок АВ - наклонная.

Точка Р - основание перпендикуляра.

Точка В - основание наклонной.

Отрезок ВР называется проекцией наклонной на плоскость. Если из точки к плоскости провести перпендикуляр и наклонную, то:

1)перпендикуляр меньше наклонной;

2)равные наклонные имеют равные проекции;

3)большая наклонная имеет большую проекцию.

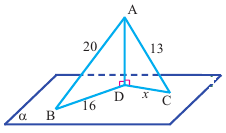
Пример. Из точки на плоскость проведены две наклонные длиной

20 см и 13 см. Найдите длину меньшей проекции, если длина большей проекции равна 16 см.

Решение: АР перпендикуляр, АВ и АС наклонные. Пусть ВО и СО являются проекциями наклонных. Из 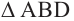по теореме Пифагора:

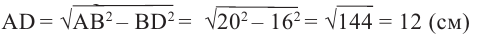
Из 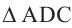по теореме Пифагора:

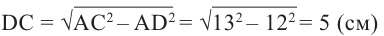
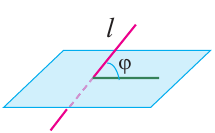
Углом между прямой и плоскостью

Углом между прямой и плоскостью называется угол между наклонной и её проекцией на плоскость.

Угол между прямой и плоскостью не больше углов, образованных этой прямой и любой другой прямой в плоскости.

В случае, если прямая перпендикулярна плоскости, то угол между ними равен

90°.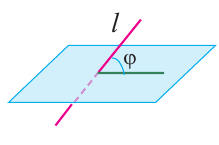

Теорема о трех перпендикулярах

Теорема. Если прямая на плоскости перпендикулярна проекции наклонной, то она перпендикулярна и самой наклонной. То есть, если прямая а, принадлежащая плоскости 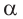перпендикулярна прямой ВС в точке С, то она перпендикулярна и прямой АС.

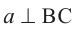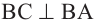Краткая запись: если и , то .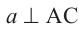

Для данной теоремы верна и обратная теорема.

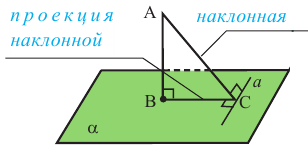
Обратная теорема. Если прямая, лежащая в плоскости перпендикулярна

наклонной, то она перпендикулярна и её проекции.

То есть, если прямая а, лежащая в плоскости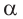, перпендикулярна прямой

АС в точке С , то она перпендикулярна и ВС.

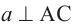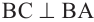Краткая запись: если и , то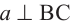

Докажем теорему.

Дано: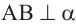

АС наклонная, проведённая к плоскости отрезок ВС - проекция наклонной АС.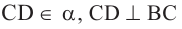

Доказать: СО АС

Пример 1. Длина перпендикуляра СМ, восстановленного к вершине прямого угла прямоугольного треугольника АВС равна 7,2 единицам, а длина высоты, проведённой к гипотенузе равна 9,6 единицам. Найдите расстояние от точки М до гипотенузы.

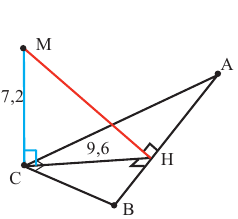
Решение: по теореме о трёх перпендикулярах, т.к. 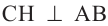, то 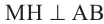. Расстояние от точки М до гипотенузы равно длине отрезка МН. Из 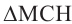по теореме Пифагора имеем: 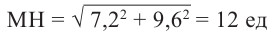. Пример 2. Длина перпендикуляра, восстановленного к плоскости треугольника из вершины большего угла равна 15 ед. Найдите расстояние от вершины перпендикуляра до большей стороны, если стороны треугольника равны 10, 17 и 21 ед.

Решение: если 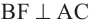, то 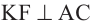. То есть, надо найти длину отрезка КF.

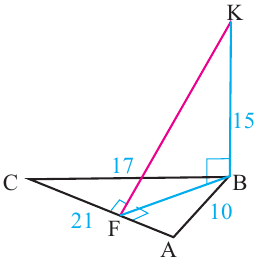
По формуле Герона найдём площадь .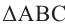

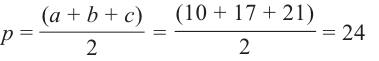
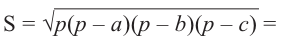
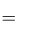
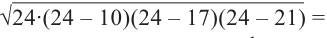
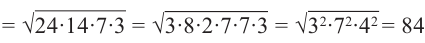
С другой стороны, .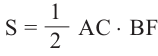

Отсюда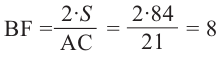

Так как отрезок КВ перпендикулярен ВР, то 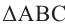прямоугольный.

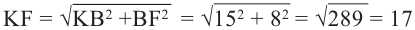
Угол между двумя плоскостями. Двугранный угол

Взаимное расположение плоскостей .

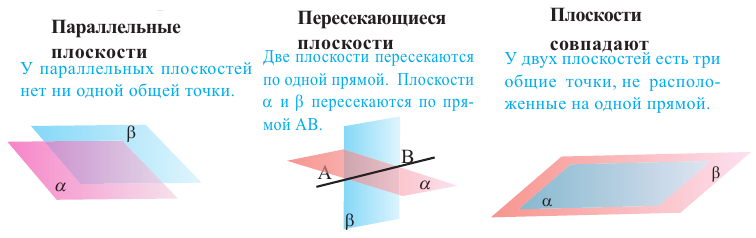
Угол, образованный двумя полуплоскостями и имеющий общую границу называется двугранным углом. Полуплоскости называются гранями, их общая граница называется ребром. При пересечении двух плоскостей образуется 4 двугранных угла. Если, из любой точки на ребре двугранного угла, в каждую полуплоскость провести перпендикулярные лучи, то они образуют угол, который называется линейным углом двугранного угла.

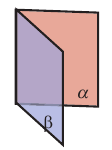
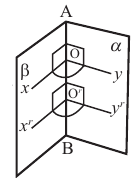
Двугранный угол измеряется его линейным углом. Градусной мерой двугранного угла называется градусная мера его линейного угла. Все линейные углы двугранного угла при параллельном переносе совпадают, то есть они равны (прямые, перпендикулярные одной и той же прямой параллельны).

Значение линейного угла не зависит от места расположения его вершины.

Градусная мера двугранного угла лежит в пределах от 0° до 180°.

Пример 1. На грани двугранного угла, градусная мера которого равна 30°, взята точка, удалённая от другой грани на расстояние а. Найдите расстояние от этой точки до ребра двугранного угла.

Решение. Пусть дана точка 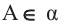. Проведём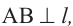 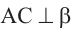. По теореме о трёх перпендикулярах 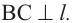Значит, 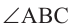линейный угол и 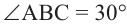. В прямоугольном треугольнике ABC катет, лежащий напротив в угла 30° равен половине гипотенузы: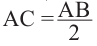

Отсюда: .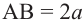

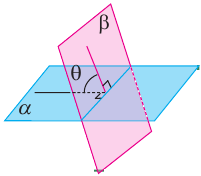
Углом между двумя пересекающимися плоскостями принято считать меньший из двух углов, образованных при пересечении плоскостей. На рисунке, говоря об угле между плоскостями 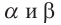имеют ввиду угол 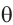, образованный перпендикулярными прямыми, опущенными на линию пересечения плоскостей.

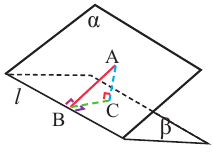
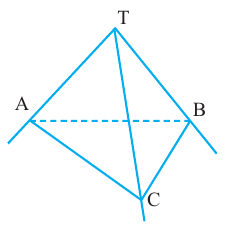
Изобразим треугольник ABC и лучи ТА, ТВ и ТС, из точки Т вне плоскости треугольника. Точка Т является общей вершиной для углов , 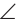ATB и 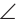BTC, не расположенных в одной плоскости. Полученная фигура называется трёхгранным углом. Плоские углы называются гранями, стороны называются рёбрами, общая вершина называется вершиной трёхгранного угла. Каждое ребро, в свою очередь, также является ребром двугранного угла.

Теорема 1. Сумма плоских углов трёхгранного угла меньше 360°.

Теорема 2. Плоский угол трёхгранного угла меньше суммы двух други плоских углов.

Пример 2. Существует ли трёхгранный угол с плоскими углами:

а)130°, 100°, 140° ; б) 70°, 80°, 100°?

Решение:

а) нет, так как 130°+ 100°+ 140°= 370° > 360°

б)да, так как 70°+80°+ 100° < 360° и каждый плоский угол меньше суммы двух других плоских углов.

• Заказать решение задач по высшей математике

Перпендикулярные плоскости

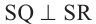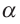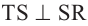Определение. Если двугранный угол, образованный при пересечении двух плоскостей прямой, то плоскости называются перпендикулярными плоскостями. на плоскости и на плоскост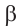и и

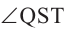равен линейному углу двугранного угла с ребром и граням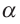и и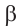. Если 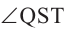прямой, то .

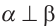Теорема (признак перпендикулярности плоскостей). Если плоскость проходит через прямую перпендикулярную другой плоскости, то эти плоскости перпендикулярны.

Дано: Прямая АВ перпендикуляр, опущенный из точки А на плоскость 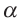. Точка С не лежит в плоскости .

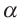Доказать: Плоскость 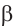, проходящая через точки А, В, С перпендикулярна плоскости .

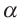Доказательство: Обозначим прямую, по которой пересекаются плоскост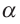и и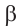 через АО . Эта прямая является ребром двугранного угла, образованного данными плоскостями. В плоскости 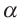проведём линию АЕ перпендикулярную АО. Так как 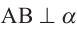, то линия АВ перпендикулярна любой прямой пересекающей её в точке А.

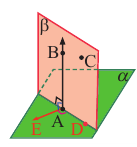
То есть, 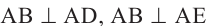. Угол 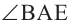является линейным углом двугранного угла. А так как 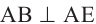, то двугранный угол прямой. Таким образом 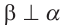. Теорема доказана. Можно смоделировать любую плоскость, проходящую через прямую 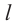вращением плоскости 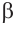вокруг прямой.

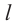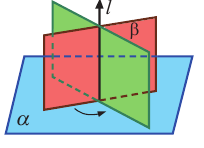
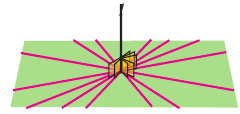
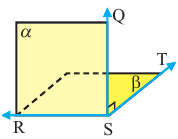
Пример прикладного задании. Примером перпендикулярных плоскостей служит крутящиеся двери, которые обычно устанавливают при входе в отелях или торговых центрах. Из схемы видно, что прямая ST перпендикулярна полу и дверь крутиться вокруг этой прямой. При этом плоскости STU, STR также перпендикулярны плоскости пола RTU.

Параллельные плоскости

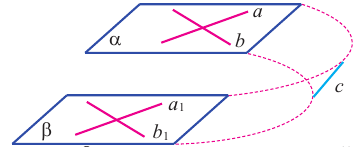
Теорема 1. (Признак параллельности плоскостей) Если две пересекающиеся прямые одной плоскости соответственно параллельны двум пересекающимся прямым другой плоскости, то эти плоскости параллельны.

Доказательство: Пусть, две пересекающиеся прямые а и b лежат в плоскости 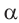, a две пересекающиеся прямые 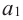и 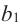расположены в плоскост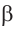и и 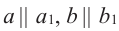. Покажем, что .

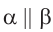Предположим обратное. Пусть, плоскост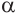и и 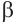пересекаются по прямой с. По признаку параллельности прямой и плоскости а || с и b || с. Отсюда следует, что прямая с параллельна каждой из пересекающих её прямых a и b. А это невозможно. Получили противоречие. Значит, .

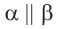Теорема 2. Если две параллельные плоскости пересекаются третьей плоскостью, то линии пересечения плоскостей параллельны.

То есть, если параллельные плоскости 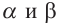пересекаются плоскостью 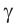, то линии пересечения 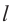и m параллельны. Краткая запись: если плоскость 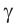пересекает плоскости .

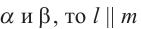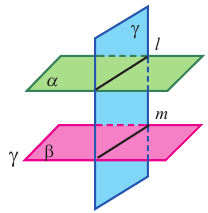
Пример прикладного задания. Плоскости ABG и DCF прямоугольного параллелепипеда параллельны. Какие плоскости образуют рёбра, пересекая эти плоскости?

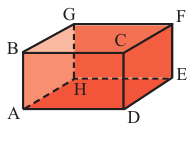
Решение:

1. Плоскость ABC, пересекая параллельные плоскости ABG и DCF, образует параллельные рёбра АВ и CD: .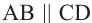

2. Плоскость HGF, пересекая плоскости ABG и DCF образует параллельные рёбра GH и FE: GH || FE.

Доказательство теоремы:

Дано: 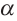|| . Пусть прямая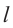является линией пересечения плоскосте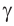й и 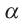, прямая m является линией пересечения плоскосте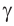й и .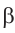

Доказать: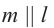

Доказательство: так как прямые m и 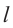лежат в плоскости 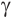, то они не являются скрещивающимися, а также не пересекающимися, так как в этом случае плоскост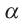и и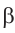 имели бы общую точку. На самом деле, если прямые 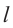и m пересекаются в какой-либо точке, то эта точка должна принадлежать как прямой 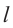, то есть лежать в плоскости 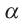, так и прямой m, то есть в плоскости 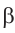. Однако, плоскост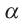и и 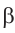параллельны, а значит они не имеют ни одной общей точки. Значит m || 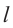. Теорема доказана.

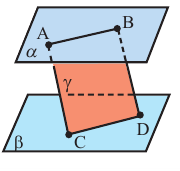
Теорема 3. Отрезки параллельных прямых, расположенных между двумя параллельными плоскостями равны (докажите самостоятельно).

Теорема 4. Две прямые перпендикулярные одной плоскости параллельны.

Дано: плоскость .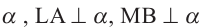

Докажите: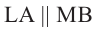

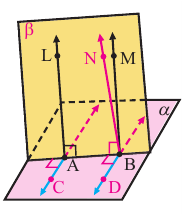
Для доказательства теоремы проведём прямую ВN, параллельно прямой LА. Надо показать, что прямые ВN и ВМ совпадают. Докажите теорему, выполнив следующее. / /с /р/

1. Покажите, что 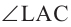является линейным углом прямого двугранного угла между плоскостями .
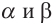2. Покажите, что если одна из двух параллельных прямых перпендикулярна третьей, то другая прямая также перпендикулярна этой прямой, то есть из условия 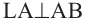следует, что .
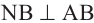3. На плоскости 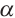проведите 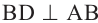. Используя то, что двугранный угол между плоскостями 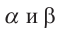прямой, покажите, что .
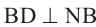4. Покажите, что перпендикуляр МВ к плоскости 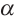восстановленный из точки В является единственным.

Теорема 5. Две плоскости, перпендикулярные одной прямой параллельны. Доказательство теоремы:

Дано: .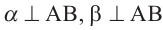

Докажите:

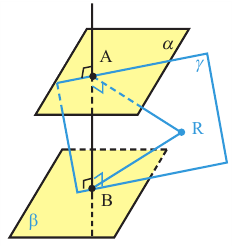
Доказательство: Допустим обратное. Пусть, точка R принадлежит прямой пересечения плоскостей 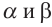. Плоскость 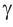, проходит через точки А, В и R. Для плоскости 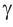имеем: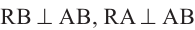. Однако, прямые перпендикулярные одной и той же прямой в плоскости должны быть параллельны. Значит, предположение, что плоскости 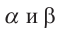пересекаются, ложно. Эти плоскости параллельны: . Теорема доказана.

Пример прикладного задании. Керим делает из картона модель автомобиля. Ось DG, соединяющая колёса автомобиля должна быть перпендикулярна. По какой линии должна быть перпендикулярна ось, чтобы колёса были параллельны?

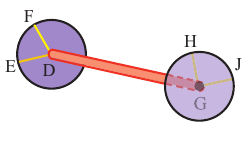
Решение: если ось DG перпендикулярна пересекающимся в плоскости ЕFD прямым ЕD и FD и пересекающимся в плоскости НGJ прямым НG и GJ то Керим может быть уверен, что колёса параллельны.

Теорема 6. Прямая перпендикулярная одной из двух параллельных плоскостей, перпендикулярна и другой плоскости.

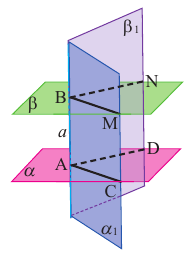
Доказательство. Пусть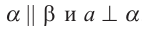. Плоскост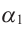и и 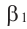проходящие через прямую а пересекаются с плоскостями 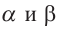по параллельным прямым : , . Так как 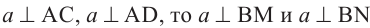. По признаку перпендикулярности прямой и плоскости 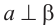. Теорема доказана.

Расстояние между двумя параллельными плоскостями

Расстояние между двумя плоскостями, равно длине перпендикуляра, опущенного из любой точки одной плоскости до другой.

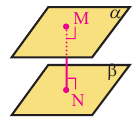
Расстояние между двумя скрещивающимися прямыми

Через каждую из двух скрещивающихся прямых проходит плоскость, параллельная другой прямой. Например, проведём через прямую b плоскость, параллельную прямой а. Для этого, проведем прямую 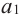, которая пересекает прямую b ( так, чтобы она прошла параллельно прямой а.

Плоскость, проходящая через прямые 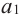и b, параллельна прямой а. Расстояние, от любой точки прямой а до этой плоскости, равно расстоянию между скрещивающимися прямыми а и b. Если 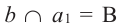, то отрезок АВ, перпендикулярный плоскости 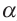, является общим перпендикуляром для скрещивающихся прямых а и b.

Проекции

Решение задач.

Для уточнения форм, при изготовлении хозяйственных товаров, промышленного оборудования, машин и механизмов, используют рисунки с различных сторон.

Для изображении фигур в пространстве используют параллельное проецирование. Возьмём любую прямую 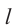, пересекающую плоскость 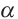. Тогда точка А' будет являться точкой пересечения плоскости с прямой, содержащей точку А при переносе этой точки параллельно прямой 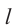. По аналогичному правилу можно получить изображение каждой точки фигуры.

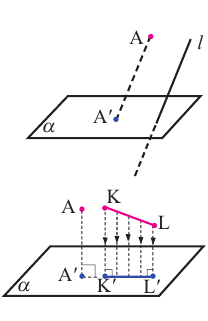
В этом случае параллельные отрезки фигуры изображаются параллельными отрезками и сохраняется их отношения. В частном случае, если прямая 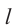перпендикулярна плоскости 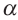, то полученное изображение фигуры является ортогональной проекций. На рисунке показан пример ортогональной проекции различных положений отрезка как по горизонтали, так и по вертикали.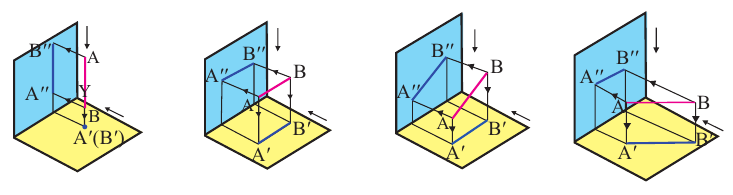

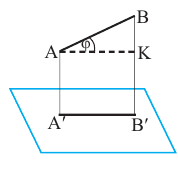
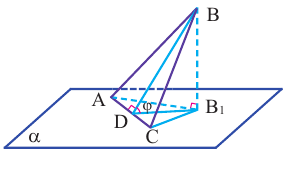
Для нахождения длины проекции отрезка используют соотношение 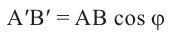. Найдём площадь ортогональной проекции 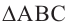на плоскость 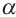, если угол 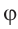является углом между и плоскостью треугольника и плоскостью, проходящей через сторону АС.

Если 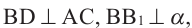то по теореме о трёх перпендикулярах .

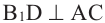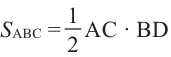Из ,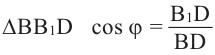

Зная , что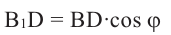

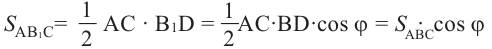
В общем случае, если угол 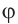- угол между плоскостью многоугольника и плоскостью проекции, то справедлива формула 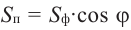. Здесь 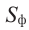- площадь многоугольника, 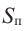- площадь ортогональной проекции.

Пример. Прямоугольный параллелепипед освещен сверху. Начертите проекции заданных отрезков на плоскость основания.

а) ВD б) NB в) ВЕ г) ВХ

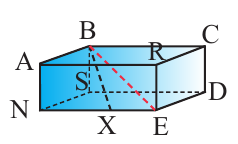
Проекции на плоскость основания:

а)Проекции ВD соответствует SD.

в)Проекции ВЕ соответствует SЕ.

б)Проекции NB cooтвeтcтвyeт NS.

г)Проекции ВХ соответствует SХ.