
Точка и прямая в начертательной геометрии с примерами
Содержание:
Для полного выявления наружных и внутренних форм деталей и их соединений вводят три и более плоскости проекций.
Введем в систему плоскостей 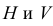
Три взаимно-перпендикулярные плоскости делят пространство на восемь частей, восемь октантов (рис. 3.2) (от лат. octo - восемь).
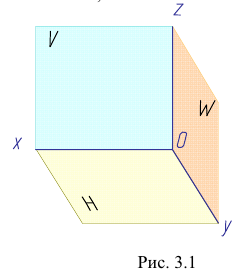
В нашей стране принята европейская система расположения проекций. Ось х направлена от начала координат влево, у - вперед (к нам), z - вверх. Обратные направления координатных осей считаются отрицательными.
Чертеж точки
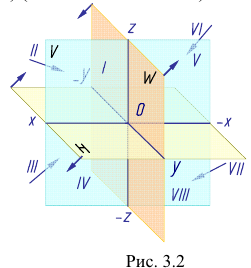
Опустим из точки А проецирующие лучи (перпендикуляры) до пересечения с плоскостями проекций Н, V и W. Точки пересечения перпендикуляров с плоскостями проекций - это проекции точки на каждую из плоскостей проекций:
- а - горизонтальная;
- а‘ - фронтальная;
- а " - профильная.
Данное наглядное изображение тонки в системе плоскостей Н, V и W (рис. 3.3) неудобно для черчения из-за сложности. Преобразуем его так, чтобы горизонтальная и профильная плоскости проекций совпали с фронтальной плоскостью проекций, образуя одну плоскость чертежа (рис. 3.4).
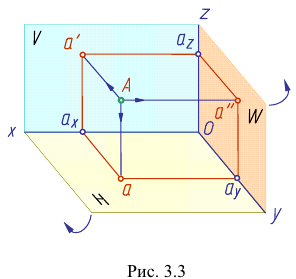
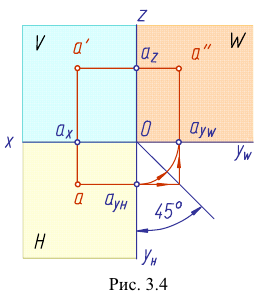
Это преобразование осуществляют путем поворота вокруг оси х плоскости Н на угол 90° вниз и плоскости W на угол 90° вправо вокруг оси z. В результате указанного совмещения плоскостей получаем чертеж, называемый эпюр Монжа (от франц, 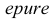 - чертеж, проект).
- чертеж, проект).
На эпюре мы не можем показать пространственную картину расположения плоскостей проекций и точки. Но эпюр обеспечивает точность изображений при значительной простоте построений.
В дальнейшем эпюр Монжа, а также проекционные чертежи будем называть одним словом - чертеж (или комплексный чертеж).
Горизонтальная и фронтальная проекции точки 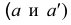 расположены на одном перпендикуляре к оси
расположены на одном перпендикуляре к оси 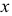 - на линии связи
- на линии связи 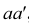 , фронтальная и профильная проекции
, фронтальная и профильная проекции 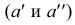 - на одном перпендикуляре к оси z - на линии связи
- на одном перпендикуляре к оси z - на линии связи 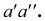 Построение профильной проекции точки по ее фронтальной и горизонтальной проекциям показано на рис. 3.4. При построении можно использовать дугу окружности с центром в точке О, или биссектрису угла
Построение профильной проекции точки по ее фронтальной и горизонтальной проекциям показано на рис. 3.4. При построении можно использовать дугу окружности с центром в точке О, или биссектрису угла 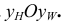 Первый способ более точный.
Первый способ более точный.
Таким образом, на комплексном чертеже трех ортогональных проекций точки
- две проекции находятся на одной линии связи;
- линии связи перпендикулярны осям проекций;
- две проекции точки определяют положение се третьей проекции;
- две проекции точки определяют ее положение в пространстве.
Положение точки в пространстве задается при помощи трех се координат (абсциссы 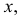 ординаты
ординаты 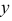 и аппликаты
и аппликаты 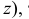 то есть трех чисел, выражающих расстояние от этой точки до координатных плоскостей проекций. Запись координат точки производят в такой форме: А (х, у, z). Положение точки на плоскости определяют две координаты: а(х,у); a'(x,z); a"(y,z).
то есть трех чисел, выражающих расстояние от этой точки до координатных плоскостей проекций. Запись координат точки производят в такой форме: А (х, у, z). Положение точки на плоскости определяют две координаты: а(х,у); a'(x,z); a"(y,z).
По отношению к плоскостям проекций точка может занимать как общее (точка А), так и частные (точки В и С) положения (рис. 3.5). Если точка лежит в плоскости проекций, то две ее проекции лежат на осях проекций (точка В). У такой точки одна ее координата равна нулю. Если точка принадлежит одновременно двум плоскостям проекций (точка С), то она лежит на оси проекций. Две ее проекции совпадают, а третья совпадает с точкой О — началом координат. В атом случае две ее координаты равны нулю. Если точка принадлежит трем плоскостям проекций, то она расположена в начале координат.
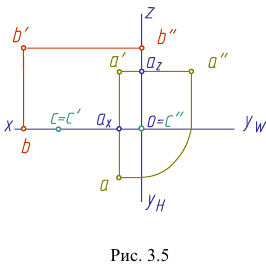
Таким образом, величины отрезков линий связи на чертеже определяют численное расстояние проецируемой точки до плоскости проекций. Отрезок 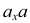 указывает, на каком расстоянии (глубине) расположена точка от фронтальной плоскости проекций, отрезок
указывает, на каком расстоянии (глубине) расположена точка от фронтальной плоскости проекций, отрезок 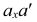 - расстояние (высоту) от точки до горизонтальной плоскости проекций и отрезок
- расстояние (высоту) от точки до горизонтальной плоскости проекций и отрезок 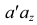 . - расстояние от точки до профильной плоскости проекций (рис. 3.4).
. - расстояние от точки до профильной плоскости проекций (рис. 3.4).
Взаимное положение двух точек. Условия видимости на чертеже
Рассмотрим чертеж модели, изображенной на рис. 3.6. Проекции некоторых точек совпадают, так как они расположены на одной проецирующей прямой. Например, на горизонтальной плоскости совпали проекции а и b вершин А и В - они лежат на одной горизонтально - проецирующей прямой. На фронтальной плоскости совпали проекции с ' и d ' вершин С и D - они лежат на одной фронтально-проецирующей прямой.
Точки, лежащие на одной проецирующей прямой, называют конкурирующими. А и В - горизонтально-конкурирующие точки, а С и D - фронтально-конкурирующие точки и т.д.
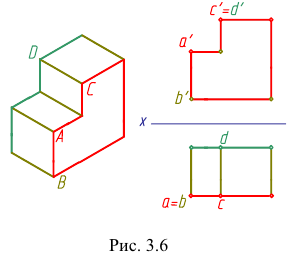
Ясно, что если две точки лежат на одной проецирующей прямой, то одна из них закрывает другую. Как определить, какая из них будет видимая и какая невидимая?
Из двух горизонтально- конкурирующих точек на горизонтальной плоскости видима та, которая расположена в пространстве выше. Анализируя положение фронтальных проекций точек (рис. 3.7), определяем, что точка А имеет большую координату z, чем точка В.
Следовательно, точка А расположена выше точки В и при проецировании на горизонтальную плоскость проекций закроет точку В. Точка А на горизонтальной плоскости видима, точка В - невидима. На фронтальной плоскости они обе видимы.
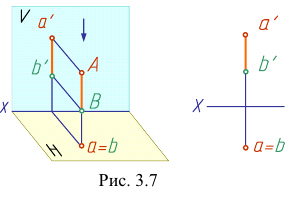
Из двух фронтально- конкурирующих точек на фронтальной плоскости проекций будет видима та, которая расположена ближе к наблюдателю, стоящему лицом к фронтальной плоскости проекций (рис. 3.8).
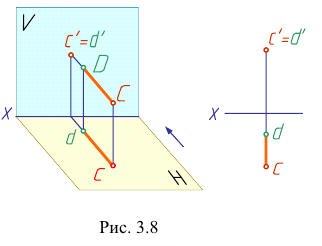
Какая из точек ближе к наблюдателю, можно определить по горизонтальным проекциям. Например, сравнивая горизонтальные проекции точек D и С , заключаем, что на фронтальной плоскости проекций видима точка С, а точка D - невидима, так как 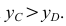
Из двух профильно-конкурирующих точек на профильной плоскости проекций будет видима та точка, которая расположена левее.
Итак, если на чертеже одноименные проекции точек не совпадают или совпадает только одна пара проекций, то такие точки в пространстве не совпадают, а удалены друг от друга на определенное расстояние (рис. 3.7, 3.8).
Чертёж отрезка прямой. Прямые частного положения
Наглядное изображение отрезка АВ прямой и его ортогональное проецирование на плоскость Р показано на рис. 3.9. Рассмотрим ортогональное проецирование отрезка АВ с учетом свойств параллельного проецирования. Проецирующие прямые 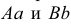 образуют проецирующую плоскость
образуют проецирующую плоскость 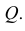 Линия пересечения плоскостей
Линия пересечения плоскостей 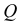 и Р проходит через проекции а и b точек А и В на плоскости проекций Р. Эта линия и является единственной проекцией прямой АВ на плоскости проекций Р.
и Р проходит через проекции а и b точек А и В на плоскости проекций Р. Эта линия и является единственной проекцией прямой АВ на плоскости проекций Р.
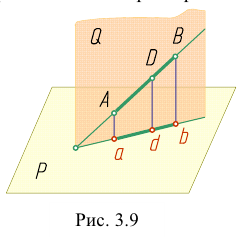
Наглядное изображение проецирования отрезка АВ прямой на две плоскости проекций в системе Н,V показано на рис. 3.10, чертеж - на рис. 3.1 I.
Если какая-либо точка принадлежит прямой, то ее проекция принадлежит проекции прямой. Например, точка D (рис. 3.9) принадлежит прямой АВ, ее проекции - проекциям прямой.
Относительно плоскостей проекции прямая может занимать различные положения:
- - не параллельное ни одной из плоскостей проекций
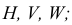
- - параллельное одной из плоскостей проекций (прямая может и принадлежать этой плоскости);
- - параллельное двум плоскостям проекций, то есть перпендикулярное третьей.
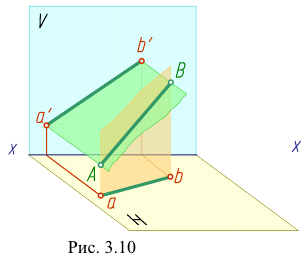
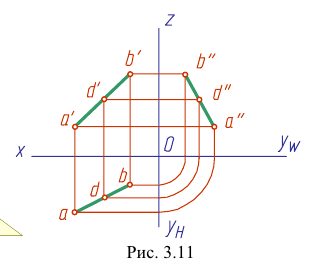
Прямую, не параллельную ни одной из плоскостей проекций, называют прямой общего положения (рис. 3.9 — 3.11).
Прямую, параллельную одной из плоскостей проекций или двум плоскостям проекций (то есть перпендикулярную третьей), называют прямой частного положения.
На рис. 3.12 - 3.14 приведены наглядные изображения и чертежи прямых частного положения - прямых, параллельных плоскостям проекций. Такие прямые называют прямыми уровня.
Различают три вида таких прямых.
Прямая АВ параллельна плоскости Н
Такую прямую называют «горизонтальной прямой» (рис. 3.12). Фронтальная проекция прямой 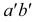 параллельна оси
параллельна оси 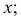 профильная проекция
профильная проекция 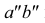 параллельна оси
параллельна оси 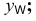 длина горизонтальной проекции отрезка равна длине самого отрезка
длина горизонтальной проекции отрезка равна длине самого отрезка 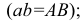 угол
угол 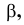 образованный горизонтальной проекцией и осью проекции
образованный горизонтальной проекцией и осью проекции 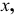 равен углу наклона прямой к фронтальной плоскости проекций; угол
равен углу наклона прямой к фронтальной плоскости проекций; угол 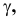 образованный горизонтальной проекцией и осью проекции равен углу наклона прямой к профильной плоскости проекций:
образованный горизонтальной проекцией и осью проекции равен углу наклона прямой к профильной плоскости проекций:
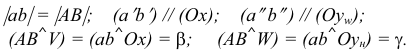
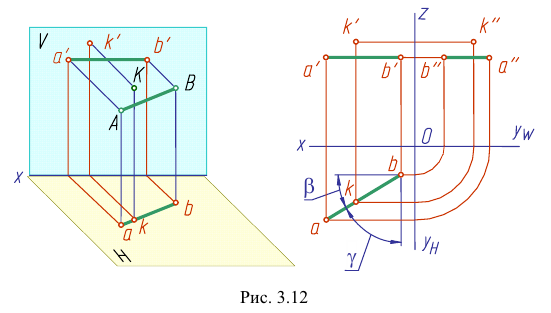
Прямая CD параллельна плоскости V
Такую прямую называют «фронтальной прямой» (рис. 3.13).
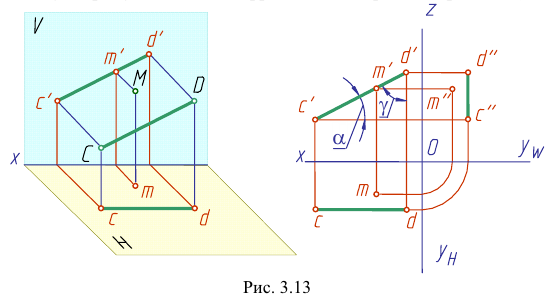
Горизонтальная проекция прямой cd параллельна оси х; профильная проекция 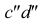 параллельна оси z; длина фронтальной проекции отрезка равна длине самого отрезка
параллельна оси z; длина фронтальной проекции отрезка равна длине самого отрезка 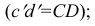 угол
угол 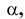 образованный фронтальной проекцией и осью проекций х, равен углу наклона прямой к горизонтальной плоскости проекций; угол
образованный фронтальной проекцией и осью проекций х, равен углу наклона прямой к горизонтальной плоскости проекций; угол 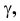 образованный фронтальной проекцией и осью z, равен углу наклона прямой к профильной плоскости проекций:
образованный фронтальной проекцией и осью z, равен углу наклона прямой к профильной плоскости проекций:
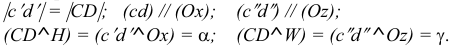
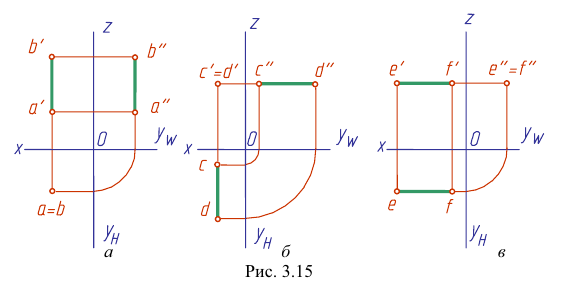
Прямая EF параллельна плоскости IF
Такая прямая носит название «профильная прямая» (рис. 3.14).
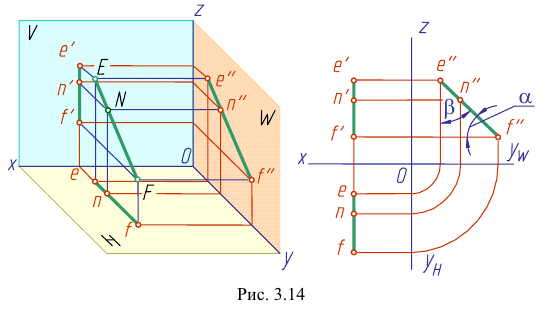
Горизонтальная проекция прямой 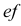 параллельна оси
параллельна оси 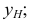 фронтальная проекция
фронтальная проекция 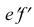 параллельна оси
параллельна оси 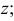 длина профильной проекции отрезка равна длине самого отрезка
длина профильной проекции отрезка равна длине самого отрезка 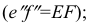 углы
углы 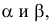 образованные профильной проекцией с осями
образованные профильной проекцией с осями 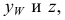 равны углам наклона прямой к горизонтальной и фронтальной плоскостям проекций соответственно:
равны углам наклона прямой к горизонтальной и фронтальной плоскостям проекций соответственно:
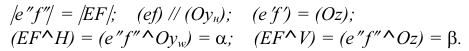
Следовательно, каждая линия уровня проецируется в истинную величину на ту плоскость проекции, которой она параллельна. На ту же плоскость проекций проецируются без искажения и углы, которые эта прямая образует с остальными двумя плоскостями проекций.
На рис. 3.15 приведены чертежи прямых, перпендикулярных плоскостям проекций. Такие прямые называются проецирующими прямыми. Различают три вида таких прямых.
Прямая АВ перпендикулярна плоскости Н
АВ - горизонтально-проецирующая прямая. Ее проекция 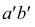 перпендикулярна оси х, проекция
перпендикулярна оси х, проекция 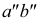 перпендикулярна оси
перпендикулярна оси 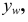 , проекции а и b совпадают (рис. 3.15, а):
, проекции а и b совпадают (рис. 3.15, а):
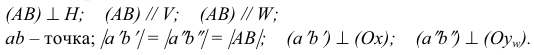
Прямая CD перпендикулярна плоскости V
CD - фронтально-проецирующая прямая. Ее проекция cd перпендикулярна оси х, проекция c"d“ перпендикулярна оси z, проекции с’ и d' совпадают (рис. 3.15, б):
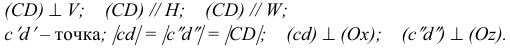
Прямая EF перпендикулярна плоскости W
EF - профильно-проецирующая прямая. Ее проекция 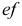 перпендикулярна оси
перпендикулярна оси 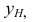 проекция
проекция 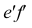 перпендикулярна оси z, проекции
перпендикулярна оси z, проекции 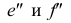 совпадают (рис. 3.15,
совпадают (рис. 3.15,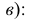
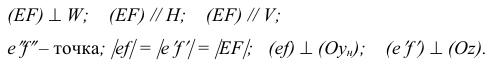
Из чертежа видно, что проецирующая прямая является вместе с тем и прямой двойного уровня, так как она параллельна одновременно двум другим плоскостям проекций
Следовательно, на две плоскости проекций проецирующие прямые проецируются без искажения, то есть в натуральную величину, а на третью - в точку.
Взаимное положение точки и прямой
Точка и прямая в пространстве могут быть различно расположены относительно друг друга и плоскости проекций.
Если точка в пространстве принадлежит прямой, то ее проекции принадлежат соответствующим проекциям этой прямой.
Если это положение нарушается, то точка данной прямой не принадлежит. На рис. 3.12 - 3.14 это положение показано на наглядных изображениях и чертежах прямых линий и точек.
Рассмотрим еще раз это положение на плоскостном чертеже (рис. 3.16). Точка F принадлежит прямой АВ, так как горизонтальная проекция 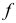 точки принадлежит горизонтальной проекции
точки принадлежит горизонтальной проекции 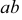 прямой, а фронтальная проекция
прямой, а фронтальная проекция 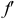 точки принадлежит фронтальной проекции
точки принадлежит фронтальной проекции 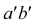 прямой:
прямой:
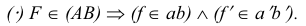
Точка С лежит над прямой АВ, точка D лежит под прямой АВ. точка Е лежит за прямой АВ.
Следы прямой
Точки пересечения прямой линии с плоскостями проекций называются следами прямой. На рис. 3.17. а точка М - горизонтальный след прямой, точка 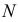 - фронтальный.
- фронтальный.
Горизонтальная проекция 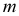 горизонтального следа прямой совпадает с самим следом - точкой
горизонтального следа прямой совпадает с самим следом - точкой 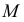 (рис. 3.17,
(рис. 3.17, 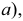 а фронтальная проекция этого следа
а фронтальная проекция этого следа 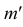 лежит на оси х. Фронтальная проекция
лежит на оси х. Фронтальная проекция 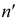 фронтального следа прямой совпадает с фронтальным следом - точкой N, а горизонтальная проекция
фронтального следа прямой совпадает с фронтальным следом - точкой N, а горизонтальная проекция 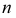 лежит на той же оси проекций.
лежит на той же оси проекций.
Чтобы построить на плоскостном чертеже горизонтальный след прямой (точки 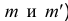 , надо продолжить фронтальную проекцию
, надо продолжить фронтальную проекцию 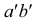 прямой до пересечения с осью х (точка
прямой до пересечения с осью х (точка 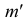 ). Затем через нес провести перпендикуляр к оси х до пересечения с продолжением горизонтальной проекции
). Затем через нес провести перпендикуляр к оси х до пересечения с продолжением горизонтальной проекции 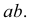 Точка
Точка 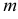 - горизонтальная проекция горизонтального следа.
- горизонтальная проекция горизонтального следа.
Для построения проекций фронтального следа (точек 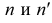 ) необходимо продолжить горизонтальную проекцию
) необходимо продолжить горизонтальную проекцию 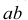 прямой до пересечения с осью х (точка
прямой до пересечения с осью х (точка 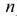 ). Затем через нес провести перпендикуляр к оси х до пересечения с продолжением фронтальной проекции
). Затем через нес провести перпендикуляр к оси х до пересечения с продолжением фронтальной проекции 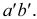 Точка
Точка 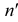 - фронтальная проекция фронтального следа. Построение проекций следов прямой показано на рис. 3.17, б.
- фронтальная проекция фронтального следа. Построение проекций следов прямой показано на рис. 3.17, б.
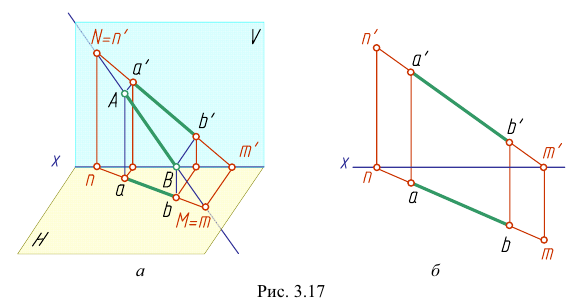
Прямая может пересекать и профильную плоскость проекций, то есть иметь профильный след. Этот след на профильной плоскости проекций совпадает со своей проекцией. Фронтальная и горизонтальная проекции его лежат соответственно на осях 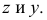
Взаимное положение двух прямых
Прямые в пространстве могут занимать различные взаимные положения:
- - пересекаться, то есть иметь одну общую точку;
- - быть параллельными, если точка пересечения прямых удалена в бесконечность;
- - скрещиваться, то есть не иметь обшей точки.
Пересекающиеся прямые
Если прямые пересекаются, то их одноименные проекции пересекаются между собой и точки пересечения проекций лежат на одной линии связи.
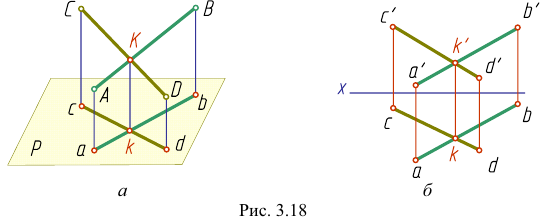
Наглядное изображение двух прямых АВ и CD, пересекающихся в точке К, приведено на рис. 3.18, 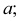 их чертеж в системе плоскостей
их чертеж в системе плоскостей 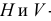 -на рис. 3.18, б.
-на рис. 3.18, б.
Если одна из прямых профильная, то чтобы ответить на вопрос, пересекаются ли прямые, следует построить их профильные проекции.
На рис. 3.19 все проекции точки 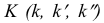 одновременно принадлежат проекциям прямой АВ и прямой CD. Это значит, что прямые АВ и CD пересекаются.
одновременно принадлежат проекциям прямой АВ и прямой CD. Это значит, что прямые АВ и CD пересекаются.
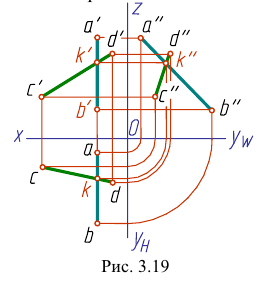
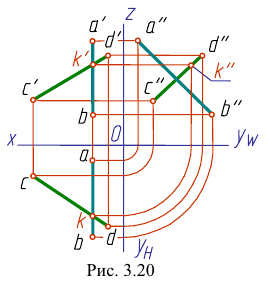
На рис. 3.20 профильная проекция 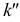 точки К принадлежит профильной проекции
точки К принадлежит профильной проекции 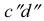 и не принадлежит профильной проекции
и не принадлежит профильной проекции 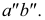
Это значит, что прямые АВ и CD не пересекаются, они скрещиваются.
Параллельные прямые
Если прямые в пространстве параллельны, то их одноименные проекции параллельны между собой. Действительно, на рис. 3.21 проецирующие плоскости 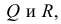 проведенные через параллельные прямые АВ и CD, параллельны между собой. С плоскостью проекций Р они пересекаются по параллельным прямым
проведенные через параллельные прямые АВ и CD, параллельны между собой. С плоскостью проекций Р они пересекаются по параллельным прямым 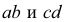 - проекциям прямых АВ и CD. Чертеж двух параллельных прямых общего положения приведен на рис. 3.22, чертежи параллельных прямых частного положения - на рис. 3.23:
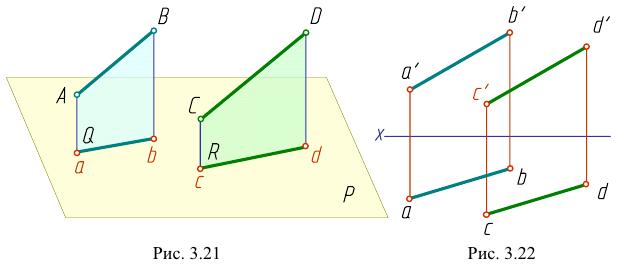
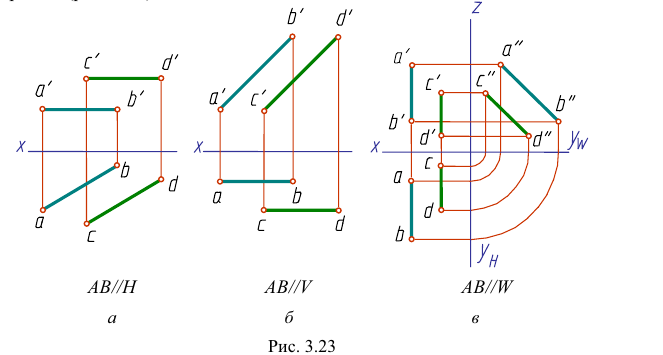
- проекциям прямых АВ и CD. Чертеж двух параллельных прямых общего положения приведен на рис. 3.22, чертежи параллельных прямых частного положения - на рис. 3.23:
- горизонтальных прямых (рис. 3.23, а);
- фронтальных прямых (рис. 3.23, б);
- профильных прямых (рис. 3.23,
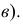
О параллельности прямых в пространстве можно судить по параллельности их одноименных проекций на двух плоскостях проекций.
При этом нужно учитывать некоторые условия.
Для прямых общего положения:
Если одноименные проекции прямых общего положения параллельны в системе двух любых плоскостей проекций, то прямые парал лельны (рис. 3.22).
Для прямых частного положения:
Если одноименные проекции прямых параллельны одной из осей проекций, то прямые параллельны при условии параллельности одноименных проекций на той плоскости проекций, которой параллельны прямые (рис. 3.23).
Скрещивающиеся прямые
Если прямые в пространстве нс пересекаются, а скрещиваются (рис. 3.24), то хотя на чертеже их одноименные проекции и пересекаются, но точки пересечения проекций не лежат на одной линии связи. Эти точки не являются общими для прямых.
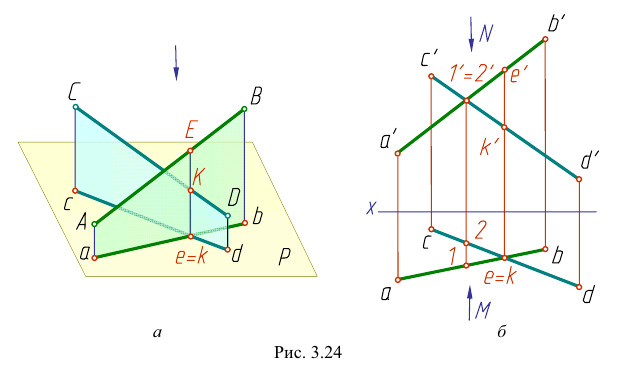
Сравнивая положение таких точек, определяют, какая из изображенных на чертеже прямых выше другой или ближе другой к наблюдателю. На рис. 3.24, а видно, что точка Е (принадлежащая прямой АВ) расположена выше точки К (принадлежащей прямой CD). При взгляде сверху по указанной стрелке точка Е закрывает точку К. Соответственно и на чертеже (рис. 3.24, б) фронтальная проекция е' расположена выше фронтальной проекции 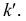 При взгляде сверху по стрелке N при проецировании на плоскость Н точка е закрывает точку
При взгляде сверху по стрелке N при проецировании на плоскость Н точка е закрывает точку 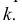 Прямая АВ проходит над прямой CD.
Прямая АВ проходит над прямой CD.
На плоскости V совпадают фронтальные проекции 1' и 2' точек прямых АВ и CD. При взгляде спереди по стрелке М видно, что точка 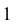 прямой АВ находится ближе к наблюдателю, и при проецировании на плоскость V точка
прямой АВ находится ближе к наблюдателю, и при проецировании на плоскость V точка 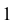 прямой АВ закрывает точку 2 прямой CD. Прямая АВ расположена ближе к наблюдателю. Рассмотренные точки являются конкурирующими, так как они лежат на одной линии связи, но на разных прямых.
прямой АВ закрывает точку 2 прямой CD. Прямая АВ расположена ближе к наблюдателю. Рассмотренные точки являются конкурирующими, так как они лежат на одной линии связи, но на разных прямых.
Проецирование плоских углов
Любой линейный угол образуется двумя пересекающимися прямыми. На плоскости проекций он проецируется в общем случае с искажением. Однако, если обе стороны угла параллельны какой-либо плоскости проекций, то на эту плоскость угол проецируется без искажения. Например, стороны угла АВС (рис. 3.25) параллельны горизонтальной плоскости Р. поэтому угол 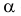 спроецировался на нее без изменений.
спроецировался на нее без изменений.
Исключение составляет прямой угол. Он проецируется в истинную величину даже тогда, когда лишь одна из его сторон параллельна плоскости проекций. Рассмотрим теорему о проецировании прямого угла.
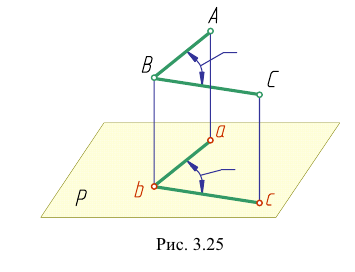
Теорема. Прямой угол проецируется в виде прямого угла, если одна из его сторон параллельна плоскости проекций, а вторая ей не пер пендикулярна. Пусть сторона DE прямого угла DEK параллельна плоскости Р, а сторона ЕК ей нс перпендикулярна (рис. 3.26). Требуется доказать, что его проекция - угол 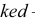 равна 90°:
равна 90°:
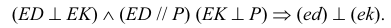
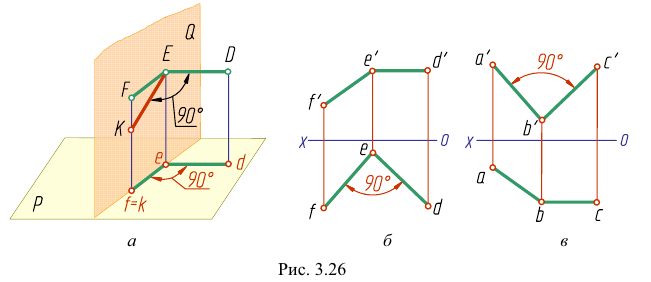
Доказательство. Пусть угол 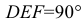 и расположен так, что обе его стороны параллельны плоскости Р(рис. 3.26, а). Тогда, как и всякая фигура, лежащая в плоскости, параллельной Р, данный угол спроецируется на Р без искажения, то есть его проекция
и расположен так, что обе его стороны параллельны плоскости Р(рис. 3.26, а). Тогда, как и всякая фигура, лежащая в плоскости, параллельной Р, данный угол спроецируется на Р без искажения, то есть его проекция 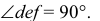
Через прямые EF и Ее проведем дополнительную плоскость 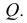 Плоскость
Плоскость 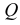 перпендикулярна плоскости Р.
перпендикулярна плоскости Р.
Возьмем на перпендикуляре 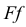 какую - либо точку К и соединим ее с Е. Угол DEK тоже прямой, так как
какую - либо точку К и соединим ее с Е. Угол DEK тоже прямой, так как 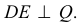 Проекция угла DEK совпадает с проекцией угла DEF, так как точки F и К лежат на одном перпендикуляре к плоскости Р. Таким образом
Проекция угла DEK совпадает с проекцией угла DEF, так как точки F и К лежат на одном перпендикуляре к плоскости Р. Таким образом
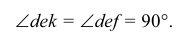
Но, как видно непосредственно из чертежа, только одна сторона DE угла DEK параллельна плоскости Р.
Вторая сторона его ЕК наклонна к плоскости Р.
Итак, для того чтобы прямой угол проецировался в натуральную величину, достаточно, чтобы одна его сторона была параллельна плоскости проекций (рис. 3.26, б, в).
Определение истинной величины отрезка прямой
Отрезки прямых общего положения не проецируются в истинную величину ни на одну из плоскостей проекций. Однако в ряде задач необходимо определить по чертежу длину отрезка прямой общего положения и углы наклона прямой к плоскостям проекций.
В этом случае используют способ построения прямоугольного треугольника.
Теорема. Истинная величина отрезка прямой общего положения равна гипотенузе прямоугольного треугольника, одним катетом которого является проекция отрезка на одну из плоскостей проекций, а другим - разность расстояний концов отрезка до этой же плоскости.
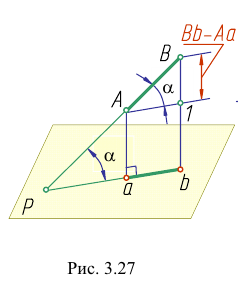
Доказательство. Из рис. 3.27 следует, что истинная величина отрезка АВ будет являться гипотенузой прямоугольного треугольника 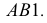 В этом треугольнике один катет равен проекции отрезка, а другой - разности расстояний концов отрезка до плоскости проекций.
В этом треугольнике один катет равен проекции отрезка, а другой - разности расстояний концов отрезка до плоскости проекций.
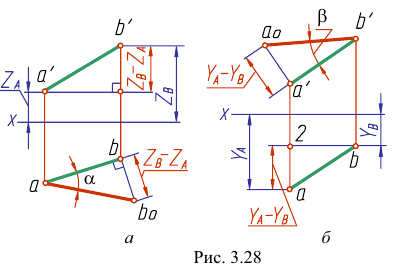
Определим истинную величину отрезка АВ и угол наклона его к плоскости Н (угол 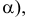 если известны две проекции отрезка (рис. 3.28, а).
если известны две проекции отрезка (рис. 3.28, а).
Построим прямоугольный треугольник, у которого одним катетом будет горизонтальная проекция отрезка, а вторым - разность расстояний концов отрезка до плоскости Н (разность z координат точек А и В). Истинная величина отрезка АВ равна гипотенузе abOt а угол наклона его к плоскости Н - угол 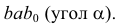
На рис. 3.28, 6 показано определение истинной величины отрезка АВ и угла наклона его к плоскости V- угла 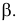
| Рекомендую подробно изучить предметы: |
| Ещё лекции с примерами решения и объяснением: |