Точечные оценки, свойства оценок - определение и вычисление с примерами решения

Содержание:

Точечные оценки:

Пусть случайная величина имеет неизвестную характеристику а. Такой характеристикой может быть, например, закон распределения, математическое ожидание, дисперсия, параметр закона распределения, вероятность определенного значения случайной величины и т.д. Пронаблюдаем случайную величину n раз и получим выборку из ее возможных значений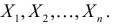

Существует два подхода к решению этой задачи. Можно по результатам наблюдений вычислить приближенное значение характеристики, а можно указать целый интервал ее значений, согласующихся с опытными данными. В первом случае говорят о точечной оценке, во втором – об интервальной.

Определение. Функция результатов наблюдений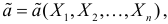

Для одной и той же характеристики можно предложить разные точечные оценки. Необходимо иметь критерии сравнения оценок, для суждения об их качестве. Оценка 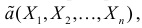как функция случайных результатов наблюдений 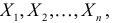сама является случайной величиной. Значения 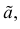найденные по разным сериям наблюдений, могут отличаться от истинного значения характеристики 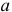в ту или другую сторону. Естественно потребовать, чтобы оценка систематически не завышала и не занижала оцениваемое значение, а с ростом числа наблюдений становилась более точной. Формализация названных требований приводит к следующим понятиям.

Определение. Оценка называется несмещенной, если ее математическое ожидание равно оцениваемой величине: 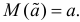В противном случае оценку называют смещенной.

Определение. Оценка называется состоятельной, если при увеличении числа наблюдений она сходится по вероятности к оцениваемой величине, т.е. для любого сколь угодно малого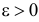

 

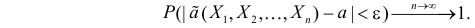
Если известно, что оценка 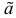несмещенная, то для ее состоятельности достаточно, чтобы

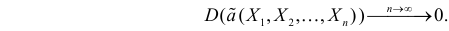
Последнее условие удобно для проверки. В качестве меры разброса значений оценки 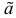относительно 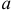можно рассматривать величину 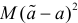Из двух оценок предпочтительней та, для которой эта величина меньше. Если оценка имеет наименьшую меру разброса среди всех оценок характеристики, построенных по 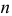наблюдениям, то оценку называют эффективной.

Следует отметить, что несмещенность и состоятельность являются желательными свойствами оценок, но не всегда разумно требовать наличия этих свойств у оценки. Например, может оказаться предпочтительней оценка хотя и обладающая небольшим смещением, но имеющая значительно меньший разброс значений, нежели несмещенная оценка. Более того, есть характеристики, для которых нет одновременно несмещенных и состоятельных оценок.

Оценки для математического ожидания и дисперсии

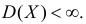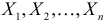Пусть случайная величина имеет неизвестные математическое ожидание и дисперсию, причем Если – результаты 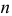независимых наблюдений случайной величины, то в качестве оценки для математического ожидания можно предложить среднее арифметическое наблюдаемых значений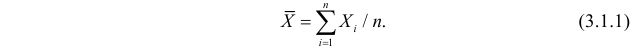 

Несмещенность такой оценки следует из равенств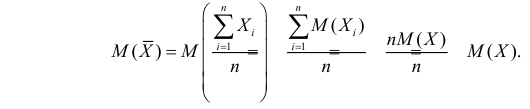

В силу независимости наблюдений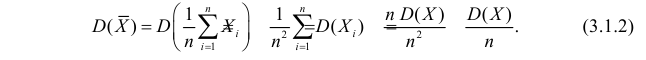 

При условии 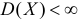имеем 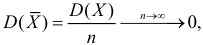что означает состоятельность оценки .

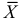Доказано, что для математического ожидания нормально распределенной случайной величины оценка 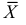еще и эффективна.

Оценка математического ожидания посредством среднего арифметического наблюдаемых значений наводит на мысль предложить в качестве оценки для дисперсии величину

 

Преобразуем величину 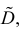обозначая для краткости 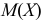через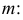

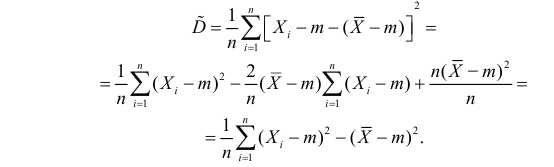
В силу (3.1.2) имеем 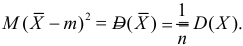Поэтому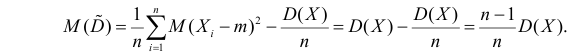 

Последняя запись означает, что оценка 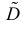имеет смещение. Она систематически занижает истинное значение дисперсии. Для получения несмещенной оценки введем поправку в виде множителя 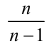и полученную оценку обозначим через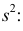

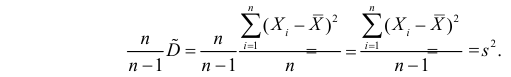
Величина

 

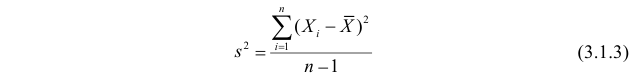
является несмещенной и состоятельной оценкой дисперсии.

Пример:

Оценить математическое ожидание и дисперсию случайной величины Х по результатам ее независимых наблюдений: 7, 3, 4, 8, 4, 6, 3.

Решение. По формулам (3.1.1) и (3.1.3) имеем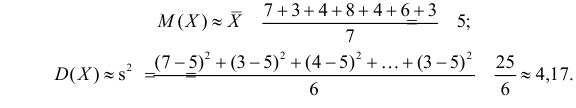 

Ответ.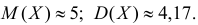 

Пример:

Данные 25 независимых наблюдений случайной величины представлены в сгруппированном виде:

Требуется оценить математическое ожидание и дисперсию этой случайной величины.

Решение. Представителем каждого интервала можно считать его середину. С учетом этого формулы (3.1.1) и (3.1.3) дают следующие оценки: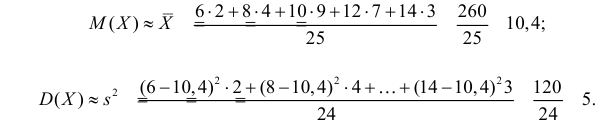

Ответ.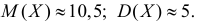  

Метод наибольшего правдоподобия для оценки параметров распределений

В теории вероятностей и ее приложениях часто приходится иметь дело с законами распределения, которые определяются некоторыми параметрами. В качестве примера можно назвать нормальный закон распределения 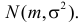Его параметры 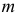и 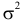имеют смысл математического ожидания и дисперсии соответственно. Их можно оценить с помощью 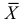и 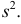В общем случае параметры законов распределения не всегда напрямую связаны со значениями числовых 179 характеристик. Поэтому практический интерес представляет следующая задача.

Пусть случайная величина Х имеет функцию распределения 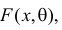причем тип функции распределения F известен, но неизвестно значение параметра 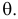По данным результатов наблюдений нужно оценить значение параметра. Параметр может быть и многомерным.

Продемонстрируем идею метода наибольшего правдоподобия на упрощенном примере. Пусть по результатам наблюдений, отмеченных на рис. 3.1.1 звездочками, нужно отдать предпочтение одной из двух функций плотности вероятност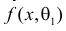и или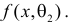  

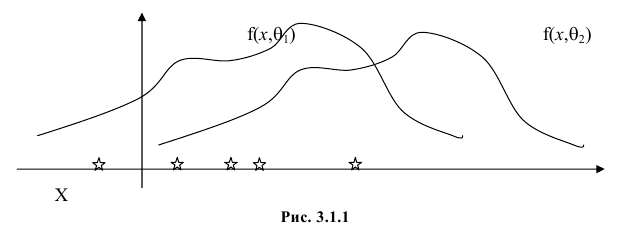
Из рисунка видно, что при значении параметра 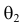такие результаты наблюдений маловероятны и вряд ли бы реализовались. При значении же 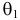эти результаты наблюдений вполне возможны. Поэтому значение параметра 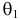более правдоподобно, чем значение 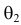. Такая аргументация позволяет сформулировать принцип наибольшего правдоподобия: в качестве оценки параметра выбирается то его значение, при котором данные результаты наблюдений наиболее вероятны.

Этот принцип приводит к следующему способу действий. Пусть закон распределения случайной величины Х зависит от неизвестного значения параметра 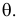Обозначим через 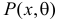для непрерывной случайной величины плотность вероятности в точке 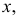а для дискретной случайной величины – вероятность того, что 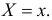Если в 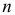независимых наблюдениях реализовались значения случайной величины 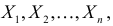то выражение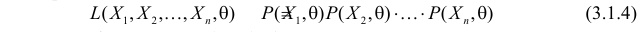

называют функцией правдоподобия. Величина 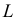зависит только от параметра 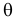при фиксированных результатах наблюдений 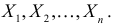При каждом значении параметра 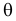функция равна вероятности именно тех значений дискретной случайной величины, которые получены в процессе наблюдений. Для непрерывной случайной величины равна плотности вероятности в точке выборочного пространства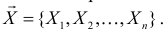

Сформулированный принцип предлагает в качестве оценки значения параметра выбрать такое 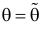при котором принимает наибольшее значение. Величина 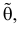 будучи функцией от результатов наблюдений  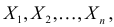называется оценкой наибольшего правдоподобия.

Во многих случаях, когда дифференцируема, оценка наибольшего правдоподобия находится как решение уравнения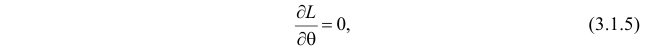 

которое следует из необходимого условия экстремума. Поскольку  достигает максимума при том же значении 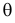, что и , то можно решать относительно 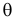эквивалентное уравнение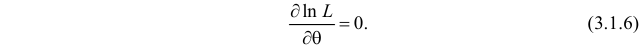

Это уравнение называют уравнением правдоподобия. Им пользоваться удобнее, чем уравнением (3.1.5), так как функция равна произведению, а – сумме, а дифференцировать проще.

Если параметров несколько (многомерный параметр), то следует взять частные производные от функции правдоподобия по всем параметрам, приравнять частные производные нулю и решить полученную систему уравнений.

Оценку, получаемую в результате поиска максимума функции правдоподобия, называют еще оценкой максимального правдоподобия.

Известно, что оценки максимального правдоподобия состоятельны. Кроме того, если для q существует эффективная оценка, то уравнение правдоподобия имеет единственное решение, совпадающее с этой оценкой. Оценка максимального правдоподобия может оказаться смещенной.

Метод моментов

Начальным моментом 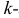го порядка случайной величины Х называется математическое ожидание 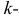й степени этой величины, т.е.  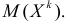Само математическое ожидание считается начальным моментом первого порядка.

Центральным моментом 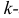го порядка называется  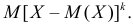Очевидно, что дисперсия – это центральный момент второго порядка. Если закон распределения случайной величины зависит от некоторых параметров, то от этих параметров зависят и моменты случайной величины.

Для оценки параметров распределения по методу моментов находят на основе опытных данных оценки моментов в количестве, равном числу оцениваемых параметров. Эти оценки приравнивают к соответствующим теоретическим моментам, величины которых выражены через параметры. Из полученной системы уравнений можно определить искомые оценки. 

Например, если Х имеет плотность распределения 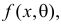то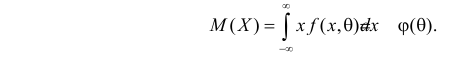 

Если воспользоваться величиной 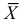как оценкой для 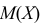на основе опытных данных, то оценкой 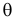по методу моментов будет решение уравнения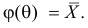 

Пример:

Найти оценку параметра показательного закона распределения по методу моментов.

Решение. Плотность вероятности показательного закона распределения имеет вид 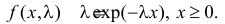Поэтому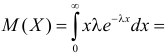 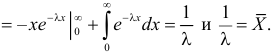 Откуда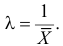 

Ответ.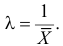 

Пример:

Пусть имеется простейший поток событий неизвестной интенсивности 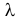. Для оценки параметра 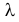проведено наблюдение потока и зарегистрированы  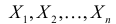– длительности последовательных интервалов времени между моментами наступления событий. Найти оценку для .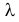

Решение. В простейшем потоке интервалы времени между последовательными моментами наступления событий потока имеют показательный закон распределения 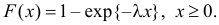Так как плотность вероятности показательного закона распределения равна  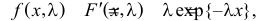то функция правдоподобия (3.1.4) имеет вид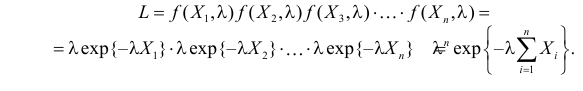

Тогда 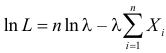  и уравнение правдоподобия  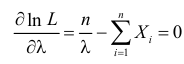имеет решение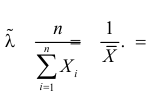 

При таком значении 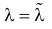функция правдоподобия действительно достигает наибольшего значения, так как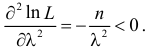 

Ответ.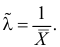 

Определение. Пусть 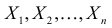 – результаты n независимых наблюдений случайной величины X. Если расставить эти результаты в порядке возрастания, то получится последовательность значений, которую называют вариационным рядом и обозначают: 

В этой записи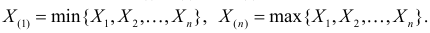  

Величины 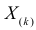называют порядковыми статистиками.

Пример:

Случайная величина Х имеет равномерное распределение на отрезке 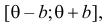где и неизвестны. Пусть 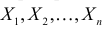 – результаты независимых наблюдений. Найти оценку параметра .

Решение. Функция плотности вероятности величины Х имеет вид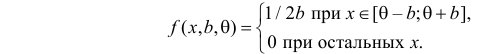

В этом случае функция правдоподобия 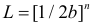от явно не зависит. Дифференцировать по такую функцию нельзя и нет возможности записать уравнение правдоподобия. Однако легко видеть, что  возрастает при уменьшении . Все результаты наблюдений лежат в 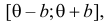 поэтому можно записать:

 

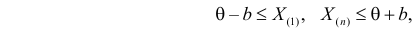
где 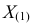– наименьший, а 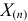– наибольший из результатов наблюдений. При минимально возможном  

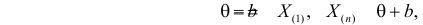
откуда 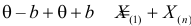или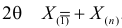

Оценкой наибольшего правдоподобия для параметра будет величина

Ответ.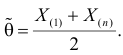 

Пример:

Случайная величина X имеет функцию распределения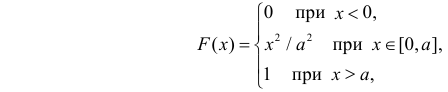

где 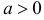неизвестный параметр.

Пусть 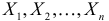 – результаты независимых наблюдений случайной величины X. Требуется найти оценку наибольшего правдоподобия для параметра 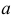и найти оценку для M(X).

Решение. Для построения функции правдоподобия найдем сначала функцию плотности вероятности

 

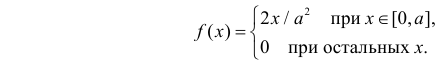
Тогда функция правдоподобия: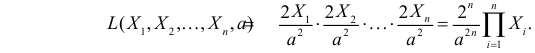 

Логарифмическая функция правдоподобия: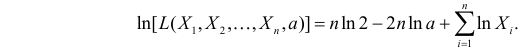 

Уравнение правдоподобия

 

не имеет решений. Критических точек нет. Наибольшее и наименьшее значения находятся на границе допустимых значений .

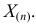По виду функции можно заключить, что значение тем больше, чем меньше величина . Но не может быть меньше Поэтому наиболее правдоподобное значение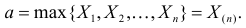

Так как 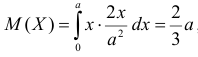, то оценкой наибольшего правдоподобия для 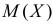будет величина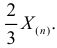
Ответ.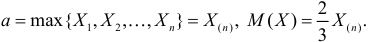

Пример:

Случайная величина Х имеет нормальный закон распределения 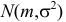c неизвестными параметрам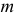и и 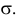 По результатам независимых наблюдений 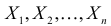найти наиболее правдоподобные значения этих параметров.

Решение. В соответствии с (3.1.4) функция правдоподобия имеет вид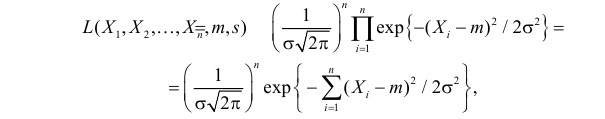 

а логарифмическая функция правдоподобия: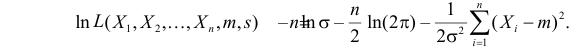 

Необходимые условия экстремума дают систему двух уравнений: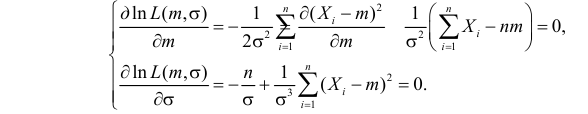 

Решения этой системы имеют вид: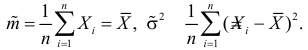 

Отметим, что обе оценки являются состоятельными, причем оценка для 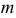несмещенная, а для 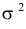смещенная (сравните с формулой (3.1.3)).

Ответ. 

Пример:

По данным эксперимента построен статистический ряд: 

Найти оценки математического ожидания, дисперсии и среднего квадратического отклонения случайной величины X.
Решение. 1) Число экспериментальных данных вычисляется по формуле:

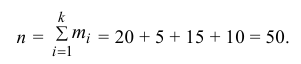
Значит, объем выборки n = 50.

2) Вычислим среднее арифметическое значение эксперимента:

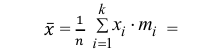
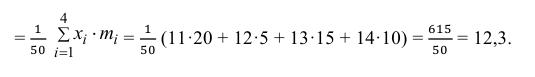
Значит, найдена оценка математического ожидания 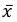= 12,3.

3) Вычислим исправленную выборочную дисперсию:

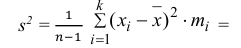
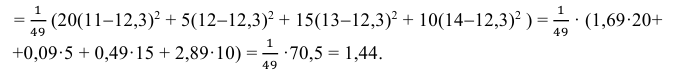
Значит, найдена оценка дисперсии: 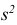 = 1,44.

5) Вычислим оценку среднего квадратического отклонения:

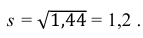
Ответ: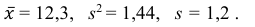

Пример:

По данным эксперимента построен статистический ряд: 

Найти оценки математического ожидания, дисперсии и среднего квадратического отклонения случайной величины X.
Решение. По формуле

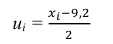
перейдем к условным вариантам: 

Для них произведем расчет точечных оценок параметров:

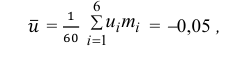
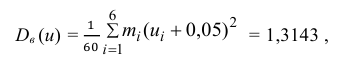
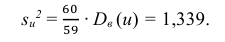
Следовательно, вычисляем искомые точечные оценки: 

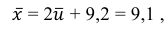
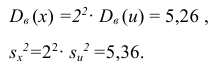
Ответ: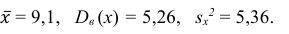 

Пример:

По данным эксперимента построен интервальный статистический ряд: 

Найти оценки математического ожидания, дисперсии и среднего квадратического отклонения.
Решение. 1) От интервального ряда перейдем к статистическому ряду, заменив интервалы их серединами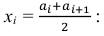  

2) Объем выборки вычислим по формуле:

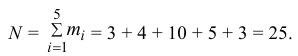
3) Вычислим среднее арифметическое значений эксперимента:

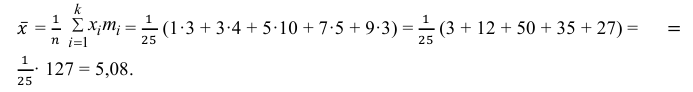
3) Вычислим исправленную выборочную дисперсию:

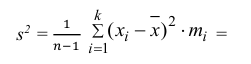
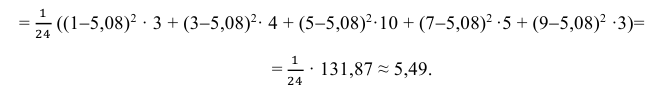
Можно было воспользоваться следующей формулой:

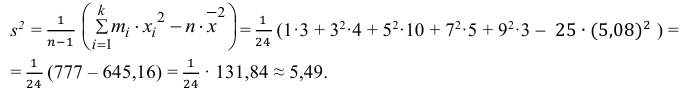
5)  Вычислим оценку среднего квадратического отклонения: 

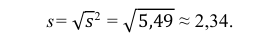
Ответ: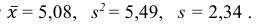 

Пример:

Найти доверительный интервал с надежностью 0,95 для оценки математического ожидания M(X) нормально распределенной случайной величины X, если известно среднее квадратическое отклонение σ = 2, оценка математического ожидания 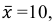 объем выборки n = 25.
 

Решение. Доверительный интервал для истинного математического ожидания с доверительной вероятностью 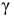 = 0,95 при известной дисперсии σ находится по формуле:

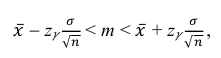
где m = M(X) – истинное математическое ожидание; 𝑥̅ − оценка M(X) по выборке; n – объем выборки; 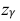 – находится по доверительной вероятности  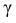= 0,95 из равенства:

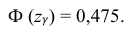
Из табл. П 2.2 приложения 2 находим: 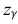 = 1,96. Следовательно, найден доверительный интервал для M(X): 

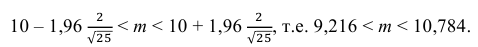
Ответ: (9,216 ; 10,784).

Пример:

По данным эксперимента построен статистический ряд: 

Найти доверительный интервал для математического ожидания M (X) с надежностью 0,95.
 

Решение. Воспользуемся формулой для доверительного интервала математического ожидания при неизвестной дисперсии:

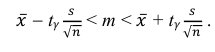
где n – объем выборки; 𝑥̅ оценка M(X);  s – оценка среднего квадратического отклонения; 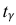  − находится по доверительной вероятности  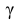= 0,95.

По числам 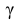 = 0,95 и n = 20 находим:  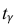= 2,093.
Теперь вычисляем оценки для M(X) и D(X):

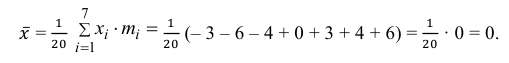
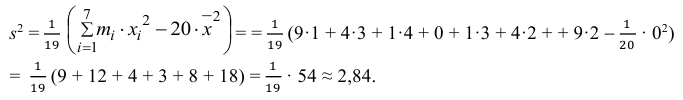
Следовательно, s ≈ 1,685. Поэтому искомый доверительный интервал математического ожидания задается формулой: 

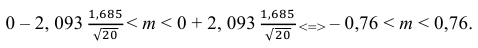
Ответ: (– 0,76; 0,76).

Пример:

По данным десяти независимых измерений найдена оценка квадратического отклонения 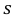 = 0,5. Найти доверительный интервал точности измерительного прибора с надежностью 99 %.
 

Решение. Задача сводится к нахождению доверительного интервала для истинного квадратического отклонения, так как точность прибора характеризуется средним квадратическим отклонением случайных ошибок измерений.

Доверительный интервал для среднего квадратического отклонения находим по формуле:

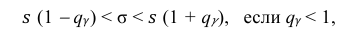
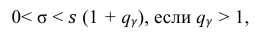
где 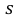  = 0,5 − оценка среднего квадратического отклонения;  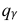– число, определяемое из табл. П 2.4 приложения 2 по заданной доверительной вероятности  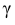 = 0,99 и заданному объему выборки  n = 10.
Находим: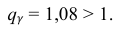  
Тогда можно записать: 

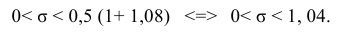
Ответ: (0; 1,04).