
Тепловое равновесие в физике - формулы и определение с примерами
Содержание:
Тепловое равновесие:
Температура — мера средней кинетической энергии теплового движения частиц вещества
В повседневной жизни под температурой мы понимаем степень нагретости тела (холодное, тёплое, горячее). Такой подход является довольно субъективным, он зависит не только от состояния рассматриваемого тела, но и от наших ощущений. Чтобы избежать субъективной неопределённости, необходимо установить способ измерения температуры.
Тепловое равновесие
Если привести в соприкосновение два тела, то молекулы этих тел, взаимодействуя между собой, будут обмениваться энергией. При этом молекулы с большей кинетической энергией передают часть энергии молекулам с меньшей кинетической энергией. В результате средняя кинетическая энергия теплового движения молекул одного тела увеличивается, а другого — уменьшается. Отдающее энергию тело называют более нагретым, а тело, к которому энергия переходит, — менее нагретым. Как показывает опыт, такой переход энергии продолжается до тех пор, пока не установится некоторое состояние, в котором тела могут находиться сколь угодно долго. В этом состоянии степень нагретости тел становится и остаётся одинаковой, следовательно, у тел одинаковая температура. Это учитывают при измерении температуры тела. Термометр приводят в соприкосновение с телом, но отсчёт его показаний выполняют не сразу, а через некоторый промежуток времени. Это необходимо для того, чтобы между термометром и телом установилось тепловое равновесие.
Тепловое равновесие — состояние изолированной физической системы, при котором все её макроскопические параметры остаются неизменными с течением времени.
Под изолированной, или замкнутой, системой понимают систему тел, которая не обменивается энергией с окружающими телами.
Отметим, что у тел, входящих в физическую систему, находящуюся в состоянии теплового равновесия, могут быть различные значения плотности, концентрации, давления и объёма. Однако температура всех тел, входящих в такую систему, всегда одинакова.
Интересно знать:
Понятия «градус» и «температура» появились задолго до изобретения термометра. Знаменитый древнеримский врач Гален (II в.) считал, что все лекарства следует различать по «градусам» (от лат. gradus — ступень) теплоты, холода, сухости и влажности. Гален учил, что одни лекарства оказывают охлаждающее действие, а другие — согревающее. При необходимости следовало смешивать лекарства, чтобы умерить излишнее тепло влажностью, а холод — сухостью. От латинского слова temperature (смешение) возник термин «температура».
Температура и средняя кинетическая энергия поступательного движения молекул газа
Определение температуры должно основываться на такой физической величине, которая характеризует состояние тел и является одинаковой для любых тел, находящихся в состоянии теплового равновесия. Необходимым свойством обладает средняя кинетическая энергия теплового движения частиц вещества. Тепловое движение частиц вещества существенно изменяется при изменении его агрегатного состояния. Максимально простым оно оказывается у одноатомного газа, атомы которого совершают только поступательное движение.
Возьмём несколько сосудов разной вместимости, снабжённых манометрами для измерения давления (рис. 16). Заполнив их различными газами, например аргоном, неоном и гелием, поместим сначала в сосуд с тающим льдом (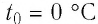
Опытным путём установлено, что в состоянии теплового равновесия, несмотря на различные значения давления 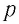 и концентрации
и концентрации 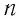 частиц, отношение давления к концентрации
частиц, отношение давления к концентрации 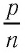 во всех сосудах оказалось практически одинаковым:
во всех сосудах оказалось практически одинаковым: 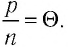 Это отношение для разреженных газов (удовлетворяющих требованиям модели «идеальный газ») зависит только от температуры, и эта зависимость является линейной, т. е.
Это отношение для разреженных газов (удовлетворяющих требованиям модели «идеальный газ») зависит только от температуры, и эта зависимость является линейной, т. е.
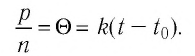
Здесь 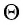 характеризует температуру газов в энергетических единицах (в СИ измеряют в джоулях*);
характеризует температуру газов в энергетических единицах (в СИ измеряют в джоулях*); 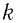 — коэффициент пропорциональности, зависящий от выбора температурной шкалы. В 1899 г. немецкий физик-теоретик Макс Планк (1858—1947) предложил назвать коэффициент
— коэффициент пропорциональности, зависящий от выбора температурной шкалы. В 1899 г. немецкий физик-теоретик Макс Планк (1858—1947) предложил назвать коэффициент 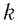 постоянной Больцмана в честь австрийского физика Людвига Больцмана (1844 — 1906), одного из основателей молекулярно-кинетической теории газов:
постоянной Больцмана в честь австрийского физика Людвига Больцмана (1844 — 1906), одного из основателей молекулярно-кинетической теории газов:
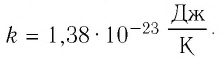
Если для измерения температуры использовать абсолютную температурную шкалу, то при определении числового значения температуры по этой шкале полагают:

Абсолютную (термодинамическую) шкалу температур предложил в 1848 г. выдающийся английский физик Уильям Томсон (1824—1907), удостоенный за работы в области физики в 1892 г. титула лорда Кельвина. Поэтому эту шкалу обычно называют шкалой Кельвина.
Шкала Кельвина совершенно не зависит от физических свойств каких бы то ни было веществ, поэтому её можно считать абсолютной и универсальной.
Нулевая точка по шкале Кельвина соответствует самой низкой теоретически возможной температуре (абсолютный нуль температуры). Температура тающего льда по этой шкале 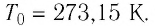 Связь между температурами по шкале Цельсия
Связь между температурами по шкале Цельсия 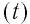 и по шкале Кельвина (Т) имеет вид:
и по шкале Кельвина (Т) имеет вид: 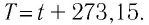
* Единица измерения температуры джоуль неудобна. Например, температура кипения воды, выраженная в джоулях: 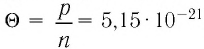 Дж.
Дж.
Единица температуры по абсолютной шкале один кельвин (1 К) является основной единицей температуры в СИ и совпадает с одним градусом (1 °С) по шкале Цельсия. Поэтому разность температур по шкале Кельвина и по шкале Цельсия одинакова, т. е. 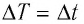 (рис. 17).
(рис. 17).

От теории к практике:
Выразите по шкале Кельвина температуру тела здорового человека.
Из основного уравнения молекулярно-кинетической теории идеального газа (3.2) следует: 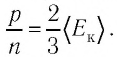 Таким образом, учитывая выражение (4.1), можно записать:
Таким образом, учитывая выражение (4.1), можно записать: 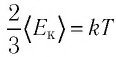 или
или

Соотношение (4.2) устанавливает связь между абсолютной температурой Т идеального газа и средней кинетической энергией 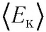 поступательного движения его частиц. Таким образом, из формулы (4.2) следует, что средняя кинетическая энергия поступательного движения частиц идеального газа пропорциональна его абсолютной температуре.
поступательного движения его частиц. Таким образом, из формулы (4.2) следует, что средняя кинетическая энергия поступательного движения частиц идеального газа пропорциональна его абсолютной температуре.
Средняя кинетическая энергия поступательного движения молекул газов, находящихся в состоянии теплового равновесия, одинакова для разных газов и не зависит от массы молекулы газа.
Этот вывод, основанный на экспериментах с разреженными газами, справедлив для жидкостей и твёрдых тел.
Уравнение (4.2) можно записать следующим образом: 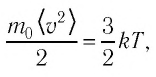 откуда
откуда
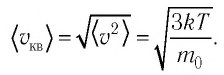
С учётом формулы (4.1) основное уравнение молекулярно-кинетической теории идеального газа может быть записано в виде:

Из уравнения (4.3) следует, что при одинаковых значениях абсолютной температуры Т и концентрации 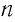 частиц давление любых газов одинаково, независимо от того, из каких частиц они состоят.
частиц давление любых газов одинаково, независимо от того, из каких частиц они состоят.
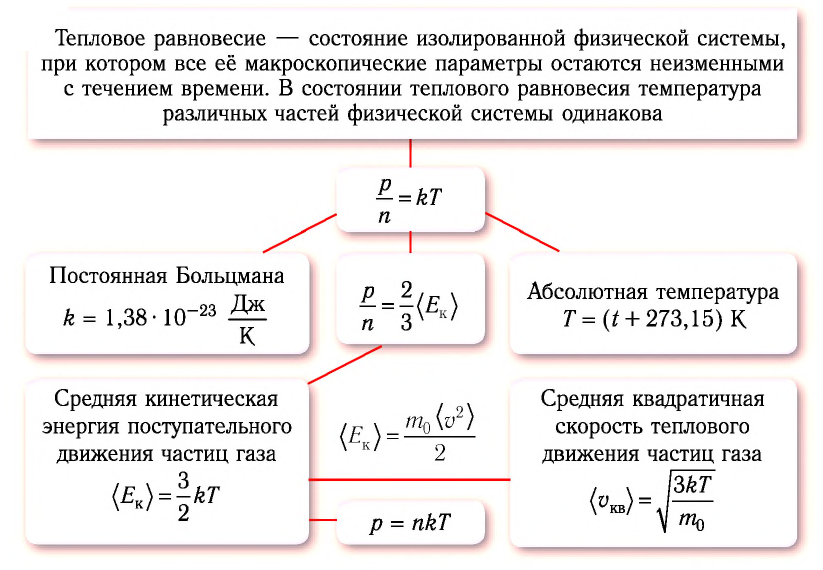
Пример №1
Сравните средние квадратичные скорости атомов гелия и молекул кислорода, если газы находятся в состоянии теплового равновесия.
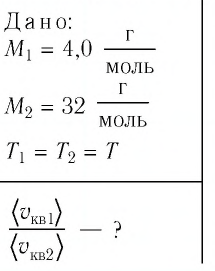
Решение. Средняя квадратичная скорость теплового движения частиц газа 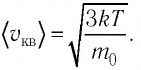 Поскольку масса одной молекулы вещества
Поскольку масса одной молекулы вещества 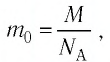 то
то
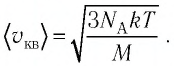 Так как газы находятся в состоянии теплового равновесия, т. е.
Так как газы находятся в состоянии теплового равновесия, т. е. 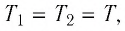 то средние квадратичные скорости атомов гелия
то средние квадратичные скорости атомов гелия
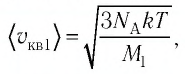
молекул кислорода 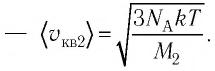
Тогда: 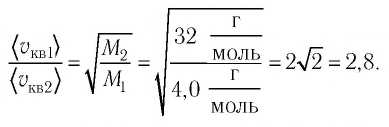
Ответ: в состоянии теплового равновесия средняя квадратичная скорость атомов гелия в 2,8 раза больше средней квадратичной скорости молекул кислорода.
Пример №2
В баллоне вместимостью 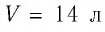 находился газ, абсолютная температура которого
находился газ, абсолютная температура которого 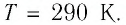 Расходуя газ, из баллона выпустили
Расходуя газ, из баллона выпустили 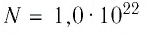 молекул. Определите, на сколько уменьшилось давление газа в баллоне, если через некоторый промежуток времени его температура увеличилась до первоначального значения.
молекул. Определите, на сколько уменьшилось давление газа в баллоне, если через некоторый промежуток времени его температура увеличилась до первоначального значения.
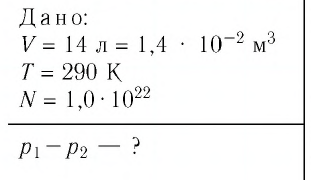
Решение. Начальное давление газа
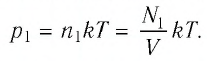
После того как израсходовали часть газа, а его температура увеличилась до первоначального значения Т, давление газа стало
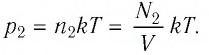
Тогда убыль давления газа:
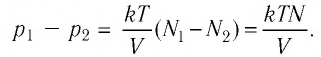
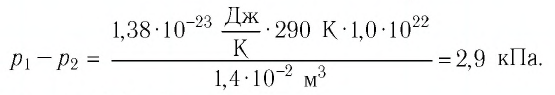
Ответ: 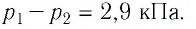
Тепловое равновесие, температура
Понятие температуры занимает важное место в повседневной жизни. Так, говоря температура, мы обычно подразумеваем степень нагретости (горячее, теплое, холодное) тела. Такое рассмотрение в достаточной степени субъективно, потому что температура зависит не только от состояния рассматриваемого тела, но и от нашей чувствительности.
Тепловое равновесие:
Известно, что при соприкосновении двух тел с разными температурами между ними происходит теплообмен: тепло переходит от тела с высокой температурой к телу с более низкой температурой. Этот процесс продолжается до тех пор, пока температуры обоих тел не сравняются. Этот факт учитывается при измерении температуры тел — термометр приводится в соприкосновение с телом, но его показания снимаются не сразу, а через определенный промежуток времени, в течение которого между телом и термометром устанавливается тепловое, или так называемое термодинамическое равновесие. При термодинамическом равновесии макроскопические параметры системы остаются постоянными, то есть изменение агрегатного состояния вещества не происходит.
Тепловое или термодинамическое равновесие - это состояние системы, когда ее макроскопические параметры длительное время остаются неизменными.
Состояние теплового равновесия системы характеризуется температурой.
Температура - физическая величина, характеризующая состояние теплового равновесия макроскопической системы: в состоянии теплового равновесия температура всех частей системы одинакова.
Качественное и количественное определение температуры должно основываться на определении физической величины, которая, во-первых, должна характеризовать состояние тела, во-вторых, должна быть одинакова для всех тел, находящихся в тепловом равновесии. Такой величиной является средняя кинетическая энергия поступательного движения молекул вещества. Можно легко определить ее значения для поступательно движущихся молекул одноатомного идеального газа.
С этой целью был поставлен следующий интересный эксперимент: три баллона разного объема, снабженные манометрами (прибор для измерения давления), заполнены различными газами, например, аргоном, неоном и гелием. Баллоны помещаются сначала в тающий лед  а затем в кипящую воду
а затем в кипящую воду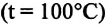 (b).
(b).
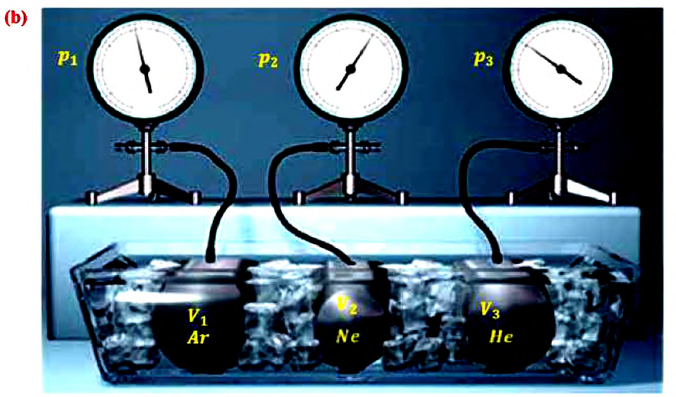
Произведенные вычисления показывают, что в обоих случаях (и при температуре 0°С, и при температуре 100°С) при достижении теплового равновесия, отношение 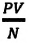 во всех баллонах остается постоянным, несмотря на то, что давление и концентрация газов разная:
во всех баллонах остается постоянным, несмотря на то, что давление и концентрация газов разная:
при 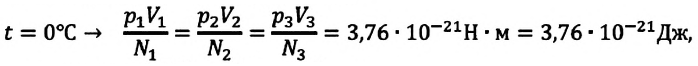
при 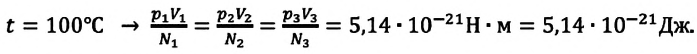
Если принять во внимание, что 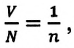 то получается, что при тепловом равновесии отношение давления газа к его концентрации равно постоянной величине, измеряемой в единицах энергии — джоулях:
то получается, что при тепловом равновесии отношение давления газа к его концентрации равно постоянной величине, измеряемой в единицах энергии — джоулях:

Здесь 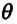 (тета) — является постоянной величиной, зависящей для всех разреженных газов, приближенных к идеальному газу, только от температуры:
(тета) — является постоянной величиной, зависящей для всех разреженных газов, приближенных к идеальному газу, только от температуры:

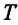 - абсолютная температура,
- абсолютная температура, 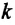 - является коэффициентом пропорциональности и называется постоянной Больцмана, в честь австрийского физика Людвига Больцмана (1844—1906). Опытным путем было определено, что постоянная Больцмана равна:
- является коэффициентом пропорциональности и называется постоянной Больцмана, в честь австрийского физика Людвига Больцмана (1844—1906). Опытным путем было определено, что постоянная Больцмана равна:
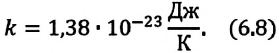
Постоянная Больцмана связывает температуру 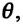 измеряемую в единицах энергии, с абсолютной температурой
измеряемую в единицах энергии, с абсолютной температурой 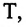 измеряемой в Кельвинах. Из выражений (6.6) и (6.7) получается выражение для давления идеального газа:
измеряемой в Кельвинах. Из выражений (6.6) и (6.7) получается выражение для давления идеального газа:

Выражение (6.9) может быть использовано для определения абсолютной температуры в Кельвинах:

Формула (6.10) дает возможность создания новой температурной шкалы. Такая температурная шкала, называемая шкалой абсолютных температур, была предложена в 1848 году английским физиком Уильямом Томсоном (1824-1907). За вклад в области физики в 1892 году он был награжден титулом лорда Кельвина.
Поэтому предложенная им шкала температур называется шкалой Кельвина. Нулевая точка шкалы Кельвина, то есть температура абсолютного нуля, это самая низкая температура, какая возможна теоретически и практически. Согласно этой шкале температура плавления льда равна 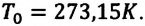 Соотношение между температурной шкалой Цельсия и шкалой Кельвина следующая:
Соотношение между температурной шкалой Цельсия и шкалой Кельвина следующая: 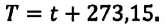 При вычислениях это соотношение можно записать в более простой форме:
При вычислениях это соотношение можно записать в более простой форме:

Единица измерения абсолютной температуры, являющейся основной в СИ - Кельвин 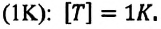 Эта температура соответствует температуре
Эта температура соответствует температуре 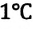 по шкале Цельсия. Поэтому, разность температур и по шкале Кельвина, и по шкале Цельсия одинакова:
по шкале Цельсия. Поэтому, разность температур и по шкале Кельвина, и по шкале Цельсия одинакова:
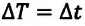 (с).
(с).

Температура - мера средней кинетической энергии молекул. На самом деле из сравнения выражений (6.4) и (6.9) получаем, что абсолютная температура, являющаяся макроскопическим параметром идеального газа (или разреженного газа), связана со средней кинетической энергией молекул, являющейся ее микроскопическим параметром:
• Средняя кинетическая энергия поступательного движения молекул газа прямо пропорциональна его абсолютной температуре:

Из формулы (6.12) ясно виден физический смысл температуры:
Температура - это мера средней кинетической энергии поступательного движения молекул тела. Это утверждение так же верно для жидкостей и твердых тел. Из формулы видно, что среднее значение кинетической энергии поступательного движения, а значит, и средняя квадратичная скорость молекул при абсолютном нуле равна нулю.
Средняя квадратичная скорость молекул
Из формул (6.1), (6.3) и (6.5) можно вычислить среднюю квадратичную скорость молекул:
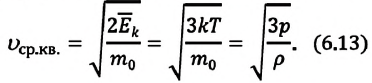
| Рекомендую подробно изучить предметы: |
| Ещё лекции с примерами решения и объяснением: |