Теория статистической проверки гипотез - определение и вычисление с примерами решения

Содержание:

Теория статистической проверки гипотез

Пусть имеется выборка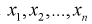

Тогда нулевой гипотезой 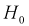 называют основную (проверяемую) гипотезу, которая утверждает, что различие между сравниваемыми величинами отсутствует.
 

Альтернативной (конкурирующей, противоположной) гипотезой Н называется гипотеза, которая принимается тогда, когда отвергается нулевая.

Целью статистической проверки гипотез является выбор критерия по выборке 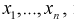 на основании которого принимается гипотеза  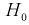или отклоняется в пользу альтернативной. При этом возможны ошибки двух видов:

1. Отклонение 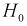, когда она на самом деле верна - ошибка первого рода. Вероятность этой ошибки обозначается а и называется уровнем значимости.
2. Принятие 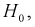 когда она на самом деле не верна - ошибка второго рода, вероятность ошибки - .

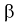Чем серьезнее будут последствия ошибки первого рода, тем меньше надо выбирать уровень значимости 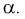 Обычно выбирают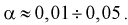
 

Статистической характеристикой Z гипотезы 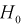 называется некоторая случайная величина, определяемая по выборке, для которой известен закон распределения.
 

Областью отклонения (критической областью) 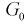 называется область, при попадании в которую статистической характеристики Z гипотеза  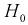отклоняется.
 

Дополнение области отклонения до всех возможных значений статистической характеристики Z называется областью принятия G.

При попадании статистической характеристики Z в область принятия ги­потеза 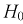 принимается. На рис. 11.1 изображены область отклонения  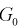и область принятия G . Разделяет их точка на числовой оси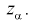

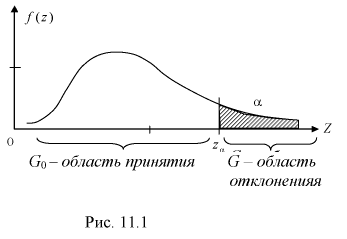
При попадании Z в область принятия гипотеза 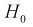 принимается. По существу область принятия есть доверительный интервал для статистической характеристики Z с доверительной вероятностью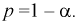

Область отклонения 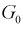 выбирается таким образом, чтобы вероятность попадания в нее статистической характеристики Z при условии, что  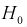верна, равнялась уровню значимости  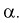То есть область отклонения удовлетворяет условию:

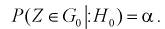             (11.1)

С другой стороны, для того чтобы уменьшить вероятность ошибки второго рода при выбранном  область отклонения , удовлетворяющую условию 1, нужно выбрать таким образом, чтобы вероятность попадания в нее статистической характеристики Z при условии, что верна альтернативная гипотеза 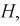 была максимальной, т. е.

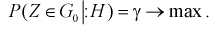
Вероятность  - называется мощностью критерия проверки гипотез.
Так как события , - противоположны, то можно написать

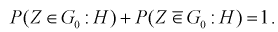
Таким образом, имеем

где 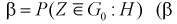 - вероятность совершения ошибки второго рода).

Отметим, что ошибка первого рода существенней, поэтому а мы выбираем, а р - нет (принимаем полученное значение).

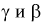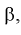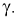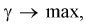Из (11.2) следует, что между  существует простая зависимость и чтобы уменьшить  надо увеличить мощность критерия  Если  то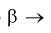

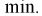
Между 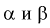 простой функциональной связи не существует, можно только сказать, что с увеличением одной, другая уменьшается и наоборот.

На рис. 11.2 приведены две кривые плотности распределения: одна кривая 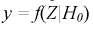 - когда верна гипотеза  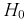, другая кривая 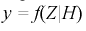- когда верна альтернативная гипотеза Н.

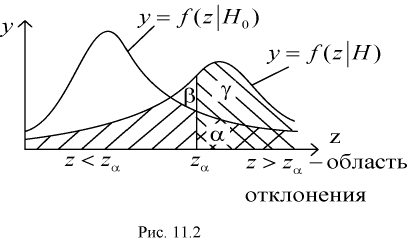
Из рис. 11.2 видно, что при уменьшении 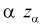, возрастает, область отклонения сужается и, следовательно, уменьшается вероятность отклонения гипотезы  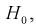если она верна. Вместе с тем при сужении области отклонения  расширяется область принятия G и увеличивается вероятность принятия гипотезы 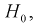 если она на самом деле не верна. Поэтому нельзя брать 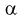слишком малой.
Гипотезы бывают двух видов - параметрические и непараметрические.

Параметрические гипотезы - это гипотезы о проверке параметров законов распределения.

Непараметрические - это гипотезы о виде закона распределения.

Проверка гипотезы равенства математических ожиданий при неизвестной дисперсии (критерий Стьюдента)

Пусть Хи У - независимые нормальные случайные величины.
Введем обозначения:

Пусть дисперсии этих случайных величин равны и неизвестны:

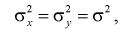
где 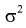 - не предполагается известным.
Пусть даны выборки

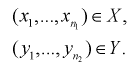
По выборкам найдем критерий проверки гипотезы 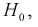, состоящей в том, что математические ожидания этих случайных величин одинаковы:

При альтернативной гипотезе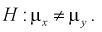

Известно, что случайные величины

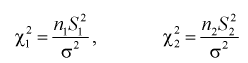
имеют распределение 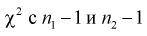 степенями свободы, где

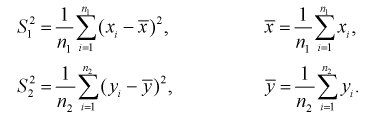
Сумма независимых случайных величин с распределением 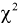 имеет то же распределение  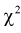с суммарным числом степеней свободы:

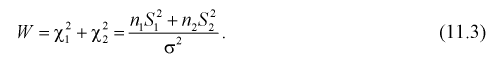
Случайная величина W имеет распределение 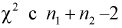 степенями свободы, (этот факт не очевиден, но несложно показать с помощью характеристических функций).

Ранее мы показывали, что несмещенной оценкой математического ожидания является выборочное среднее. Поэтому для проверки гипотезы 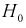 возьмем разность между оценками математических ожиданий:  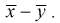Нормируем эту разность, т. е. сделаем безразмерной. Для этого разделим ее на  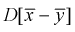и обозначим как U:

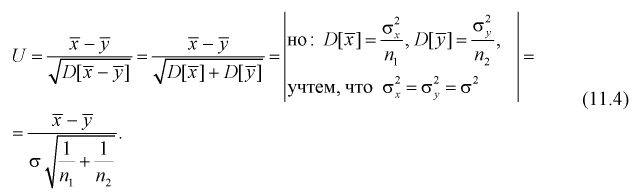
Очевидно, что случайная величина U имеет нормальное распределение, т. к. X и Y нормально распределены. Если проверяемая гипотеза 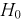 о равенстве математических ожиданий выполняется  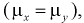то имеем:

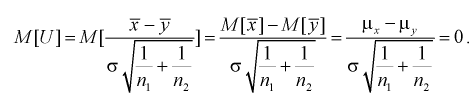
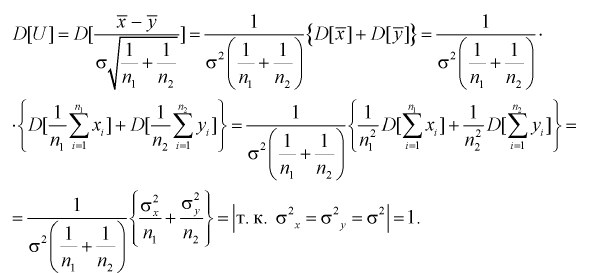
Таким образом, если гипотеза  верна, то случайная величина U имеет нормированный нормальный закон распределения.

Рассмотрим случайную величину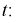

где 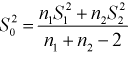 где ; - ооъединенная выборочная дисперсия.
Случайную величину t можно представить в следующем виде через ранее введенные Un W:

Действительно:

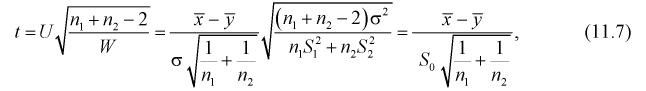
т. е. правые части (11.5) и (11.6 или 11.7) совпадают.

Но величина t (11.6) имеет распределение Стьюдента с 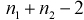 степенями свободы. Это следует из того, что U имеет нормированное нормальное распределение при условии, что  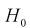- верна. W - имеет распределение  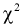с 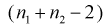 степенями свободы, кроме того величины U и W независимы. Таким образом, величина t определяется по (11.5) и имеет распределение Стью­дента с  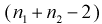степенями свободы, если верна проверяемая гипотеза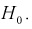

Эту величину t (11.5) примем за статистическую характеристику Z. Про­верка гипотезы о равенстве .математических ожиданий состоит в следующем.

По таблицам распределения Стьюдента для заданного уровня значимости 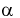 или доверительной вероятности  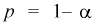и числу степеней свободы  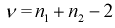находим квантиль  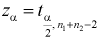, удовлетворяющий условию (на рис. 11.3 изображена кривая распределения Стьюдента и заштрихована область отклонения  ):

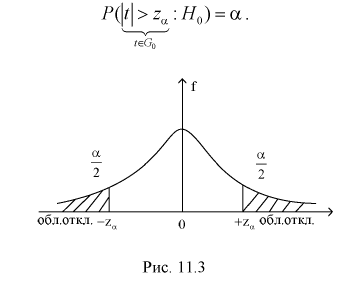
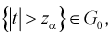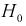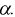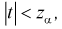Тогда если фактически найденное по выборкам значение статистиче­ской характеристики t (11.5) удовлетворяет условию  то проверяемую гипотезу  о равенстве математических ожиданий отклоняем как несогласующуюся с результатами выборочных данных; при этом вероятность ошибки равна  Если  то гипотеза 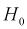принимается, математические ожидания случайных величин Х и Y одинаковы.

Проверка гипотезы о равенстве дисперсий (критерий Фишера)

Пусть Х и Y - нормальные независимые случайные величины. Обозначим их дисперсии:

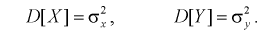
По выборкам 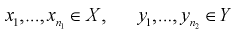 найдем критерий проверки гипотезы  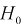состоящей в том, что дисперсии этих случайных величин равны

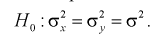
При альтернативной гипотезе .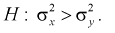
Такая гипотеза выбирается, например, при 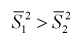, где 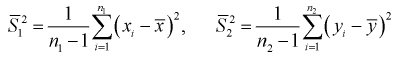- модифицированные выборочные дисперсии.

В качестве статистической характеристики возьмем случайную величину

Если гипотеза 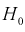, о равенстве дисперсии верна, то случайная величина F имеет распределение Фишера с  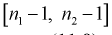степенями свободы. Покажем это, представляя числитель и знаменатель (11.8) в следующем виде:

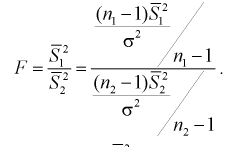
Видим, что величина 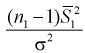 имеет распределение  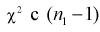степенью свободы,  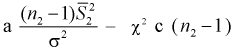степенями свободы. Следовательно, согласно определению (см. раздел 9.5, формула (9.7)), случайная величина F имеет распределение Фишера с  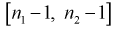степенями свободы.
 

Проверка гипотезы 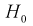состоит в следующем:

Из таблиц распределения Фишера по выбранному уровню значимости 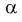 и числу степеней свободы  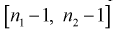находим квантиль  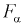, который удовлетворяет условию  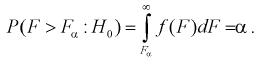Ha рис. 11.4 изображена кривая распределения Фишера с числом степеней свободы  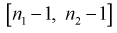и заштрихована область отклонения  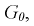площадь которой области равна  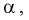отмечен квантиль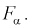

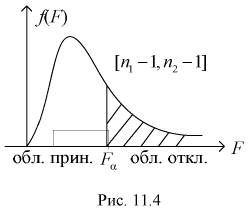
По выборкам, используя (11.8), определяем значение статистической характеристики F. Если фактически вычисленное по формуле (11.8) значение F окажется больше табличного 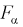 (как видно из рис. 11.4, мы попадаем в область отклонения), то гипотезу о равенстве дисперсий отклоняем как не согласующуюся с выборкой. При этом вероятность ошибки равна  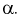В противном случае, когда 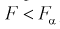, принимается гипотеза  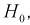т. е. дисперсии случайных величин Х и Yравны.
 

Пример:

Пусть X - чувствительность телевизоров марки «Горизонт», Y - чувствительность телевизоров марки «Витязь». Проведены выборочные измерения чувствительности телевизоров для 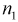 = 7 телевизоров марки «Горизонт» и  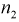= 6 телевизоров марки «Витязь». Результаты измерений чувствительности в  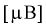представлены в таблицах.

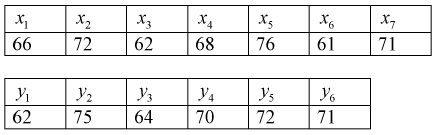
Определить лучшую марку телевизора, если лучшим будет тот, у которого чувствительность в 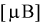 будет меньше.

Найдем по результатам измерений средние значения чувствительности, вычисляя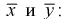

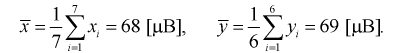
Можно ли сказать, что чувствительность телевизоров марки «Горизонт» лучше? Нет, т. к. выборки, выборочные средние 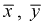 и разность между ними - элементы случайные.

Сначала убедимся в равенстве дисперсий по критерию Фишера - гипотеза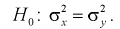 

Вычислим несмещенные оценки дисперсий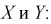

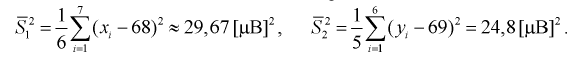
Используя (11.8), найдем значение статистической характеристики F:

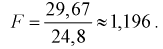
По таблицам распределения Фишера для [6;5] степеней свободы, задавая уровень значимости 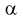 = 0,05, найдем квантиль - 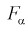= 4,95. Сравнивая  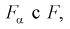видим, что 1,196 < 4,95. Значит, гипотеза  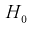принимается, т. е. дисперсии случайных величин X и Y равны.

Теперь проверим гипотезу о равенстве математических ожиданий случайных величин X и Y , применяя критерий Стьюдента.
Гипотеза 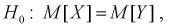 т. е. чувствительность телевизоров марки «Горизонт» и «Витязь» одинакова.

Найдем объединенную выборочную дисперсию:

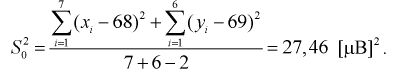
По формуле (11.5) вычислим статистическую характеристику t :

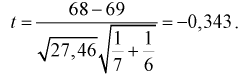
Задавая уровень значимости 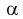 = 0,05 для числа степеней свободы v = 7 + 6 - 2 = ll, по таблицам распределения Стьюдента находим квантиль  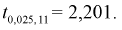Сравнивая  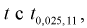видим, что |0,343| <2,201, значит, гипотезу о равенстве чувствительности телевизоров марки «Горизонт» и «Витязь» принимаем.

Проверка гипотезы о законе распределения генеральной случайной величины. Критерий Пирсона

Проверка гипотезы о законе распределения генеральной случайной величины. Критерий Пирсона. (Критерий согласия )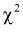

Пусть задана генеральная случайная величинами выборка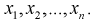
Если по выборке построить гистограмму, то по виду гистограммы можно выдвинуть гипотезу о виде закона распределения генеральной случайной величины X. Тогда в качестве нулевой гипотезы 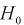 будет предположение, что случайная величина X имеет плотность распределения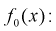

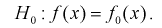
При альтернативной гипотезе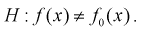

Обычно для построения гистограммы равноинтервальным способом разбивают весь диапазон выборочных значений случайной величины X на 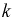 одинаковых интервалов. Если 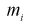- число выборочных значений, попавших в  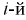интервал, то  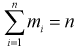- объем выборки. Введем случайную величину  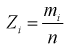относительную частоту попадания случайной величины X в  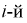интервал. Тео­ретическая вероятность  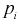попадания значений случайной величины X в  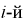интервал может быть определена как  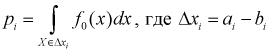- длина  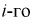интервала,  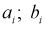- границы  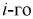интервала.

Рассмотрим событие, состоящее в том, что случайная величина X попадет в интервал 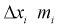 раз. Тогда введем случайную величину Y, равную числу попаданий случайной величины в  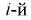интервал  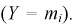Вероятности возможных ее значений определяются по формуле Бернулли, случайная величина У имеет биномиальный закон распределения, и ее числовые характеристики имеют вид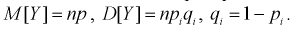

Для введенной ранее случайной величины 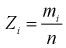 определим числовые характеристики:

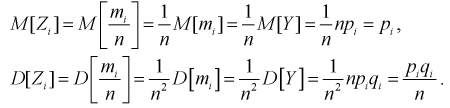
Проведем нормировку случайной величины 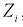 для этого мы ее центрируем, сделаем безразмерной, разделив на  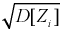и обозначим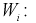

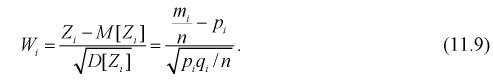
Эта величина распределена по биномиальному закону, т. к. в нее входит случайная величина  Образуем сумму квадратов случайных величин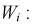

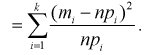
Сумма квадратов нормированных нормальных случайных величин (как было показано ранее) имеет распределение 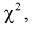 обозначим

Эта случайная величина имеет закон распределения 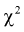 с числом степеней свободы
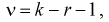                              (11.11)
где 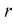 - число параметров закона распределения, оцениваемых по выборочным данным.

Анализируя правые части формул (11.9) и (11.10), можно отметить, что в критерии согласия 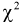 фактически сравниваются эмпирические и теоретические частоты распределения.
 

Проверка гипотезы состоит в следующем. Задаем уровень значимости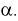

По таблицам 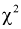 - распределения для заданных  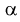и числу степеней свободы  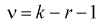находим квантиль  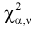, удовлетворяющий условию  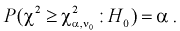По формуле (11.10) вычисляем значение  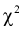. Сравнивая рассчитанное значение  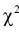с квантилем 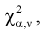, найденным по таблицам, принимаем одно из двух решений:

1. Если 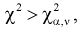 то нулевая гипотеза  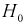отвергается в пользу альтернативной Н, т. е.  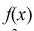не согласуется с результатами эксперимента.
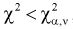2. Если , то 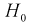, принимается, т. е.  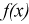согласуется с эксперимен­тальными данными, закон распределения  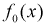подтверждается. При этом вероятность ошибки равна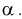

Критерий Романовского

Рассмотрим неравенство
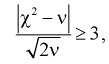                               (11.12)
где 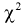 вычисляется по формуле (11.10);

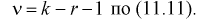
Проверка гипотезы состоит в следующем: если это неравенство выполняется 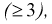 то расхождение теоретических и экспериментальных данных неслучайно, т. е. закон распределения не подтверждается, гипотеза  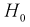отклоняется.
В противном случае гипотеза 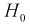 подтверждается, действительно случайная величина X имеет плотность распределения 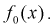Этот критерий хорош тем, что для проверки гипотезы не требуются таблицы 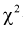- распределения.

Критерий согласия Колмогорова

В критерии согласия А. Н. Колмогорова проводится сравнение эмпириче­ской и теоретической функций распределения. Укажем этапы проверки гипотез этим критерием.

1. По выборке 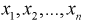 строится вариационный ряд и график эмпирической функции распределения.

2. По виду графика функции распределения выдвигается гипотеза о виде закона распределения генеральной случайной величины X. Тогда в качестве нулевой гипотезы 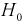 будет предположение, что генеральная случайная величина X имеет функцию распределения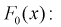

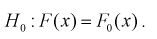
При альтернативной гипотезе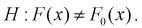

3. По выборке 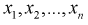 находят точечные оценки параметров теоретической функции распределения 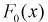, используя метод моментов или метод наибольшего правдоподобия.

4. На графике эмпирической функции распределения строится график теоретической функции распределения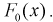

5. Путем сравнения графиков вычисляется максимальное значение моду­ля отклонения значений эмпирической функции распределения от теоретиче­ской функции распределения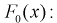

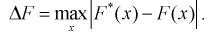
6. Рассчитывают значение 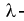критерия Колмогорова:

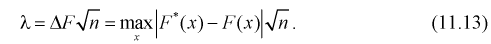
7. Задавая уровень значимости а , определяем квантиль из условия 

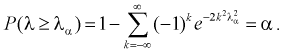
Отметим, что самостоятельно решать это уравнение не надо, поскольку составлены таблицы квантилей распределения Колмогорова, из которых по заданному уровню значимости 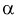 определяем квантиль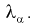
 

Сравнивая значение 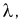 рассчитанное по формуле (11.13) с квантилем  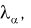делаем следующие выводы:

• а) если 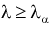, то гипотеза  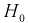отклоняется;
• б) если 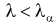 , то гипотеза принимается, закон распределения под­тверждается, т. е. действительно генеральная случайная величина X имеет функцию распределения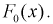

Следует отметить, что критерий Колмогорова применяется тогда, когда полностью известен закон распределения функции распределения F(x) и зна­чения ее параметров. При решении практических задач это не всегда удается выполнить. Для этого прибегают к некоторым дополнительным исследованиям: применяют вероятностные бумаги, строят гистограммы и т. д. Это помогает правильно подобрать теоретический закон распределения для функции распределения F(x). Но в этом случае неизвестны ее параметры. И если их оценивать по этой же выборке, то это может привести к ошибочным выводам в отношении принятой гипотезы. В этом случае следует использовать другие критерии согласия, например  .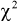
 

Пример:

Проведено 100 измерений расстояния радиодальномером до цели. Результаты представлены в виде статистического ряда 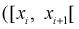 - границы интервалов в [км],  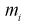- число выборочных значений, попавших в 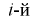интервал).
Оценить закон распределения ошибки измерения дальности радиодальномером.

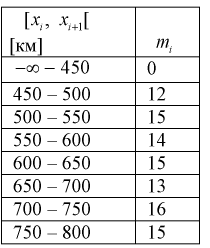
Занесем в таблицу значения относительных частот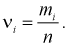

Анализ значений относительных частот позволяет выдвинуть гипотезу о равномерном законе распределения. Теоретическая функция распределения для этого закона имеет вид

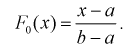
Принимаем а = 450, b = 800. Полагая 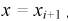 для каждого интервала, рассчитываем  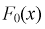в этих точках и заносим результат в таблицу. Зная  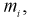рассчитаем эмпирическую функцию распределения  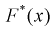в точках  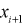для каждого интервала:  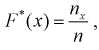где 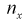 - число значений  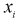меньших заданного х,  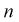- объем выборки. Рассчитаем разность:  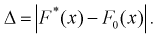Данные заносим в таблицу.

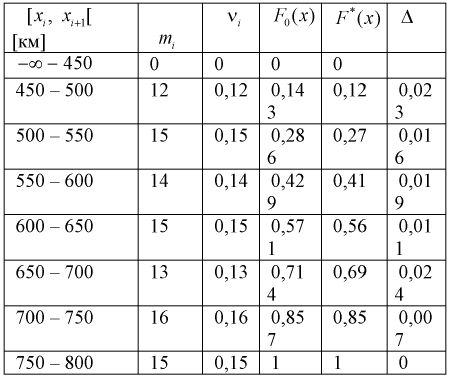
Вычисляем критерий Колмогорова по формуле (11.13), учитывая, что из таблицы 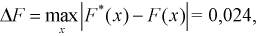тогда 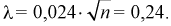 Задавая уровень значимости  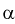- 0,05, по таблице квантилей Колмогорова находим кван­тиль  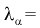1,358. Поскольку  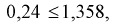то гипотеза  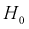принимается, т. е. действительно генеральная случайная величина X имеет функцию распределения  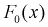c равномерным законом распределения.