
Теория пар сил в теоретической механике
Содержание:
Теория пар:
Пару сил в механике рассматривают как одно из основных понятий наряду, с понятием силы.
Что такое пара сил
Парой сил называют систему двух равных по модулю параллельных сил, направленных в противоположные стороны (рис. 24).
Пара сил не составляет системы сил, эквивалентной нулю.
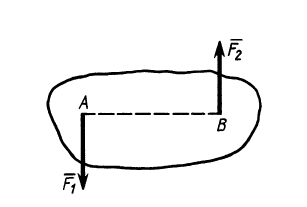
Рис. 24
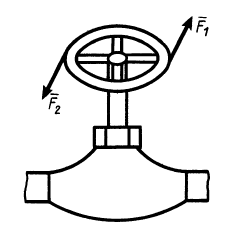
Рис. 25
Известно, что под действием пары сил свободное твердое тело выходит из равновесия. Обычно пару сил 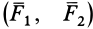 прилагают к телу, которое должно вращаться, например к маховику вентиля при его закрывании и открывании (рис. 25). Поэтому пару сил нельзя заменить одной силой и, следовательно, она не имеет равнодействующей, а является такой системой сил, упростить которую нельзя. Каждая из сил, входящих в состав пары сил, имеет свойства обычных сил.
прилагают к телу, которое должно вращаться, например к маховику вентиля при его закрывании и открывании (рис. 25). Поэтому пару сил нельзя заменить одной силой и, следовательно, она не имеет равнодействующей, а является такой системой сил, упростить которую нельзя. Каждая из сил, входящих в состав пары сил, имеет свойства обычных сил.
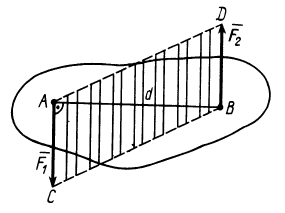
Рис. 26
Пара сил, действующая на твердое тело, характеризуется прежде всего плоскостью действия, аналогично тому, как сила характеризуется линией действия. Плоскостью действия пары сил называют плоскость, в которой расположены силы пары.
Для количественной характеристики действия пары сил на твердое тело и указания направления, в котором пара сил стремится вращать тело в плоскости действия, введем понятие алгебраического момента пары сил.
Алгебраическим моментом пары сил называют взятое со знаком плюс или минус произведение одной из сил пары на плечо пары сил.
Плечом пары сил 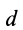 называют кратчайшее расстояние между линиями действия сил пары (рис. 26).
называют кратчайшее расстояние между линиями действия сил пары (рис. 26).
Алгебраический момент пары обозначим 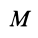 или
или 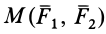 . Согласно определению,
. Согласно определению,
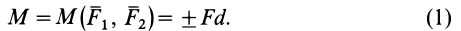
Алгебраический момент пары сил выражается в тех же единицах, что и алгебраический момент силы относительно точки.
Алгебраический момент пары сил имеет знак плюс, если пара сил стремится вращать тело против часовой стрелки, и знак минус, если пара сил стремится вращать тело по часовой стрелке.
Алгебраический момент пары сил не зависит от переноса сил пары вдоль своих линий действия и может быть равен нулю, если линии действия сил пары совпадают, т. е. в случае двух равных по модулю, но противоположных по направлению сил, действующих вдоль одной прямой. Такая система двух сил, как известно, эквивалентна нулю. Алгебраический момент пары сил численно равен площади параллелограмма, построенной на силах пары:

Теорема об эквивалентности двух пар сил, расположенных в одной плоскости
Докажем, что пары сил, расположенные в одной плоскости, по своему действию на тело отличаются одна от другой только алгебраическими моментами.
Две пары сил называют эквивалентными, если их действие на твердое тело одинаково при прочих равных условиях.
Докажем теперь следующую теорему об эквивалентности двух пар сил: пару сил, действующую на твердое тело, можно заменить другой парой сил, расположенной в той же плоскости действия и имеющей одинаковый с первой парой алгебраический момент. Иначе: две пары сил, расположенные в одной плоскости, эквивалентны, если они имеют одинаковые алгебраические моменты.
Пусть на твердое тело действует пара сил 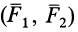 с алгебраическим моментом
с алгебраическим моментом 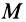 (рис. 27). Перенесем силу
(рис. 27). Перенесем силу 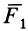 в точку
в точку 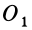 , а силу
, а силу 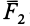 — в точку
— в точку 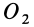 , проведем через точки
, проведем через точки 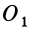 и
и 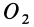 две любые параллельные прямые, пересекающие линии действия сил пары и лежащие, следовательно, в плоскости действия заданной пары сил. Соединив прямой точки
две любые параллельные прямые, пересекающие линии действия сил пары и лежащие, следовательно, в плоскости действия заданной пары сил. Соединив прямой точки 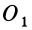 и
и 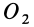 , разложим силы
, разложим силы 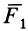 в точке
в точке 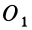 и
и 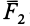 в точке
в точке 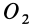 по правилу параллелограмма, как указано на рис. 27. Тогда
по правилу параллелограмма, как указано на рис. 27. Тогда
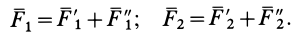
Так как силы 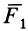 и
и 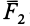 образуют пару сил, то
образуют пару сил, то
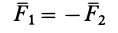
и, следовательно,
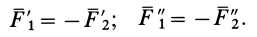
Итак,
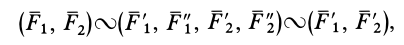
так как
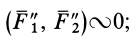
следовательно, эту систему двух сил можно отбросить.
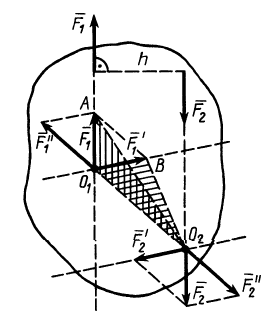
Рис. 27
Таким образом, заданную пару сил 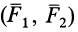 заменим другой парой сил
заменим другой парой сил 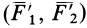 . Докажем, что алгебраические моменты у этих пар сил одинаковы. Направление вращения у них одно и то же. Имеем
. Докажем, что алгебраические моменты у этих пар сил одинаковы. Направление вращения у них одно и то же. Имеем
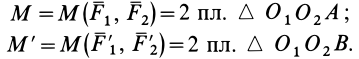
Но 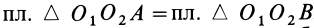 так как эти треугольники имеют общее основание
так как эти треугольники имеют общее основание 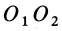 и равные высоты (их вершины расположены на общей прямой, параллельной основанию).
и равные высоты (их вершины расположены на общей прямой, параллельной основанию).
Таким образом, теорема доказана и можно сделать следующие выводы:
- а) пару сил как жесткую фигуру можно как угодно поворачивать и переносить в ее плоскости действия;
- б) у пары сил можно изменять плечо и силы, сохраняя при этом алгебраический момент пары и плоскость действия.
Эти операции над парами сил не изменяют их действия на твердое тело.
Теорема о переносе пары сил в параллельную плоскость
Действие пары сил на твердое тело не изменяется от переноса этой пары сил в параллельную плоскость (рис. 28).
Для доказательства этой теоремы к паре сил 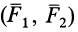 в точках
в точках 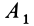 и
и 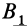 , где перпендикуляры, опущенные из точек
, где перпендикуляры, опущенные из точек 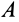 и
и 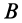 плоскости
плоскости 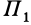 , пересекаются параллельной ей плоскостью
, пересекаются параллельной ей плоскостью 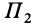 , приложим две системы сил
, приложим две системы сил 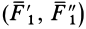 и
и 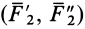 , каждая из которых эквивалентна нулю, т. е.
, каждая из которых эквивалентна нулю, т. е.
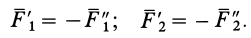
Выберем силы 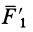 и
и 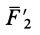 так, чтобы они удовлетворяли условиям
так, чтобы они удовлетворяли условиям
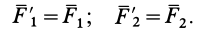
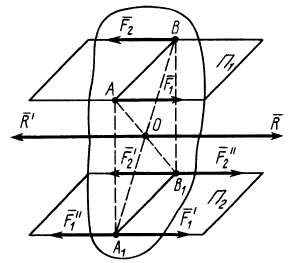
Рис. 28
Сложим две равные и параллельные силы 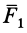 и
и 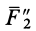 . Их равнодействующая
. Их равнодействующая 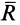 параллельна этим силам, равна их сумме и приложена посередине отрезка
параллельна этим силам, равна их сумме и приложена посередине отрезка 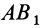 в точке
в точке 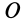 , так как складываются равные параллельные силы. Равнодействующая
, так как складываются равные параллельные силы. Равнодействующая 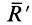 двух равных параллельных сил
двух равных параллельных сил 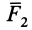 и
и 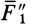 тоже равна их сумме, параллельна им и приложена на середине отрезка
тоже равна их сумме, параллельна им и приложена на середине отрезка 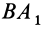 , т. е. в точке
, т. е. в точке 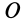 , где пересекаются диагонали прямоугольника
, где пересекаются диагонали прямоугольника 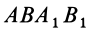 . Так как
. Так как 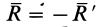 , то система сил
, то система сил 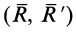 эквивалентна нулю и ее можно отбросить.
эквивалентна нулю и ее можно отбросить.
Таким образом, пара сил 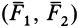 эквивалентна такой же паре сил
эквивалентна такой же паре сил 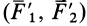 , но лежащей в другой, параллельной плоскости. Пару сил, не изменяя ее действия на твердое тело, можно перенести из одной плоскости в другую, параллельную ей.
, но лежащей в другой, параллельной плоскости. Пару сил, не изменяя ее действия на твердое тело, можно перенести из одной плоскости в другую, параллельную ей.
Векторный момент пары сил
Пару сил, приложенную к твердому телу, можно охарактеризовать плоскостью действия, моментом пары сил и направлением вращения пары. Все эти элементы пары сил в пространстве можно выразить одной величиной — векторным моментом пары сил.
Векторным моментом пары сил назовем вектор, числовое значение которого равно произведению силы пары на ее плечо. Векторный момент пары сил направлен перпендикулярно плоскости действия пары сил так, чтобы с его направления можно было видеть стремление пары сил вращать тело против часовой стрелки. Векторный момент пары сил условимся временно прикладывать посередине отрезка, соединяющего точки приложения сил пары (рис. 29). Его можно прикладывать также, как будет доказано ниже, в любой точке тела, _на которое действует пара сил. Векторный момент пары сил 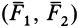 обозначим
обозначим 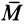 или
или 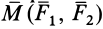 .
.
Согласно определению, числовое значение векторного момента пары сил 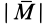 совпадает с модулем алгебраического момента пары сил и, следовательно,
совпадает с модулем алгебраического момента пары сил и, следовательно,
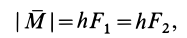
где 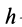 — плечо пары сил.
— плечо пары сил.
Векторный момент пары сил численно выражается площадью параллелограмма, построенного на силах пары:
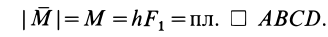
Отметим простейшие свойства векторного момента пары сил: его числовое значение не зависит от переноса сил пары вдоль своих линий действия, и он может быть равен нулю, если одна из сторон параллелограмма 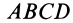 превратится в точку, т. е. плечо пары или сила пары становится равной нулю.
превратится в точку, т. е. плечо пары или сила пары становится равной нулю.
Векторный момент пары сил можно выразить в виде векторного произведения двух векторов:
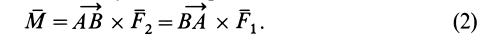
Действительно,
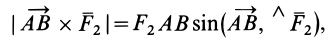
но
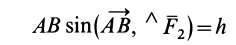
и, следовательно,
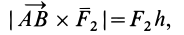
что совпадает с модулем векторного момента пары сил.
Направления векторных произведений 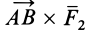 и
и 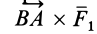 перпендикулярны плоскости, где лежат сомножители векторных произведений, а следовательно, и плоскости действия пары сил. Они совпадают с направлением векторного момента пары сил
перпендикулярны плоскости, где лежат сомножители векторных произведений, а следовательно, и плоскости действия пары сил. Они совпадают с направлением векторного момента пары сил 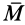 .
.
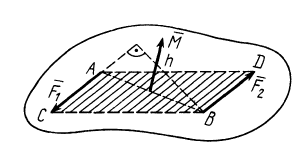
Рис. 29
Эквивалентность пар сил
Сформулируем условия эквивалентности двух пар сил, используя наиболее общую характеристику пары сил — ее векторный момент.
Известно, что пару сил можно как угодно поворачивать и переносить в плоскости ее действия; действие пары сил на твердое тело не изменяется, если алгебраический момент пары сил остается таким же. Следовательно, векторный момент пары сил можно переносить параллельно самому себе в любую точку твердого тела, лежащую в плоскости действия пары сил. Так как к тому же пару сил можно переносить в параллельную плоскость, то векторный момент пары сил можно переносить параллельно самому себе в любую точку тела, не изменяя действия пары сил на твердое тело. Поэтому векторный момент пары сил, действующей на твердое тело, есть свободный вектор, т. е. он характеризуется только модулем и направлением, а точкой приложения у него может быть любая точка тела; следовательно, векторный момент пары сил не обязательно прикладывать посередине отрезка, соединяющего точки приложения сил пары.
Итак, две пары сил, действующие на одно и то же твердое тело, эквивалентны, если они имеют одинаковые по модулю и направлению векторные моменты.
Теорема о сумме моментов сил пары
Сумма векторных моментов сил, входящих в состав пары, относительно любой точки не зависит от выбора точки и равна векторному моменту этой пары сил, т. е. для пары сил 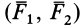
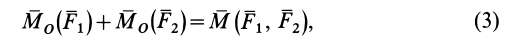
где 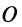 — любая точка (рис. 30).
— любая точка (рис. 30).
Эту теорему докажем, вычисляя левую часть равенства (3):
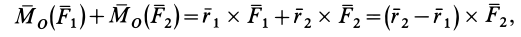
так как для пары сил
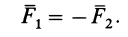
Но
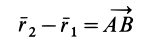
и не зависит от выбора точки 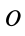 ; следовательно,
; следовательно,
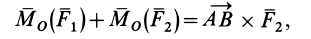
что на основании формулы (2) совпадает с векторным моментом пары сил 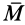 . Таким образом,
. Таким образом,
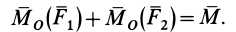
Взяв за точку 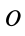 последовательно точки
последовательно точки 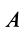 и
и 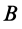 , по формуле (3) имеем
, по формуле (3) имеем
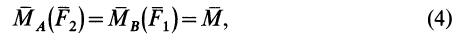
т. е. векторный момент пары сил равен векторному моменту одной из сил пары относительно точки приложения другой силы пары.
Эта теорема имеет важное значение при решении задач, когда надо вычислять сумму моментов сил пары относительно какой-либо точки. Для этого достаточно взять момент пары сил, что справедливо для любой точки.
Если моментная точка 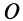 выбирается в плоскости действия сил пары как частный случай, справедлива теорема о сумме алгебраических моментов сил пары: сумма алгебраических моментов сил, входящих в состав пары сил, относительно точки, лежащей в плоскости действия пары сил, равна алгебраическому моменту пары сил и, следовательно, не зависит от выбора моментной точки, т. е.
выбирается в плоскости действия сил пары как частный случай, справедлива теорема о сумме алгебраических моментов сил пары: сумма алгебраических моментов сил, входящих в состав пары сил, относительно точки, лежащей в плоскости действия пары сил, равна алгебраическому моменту пары сил и, следовательно, не зависит от выбора моментной точки, т. е.
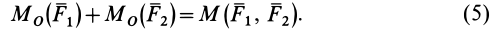
Выбирая 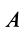 и
и 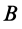 за моментные точки, лежащие на линиях действия сил пары, получаем
за моментные точки, лежащие на линиях действия сил пары, получаем
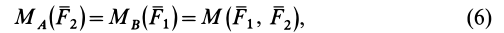
т. е. алгебраический момент пары сил равен алгебраическому моменту одной из сил пары относительно точки, лежащей на линии действия другой силы этой пары.
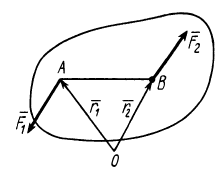
Рис. 30
Сложение пар сил
Рассмотрим случай, когда пары сил не лежат в одной или параллельных плоскостях, а расположены в пересекающихся плоскостях. Докажем, что две пары сил, действующие на одно и то же тело и лежащие в пересекающихся плоскостях, можно заменить одной эквивалентной парой сил, векторный Момент которой равен сумме векторных моментов заданных пар сил.
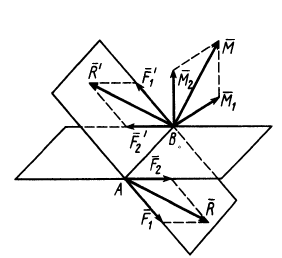
Рис. 31
Пусть имеются две пары сил 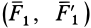 и
и 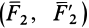 (рис.31), лежащие в пересекающихся плоскостях. Эти пары сил можно получить из пар сил, как угодно расположенных в пересекающихся плоскостях, путем параллельного переноса, поворота в плоскости действия и одновременного изменения плеч и сил пар. Сложим силы в точках
(рис.31), лежащие в пересекающихся плоскостях. Эти пары сил можно получить из пар сил, как угодно расположенных в пересекающихся плоскостях, путем параллельного переноса, поворота в плоскости действия и одновременного изменения плеч и сил пар. Сложим силы в точках 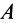 и
и 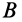 по правилу параллелограмма. После сложения получим две силы
по правилу параллелограмма. После сложения получим две силы 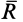 и
и 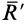 :
:
R = Fi 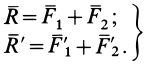 F2'> R' = F\+F'2.
F2'> R' = F\+F'2.
Силы 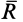 и
и 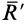 составляют пару сил, так как они приложены в разных точках и
составляют пару сил, так как они приложены в разных точках и 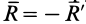 как равнодействующие равных, но противоположных сил, образующих пары сил.
как равнодействующие равных, но противоположных сил, образующих пары сил.
Итак, при сложении двух пар сил, лежащих в пересекающихся плоскостях, получается эквивалентная пара сил. Обозначим 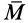 векторный момент пары сил
векторный момент пары сил 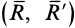 . Тогда на основании формул (4) и (7)
. Тогда на основании формул (4) и (7)
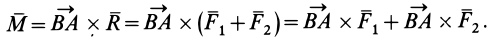
Учитывая, что
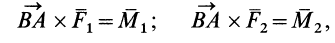
где 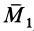 и
и 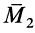 — векторные моменты заданных пар сил
— векторные моменты заданных пар сил 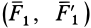 и
и 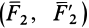 , имеем
, имеем
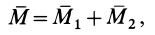
т. е. векторный момент эквивалентной пары сил равен сумме векторных моментов заданных пар.
Таким образом, чтобы сложить две пары сил, лежащие в пересекающихся плоскостях, надо сложить их векторные моменты по правилу параллелограмма в какой-либо точке тела, например в точке  (рис. 31). Сложение пар сил, лежащих в одной плоскости или параллельных плоскостях, есть частный случай сложения пар сил в пересекающихся плоскостях, так как в этом случае их векторные моменты параллельны и, следовательно, векторное сложение перейдет в алгебраическое.
(рис. 31). Сложение пар сил, лежащих в одной плоскости или параллельных плоскостях, есть частный случай сложения пар сил в пересекающихся плоскостях, так как в этом случае их векторные моменты параллельны и, следовательно, векторное сложение перейдет в алгебраическое.
Последовательно применяя правило параллелограмма ко всем векторным моментам пар сил, можно любое количество пар сил в общем случае заменить одной парой сил, векторный момент которой 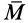 равен сумме векторных моментов заданных пар сил:
равен сумме векторных моментов заданных пар сил:
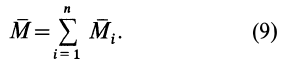
Если это сложение выполнять графически, особенно когда векторные моменты пар сил находятся в одной плоскости, то векторный момент эквивалентной пары сил изобразится замыкающей векторного многоугольника, построенного из векторных моментов заданных пар сил.
Для пар сил, расположенных в одной плоскости, теорема об их сложении формулируется так: пары сил, действующие на твердое тело и расположенные в одной плоскости, можно привести к одной паре сил, алгебраический момент которой равен сумме алгебраических моментов составляющих пар сил, т. е.

Так же складываются пары сил, расположенные в параллельных плоскостях, так как их предварительно можно перенести в одну плоскость.
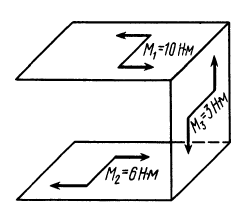
Рис. 32
Пример 1.
Определить векторный момент пары сил, которая получается при сложении двух пар сил с моментами 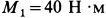 и
и 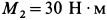 , действующих на одно и то же твердое тело. Пары сил расположены в пересекающихся плоскостях, двугранный угол между которыми равен
, действующих на одно и то же твердое тело. Пары сил расположены в пересекающихся плоскостях, двугранный угол между которыми равен 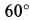 .
.
Решение. Складываем по правилу параллелограмма векторные моменты заданных пар сил. Для модуля векторного момента эквивалентной пары сил 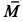 имеем
имеем
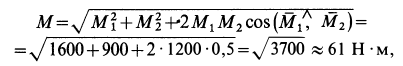
так как угол между 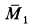 и
и 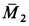 равен двугранному углу между плоскостями действия пар сил.
равен двугранному углу между плоскостями действия пар сил.
Пример 2.
Пары сил с моментами 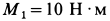 и
и 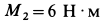 противоположного направления вращения находятся в параллельных плоскостях. Пара, имеющая момент
противоположного направления вращения находятся в параллельных плоскостях. Пара, имеющая момент 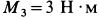 , расположена в перпендикулярной плоскости (рис. 32). Определить момент эквивалентной пары сил.
, расположена в перпендикулярной плоскости (рис. 32). Определить момент эквивалентной пары сил.
Решение. Сложим сначала алгебраически моменты пар сил, расположенных в параллельных плоскостях. Получим пару сил с моментом 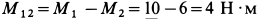 , так как моменты пар сил имеют противоположные знаки. Пару сил с моментом
, так как моменты пар сил имеют противоположные знаки. Пару сил с моментом 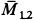 сложим с парой сил, имеющей момент
сложим с парой сил, имеющей момент 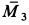 . Так как угол между
. Так как угол между 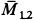 и
и 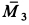 прямой, то момент эквивалентной пары
прямой, то момент эквивалентной пары
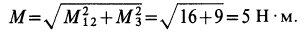
Условия равновесия пар сил
Если на твердое тело действуют пары сил, как угодно расположенные в пространстве, то эти пары сил можно заменить одной эквивалентной парой сил, векторный момент которой равен сумме векторных моментов заданных пар сил, т. е.
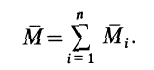
Векторный момент 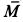 геометрически изображается замыкающей векторного многоугольника, построенного на векторных моментах заданных пар сил.
геометрически изображается замыкающей векторного многоугольника, построенного на векторных моментах заданных пар сил.
Для равновесия пар сил, действующих на твердое тело, необходимо и достаточно, чтобы модуль векторного момента эквивалентной пары сил был равен нулю или чтобы векторный многоугольник, построенный на векторных моментах заданных пар сил, был замкнут.
Итак, 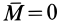 . Отсюда
. Отсюда
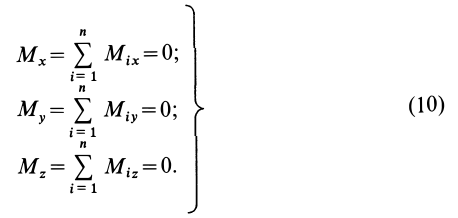
Таким образом, для равновесия пар сил, приложенных к твердому телу, необходимо и достаточно, чтобы алгебраическая сумма проекций векторных моментов пар сил на каждую из трех координатных осей была равна нулю.
В общем случае пары сил можно уравновесить только парой сил и нельзя уравновесить одной силой или какой-либо другой системой сил, отличной от пары сил.
В том случае, когда пары сил действуют на твердое тело, находясь в одной плоскости, их можно заменить одной эквивалентной парой сил, алгебраический момент которой равен сумме алгебраических моментов составляющих пар сил:
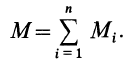
Для равновесия таких пар сил необходимо и достаточно, чтобы алгебраический момент эквивалентной им пары сил был равен нулю, т. е. для равновесия пар сил, действующих на твердое тело в одной плоскости, необходимо и достаточно, чтобы сумма алгебраических моментов этих пар сил была равна нулю.
Если на твердое тело действуют только пары сил, лежащие в одной плоскости, то реакции опор, уравновешивающие заданные пары сил, составляют пару сил. Например, если одной из двух опор тела в его точке 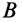 является катковая опора (рис. 33), а другой — неподвижный шарнир в точке
является катковая опора (рис. 33), а другой — неподвижный шарнир в точке 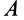 , то направление реакции в шарнире
, то направление реакции в шарнире 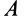 противоположно направлению реакции в точке
противоположно направлению реакции в точке 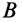 , так как эти реакции составляют пару сил. Реакция катковой опоры
, так как эти реакции составляют пару сил. Реакция катковой опоры 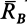 перпендикулярна плоскости опоры катков и направлена вверх; следовательно,
перпендикулярна плоскости опоры катков и направлена вверх; следовательно, 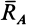 направлена параллельно
направлена параллельно 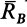 вниз.
вниз.
Величины этих реакций равны. Их можно найти приравняв момент пары сил опорных реакций сумме алгебраических моментов пар сил, действующих на тело. Таким образом,
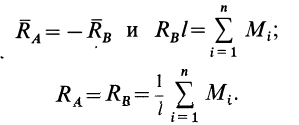
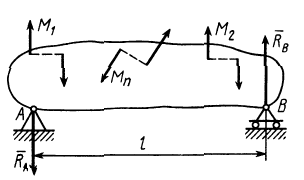
Рис. 33
Теория пар, расположенных в одной плоскости
При сложении двух параллельных сил  и
и 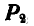 , направленных в разные стороны (рис. 35), может оказаться, что
, направленных в разные стороны (рис. 35), может оказаться, что 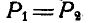 ; в этом случае равнодействующая таких сил
; в этом случае равнодействующая таких сил 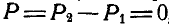 а ее точка приложения С, определяемая одним из равенств:
а ее точка приложения С, определяемая одним из равенств:
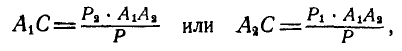
находится в бесконечности.
Поэтому силы 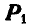 и
и 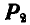 не могут быть заменены одной равнодействующей силой. Такая система двух равных параллельных сил Р и —Р, направленных в противоположные стороны, называется парой сил (рис. 37). Расстояние р между линиями действия сил Р и —Р называется плечом пары, а произведение одной из сил пары на плечо — моментом пары, который равен:
не могут быть заменены одной равнодействующей силой. Такая система двух равных параллельных сил Р и —Р, направленных в противоположные стороны, называется парой сил (рис. 37). Расстояние р между линиями действия сил Р и —Р называется плечом пары, а произведение одной из сил пары на плечо — моментом пары, который равен:
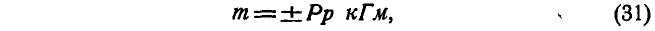
где знак плюс берется, если пара поворачивает плоскость чертежа по направлению против часовой стрелки, а знак минус — по часовой стрелке. Будем изображать пару так, чтобы начало каждой из сил совпадало с концами плеча пары (рис. 38).

Рис. 37. Рис. 38.
Пары сил имеют следующие свойства:
- Пару сил нельзя заменить равнодействующей силой, а следовательно, и уравновесить силой; действие пары определяется ее моментом.
- Равновесие тела не нарушается при переносе пары в любое положение в ее плоскости.
Дана пара  с плечом АВ (рис. 39). Пусть повернуто плечо пары АС. Прикладывая к точкам А и С четыре равные и взаимно уравновешивающиеся силы
с плечом АВ (рис. 39). Пусть повернуто плечо пары АС. Прикладывая к точкам А и С четыре равные и взаимно уравновешивающиеся силы 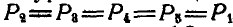 , перпендикулярные к АС, находим равнодействующие
, перпендикулярные к АС, находим равнодействующие 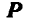 и
и 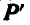 сил
сил 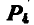 и
и 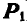 , а также
, а также 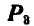 и
и 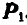 .
.
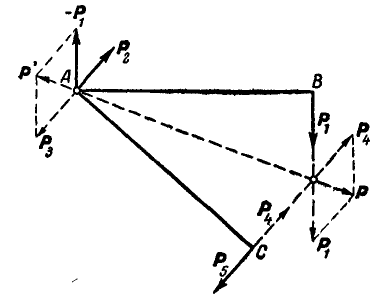
Рис. 39.
Равнодействующие Р и Р' равны между собой и направлены по одной прямой, так как делят пополам углы соответствующих ромбов. На основании изложенного заключаем, что силы 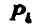 и
и 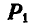 , а также
, а также 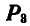 и
и 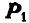 попарно уравновешиваются. Удаляя их, поручаем пару
попарно уравновешиваются. Удаляя их, поручаем пару  с плечом АС, эквивалентную заданной паре. Этим мы доказали, что пару можно повернуть на любой угол. Отсюда делаем вывод, что пару можно также перенести в ее плоскости в любое положение, так как перенос пары можно осуществить рядом ее поворотов.
с плечом АС, эквивалентную заданной паре. Этим мы доказали, что пару можно повернуть на любой угол. Отсюда делаем вывод, что пару можно также перенести в ее плоскости в любое положение, так как перенос пары можно осуществить рядом ее поворотов.
3. При изменении величин сил и длин плеч двух пар эти пары остаются статически эквивалентными, если их момент при этом сохраняет свою величину и знак.
Пусть дана пара  с плечом АВ (рис. 40). Разлагаем силу
с плечом АВ (рис. 40). Разлагаем силу 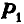 на две силы
на две силы 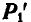 и
и 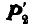 из которых
из которых 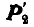 приложена к точке А, a
приложена к точке А, a 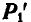 — к неизвестной пока точке С на прямой АВ. Так как
— к неизвестной пока точке С на прямой АВ. Так как 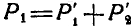 и
и 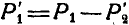 , то силы
, то силы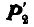 и
и 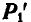 , приложенные в точке A, заменяем силой
, приложенные в точке A, заменяем силой 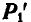 . Отсюда следует, что пару
. Отсюда следует, что пару 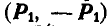 мы заменили парой
мы заменили парой  , эквивалентной данной, так как из равенств
, эквивалентной данной, так как из равенств 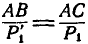 и
и 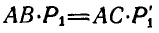 заключаем, что моменты указанных пар равны между собой. Следовательно, две пары, лежащие в одной плоскости, эквивалентны, если они имеют равные моменты и одинаковое направление вращения.
заключаем, что моменты указанных пар равны между собой. Следовательно, две пары, лежащие в одной плоскости, эквивалентны, если они имеют равные моменты и одинаковое направление вращения.
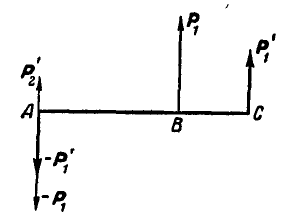
Рис. 40.
4. Для пар, расположенных в равнодействующей пары равен алгебраической сумме моментов пар составляющих.
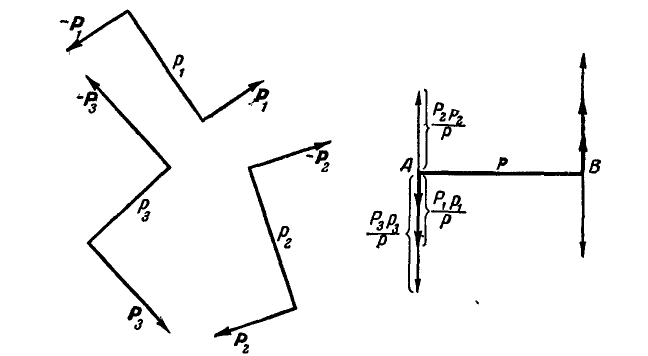
Рис. 41.
Если имеются, например, три пары (рис. 41) с неодинаковыми плечами, то, задавшись плечом р, одинаковым для всех пар, получаем силы пар, получаем силы пар равными 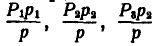 .
.
Совместив затем плечи всех пар, получаем одну пару с силами 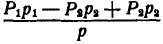 . Момент
. Момент 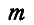 этой пары равен:
этой пары равен:
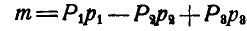 .
.
Вообще, если имеется 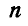 пар, то можем написать:
пар, то можем написать:
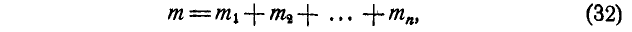
где 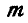 —момент равнодействующей пары;
—момент равнодействующей пары;
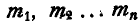 — моменты составляющих пар.
— моменты составляющих пар.
5. Пары, взаимно уравновешиваются, если алгебраическая сумма моментов их равна нулю.
Это следует из того, что при сложении сил в точках А и В (рис. 41) сумма их может оказаться равной нулю, а потому и момент равнодействующей пары также будет равен нулю.
Полагая в уравнении (32) 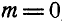 , получим условие равновесия пар на плоскости:
, получим условие равновесия пар на плоскости:
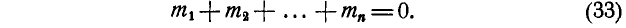
Задача с решением
На свободную жесткую систему ABCD (рис. 42) действуют четыре
силы и плечи которых соответственна равны:
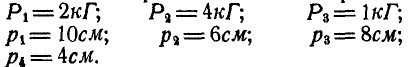
Определить величину и направление сил 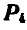 и
и 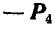 четвертой пары так, чтобы система находилась в равновесии.
четвертой пары так, чтобы система находилась в равновесии.
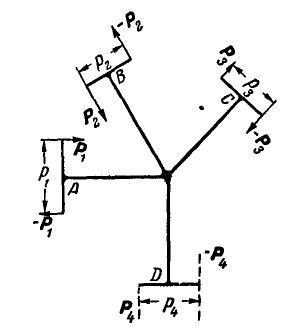
Рис. 42.
Решение. Применим уравнение (33) равновесия пар:
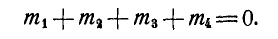
Выражая моменты пар через произведения сил и плеч, имеем:
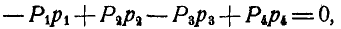 или
или 
откуда 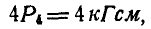 т. е. искомая пара будет стремиться повернуть систему по направлению часовой стрелки, а каждая из неизвестных сил пары
т. е. искомая пара будет стремиться повернуть систему по направлению часовой стрелки, а каждая из неизвестных сил пары 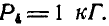
| Рекомендую подробно изучить предмет: |
| Ещё лекции с примерами решения и объяснением: |