
Теория пар, не лежащих в одной плоскости в теоретической механике
Теория пар, не лежащих в одной плоскости:
Пусть дана пара сил (Р,— Р), действующая в плоскости V, расположенной как угодно в пространстве (рис. 107).
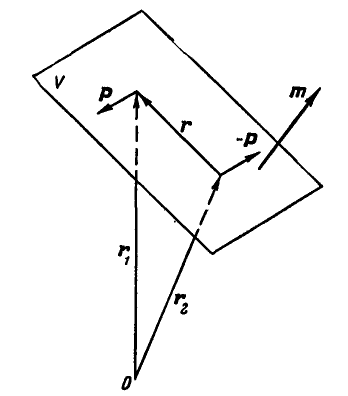
Рис. 107.
Вычислим сумму моментов 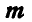
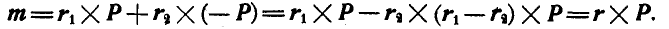
Отсюда следует, что момент пары не зависит от положения тонки О и представляет собой вектор, направленный перпендикуляр но к плоскости действия пары в такую сторону, чтобы, смотря с конца стрелки этого вектора, вращение пары представлялось происходящим против часовой стрелки.
Модуль этого вектора: 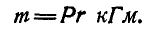
Покажем теперь, что пару сил можно переносить параллельно самой себе.
Пусть имеется пара (Р, — Р) с плечом АВ, расположенная в плоскости  (рис. 108). Возьмем любую плоскость
(рис. 108). Возьмем любую плоскость  , параллельную
, параллельную , с отрезком CD, равным и параллельным АВ, и приложим в точках С и D взаимно-уравновешивающиеся силы Р и —Р.
, с отрезком CD, равным и параллельным АВ, и приложим в точках С и D взаимно-уравновешивающиеся силы Р и —Р.
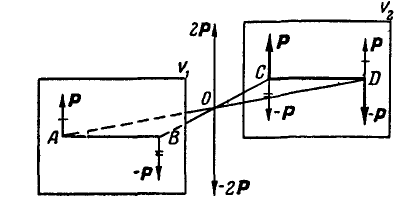
Рис. 108.
Соединяя точки С с В и А с D, замечаем, что AO=OD и ВО=ОС в силу свойств диагоналей параллелограмма; поэтому в результате сложения параллельных сил, отчеркнутых один раз и два раза, получаем силы 2Р и —2Р, взаимно уравновешивающиеся; данная нам пара оказалась перенесенной в плоскость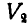 .
.
Отсюда следует, что момент пары является вектором свободным и его можно переносить в любую точку твердого тела параллельно самому себе.
При сложении пар в пространстве могут встретиться два случая.
- 1. Пары расположены в параллельных плоскостях. В этом случае все пары можно' перенести в одну плоскость и сложить их моменты алгебраически (см. § 8).
- 2. Пары расположены в пересекающихся плоскостях. Рассмотрим сначала случай сложения двух пар (рис. 109). Приведя пары, расположенные в плоскостях
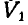 , и
, и 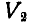 к одному плечу
к одному плечу 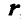 , перенесем их затем так, чтобы их плечи совпадали с линией пересечения плоскостей.
, перенесем их затем так, чтобы их плечи совпадали с линией пересечения плоскостей.
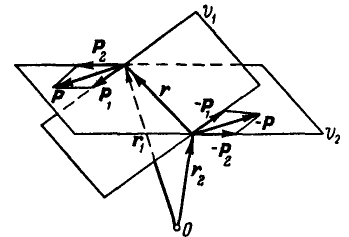
Рис. 109.
Складывав затем силы перенесенных пар 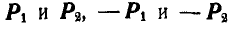 по правилу параллелограмма, имеем:
по правилу параллелограмма, имеем:
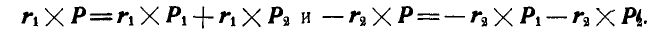
Складывая почленно полученные равенства, найдем:
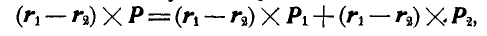
откуда
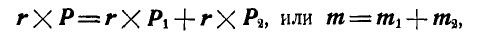
т. е. момент равнодействующей, пары равен геометрической сумме моментов пар составляющих. Если имеется 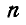 пар, расположенных как угодно в пространстве, то
пар, расположенных как угодно в пространстве, то
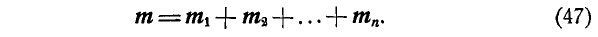
Может оказаться, что 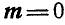 ; в этом случае многоугольник моментов пар будет замкнут и пары будут взаимно уравновешиваться, а поэтому
; в этом случае многоугольник моментов пар будет замкнут и пары будут взаимно уравновешиваться, а поэтому
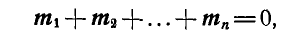
т. е. пары расположенные как угодно в пространстве, взаимно уравновешиваются, если их геометрическая сумма моментов равна нулю.
Задача:
На вал MN перпендикулярно к его оси насажены четыре шкива, радиусы которых соответственно равны 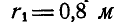 ,
, 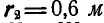 ,
, 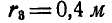 и
и 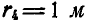 (рис. 110). К ободьям шкивов I, II и III приложены пары, направление вращения которых показано на чертеже. Каковы должны быть величина и направление сил, приложенных к ободу шкива IV, чтобы вал находился в равновесии, если
(рис. 110). К ободьям шкивов I, II и III приложены пары, направление вращения которых показано на чертеже. Каковы должны быть величина и направление сил, приложенных к ободу шкива IV, чтобы вал находился в равновесии, если 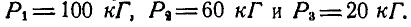
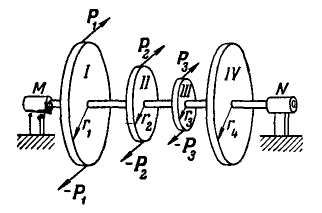
Рис. 110.
Решение. Пары расположены в параллельных плоскостях, поэтому по формуле (33) имеем: 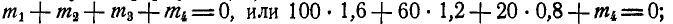 откуда
откуда 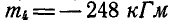 ; так как
; так как 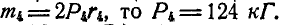
Направление же вращения пары  обратно направлению вращения данных пар.
обратно направлению вращения данных пар.
Задача:
Найти момент равнодействующей пары т четырех пар (рис. 111, а), линии действия сил которых совпадают с ребрами куба. Известно, что сторона куба 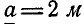 и
и 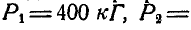
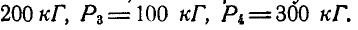
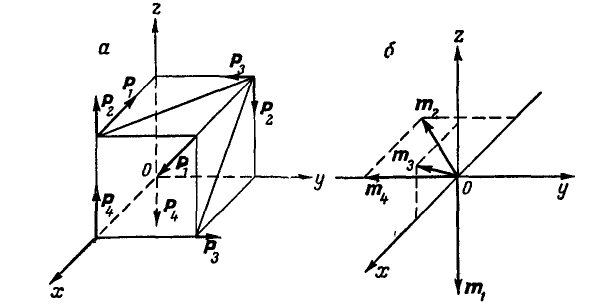
Рис. 111.
Решение. Перенесем моменты всех пар в любую точку О (рис. 111, б) и вычислим их модули
Проекции момента равнодействующей пары на координатные оси найдем по формуле (3):
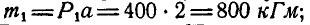
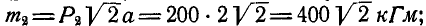
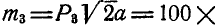
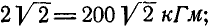
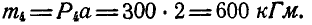
Проекции момента равнодействующей пары на координатные оси найдем по формуле (3):
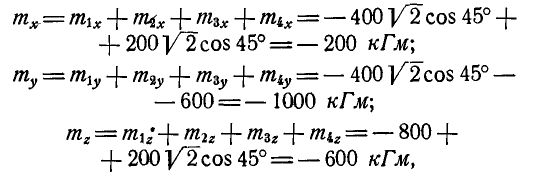
откуда 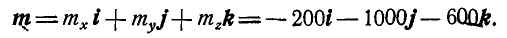
| Рекомендую подробно изучить предмет: |
| Ещё лекции с примерами решения и объяснением: |
- Произвольная пространственная система сил
- Центр параллельных сил и центр тяжести
- Поступательное движение твердого тела
- Вращение твердого тела вокруг неподвижной оси
- Графостатика в теоретической механике
- Расчет ферм
- Пространственная система сходящихся сил
- Момент силы относительно точки и относительно оси