
Теоремы синусов и косинусов - определение и вычисление с примерами решения
Содержание:
Теоремы синусов и косинусов
Теорема косинусов
Живший в XII веке и занимающий особое место в истории человечества великий азербайджанский учёный Насреддин Туси сделал особый вклад в астрономию, математику и философию. Насреддин Туси, впервые отделил тригонометрию от астрономии, и представил доказательство теоремы синусов. 
Теорема синусов
Для произвольного 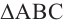 со сторонами а, b, с и соответствующими противолежащими углами
со сторонами а, b, с и соответствующими противолежащими углами 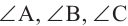 имеет место:
имеет место:
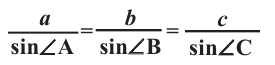
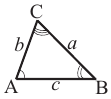
Стороны треугольника пропорциональны синусам противолежащих углов. Доказательство: Справедливость теоремы для прямоугольного треугольника покажите самостоятельно. Докажем теорему для остроугольного и тупоугольного треугольников.
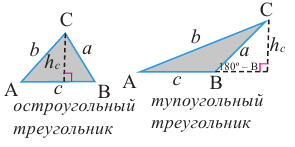
Из вершины С треугольника проведём к стороне АВ высоту 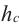 . Получим два прямоугольных треугольника, для которых имеем
. Получим два прямоугольных треугольника, для которых имеем 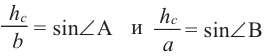 .
.
Из тупоугольного треугольника имеем: 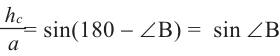 . Найдём из этих отношений:
. Найдём из этих отношений: 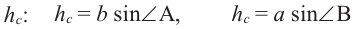
Отсюда получаем, что: 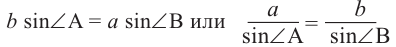 .
.
По аналогичному правилу, если провести высоту из вершины угла А
на сторону ВС, то можно показать, что 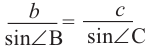
По свойству равенства имеем:

Следствия.
1)В треугольнике, напротив равных углов лежат стороны, длины которых равны.
2)В треугольнике напротив большего угла лежит большая сторона, а напротив большей стороны лежит больший угол.
На самом деле, для острых углов 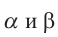 , если
, если 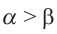 , то
, то 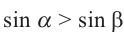 .
.
Так как 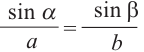 , то
, то 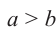 .Для тупого угла
.Для тупого угла 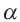 угол (180° -
угол (180° -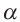 )
)
является острым, а также угол (180° - 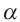 ) является внешним углом треугольника не смежными с углом
) является внешним углом треугольника не смежными с углом 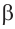 и больше него.
и больше него.
Поэтому, 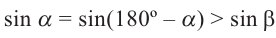 . Отсюда снова получаем, что
. Отсюда снова получаем, что 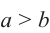 . Если для треугольника заданы два угла и одна сторона, две стороны и угол, противолежащий одной из сторон, то применив теорему синусов, можно найти остальные стороны и углы.
. Если для треугольника заданы два угла и одна сторона, две стороны и угол, противолежащий одной из сторон, то применив теорему синусов, можно найти остальные стороны и углы.
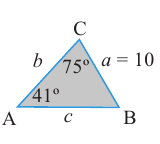
I случай. Даны два угла и одна сторона треугольника.
Пример 1.В 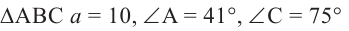
Решение: Зная, что сумма внутренних углов треугольника равна 180°, по двум заданным углам найдём третий, а по теореме синусов неизвестные стороны. 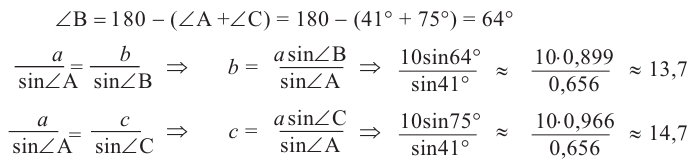
II случай. Даны две стороны и угол, противолежащей одной из сторон.
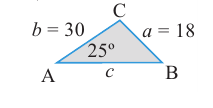
Пример 2. 1)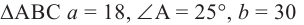
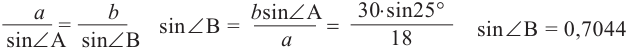
Введём число 0,7044 в калькулятор и нажмём кнопку со знаком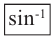 . Увидим, что угол В равен 44,8°:
. Увидим, что угол В равен 44,8°: 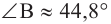
Однако, зная, что 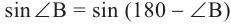 , тогда получается, что у угла В есть ещё второе значение:
, тогда получается, что у угла В есть ещё второе значение: 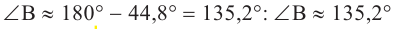
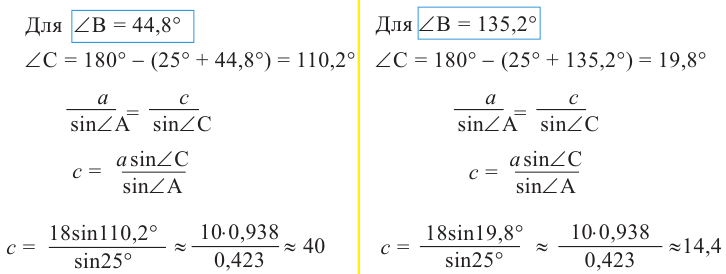
Таким образом, для заданных значений существует два треугольника. 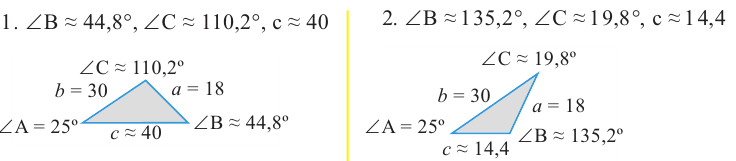
Рассмотрим для II случая следующую ситуацию.
Пусть в 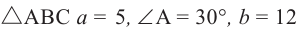
По теореме синусов 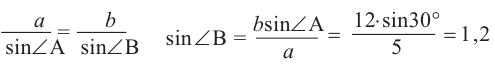
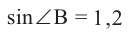 Так как
Так как 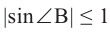
то он не может принимать значение 1,2.
Значит, такой треугольник не существует.
Количество возможных решений треугольников по двум сторонам и одному углу может меняться в зависимости от значений длины сторон и вида угла (градусной меры). 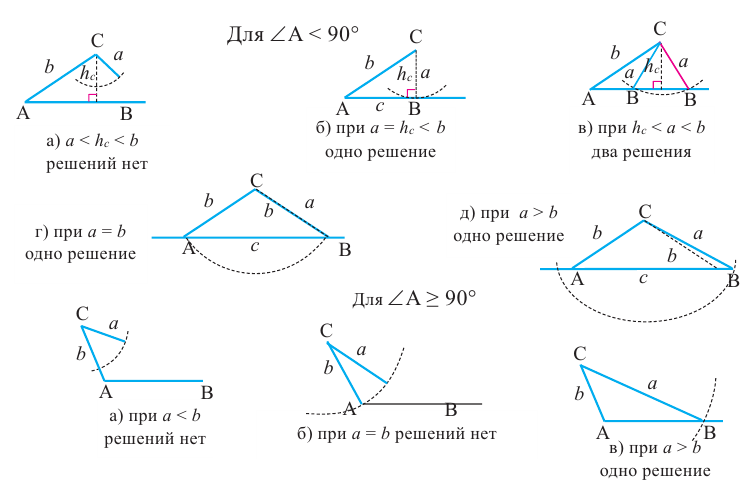
Пример. Водохранилище находится от комплекса 4-ая Вершина на расстоянии 15 км по направлению на северо-запад под углом 25 . Комплекс Гянджилик находится на расстоянии 7,5 км в направлении на северо-восток от комплекса 4-ая Вершина. Найдите расстояние от Гянджилика до водохранилища.
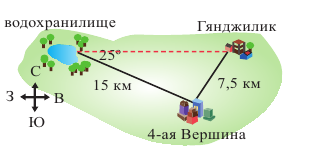
Решение: Согласно плану изобразим треугольник, вершинам которого соответствуют буквы объектов: водохранилище - S, 4-ая Вершина - Т, Гянджилик -G.
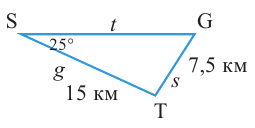
Соответствующие расстояния обозначим буквами 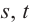 и
и 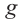 .
.
По теореме синусов:
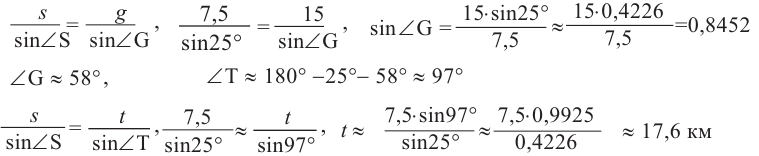
Теорема косинусов
Исследование 1. Выполните следующие задания для каждого треугольника с заданными размерами:
1) Запишите углы треугольника в порядке возрастания.
2) Можно ли найти неизвестные стороны или углы применив теорему синусов? 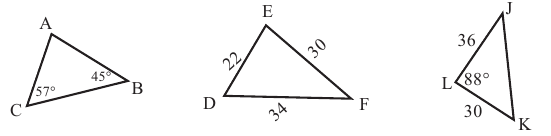
Исследование 2.
1)В тетради изобразите треугольники по двум сторонам и углу между ними и измерьте третью сторону, согласно следующим данным.

2)Для полученных треугольников заполните таблицу.

3)Сравните значения выражений 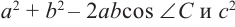 .
.
Теорема косинусов
Для произвольного треугольника ABC со сторонами a, b и с .

Квадрат стороны треугольника равен сумме квадратов двух других сторон, минус удвоенное произведение этих сторон на косинус угла между сторонами. Доказательство: Для доказательства теоремы косинусов расположим треугольник ABC в координатной плоскости так, чтобы вершина А совпадала с началом координат. В этом случае координаты вершин равны: 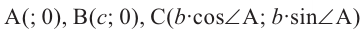 . По формуле расстояния между двумя точками:
. По формуле расстояния между двумя точками:
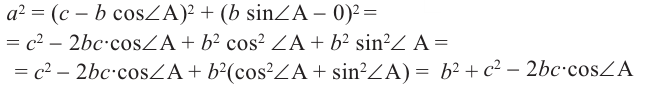
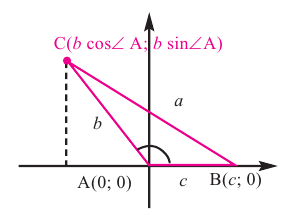
Таким образом, мы доказали, что: 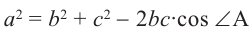 . Доказать эту формулу для других сторон, можно расположив другие вершины (В и С) в начале координат.
. Доказать эту формулу для других сторон, можно расположив другие вершины (В и С) в начале координат.
Замечание: Пусть 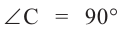 . Так как
. Так как 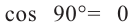 ,то формула
,то формула 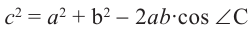 будет выглядеть так:
будет выглядеть так: 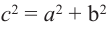 , т.е. выражает теорему Пифагора. Поэтому теорему косинусов называют обобщённой теоремой Пифагора
, т.е. выражает теорему Пифагора. Поэтому теорему косинусов называют обобщённой теоремой Пифагора
Пример 1. Решение треугольника по двум сторонам и углу между ними.
Решите треугольник, если в 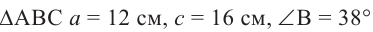 .
.
Решение.

Если известны три стороны и один из углов треугольника, то можно применить теорему синусов. Найдём угол А. Известно, если сторона а меньше стороны с, то угол напротив этой стороны также будет меньшим, то есть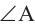 не может быть тупым.
не может быть тупым. 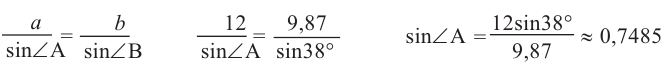
Нажмите кнопку 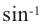 на калькуляторе и введите число 0,7485, тогда можно найти
на калькуляторе и введите число 0,7485, тогда можно найти 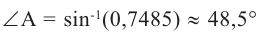 . Теперь, для треугольника ABC известны три стороны и два угла. Третий угол можно найти из формулы суммы внутренних углов треугольника:
. Теперь, для треугольника ABC известны три стороны и два угла. Третий угол можно найти из формулы суммы внутренних углов треугольника:
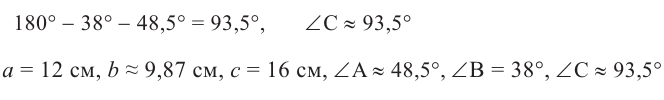
Пример 2. Решим треугольник по трём сторонам. В  а = 5 см, b = 8 см, с = 12 см.
а = 5 см, b = 8 см, с = 12 см.
Решение.
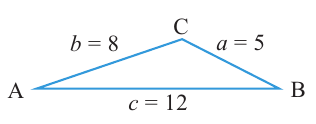
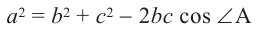
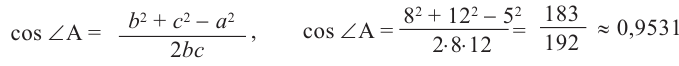
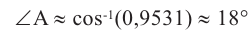
Пример. Поезд прошёл путь 60 км из пункта А в пункт С. После чего он изменил направление на 15° и прошёл ещё 80 км до пункта В. На сколько километров удалился поезд от пункта А?
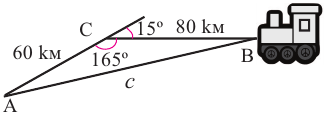
Решение: Изобразим решение задачи. По рисунку видно, что в треугольнике известны две стороны и угол между ними. Сторону с можно найти по теореме косинусов: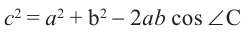
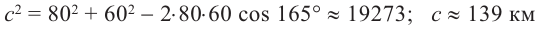
| Рекомендую подробно изучить предметы: |
| Ещё лекции с примерами решения и объяснением: |