Теоремы об изменении количества движения и о движении центра масс в теоретической механике

Содержание:

Количество движения точки и системы:

Одной из мер движения точки или системы является количество их движения.

Количеством движения материальной точки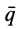

Количество движения точки в физике часто называют импульсом материальной точки.

Проекции количества движения точки на прямоугольные декартовы оси координат:

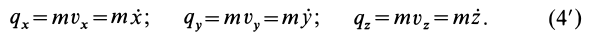
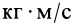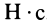Размерность количества движений в СИ — или . Количеством движения системы 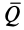называют векторную сумму количеств движений отдельных точек систем, т. е.

и, следовательно, проекции количества движения системы на прямоугольные декартовы оси координат

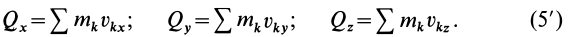
Вектор количества движения системы 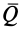в отличие от вектора количества движения точки 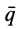не имеет точки приложения. Вектор количества движения точки считается приложенным в самой движущейся материальной точке, а вектор 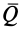является свободным вектором.

Вычисление количества движения системы

Количество движения системы можно выразить через массу системы 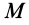и скорость центра масс :

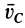В проекциях на прямоугольные декартовы оси соответственно

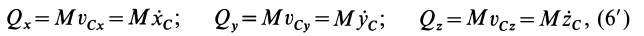
где 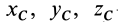— координаты центра масс системы. Выведем формулу (6):

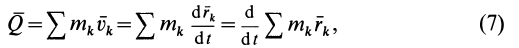
где 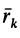— радиус-вектор 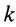-й точки системы (рис. 40).

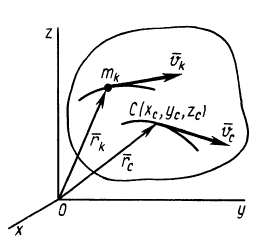
Рис. 40

По формуле для радиуса-вектора центра масс,

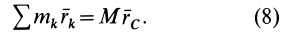
Подставляя значение статического момента массы (8) в (7), имеем

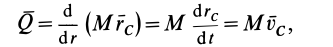
так как масса системы 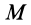не изменяется при движении системы. 

Элементарный и полный импульсы силы

Действие силы 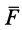на материальную точку в течение времени 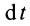можно охарактеризовать так называемым элементарным импульсом силы 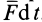.  Полный импульс силы 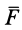за время 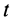, или импульс силы 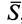, определяют по формуле

Проекции импульса силы на прямоугольные оси координат выражаются формулами

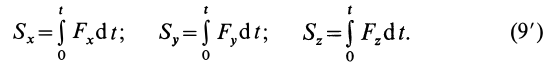
Единица импульса силы — .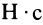

Теорема об изменении количества движения точки

Дифференциальное уравнение движения материальной точки под действием силы 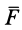можно представить в следующей векторной форме:

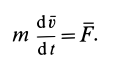
Так как масса точки 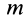принята постоянной, то ее можно внести под знак производной. Тогда

Формула (10) выражает теорему об изменении количества движения точки в дифференциальной форме: первая производная по времени от количества движения точки равна действующей на точку силе.

В проекциях на координатные оси (10) можно представить в виде

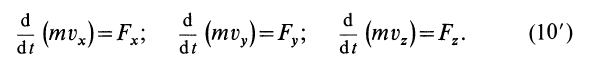
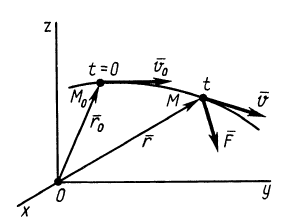
Рис. 41

Если обе части (10) умножить на 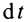, то получим другую форму этой же теоремы — теорему импульсов в дифференциальной форме:

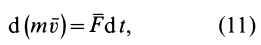
т. е. дифференциал от количества движения точки равен элементарному импульсу силы, действующей  на точку.

Проецируя обе части (11) на координатные оси, получаем

Интегрируя обе части (11) в пределах от нуля до 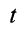(рис. 41), имеем

где 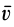 — скорость точки в момент 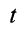; 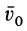— скорость при 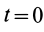;  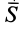—импульс силы за время .

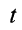Выражение в форме (12) часто называют теоремой импульсов в конечной (или интегральной) форме: изменение количества движения точки за какой-либо промежуток времени равно импульсу силы за тот же промежуток времени. В проекциях на координатные оси эту теорему можно представить в следующем виде:

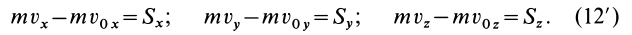
Для материальной точки теорема об изменении количества движения в любой из форм, по существу, не отличается от дифференциальных уравнений движения точки.

Теорема об изменении количества движения системы

Аналогично тому, как для одной материальной точки, выведем теорему об изменении количества движения для системы в различных формах. Пусть к точкам системы приложены внешняя и внутренняя силы. Тогда для каждой точки можно применить теорему об изменении количества движения, например в форме (10) (см. рис. 40):

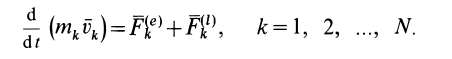
Суммируя по всем точкам системы правые и левые части этих соотношений и учитывая, что сумма производных равна производной от суммы, получаем

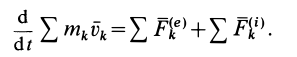
Так как, по свойству внутренних сил и определению количества движения системы,

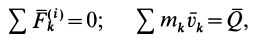
то приведенное соотношение можно представить в виде

Выражение (13) является теоремой об изменении количества движения системы в дифференциальной форме: производная по времени от количества движения системы равна векторной сумме всех внешних сил, действующих на систему. В проекциях на прямоугольные декартовы оси координат

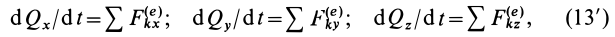
т. е. производная по времени от проекции количества движения системы на какую-либо координатную ось равна сумме проекций всех внешних сил системы на ту же ось.

Умножая обе части (13) на 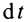, получаем теорему импульсов для системы в дифференциальной форме:

т. е. дифференциал количества движения системы равен векторной сумме элементарных импульсов всех внешних сил, действующих на систему. В проекциях на координатные оси эта теорема примет вид

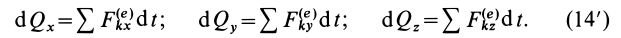
Вычисляя интегралы от обеих частей (14) по времени- от нуля до получаем теорему импульсов для системы в конечной или интегральной форме:

где 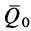— количество движения системы в момент 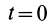;  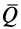 — количество движения в момент 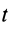; 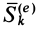— импульс внешней силы, действующей на 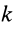-ю точку за время ; .

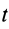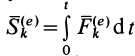Теорема импульсов для системы в конечной форме формулируется так: изменение количества движения системы за какое-либо время равно векторной сумме всех импульсов внешних сил, действующих на систему за то же время. В проекциях на прямоугольные оси согласно (15) имеем:

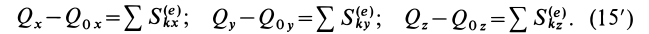
Внутренние силы системы не входят явно в теорему об изменении количества движения системы в любой из форм и, следовательно, не влияют непосредственно на изменение количества движения системы. Они могут влиять на изменение количества движения только неявно через внешние силы.

Из теоремы об изменении количества движения для точки и системы при некоторых условиях для внешних сил можно получить так называемые первые интегралы системы дифференциальных уравнений точки и системы. Эти первые интегралы называют законами сохранения количества движения или проекции количества движения на ось. Рассмотрим эти законы сохранения для точки и системы одновременно, считая материальную точку механической системой, состоящей из одной точки.

Законы сохранения количества движения

Законы сохранения количества движения системы получаются как частные случаи теоремы об изменении количества движения для системы в зависимости от особенностей системы внешних сил, приложенных к рассматриваемой механической системе, а для одной точки — от особенностей сил, действующих на точку. Внутренние силы при этом могут быть любыми, так как они явно не влияют на изменение количества движения системы.

Возможны два частных случая.

1.    Если векторная сумма всех внешних сил, приложенных к системе, равна нулю, т. е. 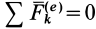, то из теоремы об изменении количества движения системы, например в форме (13), следует, что

Этот закон (точнее, частный случай теоремы) формулируется так: если главный вектор внешних сил системы равен нулю, то количество движения системы постоянно по величине и направлению. В проекциях на координатные оси, по этому закону,

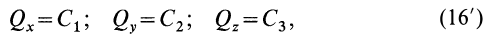
где 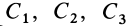— постоянные величины.

В соотношения (16) и (16') входят производные от координат точек по времени не выше первого порядка и не входят вторые производные от этих координат. Следовательно, эти соотношения являются первыми интегралами дифференциальных уравнений системы (3).

2.    Если равна нулю проекция главного вектора внешних сил на какую-либо координатную ось 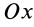, т. е. 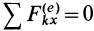, то из (13') имеем

Выражение (17) является законом сохранения проекции количества движения системы: если проекция главного вектора всех внешних сил системы на какую-либо ось равна нулю, то проекция количества движения на ту же ось является постоянной величиной.

Применим закон сохранения количества движения системы для объяснения принципа реактивного движения. Пусть, например, система состоит из двух сочлененных твердых тел, находящихся в покое и свободных от действия внешних сил. Тогда для рассматриваемой системы количество движения все время постоянно и равно нулю. Допустим, что при взрыве пиропатрона (действие внутренних сил) первому телу массой 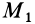сообщена скорость 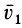. Тогда скорость второго тела массой  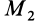определится из закона сохранения количества движения

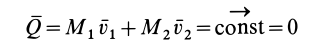
Следовательно,

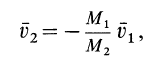
т. е. второе тело движется в сторону, противоположную первому телу. Если его движению препятствует какая-либо связь, то рассматриваемое тело давит на эту связь с некоторой силой по направлению скорости 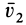. Эту силу называют реактивной. В реактивных двигателях она создается за счет истечения газа с большой скоростью (около 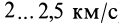) из сопла двигателя.

Теорему об изменении количества движения в той или другой форме удобно применять для решения задач именно в рассмотренных частных случаях, хотя в некоторых случаях ее применяют и в общем случае. Отметим, что внутренние силы не влияют на изменение количества движения в изолированных системах, т. е. в системах, которые не соприкасаются с другими телами, не принадлежащими к рассматриваемой системе, или окружающей систему материальной средой.

В неизолированных механических системах внутренние силы, вызывая движение отдельных частей системы вследствие взаимодействия с внешними телами или окружающей материальной средой, могут вызвать внешние силы в виде сил реакций связей или изменения активных сил, которые могут изменить количество движения системы.

Количество движения системы может зависеть от внутренних сил только неявно, через внешние силы.

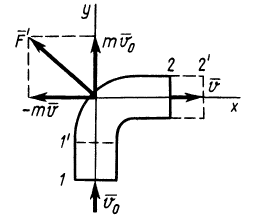
Рис. 42

Пример №1

Через изогнутую под прямым углом трубу постоянного сечения за 1 с протекает жидкость массой 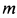(рис. 42). Скорость течения жидкости 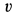постоянна, т. е. одна и та же у всех частиц жидкости. Определить силу, с которой жидкость давит на участок трубы вследствие поворота потока на прямой угол.

Решение:

Применим к объему жидкости, заключенному между стенками трубы и поперечными сечениями 1 и 2, теорему об изменении количества движения в форме теоремы импульсов за промежуток времени, равный 1 с. За секунду точки жидкости из сечения 1 сместятся на расстояние 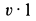и займут положение 1', а точки жидкости из сечения 2 займут положение 2'. По теореме импульсов для выделенного объема жидкости имеем

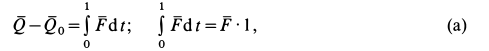
где 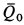— количество движения жидкости, заключенной между сечениями 1 и 2; 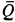— количество движения жидкости, заключенной между сечениями 1' и 2'; 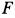—главный вектор распределенных сил, с которыми стенки трубы действуют на выделенный объем жидкости.

Так как в общей части объема жидкости количества движения, входящие в 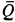и 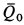, взаимно уничтожаются при их вычитании, то из (а) получаем

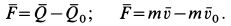
Сила давления жидкости 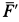на стенки трубы по закону о равенстве действия и противодействия выразится в виде

Проецируя (б) на оси координат, получаем

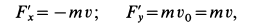
так как 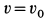. После этого

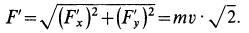
Направление силы давления жидкости 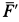указано на рисунке.

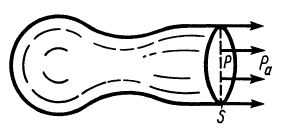
Рис. 43

Если бы через сечение 1 жидкость не поступала, а образовывалась внутри трубы, как в реактивном двигателе образуются газы после сгорания топлива, а через сечение 2 она выходила (рис. 43), то сила 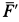, согласно (б), имела бы значение .

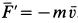Эта сила 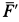является частью реактивной силы двигателя вследствие выброса продуктов сгорания из двигателя, являющегося источником газа. Другая часть реактивной силы двигателя, равная 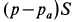, получается за счет разности давлений 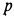, в струе выходящего из сопла газа и давления в среде 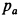, куда выходит из двигателя газ. Здесь 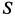— площадь выходного сечения сопла.

Полная реактивная сила двигателя

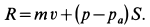
По направлению реактивная сила 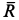всегда противоположна скорости v выходящего из двигателя газа. Для получения большой скорости выходящего газа сопло двигателя следует расширять по направлению к выходному его сечению при сверхзвуковых скоростях истечения газа.

• Заказать решение задач по теоретической механике

Теорема о движении центра масс системы

Следствием теоремы об изменении количества движения системы является теорема о движении центра масс системы. По теореме об изменении количества движения системы (13),

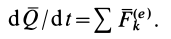
Но количество движения системы можно вычислить по формуле (6):

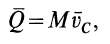
где 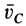— скорость центра масс; 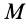— масса системы.

Подставляя (6) в (13) и учитывая, что масса системы постоянна, получаем теорему о движении центра масс в векторной форме:

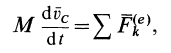
или

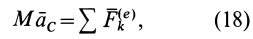
где 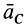— ускорение центра масс.  

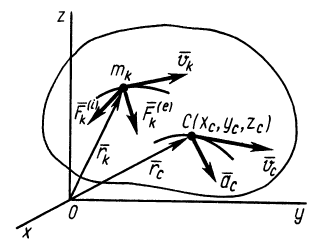
Рис. 44

Теорема о движении центра масс формулируется так: центр масс системы движется так же, как и материальная точка, масса которой равна массе всей системы, если на точку действуют все внешние силы, приложенные к рассматриваемой механической системе.

Проецируя (18) на прямоугольные декартовы оси координат (рис. 44), получаем дифференциальные уравнения движения центра масс:

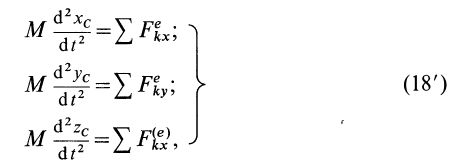
где 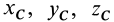— координаты центра масс.

Из теоремы о движении центра масс можно получить следствия, аналогичные законам сохранения количества движения и проекции количества движения на ось.

1.    Если главный вектор внешних сил, действующих на систему, равен нулю, т. е. 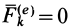, то из (18) следует, что ускорение центра масс 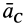равно нулю, а следовательно, скорость центра масс 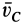является постоянной по модулю и направлению, т. е. центр масс движется прямолинейно и равномерно по инерции или находится в покое. Если, в частности, в начальный момент он находится в покое, то он покоится в течение всего времени, пока главный вектор внешних сил равен нулю.

2.    Если проекция, например на ось 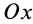, главного вектора внешних сил, действующих на систему, равна нулю, т. е.

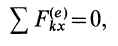
то из (18') следует, что проекция ускорения 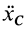центра масс на эту ось равна нулю, а следовательно, проекция скорости центра масс является постоянной величиной, т. е. .

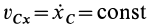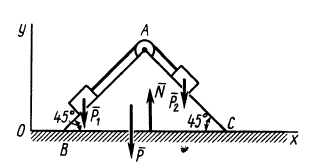
Рис. 45

Если дополнительно в начальный момент 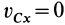, то тогда 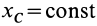, т. е. координата 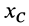центра масс не изменяется при движетении системы.

Внутренние силы не влияют явно на движение центра масс. Они могут влиять только неявно, через внешние силы. Следовательно, одними внутренними силами, без внешних, нельзя вывести из равновесия или изменить движение центра масс системы. Но внутренними силами для неизолированной механической системы можно создать движение отдельных частей системы и, следовательно, взаимодействие с внешними телами, вызывая этим внешние силы реакций связей или изменяя активные силы. Это может изменить движение центра масс или вывести его из равновесия.

Пусть человек стоит на абсолютно гладкой горизонтальной плоскости вблизи скрепленного с этой плоскостью тела. Так как на человека не действуют внешние силы в горизонтальном направлении, то внутренними силами он не может вывести из равновесия в этом направлении свой центр масс. Но человек может оттолкнуться рукой от препятствия, т. е. внутренними силами вызвать внешнюю силу реакций препятствия и таким образом вызвать движение своего центра масс в горизонтальном направлении. Все, что движется по Земле, летает в воздухе, плавает по воде, совершает это с помощью внутренних сил, создавая внешние силы трения на твердых поверхностях внешних тел, отталкиваясь от воздуха или воды.

Пример №2

Два груза с силами тяжест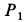и и 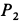, соединенные нерастяжимой нитью, переброшенной через блок, скользят по боковым граням равнобедренного клина (рис. 45). Клин стороной 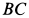опирается на гладкую горизонтальную плоскость. В начальный момент система находится в покое.

Найти перемещение клина по плоскости при опускании груза 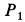на высоту 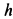. Сила тяжести клина  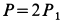и 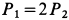. Массой блока и нити пренебречь.

Решение:

Внешними силами, действующими на клин вместе с грузами, являются силы тяжести 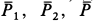и нормальная реакция горизонтальной гладкой поверхности 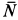. Следовательно,

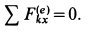
Учитывая, что в начальный момент система находится в покое, на основании второго следствия из теоремы о движении центра масс имеем .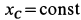

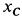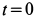Вычислим при  и 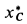 в момент, когда груз опустится на высоту .

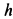Для момента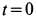

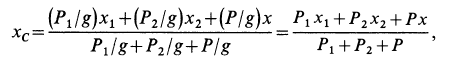
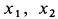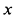где и — соответственно координаты центра масс по оси 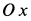грузов  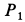и 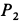и клина.

Пусть вся система вместе с клином переместилась в положительном направлении оси 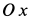на величину 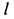при опускании груз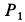а на 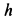. Тогда

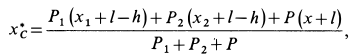
так как грузы вместе с клином передвинутся на 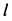вправо и по клину вдоль отрицательного направления оси 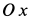на 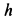при заданном угле клина, равном .

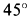Так как 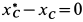, то после вычитания получим

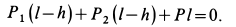
Отсюда

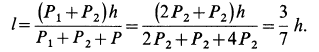
Так как величина 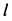оказалась положительной, то клин действительно перемещается вправо в положительном направлении оси .

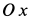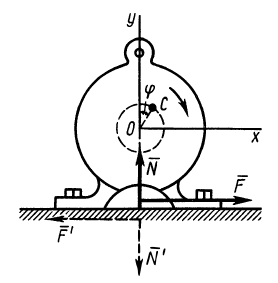
Рис. 46

Пример №3

В электромоторе корпус (статор) имеет силу тяжести 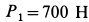, а ротор 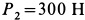. Ротор вращается по часовой стрелке с частотой 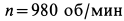(рис.46). Центр масс ротора вследствие его несимметричности отстоит от оси вращения на расстоянии .

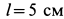Определить горизонтальную силу, с которой действует мотор на болты, крепящие его к фундаменту, и вертикальное давление на пол.

Решение:

Предположим, что при 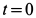центр масс ротора находится на оси 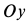. Тогда в момент времени 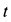координаты центра масс ротора можно выразить как

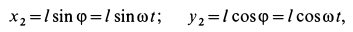
где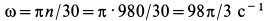 

Для определения давления мотора на болты и пол рассмотрим в качестве механической системы весь мотор, для которого внешней силой в горизонтальном направлении является только сила действия болтов 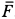, а в вертикальном направлении — силы тяжести и нормальная реакция пола 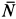. Для координат центра масс всего мотора

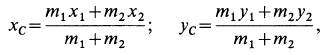
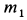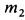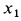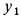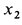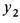где и — массы корпуса мотора и ротора соответственно; ,  и , — координаты их центров масс.

Центр масс корпуса закрепленного мотора является неподвижной точкой и находится в начале координат. Следовательно, 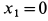,,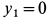 и поэтому координаты центра масс всего мотора

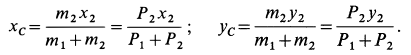
Используя дифференциальные уравнения движения центра масс всего мотора в проекциях на координатные оси, получим

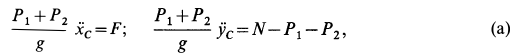
где 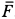—сила действия болтов на корпус мотора в горизонтальном направлении по оси 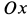; 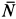—нормальная сила реакции пола. Так как

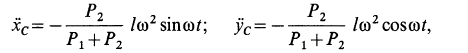
то из (а) следует

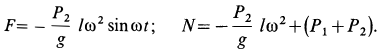
Сила действия мотора на болты 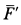 и давление 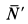на пол равны

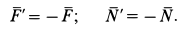
Наибольшие числовые значения этих сил

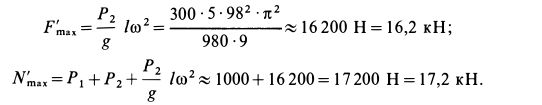
Если болтов нет, то корпус мотора может подпрыгивать в направлении оси 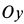. Динамическое условие подпрыгивания в рассматриваемом случае выразится как 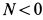, кинематическое условие подпрыгивания мотора есть .

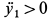Дифференциальные уравнения поступательного движения твердого тела

Из теоремы о движении центра масс системы получаются дифференциальные уравнения поступательного движения твердого тела. Имеем

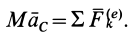
Но при поступательном движении твердого тела ускорения всех точек тела одинаковы по модулю и направлению, т. 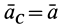е. , где 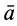—ускорение произвольной точки тела. Учитывая это, из теоремы о движении центра масс получаем следующее дифференциальное уравнение поступательного движения тела в векторной форме:

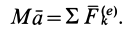
Проецируя на оси координат, имеем:

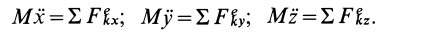
Это и есть дифференциальные уравнения поступательного движения твердого тела в проекциях на прямоугольные оси координат. В этих уравнениях х, у, z являются координатами произвольной точки тела, в частности могут быть координатами его центра масс. Тело, совершающее поступательное движение, имеет три степени свободы, и поэтому можно составить три дифференциальных уравнения его движения.

Дифференциальные уравнения поступательного движения твердого тела аналогичны дифференциальным уравнениям движения одной материальной точки. С помощью этих уравнений можно решать такие же задачи, как и для одной точки.