Теорема об изменении токов в электрической цепи при изменении сопротивления в одной ветви

Теорема об изменении токов в электрической цепи при изменении сопротивления в одной ветви:

На основании методов наложения и теоремы компенсации вытекает следующая теорема об изменении токов в электрической цепи, вызываемом изменением параметра в одной ветви данной цепи.

Если комплексное сопротивление какой-либо ветви электрической цепи изменится на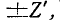

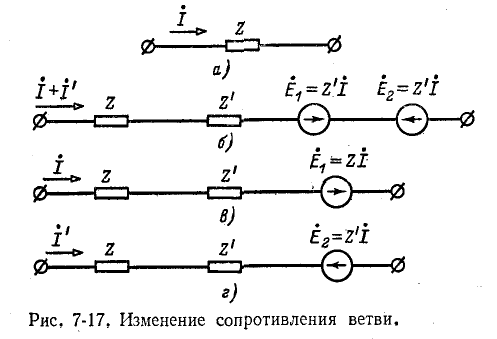
Сказанное поясняется на рис. 7-17.

Положим, что в ветви, комплексное сопротивление которой равно Z, проходит ток 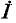(рис. 7-17, а). Спрашивается, как изменится ток, если сопротивление ветви изменится на 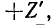т. е. станет равным Z + Z'.

На рис. 7-17, б показана ветвь с измененным сопротивлением; предполагается, что в результате изменения сопротивления Z на Z' первоначальный ток 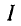изменился на 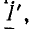т. е. стал равным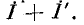

Включим в данную ветвь две противоположно направленные э. д. с. 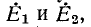равные 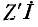каждая (ток в цепи при этом не изменится), и, пользуясь методом наложения, рассмотрим действие этих э. д. с. поочередно. При отсутствии 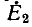получаются условия, тождественные первоначальным, так как схемы рис. 7-17,  эквивалентны: падение напряжения от тока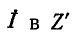компенсируется на основании теоремы компенсации дополнительной э. д. с. 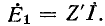Следовательно, изменение тока в цепи обусловливается действием э. д. с. с  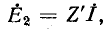направленной навстречу 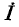(рис. 7-17, г), что и требовалось доказать.

Применение данной теоремы бывает целесообразным в тех случаях, когда известны токи в цепи до изменения параметров ветви.

Кроме того, измерив ток в электрической цепи с помощью амперметра, сопротивление которого известно, можно, основываясь на этой теореме, уточнить значение тока в цепи, т. е. исключить погрешность, вызванную сопротивлением прибора. Дополнительный ток, обусловленный сопротивлением прибора, согласно теореме равен:

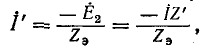
где 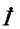— истинный ток (без амперметра); Z' — сопротивление амперметра; 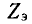— эквивалентное сопротивление пассивной цепи (с амперметром).

Через амперметр проходит ток

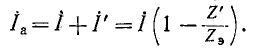
Следовательно, имея показание амперметра 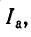можно вычислить искомый ток по формуле

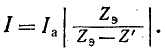
Следует заметить, что размыкание какой-либо ветви заданной электрической цепи соответствует предельному случаю 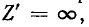, когда решение по приведенной выше теореме становится неопределенным. В этом случае применим любой из следующих приемов:

1. Включим между разомкнутыми точками два источника тока 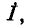соединенных параллельно. При принятом на рис. 7-18, а направлении этих источников ток в данной ветви в соответствии с первым законом Кирхгофа равен нулю. Применяя метод наложения и считая, что ток 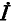выбран равным току в ветви до ее размыкания, приходим к выводу, что размыкание ветви равносильно добавлению к токам предшествующего режима новой системы токов, обусловленных действием в данной ветви пассивной электрической цепи источника тока, равного току, .протекавшему в той же ветви перед ее размыканием.
2. Обозначим через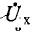напряжение между разомкнутыми выводами электрической цепи (напряжение холостого хода) и присоединим к ним источник э. д. с. 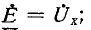токи и напряжения в цепи при этом не изменятся. Применив метод наложения, получим, что распределение токов и напряжений в исходной цепи слагается из соответствующих электрических величин двух схем (рис. 7-18, б): активной цепи с замкнутыми выводами и пассивной цепи с источником э. д. с. 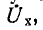присоединенным к указанным выводам.

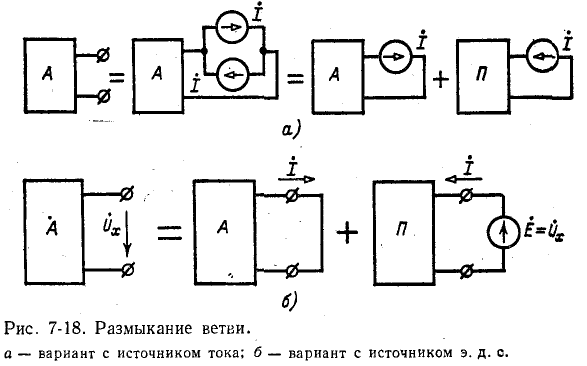
На рис. 7-18 буквой А обозначена заданная цепь, содержащая источники электрической энергии (активная цепь), а буквой П — та же цепь в предположении, что на месте источников оставлены только комплексные сопротивления или проводимости (пассивная цепь). Знаки сложения и равенства на рис. 7-18 относятся к токораспределениям.

Практическое применение теоремы об изменении токов в электрической цепи проиллюстрировано ниже на примере расчета несбалансированной мостовой схемы.

Пример 7-7.

Найти ток в диагональной ветви мостовой схемы рис. 7-19, а, если сопротивления в трех плечах моста равны 10 Ом каждое и сопротивление в четвертом плече равно 10,1 Ом; сопротивление диагональной ветви 1 Ом.

При равенстве сопротивлений всех плеч (10 Ом) ток в диагональной ветви отсутствовал бы и через каждое плечо проходил бы ток, равный 10/20= 0,5 А. Увеличение сопротивления одного плеча на 0,1 Ом равносильно на основании указанной выше теоремы введению в измененное плечо дополнительной э. д.с. 0,1 -0,5= 0,05 В (рис. 7-19,6). Последняя вызывает в диагональной ветви ток, который может быть вычислен по теореме об эквивалентном источнике э.д.с. . Искомый ток равен 0,00225 А.

Для вычисления этого тока можно также воспользоваться теоремой обратимости (вариант с э. д. с.), согласно которой искомый

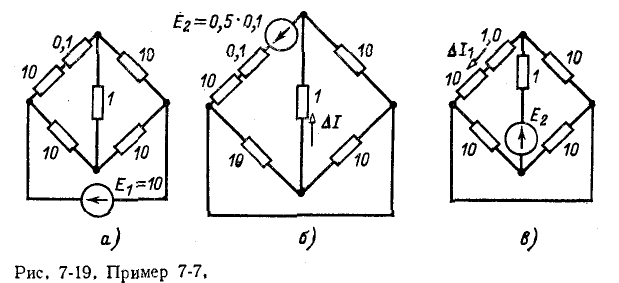
ток равен тому току, который проходил бы через плечо с сопротивлением 10,1 Ом, если бы источник э. Д. с. 0,05 В был перенесен в диагональную ветвь (рис. 7-19, в).

В этом случае расчет может быть упрощен, если пренебречь разницей в сопротивлениях плеч мостовой схемы; приближенное значение искомого тока получается равным 0,05/2,11 = 0,00227 А,