Теорема об изменении кинетической энергии в теоретической механике

Содержание:

Теорема об изменении кинетической энергии:

Для рассмотрения теоремы об изменении кинетической энергии необходимо ввести новое понятие «работа силы» и рассмотреть некоторые простейшие способы ее вычисления.

Работа силы

Работа силы на каком-либо перемещении является одной из основных характеристик, оценивающих действие силы на этом перемещении. Рассмотрим элементарную работу, полную работу и мощность.

Элементарная работа силы

Элементарная работа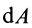

где 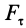— проекция силы  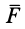на направление скорости точки приложения силы или на направление элементарного перемещения, которое считается направленным по скорости точки.

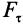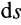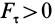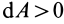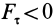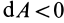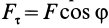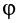Элементарная работа является скалярной величиной. Ее знак определяется знаком проекции силы , так как перемещение принимаем положительным. При элементарная работа , а при , наоборот, . Так как , где — угол между силой 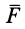и направлением скорости точки  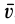, то  выражение (40) можно представить в виде

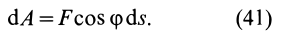
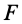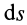В этой формуле величины и положительны и знак 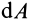определяется знаком 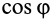. Если 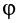— острый угол, то 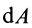положительна; если 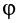тупой угол, то  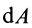отрицательна.

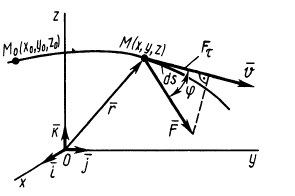
Рис. 60

Итак, элементарная работа силы равна произведению элементарного перемещения на проекцию силы на это перемещение. Отметим частные случаи, которые можно получить из (41):

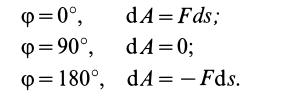
Таким образом, если сила перпендикулярна элементарному перемещению, то ее элементарная работа равна нулю. В частности, работа нормальной составляющей к скорости силы 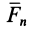всегда равна нулю.

Приведем другие формулы для вычисления элементарной работы силы. Из кинематики точки известно, что 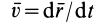; 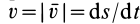. Следовательно, .

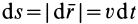После этого, согласно (41), элементарная работа

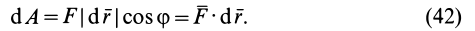
Элементарная работа силы равна скалярному произведению силы на дифференциал радиуса-вектора точки приложения силы.

Так как 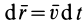, то, согласно (42),

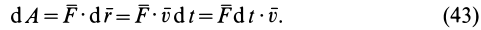
Элементарная работа равна скалярному произведению элементарного импульса силы на скорость точки.

Если силу 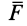 и радиус-вектор 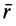разложить по осям координат, то

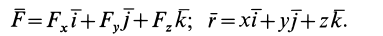
Из последней формулы имеем

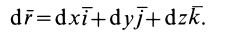
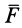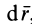Подставляя в (42) значения и , получаем

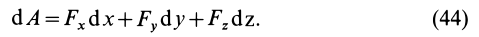
Формулу (44) называют обычно аналитическим выражением элементарной работы. Хотя выражение для элементарной работы (44) по форме и напоминает полный дифференциал функции координат точки, в действительности в общем случае элементарная работа не является полным дифференциалом. Элементарная работа является полным дифференциалом функции координат точки только для специального класса сил — так называемых стационарных потенциальных сил, которые рассмотрены ниже.

Полная работа силы

Для определения полной работы силы 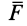на перемещении от точки 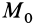до точки 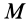разобьем это перемещение на 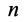перемещений, каждое из которых в пределе переходит в элементарное. Тогда работу 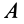можно выразить формулой

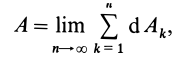
где 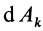— работа на 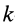-м элементарном перемещении, на которые разбито полное перемещение.

Так как сумма в определении работы является интегральной суммой определения криволинейного интеграла на участке кривой 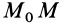, то, используя для элементарной работы формулу (40), получаем

Используя другие выражения для элементарной работы, полную работу силы можно представить также в виде

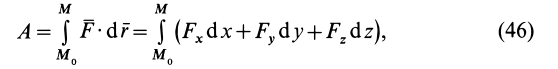
где момент времени 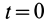соответствует точке 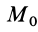, а момент времени 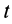— точке .

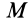Формула (47) особенно удобная для вычисления работы силы, когда сила известна как функция времени. Отметим, что из определения элементарной и полной работы следует:

1. работа равнодействующей силы на каком-либо перемещении равна алгебраической сумме работ составляющих сил на том же перемещении;
2. работа силы на полном перемещении равна сумме работ этой же силы на составляющих перемещениях, на которые любым образом разбито все перемещение.

Первое свойство, очевидно, достаточно доказать только для элементарной работы равнодействующей силы.

Если сила 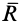является равнодействующей силой системы сил 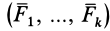, приложенных к рассматриваемой точке, то она выражается геометрической суммой этих сил. Тогда по определению элементарной работы силы имеем

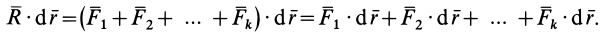
Первое свойство доказано.

Второе из отмеченных свойств непосредственно следует из возможности разбиения любым образом полного промежутка интегрирования на составляющие, причем определенный интеграл по полному промежутку интегрирования равен сумме интегралов по составляющим. Единицей полной работы, так же как и элементарной, в СИ является джоуль: .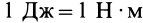

Если проекция силы на направление скорости 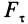является величиной постоянной, то из (45) получим

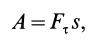
где 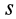—путь, пройденный точкой.

Так как 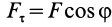, то последнюю формулу можно представить в виде

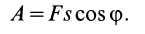
Следует отметить, что в этой формуле как 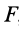, так и 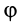могут быть переменными, но 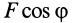является постоянной величиной. Это выполняется, есл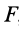и и 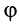постоянны. Если дополнительно угол 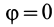или 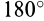, то тогда

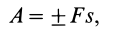
причем эта формула применима как для прямолинейного, так и для криволинейного движения. Для этого необходимо, чтобы сила 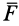была постоянной по модулю и все время направленной по касательной к траектории точки. В случае прямолинейной траектории сила 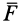, следовательно, должна быть все время направлена по траектории в одну и ту же сторону.

Мощность

Мощность силы или работоспособность какого-либо источника силы часто оценивают той работой, которую он может совершить за единицу времени.

Итак, по определению, мощность

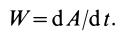
Учитывая (43) для элементарной работы, мощность можно представить в виде

Таким образом, мощность равна скалярному произведению силы на скорость точки. Из формулы (48) получаем, что чем больше скорость, тем меньше сила при одной и той же мощности. Следовательно, если от источника силы с заданной мощностью нужно получить большую силу, то ее можно получить только при малой скорости. Так, например, когда железнодорожному локомотиву надо увеличить силу тяги, то для этого надо уменьшить скорость поезда.

В СИ единицей мощности является ватт: .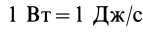

Примеры вычисления работы силы

Работа силы в общем случае зависит от характера движения точки приложения силы. Следовательно, для вычисления работы надо знать движение этой точки. Но в природе имеются силы и примеры движения, для которых работу можно вычислить сравнительно просто, зная начальное и конечное положение точки.

Рассмотрим работу силы тяжести и линейной силы упругости, изменяющейся по закону Гука, и вычисление работы силы, приложенной к какой-либо точке твердого тела в различных случаях его движения. В качестве простейших примеров движения укажем случаи, когда работа равна нулю. Так, работа любой силы равна нулю, если она приложена все время в неподвижной точке или в точках, скорость которых равна нулю, как, например, в случае, когда сила все время приложена в мгновенном центре скоростей при плоском движении тела или все время в точках, лежащих на мгновенной оси вращения, в случае вращения тела вокруг неподвижной точки. Эти случаи возможны в задачах, когда рассматривают работу силы трения в точке соприкосновения двух тел при отсутствии скольжения одного тела по другому. При этом работа силы трения равна нулю.

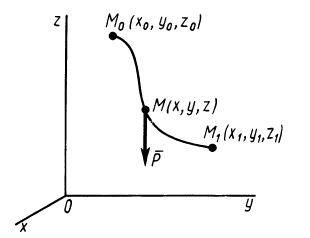
Рис. 61

Работа силы тяжести

Силу тяжести 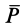материальной точки массой 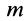вблизи поверхности Земли можно считать постоянной, равной 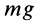, направленной по вертикали вниз. Если взять оси координат 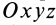, у которых ось  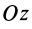направлена по вертикали вверх (рис. 61), то

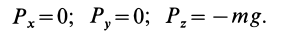
Вычисляя работу 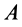силы 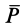на перемещении от точки 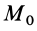до точки 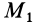по формуле (46), имеем

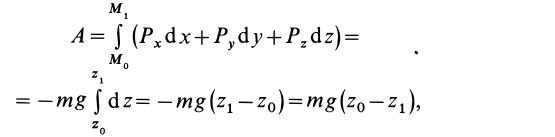
или

где 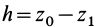 — высота опускания точки.

При подъеме точки высота 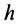является отрицательной. Следовательно, в общем случае работа силы тяжести 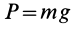равна

Работа силы тяжести равна произведению этой силы на высоту опускания (работа положительна) или высоту подъема (работа отрицательна). Из формулы (50) следует, что работа силы тяжести не зависит от формы траектории между точкам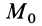и и 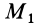, и если эти точки совпадают, то работа силы тяжести равна нулю (случай замкнутого пути). Она равна нулю, если точк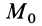и и 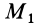лежат в одной и той же горизонтальной плоскости.

Рис. 62

Если имеем систему 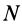материальных точек, то для каждой точки с массой 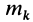будем иметь работу ее силы тяжести

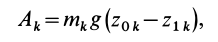
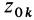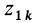где и — начальная и конечная координаты точки.

Работа всех сил тяжести системы материальных точек

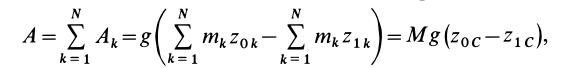
так как

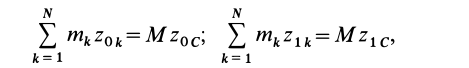
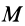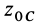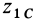где — масса системы точек; и — начальная и конечная координаты центра масс системы точек. Вводя обозначение для изменения высоты центра масс 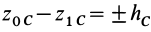, имеем

Из (50') следует, что для перемещений точек системы, при которых 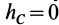, работа сил тяжести .

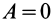Работа линейной силы упругости

Линейной силой упругости (или линейной восстанавливающей силой) называют силу, действующую по закону Гука (рис. 62):

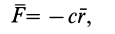
где 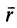— расстояние от точки равновесия, где сила равна нулю, до рассматриваемой точки 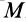; 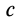—постоянный коэффициент жесткости.

Выберем начало координат в точке равновесия 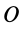, тогда

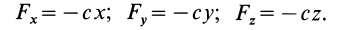
После этого работу на перемещении от точки 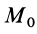до точки  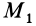определим по формуле

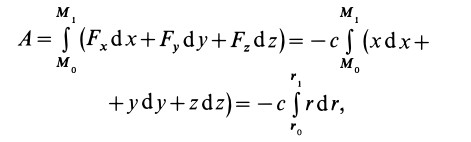
так как

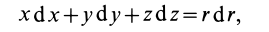
где .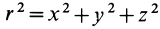

Выполняя интегрирование, получаем

По этой формуле вычисляют работу линейной силы упругости пружины при перемещении по любому пути из точки 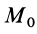, в которой ее удлинение (начальная деформация) равно 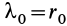, в точку 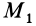, где деформация соответственно равна 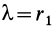. В новых обозначениях (51) принимает вид

При перемещении из положения равновесия (пружина не деформирована), где 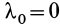, в любое положение с деформацией 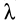работа линейной силы упругости

Работа линейной силы упругости на перемещении из состояния равновесия всегда отрицательна и равна половине произведения коэффициента жесткости на квадрат деформации. Из формулы (51) или (52) следует, что работа линейной силы упругости не зависит от формы перемещения и работа по любому замкнутому перемещению равна нулю. Она также равна нулю, если точк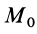и  и 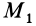лежат на одной сфере, описанной из точки равновесия.

Работа силы, приложенной к твердому телу

Получим формулы для вычисления элементарной и полной работы силы, приложенной в какой-либо точке твердого тела, которое совершает то или иное движение. Сначала рассмотрим поступательное и вращательное движения тела, а затем общий случай движения твердого тела.

При поступательном движении твердого тела все точки тела имеют одинаковые по модулю и направлению скорости (рис. 63). Следовательно, если сила 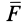приложена к точке 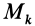, то, так как ,

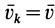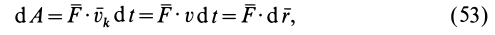
где 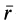—радиус-вектор произвольной точки твердого тела.

На каком-либо перемещении полная работа

При вращении твердого тела вокруг неподвижной оси скорость точки 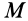можно вычислить по векторной формуле Эйлера (рис. 64):

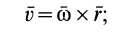
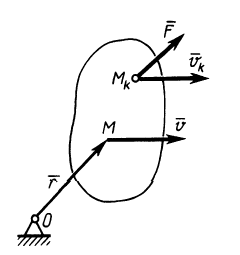
Рис. 63    

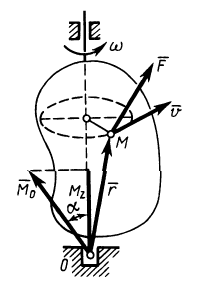
Рис. 64

тогда элементарную работу силы 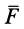определим по формуле

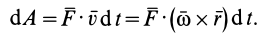
В смешанном векторном произведении, которое выражается в виде определителя, можно переставлять сомножители в круговом порядке:

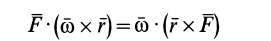
и

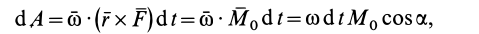
так как

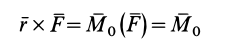
является моментом силы относительно точки .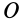

Учитывая, что 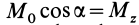— момент силы относительно оси вращения 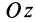и 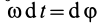, окончательно получаем

Таким образом, элементарная работа силы, приложенной к какой-либо точке тела, вращающегося вокруг неподвижной оси, равна произведению момента силы относительно оси вращения на дифференциал угла поворота тела.

Полная работа

В частном случае, если момент силы относительно оси вращения является постоянным, т. е. 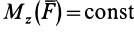, работу определяют по формуле

где 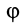— угол поворота тела, на котором вычисляют работу силы.

Так как 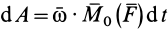, то мощность в случае вращения твердого тела вокруг неподвижной оси

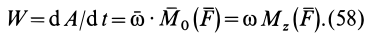
Мощность силы, приложенной к вращающемуся вокруг неподвижной оси твердому телу, равна произведению угловой скорости тела на момент силы относительно оси вращения . тела.

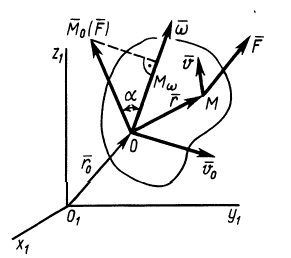
Рис. 65

Для свободного тела в общем случае движения скорость точки 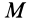, в которой приложена сила 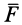(рис. 65),

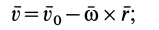
следовательно,

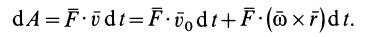
Учитывая, что

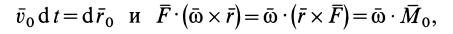
имеем

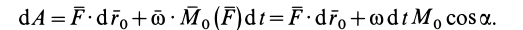
Но так как 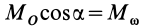— момент силы относительно мгновенной оси относительного вращения вокруг точки 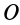, 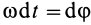— элементарный угол поворота вокруг этой оси, то окончательно получаем

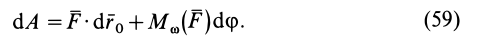
Таким образом, элементарная работа силы, приложенной в какой-либо точке твердого тела, в общем случае движения складывается из элементарной работы на элементарном поступательном перемещении вместе с какой-либо точкой тела и на элементарном вращательном перемещении вокруг этой точки.

В случае вращения твердого тела вокруг неподвижной точки, выбрав эту точку за полюс 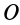, по (59) для элементарной работы имеем

Поворот на угол 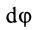следует рассматривать в каждый момент времени вокруг своей мгновенной оси вращения.

Формулу (59) применяют и для плоского движения твердого тела, только в этом случае мгновенная ось относительного вращения перпендикулярна плоскости движения и проходит через произвольную точку тела.

При действии на твердое тело системы сил 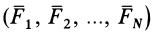 для элементарной работы силы 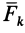, согласно полученным формулам, имеем

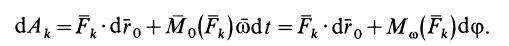
Элементарная работа системы сил

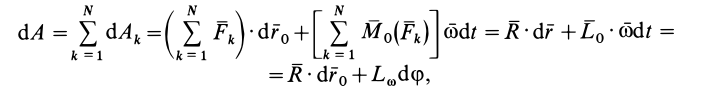
где

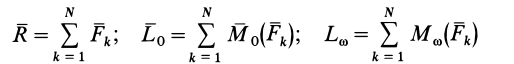
соответственно являются главным вектором и главными моментами системы сил относительно точки 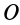и мгновенной оси относительного вращения, проходящей через точку полюс. Таким образом,

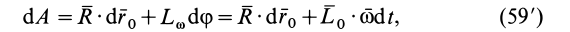
т. е. элементарная работа системы сил, приложенных к свободному твердому телу в общем случае его движения, складывается из элементарной работы главного вектора системы сил на элементарном поступательном перемещении вместе с какой-либо точкой тела и элементарной работы главного момента этих сил относительно выбранной точки на элементарном вращательном перемещении вокруг этой точки.

Работа внутренних сил твердого тела

Докажем, что для твердого тела сумма работ внутренних сил равна нулю при любом его перемещении. Очевидно, достаточно доказать, что сумма элементарных работ всех внутренних сил равна нулю. Рассмотрим две любые точки твердого тела: 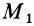и 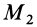(рис. 66). Так как внутренние силы есть силы взаимодействия точек тела, то для этих двух точек

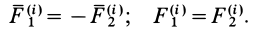
Введем единичный вектор 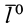, направленный по силе 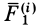. Тогда

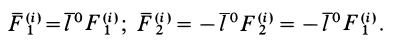
Сумма элементарных работ сил 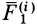и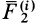 

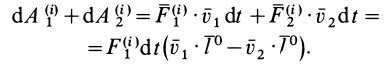
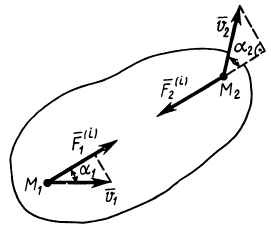
Рис. 66

Раскрывая скалярные произведения векторов в скобках, получаем

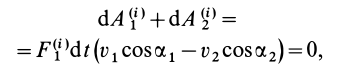
так как в кинематике твердого тела доказано, что проекции скоростей любых двух точек твердого тела на направление прямой линии, соединяющей эти точки, равны друг другу при любом движении твердого тела. В полученном выражении в скобках стоит разность этих проекций скоростей двух точек, т. е. величина, равная нулю.

Твердое тело можно считать состоящим из пар взаимодействующих точек, для каждой из которых сумма элементарных работ внутренних сил равна нулю.

Суммируя элементарные работы для всех пар точек, получаем .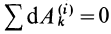

Как уже известно, главный вектор и главный момент всех внутренних сил для любой механической системы равны нулю. Сумма работ внутренних сил равна нулю только в случае твердого тела, а для любой механической системы в общем случае она не равна нулю.

В задачах в качестве механической системы часто рассматривают систему сочлененных твердых тел. При вычислении работы всех сил, приложенных к такой системе тел, очевидно, достаточно учесть работу внутренних сил в местах сочленения твердых тел. Если твердые тела сочленяются с помощью шарниров без трения, сумма работ таких двух внутренних сил равна нулю, так как внутренние силы в точке сочленения, как действие и противодействие, равны по модулю, но противоположны по направлению, а перемещение у точек приложения сил общее.

Таким образом, сочленение твердых тел с помощью шарниров без трения при вычислении работы внутренних сил не нарушает жесткости системы тел, так как сумма работ внутренних сил в этих шарнирах равна нулю при любых перемещениях системы сочлененных твердых тел. Систему сочлененных с помощью таких шарниров твердых тел при вычислении работы всех внутренних сил можно считать одним твердым телом. Это характерно и для случая сочленения системы твердых тел с помощью нерастяжимых нитей, канатов и т. п. В этом случае работа внутренних сил натяжений также равна нулю.

Кинетическая энергия

Кинетическая энергия точки и системы: Кинетической энергией материальной точки называют половину произведения массы точки на квадрат ее скорости, т.е. 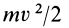или 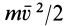, так как скалярный квадрат любого вектора равен квадрату модуля этого вектора. Кинетическая энергия является скалярной положительной величиной. В СИ единицей кинетической энергии является джоуль: .

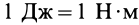Кинетической энергией системы 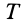называют сумму кинетических энергий всех точек механической системы, т. е.

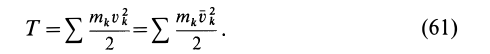
Кинетическая энергия как точки, так и системы не зависит от направления скоростей точек. Кинетическая энергия может быть равна нулю для системы только при условии, если все точки системы находятся в покое.

Вычисление кинетической энергии системы (теорема Кёнига)

Разложим движение механической системы на переносное поступательное вместе с центром масс системы и относительное по отношению к системе координат, движущейся поступательно вместе с центром масс. Аналогично тому, как это производилось при выводе формулы для кинетического момента при таком разложении абсолютного движения, для каждой точки системы (см. рис. 57) имеем

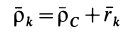
и соответственно

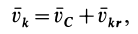
где 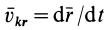является относительной скоростью точки, так как подвижная система координат движется поступательно 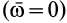и, следовательно, полная производная по времени от 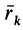совпадает с локальной производной, равной относительной скорости точки.

Подставляя значение скорости 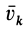в выражение кинетической энергии абсолютного движения системы, т. е. ее движения относительно системы координат 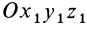, после очевидных преобразований получаем

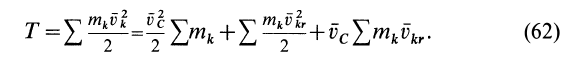
Но

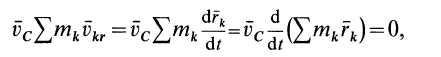
так как

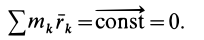
Учитывая, что 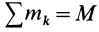 —масса системы, и обозначая  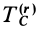второе слагаемое в (62), имеем

где

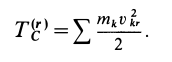
Величина 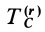 является кинетической энергией относительного движения системы относительно системы координат, движущейся поступательно вместе с ее центром масс, или кинетической энергией системы относительно центра масс.

Формула (63) выражает так называемую теорему Кёнига: кинетическая энергия системы в абсолютном движении складывается из кинетической энергии центра масс, если в нем сосредоточить всю массу системы, и кинетической энергии системы относительно центра масс.

Кинетическая энергия твердого тела

При поступательном движении твердого тела кинетическая энергия

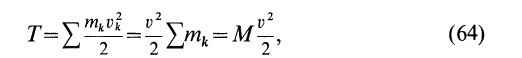
так как при поступательном движении твердого тела скорости всех точек тела одинаковы, т. 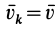е. , где 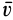— общая скорость для всех точек тела.

Таким образом, кинетическая энергия твердого тела при поступательном движении вычисляется так же, как и для одной точки, у которой масса равна массе всего тела.

При вращении тела вокруг неподвижной оси кинетическую энергию можно вычислить, если учесть, что скорость какой-либо точки тела 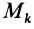можно выразить (см. рис. 50) как

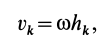
где 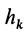 — кратчайшее расстояние от точки 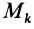до оси вращения; 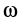— угловая скорость тела.

Тогда

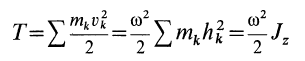
или

где 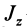— момент инерции тела относительно оси вращения .

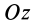Следовательно, кинетическая энергия тела при вращательном движении вокруг неподвижной оси равна половине произведения момента инерции тела относительно оси вращения на квадрат угловой скорости тела.

Из сравнения (64) и (65) следует, что эти формулы подобны, только при вращательном движении аналогом массы является момент инерции тела относительно оси вращения, а скорости— угловая скорость тела. Такая аналогия между поступательным и вращательным движениями твердого тела может наблюдаться во многих формулах, относящихся к этим двум движениям.

При плоском движении твердого тела кинетическую энергию можно вычислить по теореме Кёнига. Так как в этом случае относительное движение относительно центра масс (точнее, относительно системы координат, движущейся поступательно вместе с центром масс) является вращением вокруг центра масс с угловой скоростью 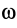, то

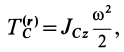
где 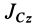— момент инерции тела относительно оси 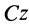, проходящей через центр масс тела перпендикулярно плоскости движения. Следовательно, на основании (63) для плоского движения тела имеем

Таким образом, при плоском движении тела кинетическая энергия складывается из кинетической энергии поступательного движения тела вместе с центром масс и кинетической энергии от вращения вокруг оси, проходящей через центр масс и перпендикулярной плоскости движения.

Учитывая, что 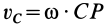 ( 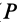— мгновенный центр скоростей), из (66), используя теорему Штейнера, получаем еще одну формулу для кинетической энергии твердого тела при плоском движении:

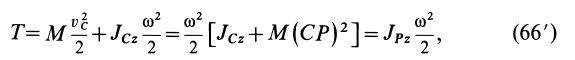
где 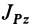— момент инерции тела относительно оси 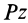, проходящей через мгновенный центр скоростей перпендикулярно плоскости движения,

Если механическая система состоит из нескольких твердых тел, то следует вычислить кинетическую энергию каждого тела, а затем полученные кинетические энергии сложить. Так определяется кинетическая энергия системы тел.

Теорема об изменении кинетической энергии точки

Для материальной точки массой 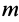, движущейся под действием силы 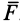, основной закон динамики можно представить в виде

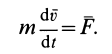
Умножая обе части этого соотношения скалярно на дифференциал радиуса-вектора точки 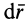, имеем

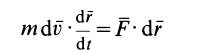
или

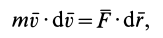
где 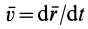— скорость точки.

Учитывая, что 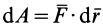— элементарная работа, получаем

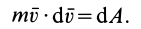
Так как

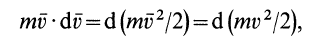
то окончательно

Формула (67) выражает теорему об изменении кинетической энергии для точки в дифференциальной форме: дифференциал кинетической энергии точки равен элементарной работе силы, действующей на точку.

Если обе части (67) разделить на 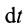и учесть, что 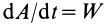—мощность, то теорему можно также выразить в виде

Производная по времени от кинетической энергии точки равна мощности, подводимой к этой точке.

Интегрируя обе части (67) от точки 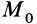до точки 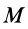(см. рис. 60), получаем теорему об изменении кинетической энергии точки в конечной форме:

т. е. изменение кинетической энергии точки на каком-либо перемещении равно работе силы, действующей на точку на том же перемещении.

• Заказать решение задач по теоретической механике

Пример 1. Тело, имеющее силу тяжести 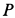, падает без начальной скорости на пружину с высоты 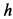. Определить наибольшее обжатие пружины 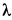, если статическое сжатие ее под действием силы тяжести этого тела равно 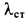. Массой пружины пренебречь (рис. 67).

Решение. Применим к движению тела теорему об изменении кинетической энергии точки

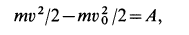
приняв за начальное положение тела начало его падения с высоты 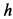, а за конечное — момент максимального обжатия пружины. Изменение кинетической энергии за этот промежуток времени равно нулю, так как 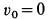и при наибольшем сжатии пружины 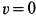. Следовательно, работа 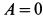. На тело после его соприкосновения с пружиной действуют две силы: сила тяжести тела 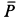и сила упругости пружины. Сила 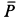совершает работу на перемещении 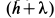, сила упругости — на перемещении 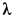. Следовательно,

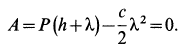
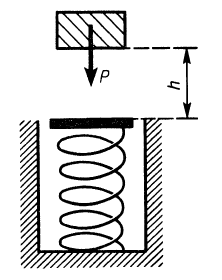
Рис. 67

Но так как в положении статического равновесия 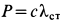, то 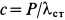. Поэтому  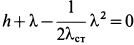или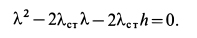

Решая это квадратное уравнение, имеем

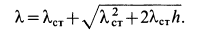
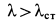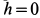Знак плюс перед корнем выбран потому, что . При наибольшее обжатие пружины 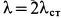, т. е. при динамическом действии груза на пружину ее наибольшее обжатие в два раза больше статического обжатия.

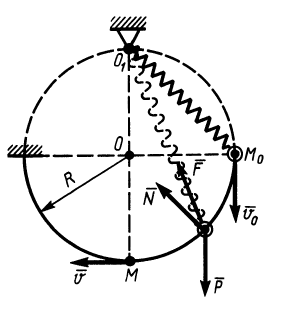
Рис. 68

Пример 2. Грузу с силой тяжести 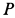, подвешенному в точке  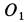на пружине, статическое удлинение которой под действием силы тяжести 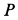равно 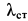, сообщена начальная скорость 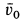из положения 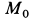вертикально вниз (рис. 68).

Определить скорость груза в положении 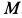, если груз, принимаемый за точку, скользит по кольцу радиусом 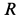без трения, 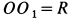и естественная длина пружины равна .

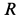Решение. Применим к движению груза теорему об изменении кинетической энергии, приняв за начальное положение груза 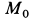и конечное — 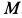. Получим

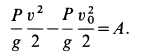
Работу совершают сила тяжести груза и сила упругости пружины. Нормальная реакция кольца 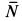все время перпендикулярна перемещению, и ее работа равна нулю. Следовательно,

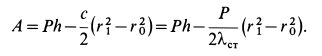
В рассматриваемом случае

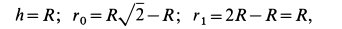
поэтому

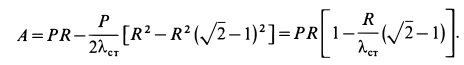
По теореме об изменении кинетической энергии имеем

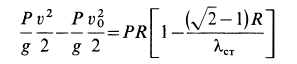
и

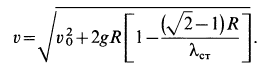
Теорема об изменении кинетической энергии системы

Приложив к точкам системы все внешние и внутренние силы, для каждой точки системы можно выразить теорему об изменении кинетической энергии (67) в форме

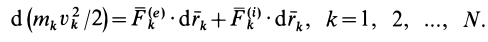
Суммируя правые и левые части этих соотношений по всем точкам системы и вынося знак дифференциала за знак суммы, получаем

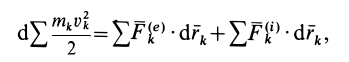
или

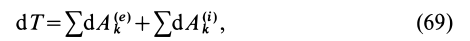
где кинетическая энергия системы

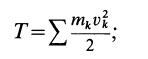
элементарная работа внешних и внутренних сил соответственно будет

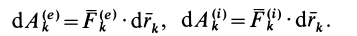
Формула (69) и выражает теорему об изменении кинетической энергии системы в дифференциальной форме: дифференциал от кинетической энергии системы равен сумме элементарных работ всех внешних и внутренних сил, действующих на систему.

Если обе части (69) проинтегрировать между двумя положениями системы — начальным и конечным, в которых соответственно кинетическая энергия 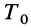и 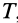, то, изменяя порядок суммирования и интегрирования, имеем

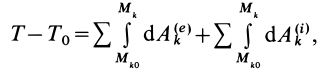
или

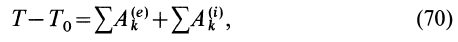
где 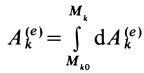 —работа внешней силы для точки системы  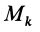при ее перемещении из начального положения 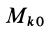в конечное положение 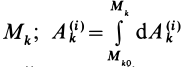— соответственно работа внутренней силы, действующей на точку .

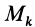Формула (70) выражает теорему об изменении кинетической энергии системы в конечной или интегральной форме: изменение кинетической энергии системы при ее перемещении из одного положения в другое равно сумме работ всех внешних и внутренних сил, действующих на систему, на соответствующих перемещениях точек системы при том же перемещении системы.

Частный случай: Для абсолютно твердого тела сумма работ всех внутренних сил системы равна нулю:

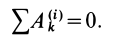
Следовательно, теорему об изменении кинетической энергии, например, в конечной форме можно представить в виде

Изменение кинетической энергии твердого тела при каком-либо перемещении равно сумме работ всех внешних сил, действующих на тело, на соответствующих перемещениях точек тела при том же перемещении твердого тела.

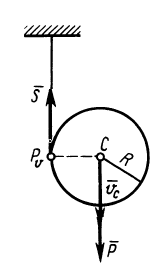
Рис. 69

Таким образом, в отличие от рассмотренных других общих теорем динамики системы в теорему об изменении кинетической энергии могут входить внутренние силы. Они не входят в эту теорему в случае абсолютно твердого тела.

Пример 1. В маятнике Максвелла однородный цилиндр силой тяжести 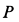и радиусом 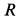падает вниз без начальной скорости, разматывая нить, намотанную на цилиндр в его среднем сечении.

Определить скорость оси цилиндра в зависимости от высоты ее опускания 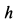(рис. 69).

Решение. По теореме об изменении кинетической энергии цилиндра как твердого тела имеем

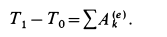
Так как в начальный момент времени цилиндр покоится, то 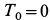. Цилиндр совершает плоское движение. Его кинетическая энергия в момент достижения высоты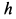 

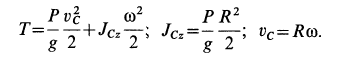
Поэтому

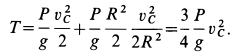
Внешними силами являются сила тяжести 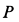и сила натяжения нити 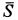. Сила  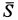все время приложена в мгновенном центре скоростей цилиндра, имеющем скорость равную нулю. Работа силы тоже равна нулю. Следовательно,

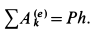
Подставляя вычисленные величины в теорему об изменении кинетической энергии, получаем

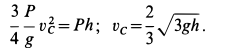
Пример 2. Груз 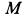, имеющий силу тяжести 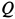, с помощью нити, переброшенной через блок 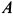, приводит в движение каток 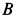, катящийся без скольжения по горизонтальной плоскости (рис. 70). Блок 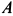и каток 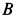— однородные диски радиусом 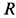. Их силы тяжести равны 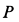. Коэффициент трения качения катка 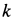. Трением в осях катка и блока, а также массой нити пренебречь.

Определить скорость груза 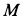в зависимости от его высоты опускания.

В начальный момент система покоится.

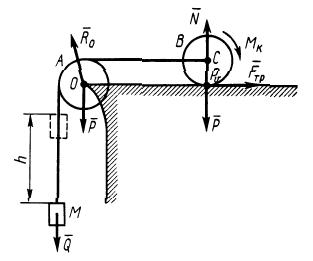
Рис. 70    

Решение. По теореме об изменении кинетической энергии системы, состоящей из груза, нити, блока и катка, имеем

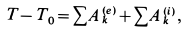
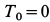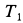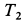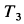где , так как вначале система покоилась. Обозначив ,  и  кинетические энергии груза, блока и катка соответственно после опускания груза на высоту 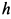, получаем

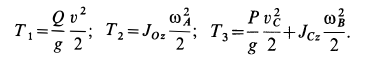
Но

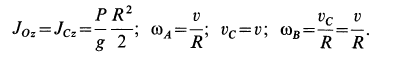
Следовательно,

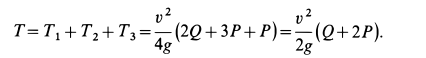
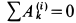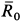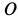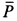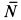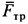Так как работа внутренних сил натяжений нити равна нулю, то вообще  для всей системы твердых тел, соединенных нитью. Работа сил тяжести блока и реакции оси  равны нулю, так как эти силы приложены в неподвижной точке . Сила тяжести катка перпендикулярна перемещению, а силы и приложены в мгновенном центре скоростей и, следовательно, работа их равна нулю. Работу производят сила 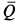и пара сил с моментом 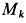, препятствующим качению катка по плоскости. Имеем

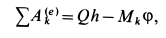
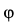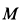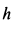где — угол поворота катка при опускании груза на и .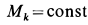

Так как

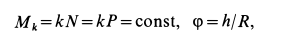
то

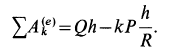
Подставляя значения полученных величин в теорему об изменении кинетической энергии, получаем

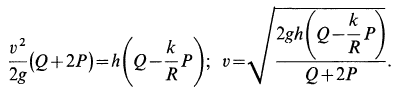
Заметим, что груз имеет не только силу тяжести 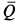, совершающую работу, но он еще обладает массой 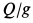и, следовательно, имеет кинетическую энергию. И работа силы тяжести, и кинетическая энергия груза входят в теорему об изменении кинетической энергии.

Теорема об изменении кинетической энергии в относительном движении

Теорема об изменении кинетической энергии материальной точки. Пусть точка 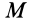совершает переносное движение вместе с подвижной системой координат 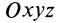относительно основной системы координат 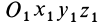и относительное движение по отношению к системе координат 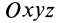(рис. 71). Абсолютным движением точки 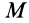является ее сложное движение относительно системы координат 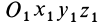. Дифференциальное уравнение относительного движения точки 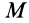в векторной форме можно представить в виде

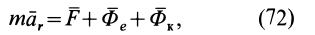
где 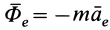— сила инерции переносного движения точки;  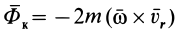 — сила инерции Кориолиса.

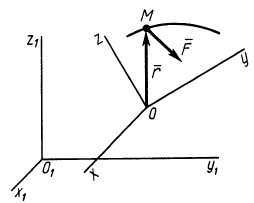
Рис. 71    

Вывод теоремы об изменении кинетической энергии для точки в относительном движении произведем так же, как и вывод аналогичной теоремы в абсолютном движении, умножив обе части (72) скалярно на вектор элементарного относительного перемещения 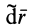, и преобразуем левую часть полученного выражения. Значок 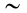над дифференциалом радиуса-вектора 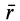и других векторов указывает, что при дифференцировании надо брать изменение соответствующего вектора относительно подвижной системы координат 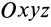. Таким образом,

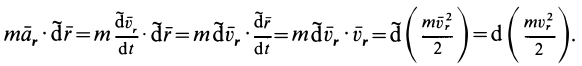
В правую часть входят элементарные работы сил 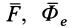 и 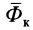на относительном перемещении 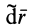. Оказывается, что элементарная работа силы инерции Кориолиса на относительном элементарном перемещении всегда равна нулю, так как эта сила перпендикулярна относительной скорости 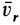и, следовательно, перпендикулярна относительному перемещению 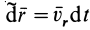. В выражение силы инерции Кориолиса входит векторное произведение 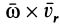, а оно всегда перпендикулярно каждому из векторов сомножителей, в частности .

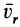Итак, теорема об изменении кинетической энергии точки в дифференциальной форме имеет вид

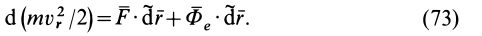
Теорема об изменении кинетической энергии в относительном движении точки выражается так же, как и в абсолютном движении, только к элементарной работе приложенной силы добавляют элементарную работу силы инерции переносного движения на относительном перемещении.

Теорема об изменении кинетической энергии системы

Для системы рассмотрим наиболее важный случай, когда в качестве переносного движения берется поступательное движение системы вместе с центром масс и, следовательно, кинетическую энергию системы в абсолютном движении можно вычислить на основании теоремы Кёнига (63): .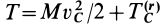

Теорему об изменении кинетической энергии системы для абсолютного движения (см. рис. 56) можно представить в виде

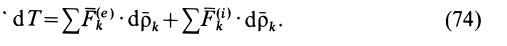
Так как

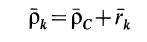
и, следовательно,

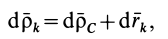
то, заменяя в (74) 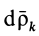и 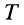их значениями, получаем

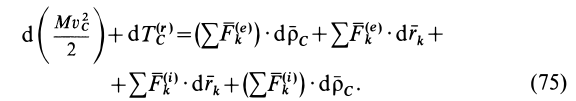
По свойству внутренних сил, .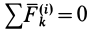

Если теорему об изменении кинетической энергии для центра масс выразить так же, как и для точки, у которой масса равна массе всей системы, и эта точка находится под действием всех внешних сил, действующих на систему, то

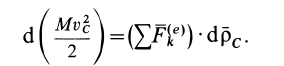
Отбросив в (75) эти члены, получим следующую теорему об изменении кинетической энергии системы в относительном движении по отношению к системе координат, движущейся поступательно вместе с центром масс:

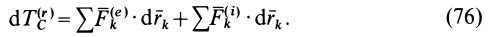
Сравнивая (76) с (74), видим, что теорема об изменении кинетической энергии в относительном движении системы по отношению к системе координат, движущейся поступательно вместе с центром масс системы, формулируется так же, как и для абсолютного движения системы.