Теорема об изменении кинетического момента в теоретической механике

Содержание:

Кинетический момент точки и системы:

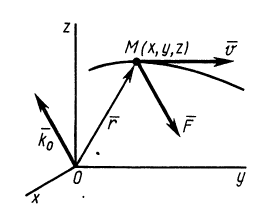
Рис. 47

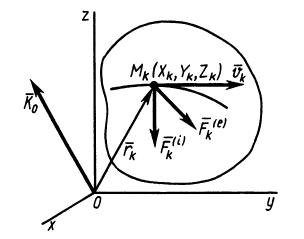
Рис. 48

Наряду с количеством движения в качестве векторной меры движения можно использовать кинетический момент, или момент количества движения. Для материальной точки массой 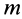, движущейся со скоростью 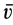, кинетическим моментом 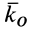относительно какого-либо центра 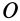(рис. 47), т. е.

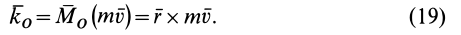
Кинетический момент 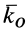приложен к точке 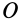, относительно которой он вычисляется.

Проецируя обе части (19) на прямоугольные декартовы оси, получаем кинетические моменты точки относительно этих осей координат, если точка 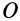является началом осей координат:

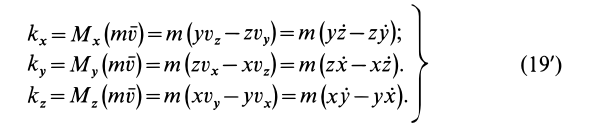
В физике кинетический момент точки иногда называют моментом импульса точки.

Единица кинетического момента в СИ — 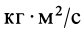, или .

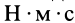Для механической системы кинетическим моментом 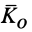(или главным моментом количества движения системы относительно какой-либо точки 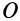) называют векторную сумму кинетических моментов точек этой системы, взятых относительно точки 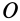(рис. 48), т. е.

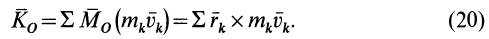
Кинетический момент системы 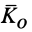приложен к точке 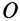, относительно которой он вычисляется.

Если спроецировать (20) на прямоугольные декартовы оси координат, то получим проекции кинетического момента на эти оси, или кинетические моменты относительно осей координат:

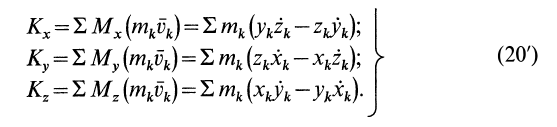
Кинетический момент относительно оси вращения при вращательном движении твердого тела

Вычислим кинетический момент твердого тела относительно оси вращения, когда тело вращается вокруг этой неподвижной оси с угловой скоростью 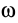(рис. 49). По определению кинетического момента относительно оси [(см. формулы (20')] имеем

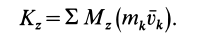
Но при вращении тела вокруг оси 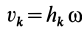, причем количество движения точки  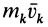перпендикулярно отрезку 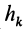и лежит в плоскости, перпендикулярной оси вращения 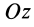. Следовательно, момент количества движения относительно оси 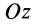для одной точки

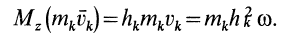
Для всего тела

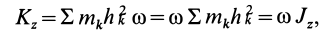
т. е.

Таким образом, кинетический момент тела относительно оси вращения при вращательном движении равен произведению угловой скорости тела на его момент инерции относительно оси вращения. Знак кинетического момента относительно оси совпадает со знаком угловой скорости вращения вокруг этой оси: при вращении против часовой стрелки кинетический момент положительный; при вращении по часовой стрелке — отрицательный.

Дополнительно без вывода приведем формулы для кинетических моментов относительно двух других осей координат 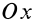 и 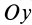, перпендикулярных оси вращения 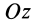. Имеем

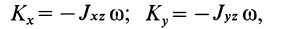
где 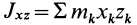и 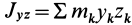— центробежные моменты инерции.

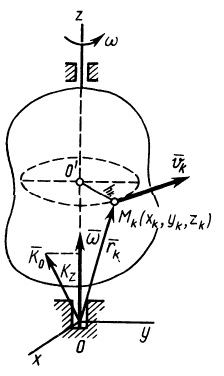
Рис. 49

Эти формулы можно получить как частный случай более общих формул для случая вращения твердого тела вокруг неподвижной точки. Они могут быть получены и непосредственно.

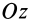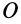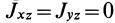Если ось вращения является главной осью инерции для точки , то  и, следовательно  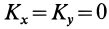для этой точки. В этом случае кинетический момент 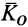относительно точки 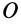направлен по оси вращения. В общем случае 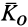не направлен по оси вращения, так как имеет не равные нулю проекци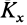и и 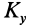 на оси координат, перпендикулярные оси вращения .

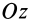Теорема об изменении кинетического момента точки

Для материальной точки основной закон динамики можно представить в виде

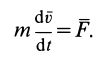
Умножая обе части этого соотношения слева векторно на радиус-вектор 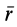(см. рис. 48), получаем

В правой части этой формулы имеем момент силы относительно неподвижной точки 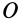. Преобразуем левую часть, применив формулу производной от векторного произведения:

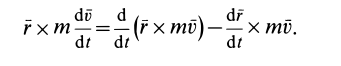
Но

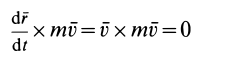
как векторное произведение параллельных векторов.

После этого из (22) получаем

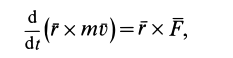
или

Таким образом, первая производная по времени от кинетического момента точки относительно какого-либо центра равна моменту силы относительно того же центра.

Это и есть теорема об изменении кинетического момента для точки.

Проецируя (23) на прямоугольные декартовы оси координат, получаем теоремы об изменении кинетического момента точки относительно этих осей координат:

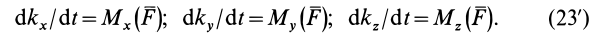
Теорема об изменении кинетического момента системы

Если к точкам системы приложить все внешние и внутренние силы (рис. 48), то для каждой точки системы можно выразить теорему об изменении кинетического момента в форме (23), т. е.

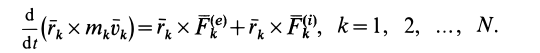
Суммируя правые и левые части этих соотношений по всем точкам системы и заменяя суммы производных производной от суммы, получаем

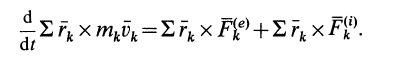
Так как, по свойству внутренних сил,

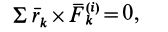
а по определению кинетического момента системы,

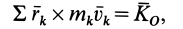
то

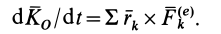
Если обозначить главный момент всех внешних сил 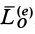,  т. е.

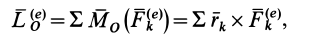
то теорему об изменении кинетического момента системы можно представить в виде

Следовательно, первая производная по времени от кинетического момента системы относительно какой-либо точки равна векторной сумме моментов внешних сил, действующих на систему, относительно той же точки.

В эту теорему входит кинетический момент системы 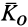в ее движении относительно инерциальной системы отсчета, причем кинетический момент и моменты внешних сил вычисляются относительно неподвижной в этой системе отсчета точки 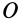. Получим теорему об изменении кинетического момента системы такого же движения, но выберем в качестве точки при вычислении кинетического момента и моментов внешних сил точку 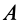, движущуюся относительно инерциальной системы отсчета со скоростью .

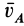По определению кинетического момента системы относительно точки 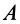имеем (рис. 50)

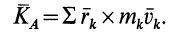
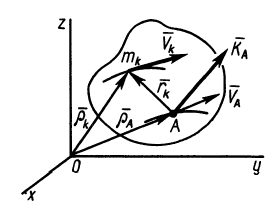
Рис. 50  

Вычислим производную по времени от кинетического момента 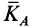по правилу дифференцирования векторных произведений. Получим

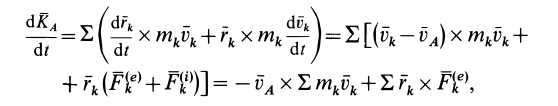
так как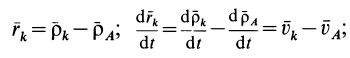

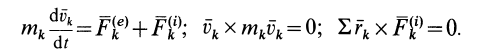
Учитывая, что 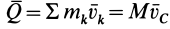, получим

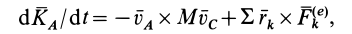
или

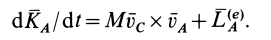
Рассмотрим частные случаи этой теоремы.

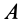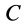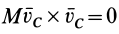1.    Если точка совпадает с центром масс , то  и теорема принимает форму

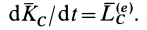
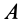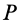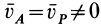2.    Если в случае плоского движения твердого тела выбрать в качестве точки мгновенный центр скоростей , то , так как в рассматриваемом случае 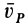есть скорость движения мгновенного центра скоростей по неподвижной центроиде, а она не равна нулю в отличие от скорости точки тела, совпадающей с точкой 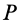, которая равна нулю. Очевидно, 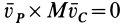, если 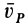параллельна 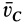, т.е. если касательные к центроидам и траектории центра масс параллельны или, что то же самое, центр масс находится на нормали к центроидам в точке 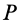. Тогда

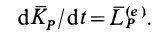
Эти частные случаи показывают, что для подвижных точек центра масс для любой системы и мгновенного центра скоростей при плоском движении твердого тела в рассмотренном случае теорема об изменении кинетического момента для абсолютного движения имеет ту же форму, что и для неподвижной точки .

Внутренние силы непосредственно не влияют на изменение кинетического момента системы. Они могут влиять на него только через внешние силы, т. е. неявно.

Проецируя (24) на прямоугольные декартовы оси координат, получаем теоремы об изменении кинетического момента системы относительно этих осей координат, т. е.

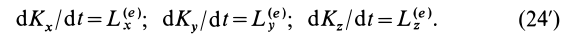
Теорема об изменении кинетического момента позволяет изучать вращательное движение твердого тела вокруг оси и точки или вращательную часть движения тела в общем случае движения свободного твердого тела.

Законы сохранения кинетических моментов

Выведем законы сохранения кинетических моментов для системы, рассматривая материальную точку как механическую систему, у которой число точек равно единице. Естественно, что для одной материальной точки все действующие на нее силы являются внешними. Возможны следующие частные случаи теоремы об изменении кинетического момента системы.

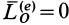1.    Если главный момент внешних сил системы относительно точки равен нулю, т. е. , то, согласно (24), кинетический момент системы 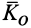относительно той же точки постоянен по модулю и направлению, т. е.

Этот частный случай теоремы об изменении кинетического момента системы называют законом сохранения кинетического момента. В проекциях на прямоугольные декартовы оси координат по этому закону

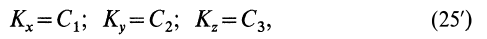
где 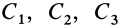 — постоянные величины.

Соотношения (25') являются первыми интегралами дифференциальных уравнений движения системы (3). Закон сохранения кинетического момента системы показывает, что одни внутренние силы не могут изменить кинетический момент системы, так же как они не изменяют ее количество движения.

2.    Если сумма моментов всех внешних сил системы относительно оси 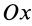 равна нулю, т. е. 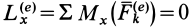, то из (24') следует, что

Следовательно, кинетический момент системы относительно какой-либо координатной оси постоянен, если сумма моментов внешних сил относительно этой оси равна нулю, что, в частности, наблюдается, когда внешние силы параллельны оси или пересекают ее. В частном случае для тела или системы тел, которые все вместе могут вращаться вокруг неподвижной оси, и если при этом

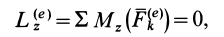
то

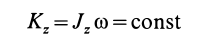
или

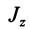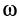где и  — момент инерции системы тел и их угловая скорость относительно оси вращения в произвольный момент времен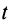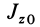и ; и 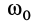— момент инерции тел и их угловая скорость в момент времени, выбранный за начальный, например при .

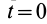Закон сохранения кинетического момента в форме (27) используют в своей деятельности акробаты, прыгуны, танцоры и т. д. Наглядно его можно продемонстрировать в опыте на скамье Жуковского (рис. 51). Если человек с гирями в руках встанет на горизонтальную платформу скамьи Жуковского, которая может вращаться вокруг вертикальной оси почти без трения, и затем ему сообщить угловую скорость вокруг этой оси, то

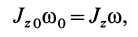
так как внешние силы или параллельны оси вращения (силы веса человека, гирь и платформы), или пересекают ось (реакции подшипника, если пренебречь силами трения).

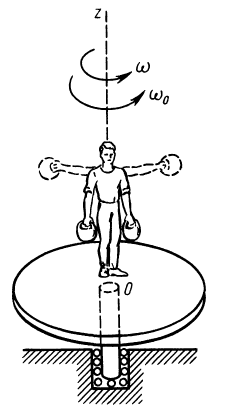
Рис. 51

Следовательно, если человек увеличит момент инерции, например разведением рук с гирями в сторону, то угловая скорость вращения уменьшится, и наоборот. В действительности угловая скорость хотя и медленно, но все время уменьшается вследствие наличия сопротивления воздуха и трения в подшипнике скамьи.

Пример:

Однородный горизонтальный диск радиусом 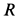и силой тяжести 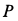может вращаться без трения вокруг вертикальной оси. Как изменится угловая скорость диска, если первоначально стоящий на диске на расстоянии 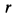от его оси человек с силой тяжести  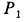пойдет по окружности радиусом 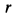по диску с относительной скоростью 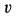(рис. 52)?

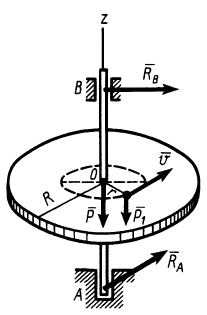
Рис. 52

Решение:

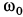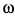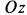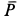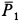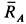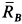Пусть угловая скорость диска вначале была , а потом вследствие движения человека по диску стала . Так как внешние силы для системы, состоящей из человека и диска, параллельны оси  (силы тяжести и ) или ее пересекают (реакции   и ), то

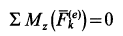
и, следовательно,

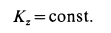
Составим 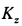для двух моментов времени и приравняем друг другу. В начальный момент, когда человек стоит, кинетический момент системы определяется как

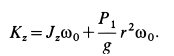
После того как человек пойдет по диску, его кинетический момент станет равным кинетическому моменту от вращения вместе с диском плюс кинетический момент от относительного движения по диску, если человек идет в сторону вращения диска, т. е.

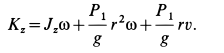
Приравнивая полученные выражения кинетических моментов, получаем

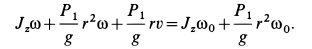
Отсюда

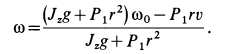
Для однородного диска

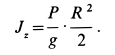
Поэтому угловая скорость

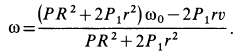
Угловая скорость диска от движения по нему человека уменьшилась на 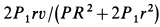. Если вместо диска рассматривать земной шар, то движение по нему материальных объектов (воздуха, течения воды и т. д.), которые имеют не равную нулю проекцию скорости на касательную к параллелям, вызовет изменение угловой скорости вращения Земли. Она уменьшится, если проекции скорости положительны для направления по вращению земного шара, и увеличится, если против вращения.

Дифференциальное уравнение вращения твердого тела вокруг неподвижной оси

Из теоремы об изменении кинетического момента (24') получим дифференциальное уравнение вращения твердого тела вокруг неподвижной оси 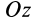(рис. 53). Имеем

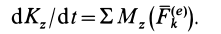
Для случая вращения твердого тела вокруг неподвижной оси, согласно (21), имеем

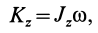
где 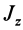— постоянный для твердого тела момент инерции относительно неподвижной оси вращения; 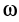— угловая скорость. Учитывая это, получаем

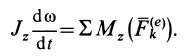
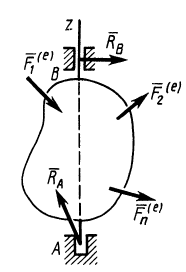
Рис. 53

Если ввести угол поворота тела 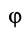, учитывая, что 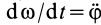, имеем

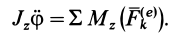
Это и есть дифференциальное уравнение вращения твердого тела вокруг неподвижной оси. Оно полностью аналогично дифференциальному уравнению поступательного движения твердого тела в проекции на какую-либо ось, например на ось .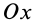

В дифференциальное уравнение вращения тела вокруг неподвижной оси вместо координаты 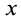входит угол поворота 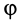, вместо массы тела 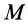—момент инерции относительно оси вращения 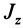, вместо суммы проекций внешних сил на ось  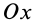— сумма моментов внешних сил относительно оси вращения 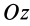или так называемый вращательный момент внешних сил.

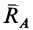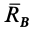Реакции подшипников и оси вращения являются внешними силами, но их моменты относительно оси вращения равны нулю, так как они пересекают ось, если пренебречь силами трения.

В частном случае, когда

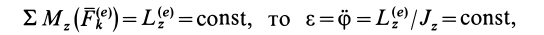
т. е. вращение тела происходит с постоянным угловым ускорением.

Если

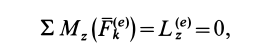
то

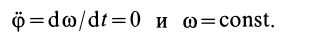
Это случай равномерного вращения тела по инерции без действия вращательного момента внешних сил.

Дифференциальное уравнение вращательного движения твердого тела в общем случае позволяет решать две основные задачи: по заданному вращению тела определять вращающий момент внешних сил и по заданному вращательному моменту и начальным условиям находить вращение тела. При решении второй задачи для нахождения угла поворота как функции времени приходится интегрировать дифференциальное уравнение вращательного движения. Методы его интегрирования полностью аналогичны рассмотренным выше методам интегрирования дифференциального уравнения прямолинейного движения точки.

Движение точки под действием центральной силы

Теорема площадей:

Наряду с введенными в кинематике точки скоростью 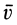и ускорением 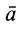можно ввести другие характеристики движения точки, например секторные скорость и ускорение. Секторной скоростью точк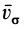и или 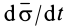 относительно точки 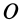(рис. 54) называют векторную величину, определяемую по формуле

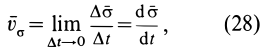
где 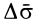 — вектор, численно равный заштрихованной на рисунке площади, ометаемой радиусом-вектором  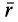движущейся точки за время 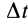; направление вектора 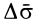берется по перпендикуляру к заштрихованной площади так, чтобы с конца этого вектора при ометании заштрихованной площади видеть поворот радиуса-вектора 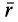против часовой стрелки.

Для случая движения точки по плоскости секторная скорость перпендикулярна этой плоскости, если точка 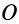выбрана в той же плоскости, в которой движется точка. Секторная скорость всегда приложена в той точке, относительно которой она вычисляется.

Секторное ускорение 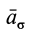 можно ввести как производную по времени от вектора секторной скорости, т. е.

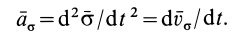
Секторную скорость можно выразить через момент линейной скорости 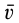относительно точки :

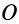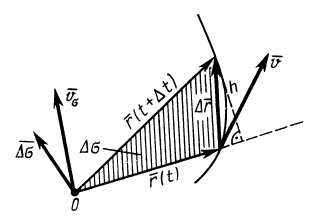
Рис. 54

Векторное произведение 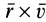, согласно определению, имеет такое же направление, как и 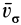. Следовательно, для доказательства формулы (29) достаточно показать, что величины левой и правой частей одинаковы. Вычислим левую часть формулы (29):

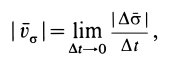
но

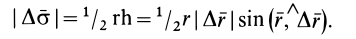
Следовательно,

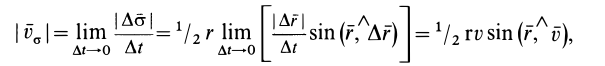
что совпадает с модулем векторного произведения, стоящим справа в формуле (29).

Если движение точки происходит в плоскости, то секторную скорость можно считать алгебраической величиной. В этом случае секторную скорость точки часто выражают в полярных координатах. Из формулы (29) секторная скорость

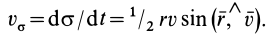
Но из кинематики точки в полярной системе координат на плоскости известно (рис. 55), что .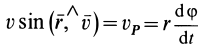

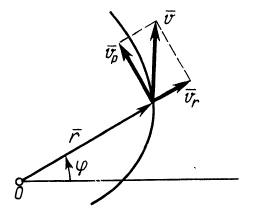
Рис. 55

Следовательно,

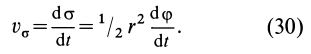
Формула (30) выражает секторную скорость в полярных координатах в случае плоского движения точки.

Используя формулу (29), кинетический момент через секторную скорость можно выразить в виде

Соответственно теорему об изменении кинетического момента (23) для точки можно выразить через секторную скорость формулой

В форме (32) теорему об изменении кинетического момента для точки называют теоремой площадей.

Движение точки под действием центральной силы

Центральной силой 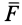 называют такую силу, линия действия которой при движении точки ее приложения проходит через одну и ту же точку 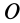, называемую центром центральной силы.

Центральная сила может быть притягивающей (направленной к центру) и отталкивающей (направленной от центра). Так как для центральной силы _момент силы относительно своего центра равен нулю, т. е. 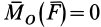, то, следовательно, по теореме об изменении кинетического момента для точки (23),

В проекциях на прямоугольные оси декартовой системы с началом в точке 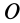по (33) имеем:

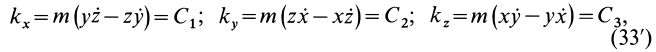
где 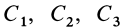— постоянные величины.

Умножая первое соотношение (33') на 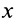, второе — на 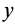, третье — на 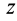и складывая, получаем 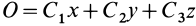, т.е. координаты движущейся точки 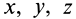удовлетворяют уравнению плоскости, проходящей через начало координат.

Следовательно, траектория точки, движущейся под действием центральной силы, является плоской кривой, лежащей в плоскости, проходящей через центр силы.

Так как при движении точки под действием центральной силы

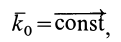
то, учитывая формулу (31), имеем

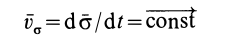
и, следовательно,

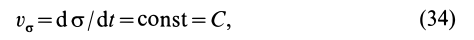
или

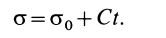
Формула (34) выражает так называемый интеграл площадей: при движении точки под действием центральной силы секторная скорость является постоянной величиной и, следовательно, ометаемая радиусом-вектором площадь пропорциональна времени.

Учитывая формулу (30), интеграл площадей (34) в полярных координатах можно представить в виде

В этой форме интеграл площадей широко используется при рассмотрении движения планет вокруг Солнца и вообще различных спутников, в частности искусственных спутников Земли.

Теорема об изменении кинетического момента системы в относительном движении по отношению к центру масс

Рассмотрим относительное движение системы только относительно системы координат, движущейся поступательно вместе с центром масс системы.

Прежде чем рассмотреть теорему, выведем формулу для вычисления кинетического момента системы.

Формула для кинетического момента системы

Пусть механическая система совершает движение относительно основной системы координат 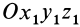. Возьмем подвижную систему координат 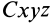с началом в центре масс системы 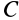, движущуюся поступательно относительно основной системы координат. Из рис. 56 следует, что для любого момента времени .

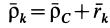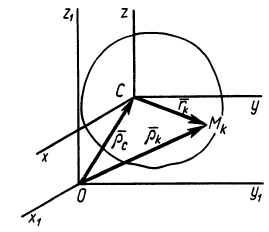
Рис. 56

Дифференцируя это тождество по времени, получаем

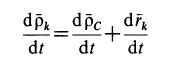
или

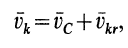
где 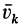— абсолютная скорость точки 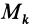, 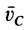— абсолютная скорость центра масс;  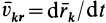— относительная скорость точки 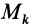относительно подвижной системы координат 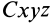. При поступательном движении подвижной системы координат ее угловая скорость 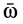равна нулю и по формуле Бура полная производная по времени от радиуса-вектора 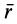совпадает с локальной производной, равной относительной скорости.

Согласно определению кинетического момента 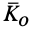относительно неподвижной точки 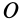, для абсолютного движения системы относительно системы координат 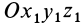по формуле (20) имеем

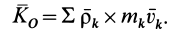
Подставляя в эту формулу значения 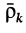 и 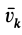, после небольших преобразований получаем

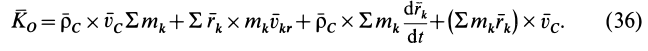
В этой формуле 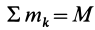— масса системы. Кроме того, последние два слагаемых равны нулю. Действительно, по определению радиуса-вектора центра масс относительно этого центра масс имеем

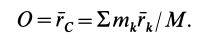
Следовательно, 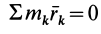и последнее слагаемое в (36) тоже равно нулю.

Другое слагаемое можно предварительно преобразовать:

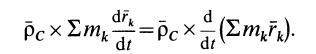
Это слагаемое также равно нулю, так как все время 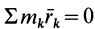. Формула (36) принимает следующий окончательный вид:

где .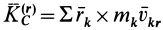

Величина 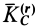является кинетическим моментом системы относительно центра масс для относительного движения относительно системы координат, движущейся поступательно вместе с центром масс, т. е. системы координат .

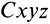Формула (37) показывает, что кинетический момент абсолютного движения системы относительно неподвижной точки 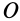 равен векторной сумме кинетического момента центра масс относительно той же точки, если бы в центре масс была сосредоточена вся масса системы, и кинетического момента системы относительно центра масс для относительного движения системы по отношению к подвижной системе координат, движущейся поступательно вместе с центром масс.

Теорема об изменении кинетического момента системы в относительном движении по отношению к центру масс. Для абсолютного движения системы и неподвижной точки 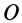теорема об изменении кинетического момента имеет вид

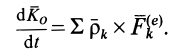
Подставляя сюда значения 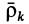и 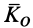по формуле (37) и производя дифференцирование и группировку членов, получаем

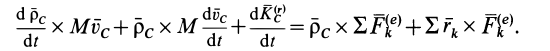
Перенося из правой части в левую первое слагаемое и учитывая, что

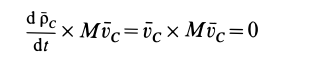
как векторное произведение параллельных векторов, после объединения слагаемых имеем

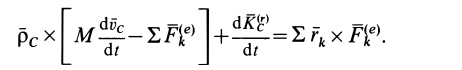
В этой формуле выражение в квадратных скобках равно нулю на основании теоремы о движении центра масс системы (18) и, следовательно, формула примет вид

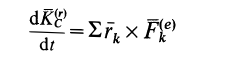
или

где 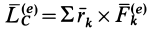 является главным моментом всех внешних сил относительно центра масс.

Формула (38) и выражает рассматриваемую теорему об изменении кинетического момента системы относительно центра масс для относительного движения системы по отношению к системе координат, движущейся поступательно с центром масс; она формулируется так же, как если бы центр масс был неподвижной точкой.

Эту теорему применяют для изучения вращательной части плоского движения и движения свободного твердого тела вокруг центра масс.

Дифференциальные уравнения плоского движения твердого тела

Используя теоремы о движении центра масс и изменении кинетического момента системы относительно центра масс для относительного движения системы по отношению к системе координат, движущейся поступательно с центром масс, получим дифференциальные уравнения плоского движения твердого тела.

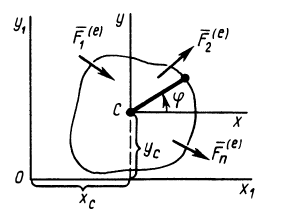
Рис. 57

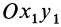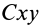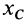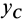В плоскости движения центра масс тела, совершающего плоское движение, выберем неподвижную систему координат , относительно которой рассматривается движение, и движущуюся поступательно вместе с центром масс систему (рис. 57).  Пусть и — координаты центра масс тела относительно неподвижной системы координат. Тогда по теореме о движении центра масс получим два следующих дифференциальных уравнения плоского движения твердого тела:

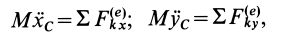
где 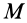— масса тела.

Третье дифференциальное уравнение плоского движения твердого тела получим из теоремы об изменении кинетического момента в относительном движении по отношению к центру масс (38) в проекции на подвижную ось :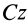

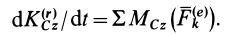
Плоское движение твердого тела можно считать состоящим из поступательного движения вместе с центром масс 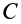и вращения вокруг подвижной оси 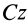. Для случая вращения вокруг оси кинетический момент относительно этой оси вычисляется по формуле

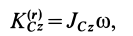
где 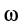— угловая скорость; 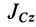— момент инерции тела относительно оси .

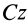Так как 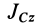является величиной постоянной, то после подстановки 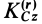в теорему об изменении' кинетического момента в относительном движении получим

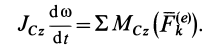
Если ввести угол поворота 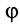 вокруг подвижной оси 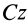, то получим следующее дифференциальное уравнение:

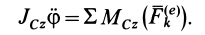
Таким образом, для твердого тела, совершающего плоское движение и, следовательно, имеющего три степени свободы, соответственно получим следующие три дифференциальных уравнения:

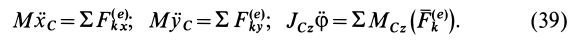
С помощью этих уравнений можно решать две основные задачи: по заданному плоскому движению твердого тела находить действующие на тело внешние силы и по заданным внешним силам и начальным условиям определять его движение. При решении этих задач должны быть заданы масса тела 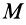и его момент инерции.

• Заказать решение задач по теоретической механике

Теорема Резаля

Теореме об изменении кинетического момента системы можно дать следующее кинематическое истолкование. Из кинематики точки известно, что скорость точки можно рассматривать как скорость конца радиуса-вектора, следящего за движущейся точкой, или как скорость изменения самого радиуса-вектора, если он проведен в движущуюся точку из какой-либо неподвижной точки (рис. 58). Траектория движущейся точки при этом является годографом радиуса-вектора г, а скорость точки направлена по касательной к этому годографу и равна первой производной по времени от радиуса-вектора. Аналогично этому, и производную по времени от кинетического момента можно рассматривать как своеобразную скорость конца этого вектора при движении по годографу кинетического момента (рис. 59). Эта скорость не является обычной скоростью точки, так как кинетический момент имеет иную размерность, чем радиус-вектор. Это есть скорость изменения вектора кинетического момента.

Таким образом, если обозначить через 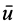скорость конца кинетического момента, т. е. 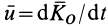, то теорему об изменении кинетического момента системы (24) можно представить в новой форме — в виде так называемой теоремы Резаля:

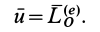
Теорему Резаля можно сформулировать так: при движении механический системы скорость точки, совпадающей с концом вектора кинетического момента при движении по годографу этого вектора, равна по величине и параллельна по направлению главному моменту всех внешних сил системы. Точка, относительно которой вычисляются кинетический момент системы и главный момент внешних сил, одна и та же.

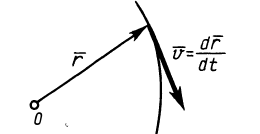
Рис. 58

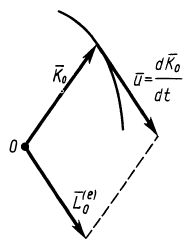
Рис. 59

В форме теоремы Резаля может быть сформулирована и теорема об изменении кинетического момента в относительном движении по отношению к центру масс.

Теорема Резаля особенно удобна для приближенного исследования движения быстровращающихся гироскопов.

Аналогично и теорему об изменении количества движения для системы можно сформулировать в форме теоремы Резаля для количества движения: при движении механической системы скорость точки, совпадающей с концом вектора количества движения при движении по его годографу, равна по величине и параллельна по направлению главному вектору всех внешних сил, действующих на систему.