Теорема об эквивалентном источнике

Теорема об эквивалентном источнике:

Теорема об эквивалентном источнике часто применяется в расчетах электрических цепей. С помощью этой важной теоремы сложная электрическая схема с произвольным числом источников электрической энергии приводится к схеме с одним источником, благодаря чему расчет электрической цепи упрощается.

Существуют два варианта теоремы об эквивалентном источнике: вариант с источником э. д. с. и вариант с Источником тока.

Теорема об эквивалентном источнике э. д. с.

Ток в любой ветви тп линейной электрической цепи не изменится, если электрическую цепь, к которой подключена данная ветвь, заменить эквивалентным источником э. д. с., которая должна быть равна напряжению на выводах разомкнутой цепи тп, а внутреннее сопротивление источника

должно равняться входному сопротивлению пассивной электрической цепи со стороны выводов т и п при разомкнутой ветви mn.

Данная теорема доказывается следующим образом: в ветвь тп вводятся две равные и противоположно направленные э. д. с.

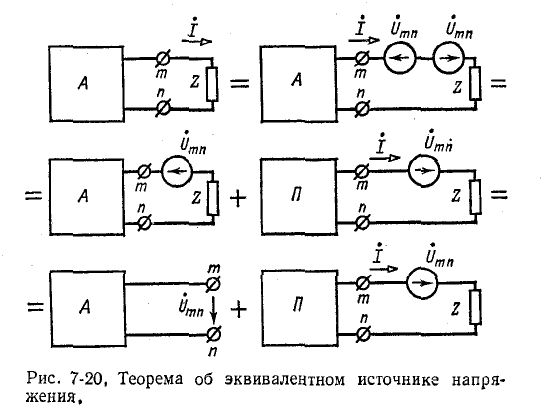
Применение метода наложения в соответствии с рис. 7-20 приводит к выводу, что ток в ветви Z равен:

где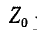— комплексное сопротивление всей пассивной цепи П. Таким образом, ток в ветви Z получается в предположении, что данная ветвь подключена к источнику э. д. с., которая равна 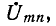а внутреннее сопротивление равно 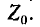Стедует заметить, что в соответствии с рис. 7-20 ток в какой-либо другой ветви заданной электрической цепи может быть получен в результате алгебраического сложения тока, проходящего через эту ветвь при разомкнутых выводах т и п, с током, возникающим в ней под воздействием э. д. с. 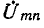в ветви Z (когда остальная цепь пассивна). Поэтому, если известно распределение токов в электрической цепи при разомкнутой ветви Z, то последующее распределение

токов при включенной ветви находится весьма легко наложением на предыдущий режим тех токов, которые обусловливаются воздействием на пассивную цепь э. д. с. 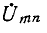в ветви Z.

Как уже указывалось выше, метод наложения применим. не только к токам, но и к напряжениям. Поэтому, пользуясь описанным приемом, можно находить также и распределение напряжений.

При наличии в электрической цепи нескольких источников э. д. с. и тока одинаковой частоты напряжение холостого хода является линейной функцией заданных э. д. с. и токов источников.

Для доказательства теоремы, об эквивалентном источнике в ветвь вводились две противоположно направленные

э.    д. с., равные напряжению холостого хода в этой ветви. Такой же прием может быть применен одновременно и к двум ветвям любой сложной активной цепи. Тогда действительное токораспределение в цепи получится как сумма токораспределений в двух схемах:

1. в активной схеме — при разомкнутых двух ветвях;
2. в пассивной схеме — при питании ее из двух ветвей источниками э. д. с., равными напряжениям холостого хода на этих ветвях и направленными по токам, т. е. так же, как напряжения холостого хода.

Указанный прием представляет удобство в том случае, когда известно токораспределенне при режиме холостого хода для обеих ветвей. Тогда при замыкании этих ветвей достаточно лишь наложить токи, полученные из второй схемы с двумя э. д. с.

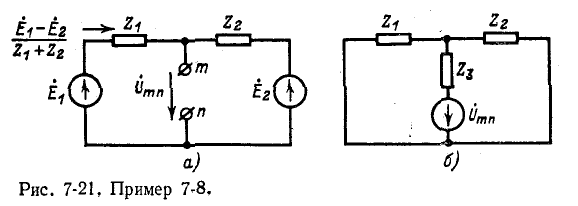
Пример 7-8.

Пользуясь теоремой об -эквивалентном источнике э,д. с., определить токи в ветвях схемы рис. 7-4.

Размыкание ветви и соответственно нахождение напряжения холостого хода могут быть произведены в любой из трех ветвей заданной электрической цепи. Рисунок 7-21 показан для случая размыкания ветви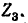

Напряжение холостого хода 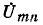находится в этом случае как разность э. д. с. 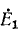падения напряжения оттока 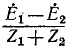в комплекс-ном сопротивлении 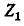(рис. 7-21,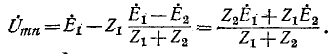
Под воздействием э. д. с. (]тп в схеме рис. 7-21,6 через комплексное. сопротивление 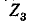идет ток

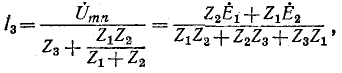
который разветвляется в 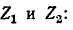через 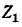проходит ток

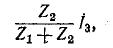
а через 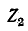— ток

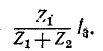
Искомые токи в ветвях 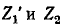определяются в результате сложения токов, проходящих в схемах рис. 7-21, а и б, т. е.

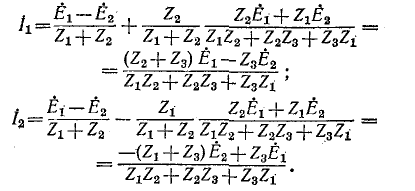
Данный пример иллюстрирует применение теоремы об эквивалентном источнике э. д. с. для вычисления токов в разных ветвях, причем не ставится цель получить решение кратчайшим путем.

 

Пример 7-9.

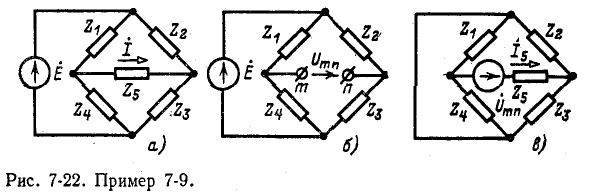
Пользуясь теоремой об эквивалентном источнике Э. Д. с., определить ток в диагональной ветви мостовой схемы рис. 7-22, а.

Разомкнув ветвь 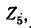находим напряжение холостого хода 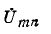как разность напряжений на участках 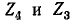(рис. 7-22, б):

Сопротивление между тип при Е = 0 и разомкнутой ветви 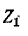равно (рис. 7-22, в):

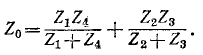
На основании (7-18)

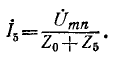
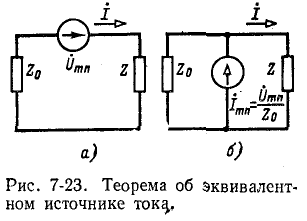
Теорема об эквивалентном источнике тока:

Ток в любой ветви тп линейной электрической цепи не изменится, если электрическую цепь, к которой подключена данная ветвь, заменить эквивалентным источником тока; ток этого источника должен быть 

равен току, проходящему между выводами m и n, замкнутыми накоротко, а внутренняя проводимость источника должна равняться входной проводимости пассивной электрической цепи со стороны выводов тип при разомкнутой ветви тп.

Данное положение вытекает из условия эквивалентности источников напряжения и тока, а именно:    источник

э. д. с., которая равна напряжению холостого хода 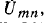а (рис. 7-23, а), может быть заме-

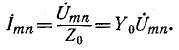
Последнее выражение есть не что иное, как ток, проходящий между выводами тип, замкнутыми накоротко (ток короткого замыкания). Искомый ток в цепи равен:

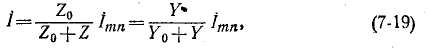
где

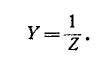
Если известно распределение токов в электрической цепи при закороченных выводах m и n, то распределение токов в цепи при включенной ветви Z может быть найдено посредством наложения на предыдуг щий режим тех токов, которые получаются в результате присоединения источника тока 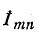 к ветви Z (когда остальная часть цепи пассивна).

При наличии в электрической цепи нескольких источников э. д. с. и тока одинаковой частоты ток короткого замыкания является линейной функцией заданных э. д. с. и токов источников.

Пример 7-10.

Пользуясь теоремой об эквивалентном источнике тока, определить ток 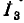в ветви 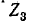схемы рис, 7-4,

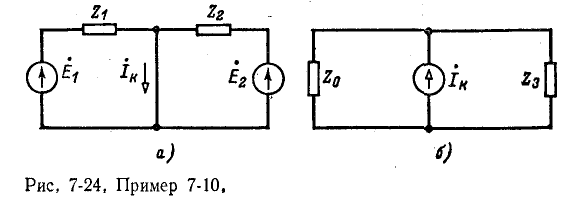
Ток эквивалентного источника равен току короткого замыкания 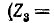0, рис, 7-24, а):

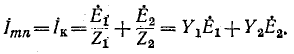
Комплексная проводимость эквивалентного источника равна 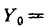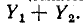Следовательно, на основании (7-19) искомый ток равен: