
Теорема о движении центра инерции в теоретической механике
Теорема о движении центра инерции:
Центром инерции, или центром масс, материальной системы называется геометрическая точка, определяемая координатами:
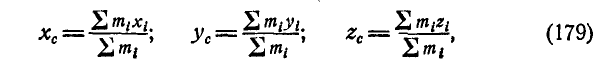
или векторно:
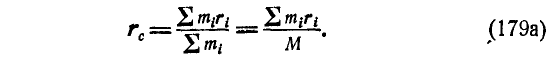
Умножив и разделив числитель и знаменатель правой части равенства (179а) на величину 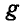 ускорения земного притяжения, получим известное из статики выражение радиуса-вектора, определяющего центр тяжести системы.
ускорения земного притяжения, получим известное из статики выражение радиуса-вектора, определяющего центр тяжести системы.
Отсюда следует, что центр инерции и центр тяжести суть два названий одной и той же точки. Однако понятие «центра инерции», или «центра масс», является более общим, чем понятие «центра тяжести».
При движении системы ее центр инерции также перемещается в пространстве. Посмотрим теперь, как происходит движение центра инерции.
Обозначим равнодействующую всех внешних сил, приложенных к 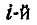 точке системы через
точке системы через 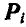 , а всех внутренних сил
, а всех внутренних сил 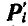 . Тогда дифференциальные уравнения движения точек системы будут:
. Тогда дифференциальные уравнения движения точек системы будут:
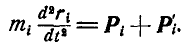
Произведя суммирование по всем точкам системы, будем иметь:
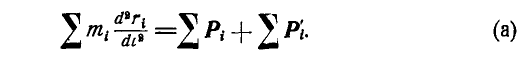
Умножая обе части равенства (179а) на М и беря вторую производную по t, найдем:
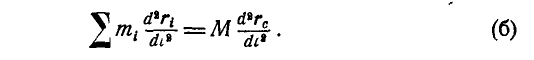
На основании равенств (а) и (б) имеем:
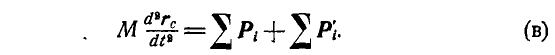
Первое слагаемое правой части уравнения (в) 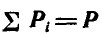 представляет главный вектор всех внешних сил, который находится по правилу многоугольника сил. Второе же слагаемое
представляет главный вектор всех внешних сил, который находится по правилу многоугольника сил. Второе же слагаемое 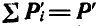 представляет главный вектор всех внутренних сил, который обращается в нуль в силу того, что действия и противодействия всех точек системы, взятых попарно, равны по величине и противоположны по направлению. Поэтому имеем окончательно:
представляет главный вектор всех внутренних сил, который обращается в нуль в силу того, что действия и противодействия всех точек системы, взятых попарно, равны по величине и противоположны по направлению. Поэтому имеем окончательно:
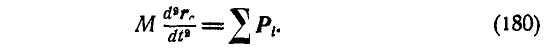
Уравнение (180) может быть записано также через проекции на координатные оси в виде следующих дифференциальных уравнений движения:
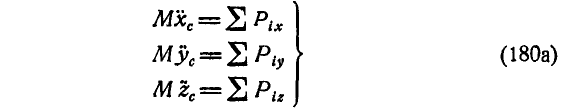
Эти дифференциальные уравнения выражают движение материальной точки С, имеющей массу М и находящуюся под действием внешних сил. Внутренние силы в правые части уравнений (180а) не входят, так как они по закону «действие равно противодействию» попарно уравновешиваются и дают сумму проекций на координатные оси, равную нулю.
Итак, центр инерции системы движется как материальная точка, в которой сосредоточена масса всей системы и на которую действует главный вектор всех внешних сил.
В этом заключается теорема о движении центра инерции. Изменить характер движения и положение центра инерции могут только внешние силы.
Так, если свободно летящая ракета, центр инерции которой движется по параболе (рис. 314), при воспламенении горючего разорвется в воздухе, то центр инерции осколков ракеты под действием все той же силы тяжести Q будет продолжать свое движение так, как если бы взрыва не было совсем. Изменение движения центра инерции ракеты произойдет только тогда, когда один из осколков упадет на землю. Точно так же, если человек будет идти по лодке, находящейся в спокойной воде, вперед, то лодка будет двигаться назад; центр же инерции системы (лодки и человека) будет оставаться на месте, и только сопротивление воды, являющееся внешней силой по отношению к системе, будет несколько влиять на смещение центра инерции.

Рис. 314.
При прыжке цирковой акробат не в силах изменить движения своего центра тяжести, какие бы телодвижения он ни делал в воздухе; только какое-либо внешнее препятствие может изменить характер движения его центра тяжести. Таких примеров можно привести множество.
Положим теперь, что на систему не действуют внешние силы, или их главный вектор равен нулю (что возможно при действии пар). В этом случае сумма проекций внешних сил на каждую из осей равна нулю и мы приходим к равенствам:
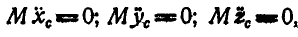
или
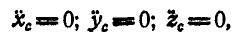
откуда
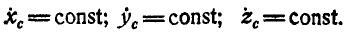
Итак, если главный вектор всех внешних сил, приложенных к системе, равен нулю, то центр инерции такой системы находится в покое или движется прямолинейно и равномерно.
В этом заключается теорема о сохранении движений центра инерции.
Задача №1
По наклонной плоскости, представляющей однородную треугольную призму весом 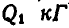 и свободно перемещаемой в горизонтальном направлении, катится однородный цилиндр весом
и свободно перемещаемой в горизонтальном направлении, катится однородный цилиндр весом 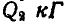 (рис. 315). Пренебрегая сопротивлениями, определить перемещение наклонной плоскости за время прохождения цилиндром всей длины ее, равной
(рис. 315). Пренебрегая сопротивлениями, определить перемещение наклонной плоскости за время прохождения цилиндром всей длины ее, равной 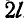 .
.
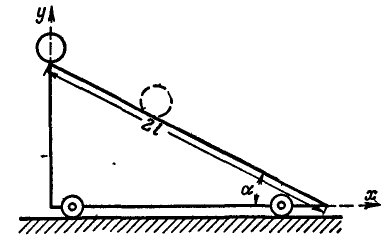
Рис. 315.
Решение. Пусть перемещение платформы за время прохождения цилиндром пути 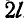 равно
равно 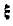 ; тогда абсциссы центра инерции всей системы по отношению к неподвижным осям х и у для начального и конечного положений цилиндра будут:
; тогда абсциссы центра инерции всей системы по отношению к неподвижным осям х и у для начального и конечного положений цилиндра будут:
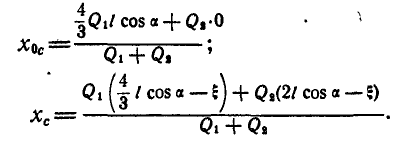
Сумма проекций всех внешних сил на ось х равна нулю, поэтому проекция центра инерции всей системы на ось х должна двигаться по оси х равномерно или быть в покое, если центр инерции находился вначале в покое (как это имеет место в нашем случае), поэтому 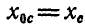 , откуда:
, откуда:
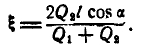
Задача №2
Однородный тонкий стержень АВ длиной 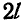 опирается концом А на гладкую горизонтальную плоскость (рис. 316). Стержень слегка отклоняют от вертикального положения, и, предоставленный самому себе, он падает под влиянием силы тяжести.
опирается концом А на гладкую горизонтальную плоскость (рис. 316). Стержень слегка отклоняют от вертикального положения, и, предоставленный самому себе, он падает под влиянием силы тяжести.
Какова траектория центра тяжести стержня, а также конца его В при падении?
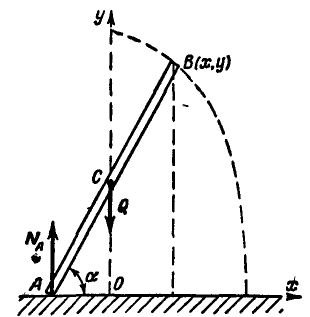
Рис. 316.
Решение. В момент падения стержня на него действуют две вертикальные силы: нормальная реакция плоскости 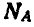 и вес стержня Q. Пусть ось Ох горизонтальна и ось стержня в начальном своем положении совпадает с осью Оy, тогда дифференциальные уравнения (180 а), движения центра инерции стержня будут:
и вес стержня Q. Пусть ось Ох горизонтальна и ось стержня в начальном своем положении совпадает с осью Оy, тогда дифференциальные уравнения (180 а), движения центра инерции стержня будут:
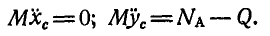
Интегрируем два раза первое уравнение:
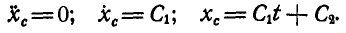
При 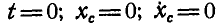 , откуда
, откуда 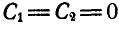 ; следовательно,
; следовательно, 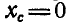 , т. е. центр инерции стержня все время движется по вертикали.
, т. е. центр инерции стержня все время движется по вертикали.
Так как 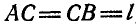 , то координаты конца В стержня соответственно равны:
, то координаты конца В стержня соответственно равны:
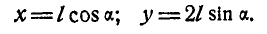
Исключая из этих уравнений 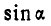 и
и 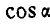 , находим, что траектория точки В эллипс:
, находим, что траектория точки В эллипс:
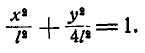
Задача №3
Посредине балки АВ, опирающейся на две шарнирные опоры А и В, укреплена станина весом 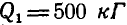 так, что центр тяжести станины
так, что центр тяжести станины 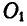 совпадает с осью балки. Через точку
совпадает с осью балки. Через точку 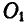 перпендикулярно к плоскости чертежа проходит ось вращения груза D весом
перпендикулярно к плоскости чертежа проходит ось вращения груза D весом 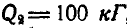 , делающего
, делающего 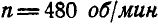 вокруг своей оси. Пренебрегая массой балки, определить амплитуду ее вынужденных колебаний; если известно, что для прогиба балки на 1 см нужна сила 5000 кГ и радиус вращения груза D равен
вокруг своей оси. Пренебрегая массой балки, определить амплитуду ее вынужденных колебаний; если известно, что для прогиба балки на 1 см нужна сила 5000 кГ и радиус вращения груза D равен 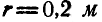 (рис. 317).
(рис. 317).
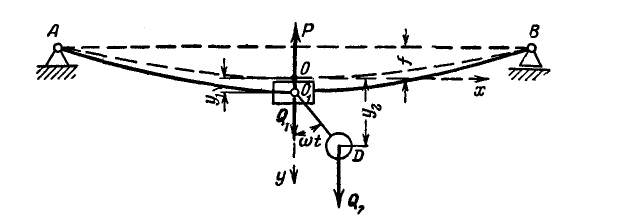
Рис. 317.
Решение. Пусть под действием статической нагрузки центр станины переместится в положение О, а во время колебаний в 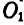 , определяемое расстоянием
, определяемое расстоянием 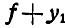 , где
, где 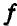 — прогиб балки от статического загружения ее силами
— прогиб балки от статического загружения ее силами 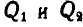 , а
, а 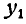 — дополнительный прогиб балки, получившийся вследствие ее колебания. Проведя через точку О, соответствующую статическому прогибу балки, координатные оси, составим по отношению к оси дифференциальное уравнение движения центра инерции системы, состоящей из двух материальных точек — станины и груза D:
— дополнительный прогиб балки, получившийся вследствие ее колебания. Проведя через точку О, соответствующую статическому прогибу балки, координатные оси, составим по отношению к оси дифференциальное уравнение движения центра инерции системы, состоящей из двух материальных точек — станины и груза D:
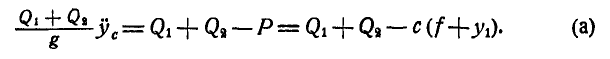
Здесь 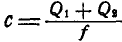 — жесткость балки.
— жесткость балки.
Из чертежа видно, что 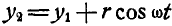 . Определим теперь ординату центра инерции системы:
. Определим теперь ординату центра инерции системы:
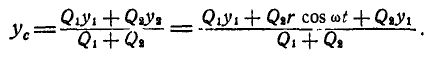
Подставив вместо 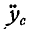 найденное его значение из последнего равенства в уравнение (а), получим:
найденное его значение из последнего равенства в уравнение (а), получим:
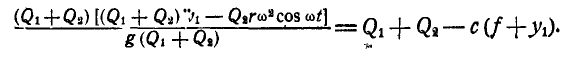
Отсюда, после простых преобразований, имеем:
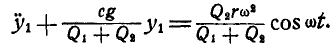
Сравнивая это уравнение с формулой (162)
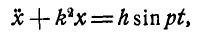
видим, что вынужденные колебания станины происходят с амплитудой, определяемой равенством:
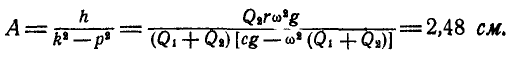
Здесь:
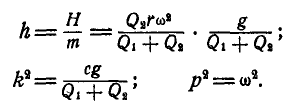
| Рекомендую подробно изучить предмет: |
| Ещё лекции с примерами решения и объяснением: |
- Теорема количества движения
- Теорема моментов количества движения
- Теорема кинетической энергии
- Условие равновесия системы сходящихся сил в геометрической форме
- Сложение движений твердого тела в теоретической механике - формулы и определения с примерами
- Динамика материальной точки
- Движение материальной точки
- Аналитическая статика