Теорема моментов количества движения в теоретической механике

Теорема моментов количества движения:

Моментом количества движения системы относительно некоторой точка О называется геометрическая сумма моментов количества движения всех материальных точек системы относительно той же точки.

Обозначим момент количества движения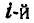

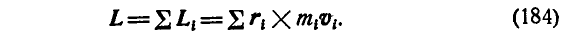
Из динамики точки мы знаем, что теорема моментов количества движения для 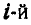точки системы может быть представлена так:

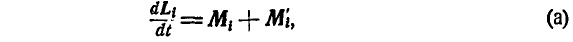
где 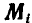 — момент внешних сил, приложенных к 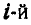точке системы,

    а 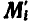— момент всех сил, с которыми остальные точки системы действуют на 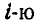точку. Равенство (а) можно написать для каждой точки системы. Складывая все эти равенства, получим:

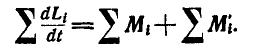
Но так как 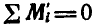в силу того, что внутренние силы попарно уравновешиваются и геометрическая сумма моментов их относительно любой точки обращается в нуль, то можем написать:

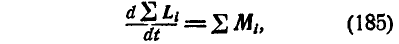
или окончательно:

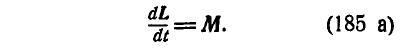
Это равенство и выражает теорему моментов количества движения системы, которая читается так:

Первая производная пo времени от вектора момента количества движения системы относительно точки равна взятому относительно той же точки главному моменту всех внешних сил. Непосредственно из равенства (185 а) следует, что главный момент внешних сил можно рассматривать как скорость конца вектора, представляющего момент количества движения системы (рис. 323).

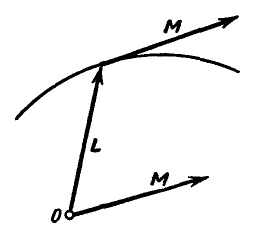
Рис. 323.

Векторное равенство (185) равносильно трем скалярным, получаемым, путем проектирования его на неподвижные координатные оси:

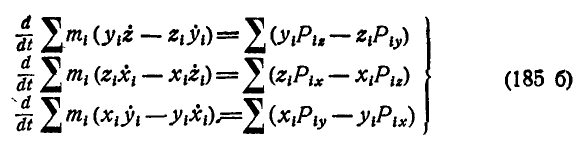
Предположим теперь, что момент внешних сил относительно одной из осей, например 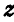, обращается в нуль, тогда, полагая правую часть третьего из равенств (185 б) равной нулю, найдем для этого уравнения первый интеграл

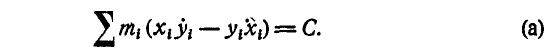
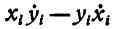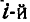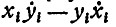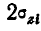Но мы уже знаем, что согласно (156 б) выражение представляет удвоенную секторную скорость точки в плоскости ху, поэтому, заменяя через , найдем:

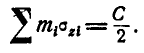
Итак, если связи системы допускают вращение ее около неподвижной оси, причем сумма моментов внешних сил относительно этой оси равна нулю, то сумма произведений масс точек системы на векторные скорости проекций этих точек на плоскость, перпендикулярную к оси вращения, есть величина постоянная.

Из уравнения (а) следует, что если С=0, то 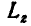тоже нуль. Поэтому, например, если человек, стоя спокойно с вытянутыми горизонтальнб руками на горизонтальной платформе, могущей без трения вращаться вокруг вертикальной оси, поворачивает руки на некоторый угол, его тело вместе с платформой поворачивается в обратную сторону. Как только человек прекращает поворачивать руки, то платформа вместе с телом вновь становится неподвижной. Указанное явление объясняется тем, что при повороте рук создается некоторый момент количества движения, который в сумме с моментом количества движения тела и платформы (поворачивающимися в обратную сторону) должен быть равен нулю, так как в начальный момент .

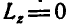Предположим теперь, что внешние силы отсутствуют, или их главный момент относительно некоторой точки равен нулю (что происходит, например, при действии на точки системы центральных сил). Это приводит нас к тому, что М=0, а следовательно, L=const.

Итак, если внешние силы отсутствуют или если их главный момент относительно точки, или, что то же, относительно осей х, у и z, проходящих через эту точку, равен нулю, то момент количества движения системы остается постоянным по величине и направлению.

Полагая в уравнениях (185 б) правые части равными нулю, получим первые интегралы этих уравнений:

• Заказать решение задач по теоретической механике

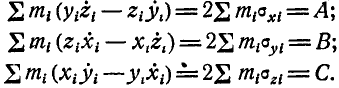
Задача №1

На ободе массивного кольца весом 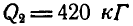и радиусом 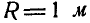в точке А стоит человек, вес которого 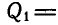60 кГ. Кольцо может вращаться вокруг вертикальной оси z (рис. 324). В некоторый момент человек начинает идти по кольцу с постоянной относительной скоростью 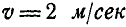. Какова будет при этом угловая скорость вращения кольца.

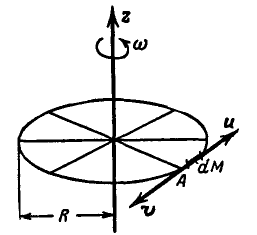
Рис. 324.

Решение. Все внешние силы, приложенные к системе (кольцу и человеку), параллельны оси z, поэтому 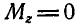и 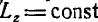. Так как в начальный момент система находится в покое, то .

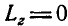При движении человека по кольцу по часовой стрелке (по отношению к оси z) кольцо начинает вращаться против часовой стрелки. Поэтому абсолютная скорость человека равна разности: , где 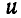— окружная скорость кольца. Момент количества движения человека по отношению к оси z будет:

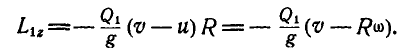
Для вычисления момента количества движения кольца относительно той же оси z выделим элемент кольца массой dM; тогда момент количества движения элемента:

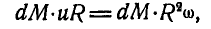
а всего кольца:

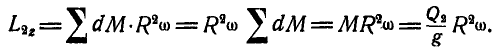
При движении человека по кольцу момент количества движения системы, равный вначале нулю, остается неизменном, а поэтому:

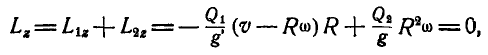
откуда

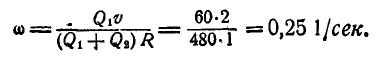
Задача №2

Стержень, по которому могут перемещаться два одинаковых груза А и В весом Q кГ каждый, вращается вокруг вертикальной оси, делая 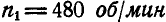. Грузы скреплены между собой нитью и расположены симметрично по отношению к оси вращения на взаимном расстоянии 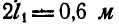(рис. 325). В некоторый момент нить пережигают и грузы, отодвинувшись к краям стержня, устанавливаются на расстоянии 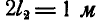м один от другого. Пренебрегая массой стержня, определить его новое число оборотов в минуту .

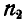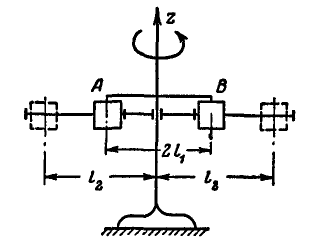
Рис. 325.

Решение. На систему, состоящую из двух грузов, все время действуют вертикальные силы, а поэтому 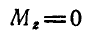и, следовательно, .

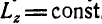Отсюда следует, что моменты количества движения системы 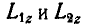относительно оси z до пережигания нити и после пережигания равны между собой, т. е. , или:

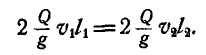
Но, так как:

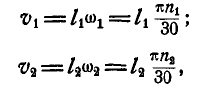
то

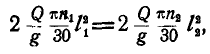
откуда

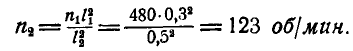
Нами была выведена теорема моментов количества движения системы по отношению к неподвижным координатным осям. Покажем теперь, что эта теорема применима и по отношению к координатным осям, имеющим начало в центре инерции системы и движущимся вместе с ним поступательно.

Пусть положение центра инерции С по отношению к неподвижным осям х, у и z определяется радиусом-вектором 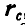, а положение 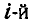точки системы — радиусом-вектором 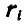(рис. 326). Пусть также положение 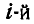точки по отношению к подвижным осям 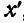, , 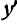, 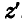движущимся поступательно вместе с центром инерции, определяется радиусом-вектором 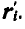Мы знаем, что теорема моментов количества движения системы по отношению к неподвижным осям х, у, z выражается:

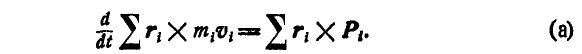
Из чертежа видно, что 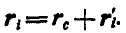Продифференцируем ато равенство по t; тогда:

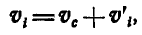
где 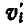— скорость 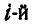точки по отношению к центру инерции.

Подставляя вместо 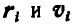найденные их значения в уравнение (а), получим:

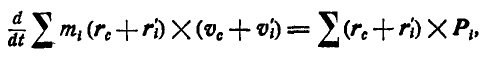
или, после перемножения:

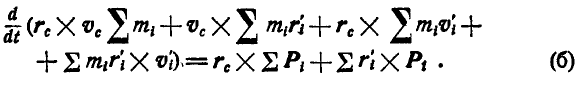
Множители общие для всех точек, как, например, 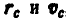, вынесены за знак суммы.

Здесь:

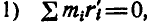
так как 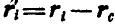, а отсюда:

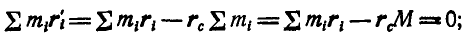
См. координаты центра инерции.

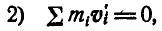
так как 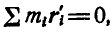, а следовательно,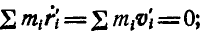

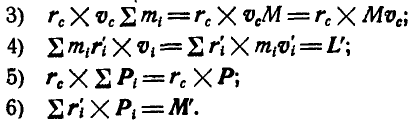
Векторы 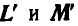 представляют соответственно момент количества движения системы и главный момент всех внешних сил, приложенных к системе относительно ее центра инерции.

После проделанных нами преобразований уравнение (б) принимает вид:

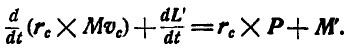
Но так как

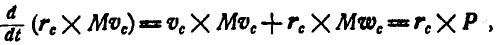
то окончательно имеем: 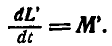 Здесь в силу коллинеарности векторов 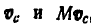, а 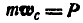 —по теореме движения центра инерции.

Итак, производная по времени от вектора момента количества движения системы в ее движении по отношению к центру инерции равна главному моменту всех внешних сил, приложенных к системе относительно ее центра инерции.