
Теорема компенсации
Теорема компенсации:
Токи в электрической цепи не изменятся, если любой участок цепи заменить э. д. с., равной напряжению на данном участке и направленной навстречу току, проходящему по данному участку.
Справедливость этого положения, носящего название теоремы компенсации, вытекает из того, что любое из слагающих падения напряжений,- входящих в уравнение по второму закону Кирхгофа, может быть
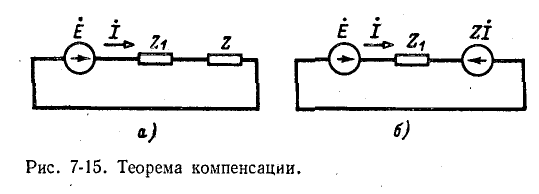
• Иллюстрацией сказанного выше служит рис. 7-15; уравнение по второму закону Кирхгофа, записанное для схемы рис. 7-15, а как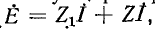
Последней записи уравнения соответствует схема рис. 7-15, б, в которой вместо сопротивления Z включена э. д. с. Zl, направленная противоположно току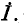
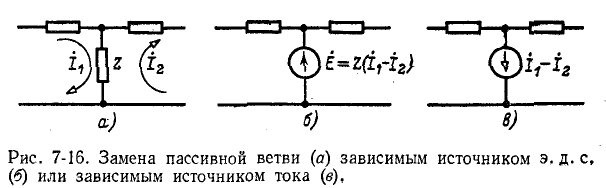
Данная теорема справедлива и для разветвленных электрических цепей. Рисунки 7-16, а и б иллюстрируют возможность замены комплексного сопротивления Z источником э. д. с. 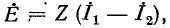 действующим навстречу току
действующим навстречу току 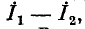 проходящему через сопротивление Z.
проходящему через сопротивление Z.
Вместо источника э. д. с. может быть включен источник тока (рис. 7-16, в), обусловливающий прохождение между
узлами / и 2 того же тока, что и в схеме рис. 7-16, а; токи и напряжения в остальной части цепи при этом не меняются.
Следует заметить, что э. д. с. или ток источника, заменяющего собой участок цепи, определяется в зависимости от тока, проходящего через данный участок. При изменении параметров остальной части цепи ток на данном участке в общем случае изменяется, и поэтому указанный выше источник не является самостоятельным, а представляет собой так называемый зависимый, или неавтономный, источник.
Применение теоремы компенсации облегчает изучение свойств линейных электрических цепей./Гак, заменяя "какой-либо участок цепи зависимым источником э. д. с. или тока
и пользуясь методом наложения, легко убедиться в том, что напряжения и токи в остальной части цепи являются линейными функциями напряжения на данном- участке или тока, проходящего через него. Например, если при изменении комплексного сопротивления Z в какой-либо ветви изменяется ток  в этой ветви, то ток
в этой ветви, то ток  в какой-либо другой ветви связан с
в какой-либо другой ветви связан с 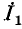 линейной функциональной зависимостью
линейной функциональной зависимостью
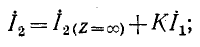
здесь 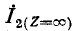 ) — значение тока
) — значение тока 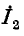 при
при 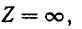 т. е. при разомкнутой первой ветви.
т. е. при разомкнутой первой ветви.
Комплексный коэффициент К находится из условия, что при Z = О

поэтому
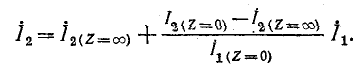
| Рекомендую подробно изучить предметы: |
| Ещё лекции с примерами решения и объяснением: |
- Теорема об изменении токов в электрической цепи при изменении сопротивления в одной ветви
- Теорема об эквивалентном источнике
- Применение матриц к расчету электрических цепей
- Дуальные цепи
- Метод узловых и контурных уравнений
- Метод эквивалентного генератора
- Теоремы теории цепей
- Теорема обратимости (или взаимности)