
Теорема количества движения в теоретической механике
Теорема количества движения:
Количеством движения системы называется вектор, равный геометрической сумме векторов количеств движения всех материальных точек системы:
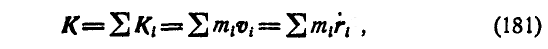
где 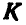
В целях сокращения записи здесь и ниже пределы суммирования 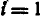 и
и 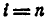 опущены.
опущены.
При движении системы ее вектор количества движения изменяется. Найдем это изменение.
Обозначим равнодействующую всех внешних сил, приложенных к 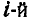 точке системы через
точке системы через 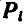 , а всех сил, с которыми остальные точки системы действуют на
, а всех сил, с которыми остальные точки системы действуют на 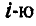 точку, — через
точку, — через 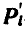 . Тогда для выбранной точки основное уравнение динамики будет:
. Тогда для выбранной точки основное уравнение динамики будет:
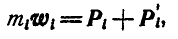
или
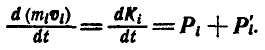
Напишем теперь такие геометрические равенства для всех точек системы и просуммируем их; тогда получим:
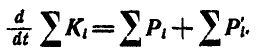
Но так как 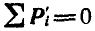 в силу того, что внутренние силы попарно уравновешиваются, т. е. их геометрическая сумма равна нулю, то получаем окончательно:
в силу того, что внутренние силы попарно уравновешиваются, т. е. их геометрическая сумма равна нулю, то получаем окончательно:
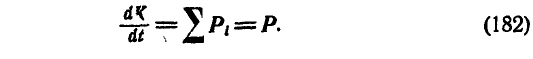
Итак, в каждый момент первая производная по времени от вектора количества движения системы равна главному вектору всех внешних сил.
В этом заключается теорема количества движения системы. Проинтегрировав обе части уравнения (182), найдем:
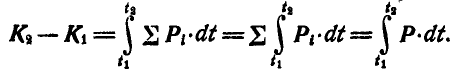
Как было указано, в динамике точки
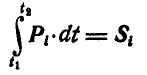
есть импульс силы 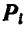 ;
;
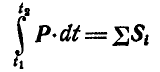
представляет собой геометрическую сумму импульсов; обозначим 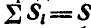 . Таким образом, теорема количества движения системы может быть представлена также в следующей форме:
. Таким образом, теорема количества движения системы может быть представлена также в следующей форме:
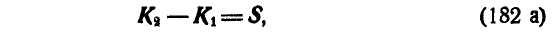
т. е. геометрическое приращение количества движения системы равно геометрической сумме импульсов внешних сил.
Если 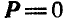 , то
, то 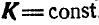 . Важно отметить, что подобно тому, как внутренние силы не могут изменить движения центра инерции системы, так и количество движения системы не меняется в случае уравновешивающихся внешних сил. Так например, если человек идет вперед по платформе, свободно перемещаемой по абсолютно гладкой плоскости, то платформа будет перемещаться назад; при этом скорости движения человека и платформы направлены в разные стороны и их отношение обратно пропорционально массам человека и платформы, так как количество движения системы остается все время постоянным. В этом случае, как мы знаем, и положение проекции центра инерции системы на плоскость платформы не меняется.
. Важно отметить, что подобно тому, как внутренние силы не могут изменить движения центра инерции системы, так и количество движения системы не меняется в случае уравновешивающихся внешних сил. Так например, если человек идет вперед по платформе, свободно перемещаемой по абсолютно гладкой плоскости, то платформа будет перемещаться назад; при этом скорости движения человека и платформы направлены в разные стороны и их отношение обратно пропорционально массам человека и платформы, так как количество движения системы остается все время постоянным. В этом случае, как мы знаем, и положение проекции центра инерции системы на плоскость платформы не меняется.
Векторное равенство (182) можно представить в виде трех-скалярных равенств путем проектирования его на координатные оси х, у и z:
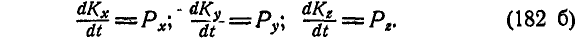
Теорема количества движения находит большое применение при изучении движения сплошных систем (жидкости и пр.), а также в теории удара.
Задача №1
Найти количество движения однородного цилиндра, вращающегося вокруг геометрической оси с угловой скоростью  .
.
Решение. Из равенства (179 а), определяющего положение центра инерции системы, находим:
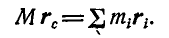
Продифференцируем это равенство по t:
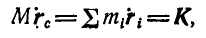
или
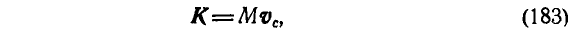
т. е. количество движения системы равно произведению ее массы на скорость центра инерции и направлено по этой скорости.
Так как в нашем случае центр тяжести цилиндра, совпадающий с осью вращения, неподвижен, то отсюда и количество движения цилиндра равно нулю.
Задача №2
Найти импульс сил, приложенных к диску, катящемуся без скольжения по кpyгy, за время, когда диск пройдет путь, равный четверти окружности и перейдет из положения I в положение II (рис. 320). Вес диска 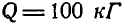 и скорость его центра инерции
и скорость его центра инерции 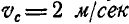 .
.
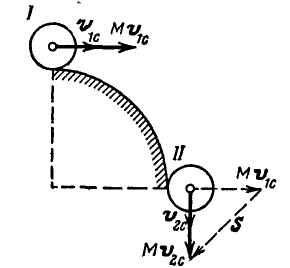
Рис. 320.
Решение. Применяя теорему количества движения в конечной форме (182 а), получим:
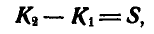
а так как 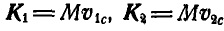 , то:
, то:
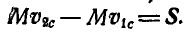
Построив векторный треугольник, находим величину и направление 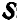 :
:
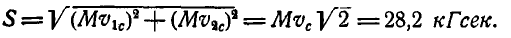
Задача №3
Резервуар для хранения воды весом 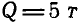 наполнен водой в количестве
наполнен водой в количестве 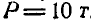 . В некоторый момент заслонку А, прикрывающую отверстие, имеющееся в днище резервуара, отодвигают, и вода будет свободно вытекать через отверстие диаметром
. В некоторый момент заслонку А, прикрывающую отверстие, имеющееся в днище резервуара, отодвигают, и вода будет свободно вытекать через отверстие диаметром 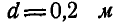 . Пренебрегая гидравлическими сопротивлениями и скоростями частиц воды внутри резервуара, вычислить давление N резервуара на опоры в момент полного открытия заслонки. Среднюю скорость, с которой вода будет вытекать через отверстия после открытия заслонки, принять
. Пренебрегая гидравлическими сопротивлениями и скоростями частиц воды внутри резервуара, вычислить давление N резервуара на опоры в момент полного открытия заслонки. Среднюю скорость, с которой вода будет вытекать через отверстия после открытия заслонки, принять 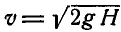 , где
, где 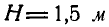 (рис. 321).
(рис. 321).
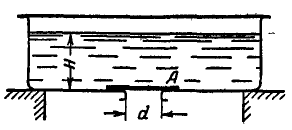
Рис. 321.
Решение. Применяем теорему количества движения в проек циях на вертикальную ось у:
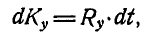
где 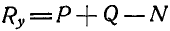 —проекция равнодействующей всех внешних сил, приложенных к системе.
—проекция равнодействующей всех внешних сил, приложенных к системе.
Считая, что количество воды в резервуаре в момент открытия заслонки не меняется, получим:
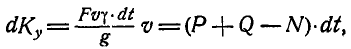
где 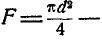 площадь отверстия.
площадь отверстия.
Отсюда
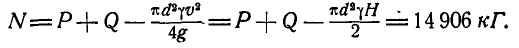
Задача №4
Вода входит в неподвижный канал переменного сечения, симметричный относительно вертикальной плоскости, со скоростью 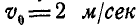 под углом
под углом 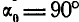 к горизонту; сечение канала при входе
к горизонту; сечение канала при входе 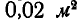 ; вода выходит из канала под углом
; вода выходит из канала под углом 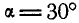 к горизонту со скоростью
к горизонту со скоростью 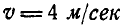 (рис. 322). Определить горизонтальную составляющую давления, которое вода оказывает на сечение канала.
(рис. 322). Определить горизонтальную составляющую давления, которое вода оказывает на сечение канала.
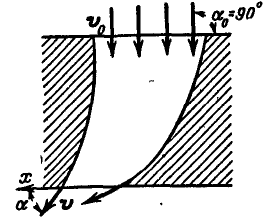
Рис. 322.
Решение. Применяем теорему количества движения в проекциях на ось х:
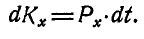
Так как .количество воды, поступающей в канал и выходящей из него за одно и то же время, постоянно, то отсюда:
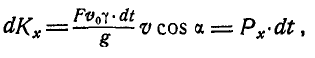
где F — площадь входного сечения;
или
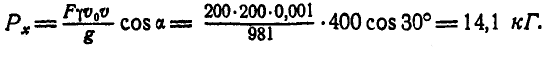
| Рекомендую подробно изучить предмет: |
| Ещё лекции с примерами решения и объяснением: |
- Теорема моментов количества движения
- Теорема кинетической энергии
- Условие равновесия системы сходящихся сил в геометрической форме
- Условия равновесия системы сходящихся сил в аналитической форме
- Динамика материальной точки
- Движение материальной точки
- Аналитическая статика
- Теорема о движении центра инерции