Теорема кинетической энергии в теоретической механике

Теорема кинетической энергии:

Выше уже отмечалось, что действительные перемещения находятся в числе возможных в том случае, когда связи стационарны.

Если система подчинена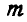

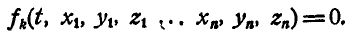
Дифференцируя это уравнение в предположении, что t постоянно, найдем уравнение, которому должны удовлетворять

проекции возможных перемещений системы при наличии 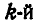связи:

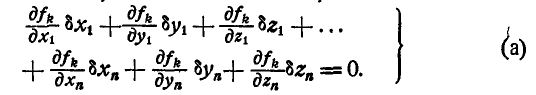
Условие, которому должны удовлетворять проекции действительных перемещений, получим путем дифференцирования уравнения 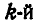связи в предположении, что t изменяется:

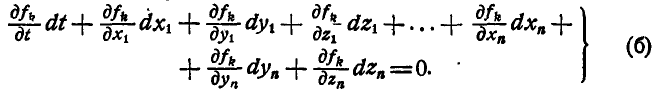
Действительные перемещения будут находиться в числе возможных при условии, когда 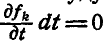. Легко видеть (см. § 31 и 39), что общее уравнение динамики при наличии двусторонних связей принимает вид:

 

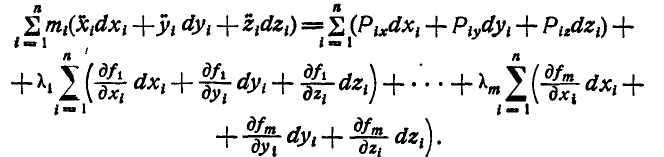
При 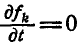все суммы при — нули в силу равенств (а) и (б). Вспоминая вывод теоремы кинетической энергии для точки, найдем:

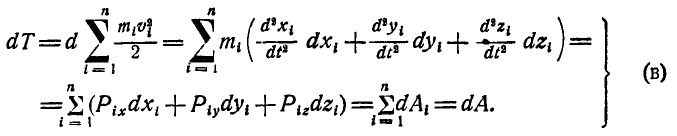
Выражение

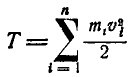
называется кинетической энергией системы.

Мы получили следующую теорему кинетической энергии системы в дифференциальной форме: приращение кинетической энергии на бесконечно малом перемещении системы равно сумме элементарных работ всех внутренних и внешних действующих сил на этом же перемещении при связях, не зависящих от времени.    

Чтобы определить изменение кинетической энергии системы при переходе ее из положения 1 в положение 2, проинтегрируем обе части уравнения (в):

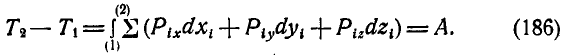
Здесь 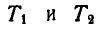— кинетическая энергия системы в крайних ее положениях.

Итак, при переходе системы из одного положения в другое изменение кинетической энергии системы равно сумме работ всех сил, приложенных к точкам системы.

В этом заключается теорема кинетической энергии движущейся системы.

Рассмотрим теперь движение системы, происходящее в консервативном поле.

Общее выражение силовой функции в этом случае будет:

Если система находится только под действием консервативных сил, то, как мы знаем, элементарная работа этих сил выражается полным дифференциалом силовой функции:

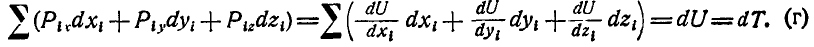
Уравнение (186), выражающее теорему кинетической энергии, в этом случае принимает вид:

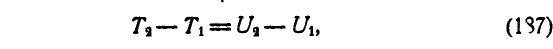
т. е. изменение кинетической энергии системы при некотором ее перемещении равно разности значений силовой функции для крайних положений системы.

Мы уже знаем, что силовая функция, взятая с обратным знаком, называется потенциальной энергией.

Полагая в уравнении (187) 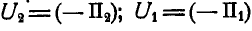, найдем:

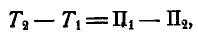
или

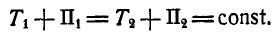
Это уравнение и выражает закон сохранения энергии системы и читается так:

В каждый момент сумма кинетической и потенциальной энергии системы, движущейся в консервативном поле, постоянна.

• Заказать решение задач по теоретической механике

Задача №1

Груз 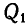соединен с двумя другими грузам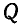и и 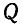при помощи нити, перекинутой через два ничтожно малых блока, расположенных на одной горизонтали и на расстоянии 2а один от другого (рис. 327). Первоначально груз 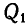удерживается посредине между блоками, а затем отпускается без начальной скорости. Принимая все три груза за материальные точки, определить величину А опускания груза 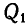, соответствующую статическому равновесию.

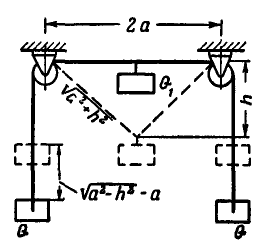
Рис. 327.

Решение. Применим теорему кинетической энергии (186), приняв за первое положение системы ее начальное положение, а за второе — то, когда груз 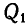опустится на величину h.

Кинетическая энергия системы (трех грузов) в начале и конце движения равна нулю, а поэтому из уравнения (186) следует, что должна быть также равна нулю и сумма работ, совершаемых силам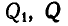и и 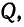 т. е.:

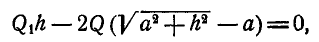
откуда

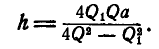
Для конечного 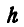необходимо, чтобы было выполнено условие

Задача №2

К концам тонкой нити, перекинутой через ролик, прикреплены два груза 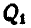и 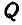, которых 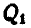свободно висит, a 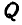может свободно скользить вдоль вертикальной направляющей (рис. 328). Груз 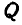удерживается сначала в положении 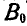, а затем опускается без начальной скорости. Считая грузы за материальные точки, определить скорость груза  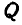в зависимости от у.

Рис. 328.

Решение. Применим теорему кинетической энергии между двумя положениями системы, когда груз Q находится в положении 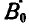и когда он находится в положении В, определяемом расстоянием у. Так как в начале кинетическая энергия системы равна нулю, то 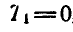, и уравнение (186) принимает вид 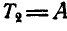, или

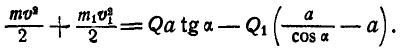
Из чертежа видно, что 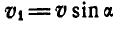, а отсюда, произведя замену, найдем:

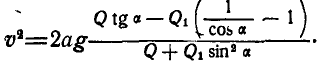
Подставим теперь значение 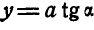, тогда:

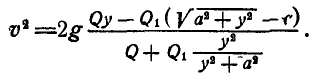
При решении многих задач, связанных с вычислением кинетической энергии, бывает полезно абсолютное движение системы по отношению к неподвижным осям 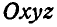(рис. 329) представить в виде двух движений — переносного поступательного вместе с центром инерции С, или, что то же, вместе с осями 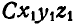, движущимися параллельно осям Oxyz, и относительного движения вокруг центра инерции С, т. е. по отношению к осям .

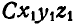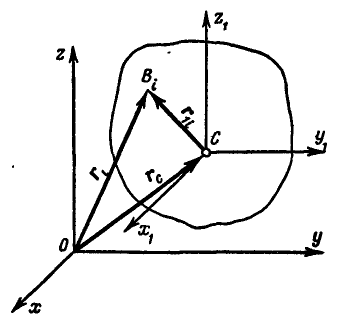
Рис. 329.

Пусть положения центра инерции С и какой-либо точки системы 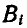по отношению к осям Oxyz определяются радиусами-векторами 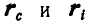, а положение точки 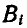по отношению к осям 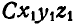радиусом-вектором 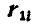. Тогда имеем: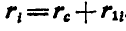

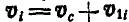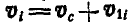Беря производную по времени от обеих частей равенства, найдем или , где 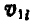—относительная скорость точки 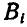по отношению к осям 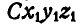или, что то же, к центру инерции С.

Так как кинетическая энергия системы будет:

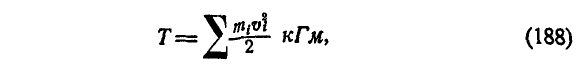
то, подставляя вместо 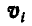, найденное значение, получим:

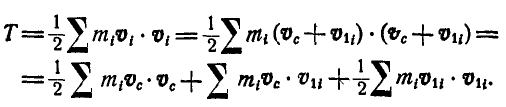
Покажем, что

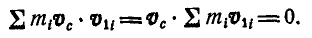
Действительно, применим равенство (179,а) по отношению к осям 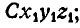 тогда

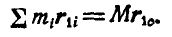
Но так как 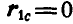, то

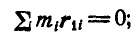
следовательно:

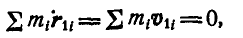
а также

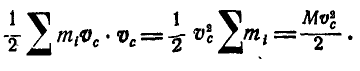
Окончательно имеем:

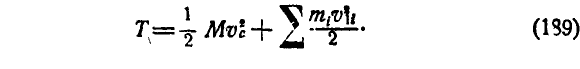
Следовательно, кинетическая энергия системы равна сумме кинетической энергии центра инерции в предположении, что в нем сосредоточена масса всей системы и кинетической энергии в ее относительном движении по отношению к поступательно движущимся осям координат с началом в центре инерции.

В этом заключается теорема Кенига.

Большое количество задач на применение последних двух общих теорем динамики будет приведено в следующей главе — «Динамика твердого тела».