Тело на сферической и стержневых опорах в теоретической механике

Тело на сферической и стержневых опорах:

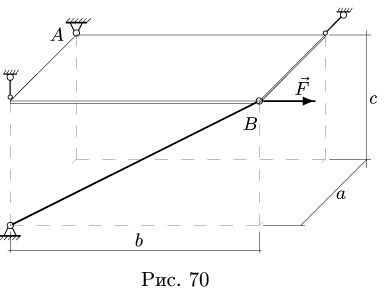
Постановка Задачи. Горизонтальная однородная прямоугольная полка имеет, в одной точке сферическую опору и поддерживается двумя невесомыми, шарнирно закрепленными по концам, стержнями (горизонтальным и вертикальным) и наклонной подпоркой. К полке приложена сила, направленная вдоль одного из ее ребер. Определить реакции опор.

План решения:

1.Рассматриваем равновесие полки. Действие на полку опорных стержней заменяем их реакциями. Реакции стержней направляем вдоль их осей. Выбираем оси координат с началом в сферической опоре. Реакцию сферической опоры раскладываем на три составляющие вдоль выбранных осей.

2.Составляем систему уравнений равновесия (три уравнения в проекциях на оси и три уравнения моментов относительно осей). Решаем полученную систему.

3.Выполняем проверку решения, подставляя найденные значения в уравнение моментов относительно какой-либо дополнительной оси.

Пример. Горизонтальная однородная полка весом G = 6 кН имеет в точке А сферическую опору и поддерживается двумя невесомыми, шарнирно закрепленными по концам, стержнями (горизонтальным и вертикальным) и подпоркой в точке В (рис. 70). К этой же точке приложена сила F = 5 кН, направленная вдоль одного из ребер полки.

Даны размеры 

1. Рассматриваем равновесие полки. Действие на тело опорных стержней заменяем их реакциями. Реакция — вертикальная, — горизонтальная вдоль бокового ребра полки.

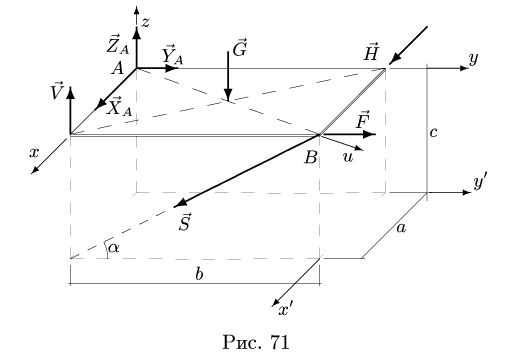
Усилие 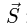в подпорке направлено вдоль стержня. В сферическом шарнире А имеется три составляющие реакции 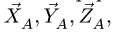которые направляем по осям координат. Так как полка однородная, ее центр тяжести совпадает с геометрическим центром. Сюда приложен вес 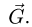Начато системы координат 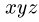помещаем в точку А (рис. 71).

2. Составляем систему уравнений равновесия, состоящую из трех уравнений проекций на оси координат всех сил, действующих на полку, и трех уравнений моментов относительно этих же осей (аналогичные уравнения см. § 4.4, с. 103):

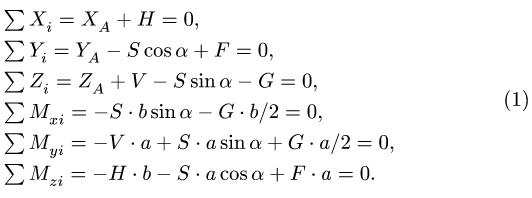
Так как начато координат находится в сферической опоре, система уравнений равновесия разделяется и становится проще. Из уравнений моментов можно найти независимо от других три неизвестные реакции S, Н и V.

Вычисляем значения тригонометрических функций:

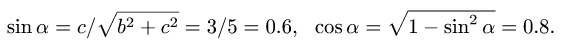
Из системы (1), находим реакции и заносим их в таблицу (в кН):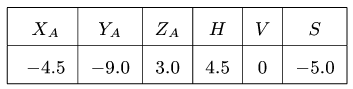

3. Выполняем проверку решения, подставляя найденные значения в уравнение моментов относительно дополнительных осей 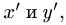проведенных параллельно соответствующим осям исходной системы координат:

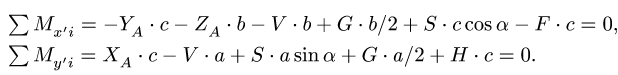
Замечание. Из решения системы (1) получается V =0. В этом можно убедиться сразу из уравнения моментов относительно дополнительной оси 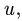лежащей на диагонали полки АВ (рис. 71). Действительно, все векторы, кроме 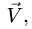пересекают эту ось и их моменты равны нулю. Уравнение принимает простой вид 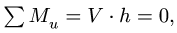где 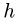— некоторое плечо реакции 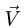относительно оси АВ. Не вычисляя 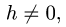получаем V = 0.4.6.