Тела вращения: цилиндр, конус, шар с примерами

Тела вращения: цилиндр, конус, шар:

Еще один важный класс пространственных фигур - это тела вращения. В него входят цилиндр, конус и шар.

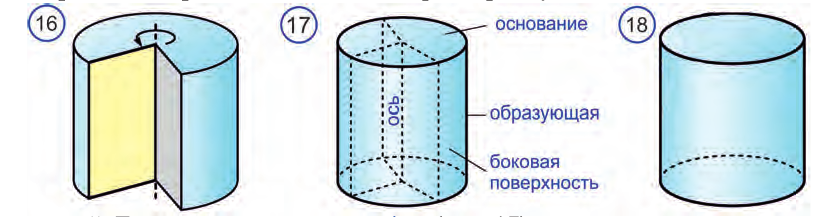
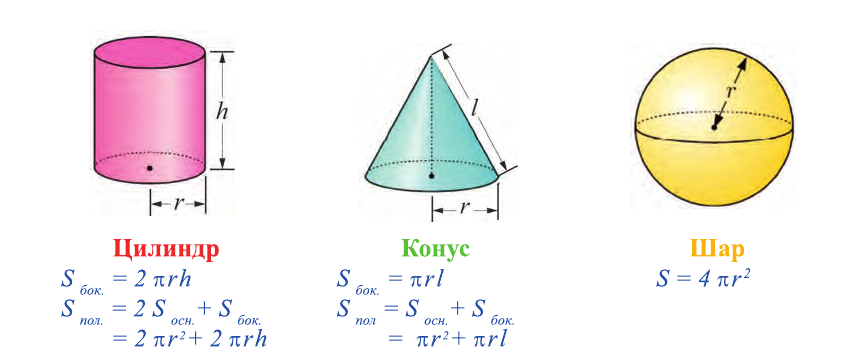
Тело, полученное при вращении прямоугольника вокруг одной из своих сторон, называется цилиндром (рис. 16-18).

При таком вращении одна из сторон прямоугольника остается неподвижной. Ее называют осью цилиндра (рис. 17).

Сторона, противоположная оси, поверхность цилиндра, а саму сторону называют образующей цилиндра.

Каждая из оставшихся сторон прямоугольника при этом вращении образует круговую поверхность. Эти круги называют основаниями цилиндра.

Тело, полученное при вращении прямоугольного треугольника вокруг одного из катетов, называют конусом (рис. 19 - 21). А этот катет осью конуса.

Другой катет прямоугольного треугольника образует при этом вращении круг, называемый основанием, гипотенуза образует боковую поверхность конуса, а саму гипотенузу называют образующей конуса. Кроме того, неподвижную вершину треугольника называют вершиной конуса (рис. 20).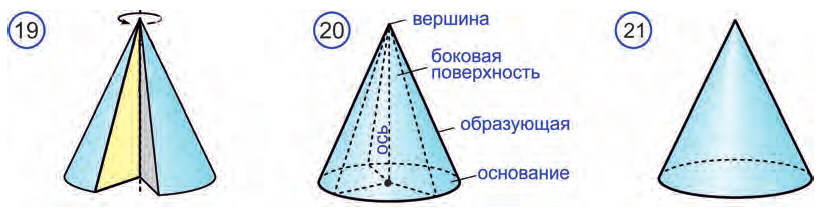

Теорема 1.3. Площадь боковой поверхности конуса равна произведению половины длины окружности основания на его образующую.

Доказательство. Пусть заданы радиус основания конуса r и образующая l (рис 22). Развернем боковую поверхность конуса на плоскость. В результате получим сектор круга радиуса l (рис. 23). Найдем центральный угол ф этого сектора (рис. 21). Этот угол опирается на дугу сектора, равного длине окружности основания -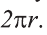

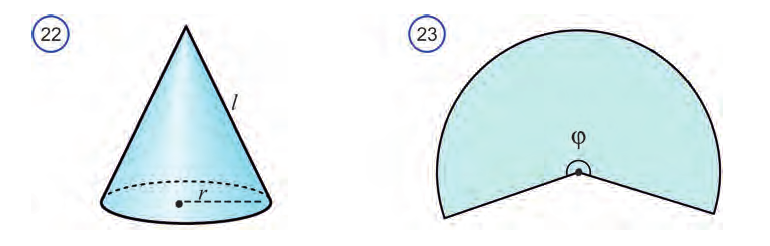
Известно, что, длина окружности радиуса l равна 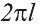и она стягивает центральный угол в 360°. В результате получим пропорцию: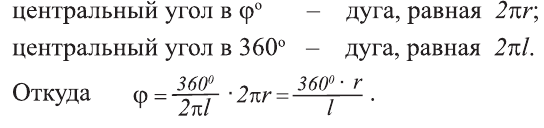

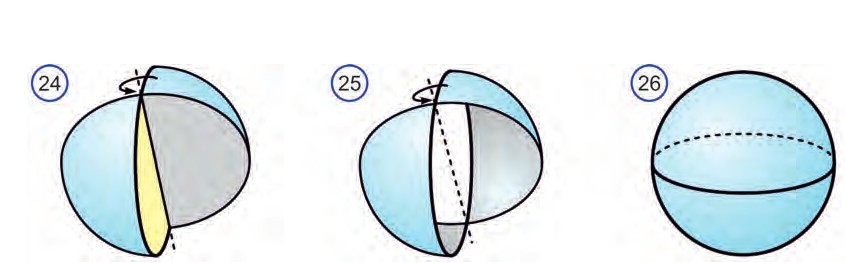
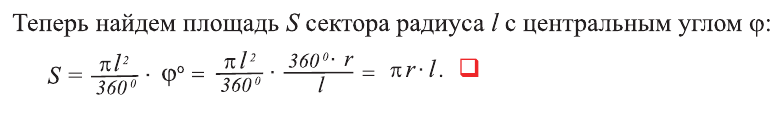Тело, полученное вращением круга вокруг своего диаметра, называют шаром (рис. 24). Поверхность, полученную при этом вращении, называют сферой. На рисунках 25 и 26 изображена сфера.

Формулы площадей боковой и полной поверхностей тел вращения:

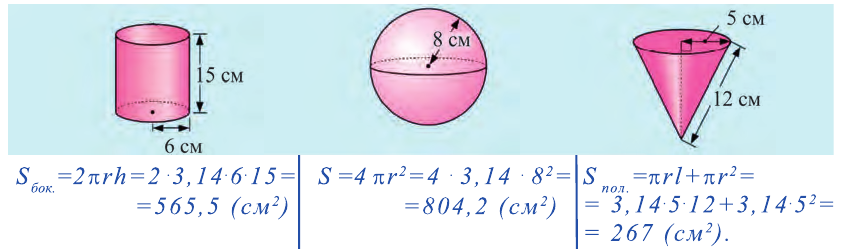
Пример:

Найдите площади боковых поверхностей следующих тел.

Решение: