
Техника дифференцирования с примерами решения
Вы уже умеете вычислять производные некоторых элементарных функций, пользуясь формулами: 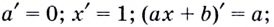
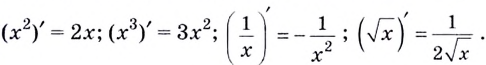
В этом параграфе будут рассмотрены теоремы, которые помогут находить производные сложных функций. Для упрощения записей вместо  будем писать
будем писать 
Теорема (о производной суммы). Если функции 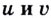 дифференцируемы в точке
дифференцируемы в точке 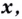 то в этой точке
то в этой точке 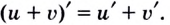
Доказательство. Найдём приращение 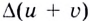 суммы данных функций на промежутке
суммы данных функций на промежутке 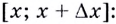
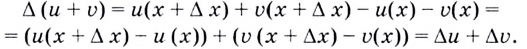
Поэтому
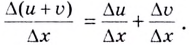
Если 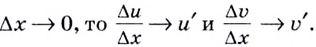 Следовательно,
Следовательно, 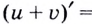
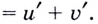
Аналогично можно доказать, что 
Теорема верна также для трёх и более функций. Например,
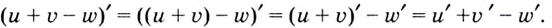
Теорема (о производной произведения). Если функции 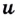 и
и 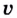 дифференцируемы в точке
дифференцируемы в точке 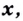 то
то
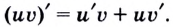
Доказательство. Найдём приращение 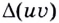 произведения данных функций на промежутке
произведения данных функций на промежутке 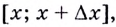 учитывая, что
учитывая, что
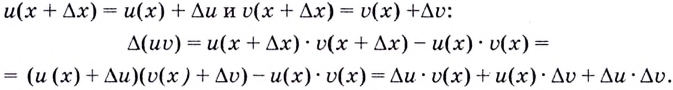
Поэтому
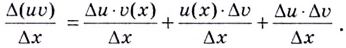
Если 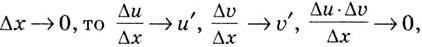 так как
так как 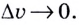
Следовательно,
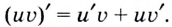
Следствие. Постоянный множитель можно выносить за знак производной. Ведь если 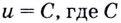 — постоянный множитель, то
— постоянный множитель, то 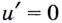 и по теореме о производной произведения
и по теореме о производной произведения 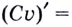
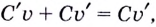 т.е.
т.е.
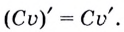
Теорема (о производной частного). Если 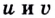 — функции от
— функции от 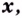 дифференцируемы в точке
дифференцируемы в точке 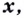 причём в этой точке
причём в этой точке 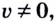 то
то
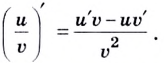
Доказательство теоремы можно провести аналогично двум предыдущим. А саму формулу производной частного можно вывести проще.
Пусть 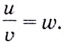 Тогда
Тогда 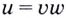 и по теореме о производной произведения
и по теореме о производной произведения 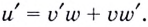 Выразим отсюда
Выразим отсюда 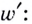
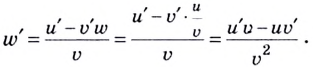
Итак:
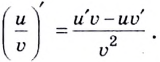
Теорема (о производной степени). Если 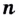 — число натуральное, то
— число натуральное, то
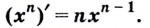
Доказательство. Докажем формулу 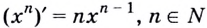 методом математической индукции.
методом математической индукции.
1. Проверим истинность равенства при 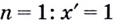 (равенство правильное).
(равенство правильное).
2. Предположим, что данное равенство выполняется при 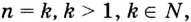 то есть равенство
то есть равенство 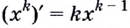 —истинно.
—истинно.
3. Докажем истинность равенства при 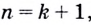 т. е. докажем равенство
т. е. докажем равенство 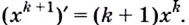
Рассмотрим левую часть и применим к ней теорему о производной произведения 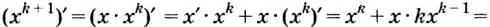
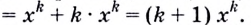
Следовательно, 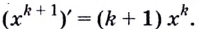
4. По принципу математической индукции данное равенство справедливо для произвольного натурального числа 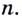
Позже будет показано, что эта формула верна не только для натуральных значений 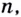 но и для любых действительных.
но и для любых действительных.
Примеры:
1. Если 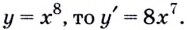
2. Если 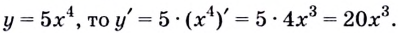
3. Если 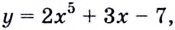 то по теореме о производной суммы
то по теореме о производной суммы 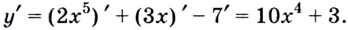
4. Если 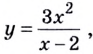 то по теореме о производной дроби
то по теореме о производной дроби
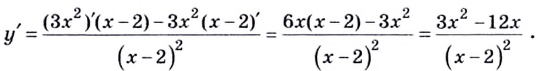
Из доказанных теорем следует, что каждая функция 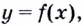 где
где 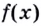 — многочлен, дифференцируема на всем множестве
— многочлен, дифференцируема на всем множестве 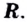 Поэтому каждый график такой функции — линия без разрывов и изломов. Если бы график функции в какой-то точке имел разрыв или перелом, то в этой точке функция не имела бы производной, то есть не была бы дифференцируемой. Дробно-рациональная функция от
Поэтому каждый график такой функции — линия без разрывов и изломов. Если бы график функции в какой-то точке имел разрыв или перелом, то в этой точке функция не имела бы производной, то есть не была бы дифференцируемой. Дробно-рациональная функция от 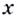 дифференцируема в каждой точке
дифференцируема в каждой точке 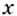 её области определения.
её области определения.
Пример:
Найдите производную функции 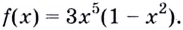
Решение:
Способ 1. Воспользуемся теоремой о производной произведения:
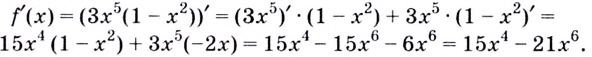
Способ 2. Сначала раскроем скобки, а затем применим теорему о производной суммы.
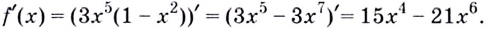
Пример:
Вычислите значение производной функции 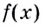 в точке
в точке
Решение:
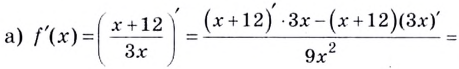
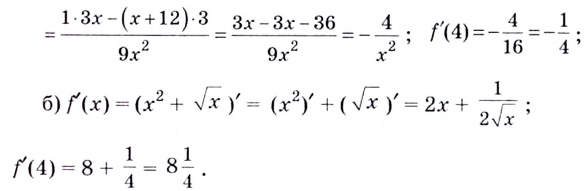
Пример:
Запишите уравнение касательной к графику функции 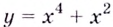 в точке
в точке 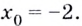
Решение:
Уравнение касательной имеет вид:
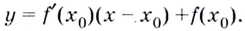
Найдем: 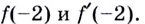
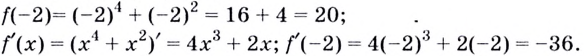
Следовательно: 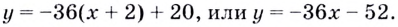
| Рекомендую подробно изучить предметы: |
| Ещё лекции с примерами решения и объяснением: |