Свойство точек биссектрисы угла - определение и вычисление с доказательствами и примерами решения

Свойство точек биссектрисы угла:

По определению биссектриса угла делит угол пополам.

У биссектрисы есть еще одно важное свойство.

Теорема (о биссектрисе угла).

Любая точка биссектрисы угла равноудалена от сторон угла. Если точка внутри угла равноудалена от сторон угла, то она лежит на биссектрисе этого угла.

В данной теореме два утверждения: прямое и ему обратное. Докажем каждое из этих утверждений отдельно.

1) Дано: AD — биссектриса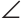

Доказать: MK=MN.

Доказательство:

Прямоугольные треугольники АКМ и ANM равны по гипотенузе и острому углу (гипотенуза AM — общая, KAM =NAM, так как AD — биссектриса). Катеты МК и MN равны как соответствующие в двух равных треугольниках.

2) Дано: 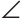BAC, МК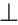AB, MN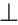AC, МК = MN, M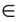AD (рис. 272).

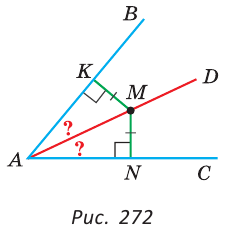
Доказать: луч AD — биссектриса BAC.

Доказательство:

Прямоугольные треугольники АКМ и ANM равны по катету и гипотенузе (гипотенуза AM — общая, МК = MN по условию). Углы КAM и NAM равны как соответствующие в двух равных треугольниках, откуда луч AD — биссектриса BAC. Теорема доказана.

Из доказанной теоремы следует, что биссектриса является геометрическим местом точек плоскости, находящихся внутри угла и равноудаленных от сторон угла.

Пример:

В прямоугольном треугольнике ABC C = 90°, 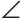A = 40° (рис. 273). На катете АС взята точка К так, что КС=6 см и KBC = 25°. Найти расстояние от точки К до прямой АВ.

Решение:

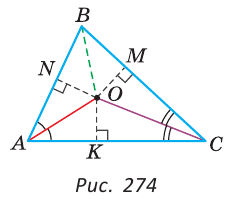
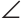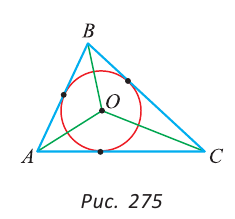
Искомое расстояние равно длине перпендикуляра КМ к прямой АВ. Так как ABC = 90° -A = 90° - 40° = 50°, то 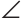ABK = 50° - 25° = 25°. Следовательно, ВК — биссектриса угла ABC. Поскольку любая точка биссектрисы угла равноудалена от сторон угла, то КМ = КС = 6 см.

Ответ: 6 см.

Пример: (2-я замечательная точка треугольника).

Доказать, что биссектрисы треугольника пересекаются в одной точке.

Доказательство:

Проведем в АВС биссектрисы углов А и С. Пусть О — точка их пересечения (рис. 274).

Так как точка О лежит на биссектрисе АО угла А, то она равноудалена от сторон угла А, то есть равны перпендикуляры ON и ОК к сторонам угла А. Так как точка О лежит на биссектрисе СО угла С, она равноудалена от сторон угла С, то есть равны перпендикуляры ОК и ОМ к сторонам угла С. Тогда ОК = ОМ = ON. Так как перпендикуляры ON и ОМ равны, то точка О равноудалена от сторон угла В. Точка, равноудаленная от сторон угла, лежит на биссектрисе этого угла. Поэтому биссектриса угла В пройдет через точку О, и, следовательно, все три биссектрисы пересекутся в одной точке.

Замечание. Точка пересечения биссектрис треугольника является центром вписанной в него окружности (рис. 275), которая касается всех трех сторон треугольника (имеет с каждой из сторон только одну общую точку).

Пример:

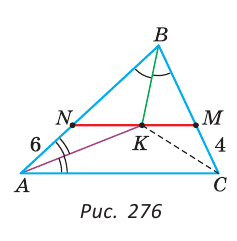
В треугольнике ABC биссектрисы углов А и В пересекаются в точке К. Через точку К проведен отрезок NM, параллельный стороне АС с концами на сторонах АВ и ВС соответственно; AN = 6 см, МС = 4 см. Найти отрезок NM.

Решение:

Так как биссектрисы треугольника пересекаются в одной точке, то СК — биссектриса угла С (рис. 276).

Треугольник ANK — равнобедренный. Действительно, 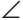NAK =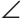CAK, поскольку АК — биссектриса, 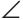CAK =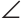AKN как накрест лежащие при параллельных прямых NM и АС и секущей АК, откуда 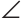NAK =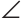AKN и треугольник ANК —  равнобедренный по признаку равнобедренного треугольника. Тогда NK=AN=6 см. Аналогично доказываем, что треугольник KMC — равнобедренный и КМ=МС=4 см.

Искомый отрезок NM = NK + КМ = 6 + 4=10 (см).

Ответ: 10 см.

Замечание. Решив задачу 3, мы доказали, что если NM || АС и отрезок NM проходит через точку пересечения биссектрис, то периметр NBM равен АВ+ВС.