Свойство катета прямоугольного треугольника, лежащего против угла в 30° с примерами

Свойство катета прямоугольного треугольника, лежащего против угла в 30°:

Теорема (о катете, лежащем против угла в 30°). Катет прямоугольного треугольника, лежащий против угла в 30°, равен половине гипотенузы.

Дано:

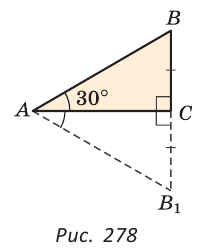
Доказать: ВС = 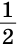АВ.

Доказательство:

На луче ВС отложим отрезок СВ₁ равный отрезку ВС. Так как            АВ₁С =АВС по двум катетам (катет АС — общий), то 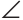B₁AC =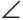BAC = 30°,

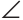BAB₁ = 60°. Но 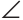В = 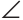В₁ = 60°. Известно, что если у треугольника все углы равны, то он равносторонний. Отсюда АВВ₁ — равносторонний, АВ = ВВ₁, ВС = 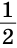ВВ₁ =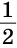АВ. Теорема доказана.

Верно и утверждение, обратное данному. Докажем его.

Теорема. Если в прямоугольном треугольнике катет равен половине гипотенузы, то этот катет лежит против угла в 30°.

Доказательство:

Пусть в треугольнике ABC 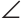C = 90°, АВ = 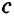, ВС=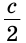 (рис. 279).

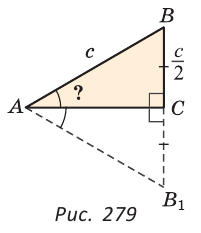
Докажем, что BAC = 30°. Продлим катет ВС на его длину: СВ₁ = ВС. Из равенства прямоугольных треугольников АСВ₁ и АСВ (по двум катетам) следует, что АВ₁ = АВ = ВВ₁ = 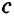. Значит, АВВ₁ — равносторонний, все его углы равны по 60°, а его высота АС является биссектрисой. Поэтому BAC = 30°. Что и требовалось доказать.

Пример:

В прямоугольном треугольнике ABC, у которого C = 90°, A=30°, проведена высота CD. Найти отрезок AD, если BD = 8 см.

Решение:

Так как угол А и угол BCD дополняют угол В до 90°, то BCD=A=30° (рис. 280).

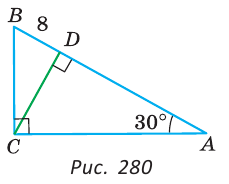
В прямоугольном треугольнике CDB катет BD лежит против угла в 30°.  Поэтому СВ = 2BD = 16 см.

В треугольнике ABC катет ВС лежит против угла в 30°. Поэтому АВ = 2ВС = 32 см.

Отсюда AD=AB-BD = 32 - 8 = 24 (см).

Ответ: 24 см.

Замечание. Мы доказали, что BC = 2BD, AB = 2BC = 4BD, AD = АВ - BD = 3BD, то есть в прямоугольном треугольнике с углом 30° высота делит гипотенузу в отношении 1 : 3.

Пример:

Дан прямоугольный треугольник с углом 15°. Высота, проведенная к гипотенузе, равна 2 см. Найти гипотенузу.

Решение:

Пусть в треугольнике ABC ACB = 90°, 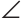B = 15°, СН = 2 см — высота (рис. 281).

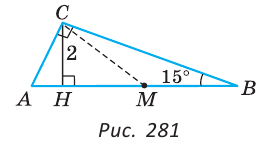
Нужно найти АВ. Проведем медиану СМ треугольника ABC. Так как в прямоугольном треугольнике медиана, проведенная к гипотенузе, равна половине гипотенузы, то СМ = MB. Треугольник СМВ — равнобедренный, MCB = CBM = 15°, AMC — его внешний угол.

По свойству внешнего угла AMC =MCB +MBC = 15° + 15° = 30°.

В прямоугольном треугольнике СНМ катет СН лежит против угла в 30°, поэтому он равен половине гипотенузы СМ. Отсюда СМ = 2СН = 4 см, АВ = 2СМ = 8 см.

Ответ: 8 см.