
Свойства внутренних сил системы в теоретической механике
Свойства внутренних сил системы:
Механической системой называется любая совокупность материальных точек.
Внешними силами механической системы называются силы, с которыми действуют на точки системы тела и точки, не входящие в рассматриваемую систему.
Внутренними силами механической системы называют силы взаимодействия между точками рассматриваемой системы.
Внешнюю силу, приложенную к какой-либо точке системы, обозначим 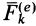
Рассмотрим некоторые простейшие свойства внутренних сил, действующих на всю механическую систему в любом ее состоянии. Докажем, что главный вектор всех внутренних сил системы и главный момент этих сил относительно произвольной точки равны нулю при любом состоянии системы, т. е. при ее равновесии и при произвольном движении.
Пусть система состоит из 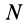 —любое конечное число (рис. 38). Условимся пределы у суммы не ставить, когда суммирование производится по всем
—любое конечное число (рис. 38). Условимся пределы у суммы не ставить, когда суммирование производится по всем 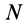 точкам системы. Если рассмотреть какие-либо две произвольные точки системы, например
точкам системы. Если рассмотреть какие-либо две произвольные точки системы, например 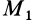 и
и 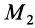 , то для них
, то для них 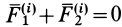 , так как силы действия и противодействия всегда равны друг другу по модулю, противоположны по направлению и действуют вдоль одной прямой линии, соединяющей взаимодействующие точки. Главный вектор внутренних сил
, так как силы действия и противодействия всегда равны друг другу по модулю, противоположны по направлению и действуют вдоль одной прямой линии, соединяющей взаимодействующие точки. Главный вектор внутренних сил 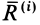 состоит из векторной суммы таких сил действия и противодействия, так как вся система состоит из пар взаимодействующих точек. Следовательно,
состоит из векторной суммы таких сил действия и противодействия, так как вся система состоит из пар взаимодействующих точек. Следовательно,

В проекциях на координатные оси
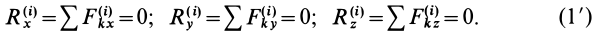
Внешние силы тоже являются силами взаимодействия, но для них силы действия приложены к точкам рассматриваемой системы, а силы противодействия приложены к телам и точкам, не входящим в эту систему.
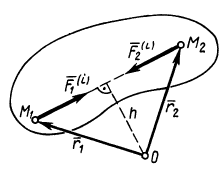
Рис. 38
Рассмотрим теперь сумму моментов сил 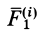 и
и 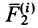 относительно точки
относительно точки 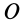 . Легко видеть, что
. Легко видеть, что
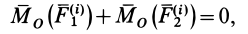
так как обе силы имеют одинаковые плечи и противоположные направления векторных моментов. Главный момент внутренних сил 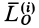 относительно точки
относительно точки  состоит из векторной суммы таких выражений, равных нулю. Следовательно,
состоит из векторной суммы таких выражений, равных нулю. Следовательно,
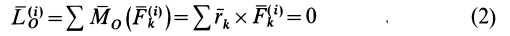
и соответственно в проекциях на координатные оси
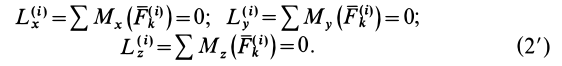
| Рекомендую подробно изучить предмет: |
| Ещё лекции с примерами решения и объяснением: |
- Дифференциальное уравнение движения системы
- Теоремы об изменении количества движения и о движении центра масс
- Теорема об изменении кинетического момента
- Теорема об изменении кинетической энергии
- Криволинейное движение материальной точки
- Движение несвободной материальной точки
- Относительное движение материальной точки
- Геометрия масс