
Свойства вероятности - определение и вычисление с примерами решения
Содержание:
Основные свойства вероятности:
Сразу же отметим, что рассматривая основные свойства вероятности, будем говорить лишь о таких событиях, для определения вероятностей которых можно построить полную систему событий с конечным числом исходов.
Первые два свойства очевидны:
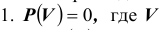
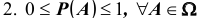
Эти свойства нетрудно доказать. Например, то что 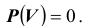 Действительно так как
Действительно так как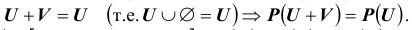 Но согласно III-ей аксиоме
Но согласно III-ей аксиоме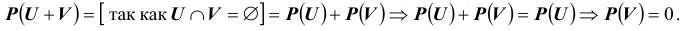
Замечание 1. Если вероятность события равна нулю (единице), то это еще не означает, что событие невозможное (достоверное). Это означает только то, что при неограниченном увеличении числа опытов частота появления этого события будет стремиться к нулю (единице).
Сформулируем и докажем еще несколько свойств. А именно:
3. Если 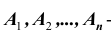 полная группа попарно несовместных событий, то
полная группа попарно несовместных событий, то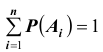
Действительно, из определения полной группы (системы) событий следует, что
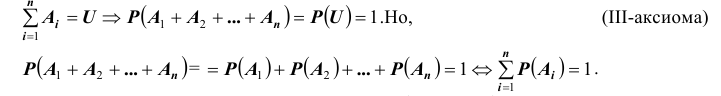
4. Если событие A влечет за собой событие 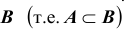 ,то вероятность события
,то вероятность события
A не может превышать вероятность события B , т.е. 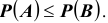
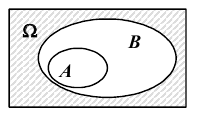
Доказательство 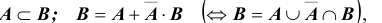 причем
причем 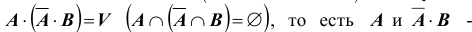 несовместны. Следовательно,согласно III - ей аксиоме:
несовместны. Следовательно,согласно III - ей аксиоме: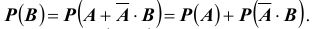 Но, по I-ой аксиоме
Но, по I-ой аксиоме 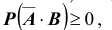 так как вероятность любого
так как вероятность любого
события неотрицательна. Значит 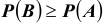 что и требовалось доказать.
что и требовалось доказать.
Замечание 2. Выше, при доказательстве свойств использовалось аксиоматическое определение вероятности. Нетрудно доказать, например теорему сложения вероятностей несовместных событий, используя классическое определение вероятности.
ТЕОРЕМА (сложения вероятностей несовместных событий): Если
события A и B несовместны,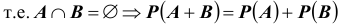
Доказательство. Пусть полная система состоит из n исходов. Пронумеруем её случаи так, чтобы первые m случаев 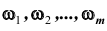 благоприятствовали событию A, но не B, тогда
благоприятствовали событию A, но не B, тогда 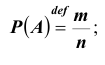 следующие l случаев
следующие l случаев 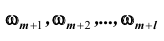 благоприятствовали событию B , но не A, тогда
благоприятствовали событию B , но не A, тогда 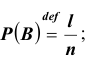 а остальные случаи
а остальные случаи
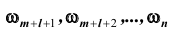 не благоприятствовали ни событию A, ни событию B . В силу несовместности указанных событий A и B , благоприятствующих исходов и событию A и событию B одновременно в полной системе
не благоприятствовали ни событию A, ни событию B . В силу несовместности указанных событий A и B , благоприятствующих исходов и событию A и событию B одновременно в полной системе нет.
нет.
Итак:
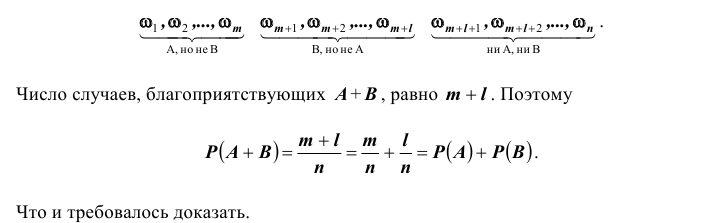
Пример:
В урне 100 шаров, из них 20 белых (не цветных), 30 синих и 50 красных. Какова вероятность появления цветного шара?
Решение. Пусть событие A - появление белого шара 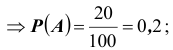 событие B - появление синего шара
событие B - появление синего шара 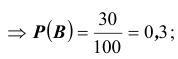 событие C - появление красного шара
событие C - появление красного шара 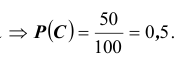
Найдем 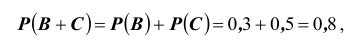 или
или 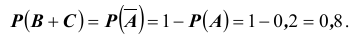
Замечание 3. Для несчетного случая исходов, составляющих 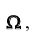 , теорема сложения несовместных событий принимается в качестве одной из основных аксиом теории вероятностей:
, теорема сложения несовместных событий принимается в качестве одной из основных аксиом теории вероятностей: 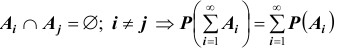 Заметим также, что если
Заметим также, что если 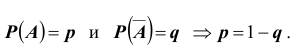
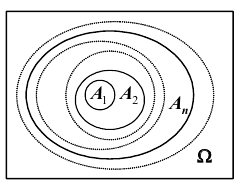
Будем говорить, что последовательность событий 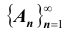 монотонно возрастает (см. рис.), если
монотонно возрастает (см. рис.), если 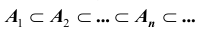 Тогда
Тогда 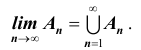
Аналогично, последовательность событий 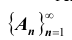 монотонно убывает, если
монотонно убывает, если 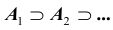
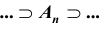
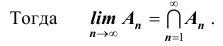
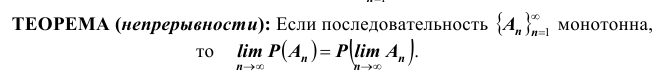
Условная вероятность и независимость событий
Итак, ране нами было введено понятие вероятности как числовой функции, удовлетворяющей трём основным аксиомам. Такую вероятность называют безусловной, подчеркивая этим, что она не зависит ни от каких дополнительных условий, кроме фиксированного комплекса условий S , которым характеризуется данный конкретный эксперимент.
Определение. Пусть A и B - наблюдаемые события при выполнении условий S , причем 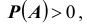 тогда вероятность события B , вычисленная в предположении, что произошло событие A, называется условной вероятностью события B (обозначается
тогда вероятность события B , вычисленная в предположении, что произошло событие A, называется условной вероятностью события B (обозначается 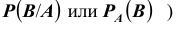 и определяется равенством
и определяется равенством
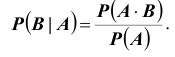
Для краткости условную вероятность 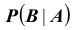 называют «вероятностью события B при условии A». Заметим, что при
называют «вероятностью события B при условии A». Заметим, что при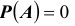 условная вероятность
условная вероятность 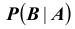 не определена.
не определена.
Пример:
В урне 8 белых и 2 красных шара. Событие A- появление белого шара. Очевидно, что до испытания (вынимание шаров) 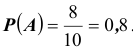 Вынут один шар (шар в урну не возвращается). Этот шар оказался белым. Следовательно, во втором испытанием
Вынут один шар (шар в урну не возвращается). Этот шар оказался белым. Следовательно, во втором испытанием 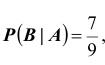 где событие B - появление белого шара во втором испытании.
где событие B - появление белого шара во втором испытании.
ТЕОРЕМА (умножения вероятностей): Вероятность произведения любых
двух событий A и B вычисляется по формуле:
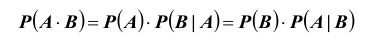
Доказательство. Это утверждение непосредственно следует из определения условной вероятности.
Если пронумеровать случаи полной системы событий 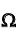 так, что
так, что
то по определению 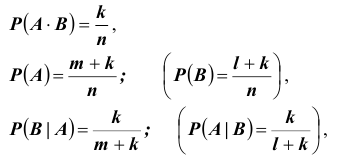 поэтому
поэтому 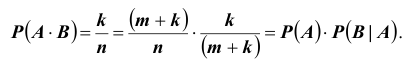 аналогично
аналогично 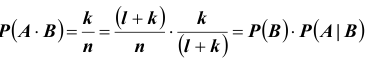 Что и требовалось доказать.
Что и требовалось доказать.
Замечание. Для случая трех событий теорема умножения вероятностей имеет
вид:
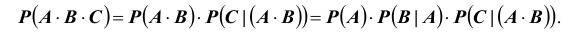
Пример:
Каждая буква слова «лотос» написана на отдельной карточке. Какова вероятность того, что наугад извлеченные одна за другой три карточки составят слово «сто»?
Решение. Пусть 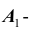 - событие, состоящее в том, что на первой карточке написана буква «С»;
- событие, состоящее в том, что на первой карточке написана буква «С»; 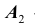 - на второй карточке буква «Т»;
- на второй карточке буква «Т»; 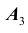 - на третьей карточке буква «О» и пусть A- событие, состоящее в том, что получилось слово «СТО». Нетрудно видеть, что
- на третьей карточке буква «О» и пусть A- событие, состоящее в том, что получилось слово «СТО». Нетрудно видеть, что 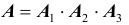
Далее 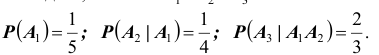 тогда по теореме получаем
тогда по теореме получаем 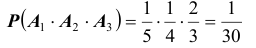
Определение 1: Событие A называется независимым от события B , удовлетворяющего условию 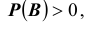 , если выполняется
, если выполняется
равенство 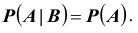
Определение 2: События A и B называются независимыми, если 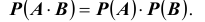 .
.
Определение 3: События 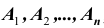 называются независимыми в совокупности, если для любого набора из m событий
называются независимыми в совокупности, если для любого набора из m событий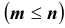 (т.е. для любого набора индексов
(т.е. для любого набора индексов 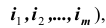 , которые попарно независимы, справедливо равенство:
, которые попарно независимы, справедливо равенство:
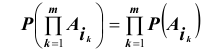
Важно здесь отметить то, что из попарной независимости ещё не следует независимость в совокупности. Рассмотрим пример.
Пример: (Бернштейна).
Имеем правильный тетраэдр, грани которого
окрашены следующим образом:
- красным цветом (появление этого цвета - событие A);
- синим цветом (появление этого цвета - событие B );
- зелёным цветом (появление этого цвета - событие C ;
- полосы красного, синего и зеленого цветов.
Вычислим: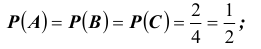
1.1. Проверим, являются ли события A,B,C попарно независимыми.
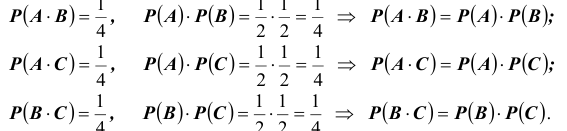
Вывод: события A,B,C - попарно независимы.
2. Проверим их независимость в совокупности.
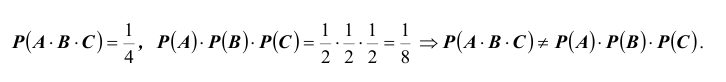
Следовательно, как видим, попарной независимости недостаточно для независимости в совокупности.
ТЕОРЕМА (сложения вероятностей совместных событий): Если события A и B совместны, т.е.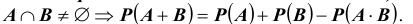
Другими словами : Вероятность суммы совместных событий A и B равна сумме вероятностей этих событий минус вероятность их произведения.
Доказательство. Доказательство проведем, использую геометрический метод. Итак, запишем очевидные соотношения:

Пример:
Вероятность попадания в мишень первым стрелком равна 0,8; для второго стрелка эта вероятность равна 0,6. Стрелки независимо друг от друга произвели по одному выстрелу. Какова вероятность того, что в мишень попадет хотя бы один стрелок?
Решение. Пусть
A- событие, состоящее в том, что мишень поражена первым стрелком;
B - мишень поражена вторым стрелком;
C - мишень поражена хотя бы одним стрелком (т.е. - или первым, или вторым, или обоими стрелками одновременно). Очевидно, что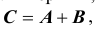 причем, A,B - совместны (возможно их совместное появление).
причем, A,B - совместны (возможно их совместное появление).
Тогда:
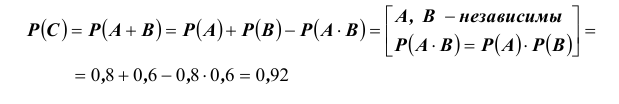
Следствие 1.
Если события A и B независимы 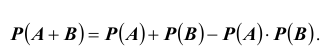
Следствие 2.
Если события A и B несовместны 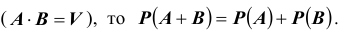
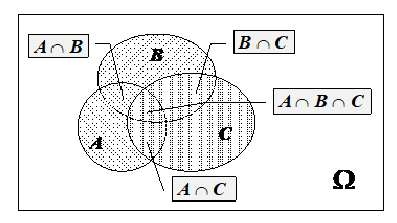
Замечание. Из геометрических соображений (см. рис.) очевидно, что: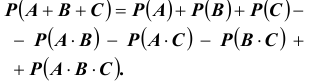
Решение примеров на свойства вероятности
Пример:
В ящике 2 диода и 8 транзисторов. Какова вероятность того, что вынимая не глядя два раза подряд по одной детали, мы оба раза достанем транзисторы?
Решение.
Введем: событие 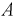 - из ящика первый раз достали транзистор, событие
- из ящика первый раз достали транзистор, событие 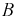 - из ящика второй раз достали транзистор. Тогда вероятность события
- из ящика второй раз достали транзистор. Тогда вероятность события 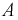 определяется так:
определяется так: 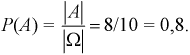 Условная вероятность события
Условная вероятность события 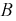 при условии, что произошли событии
при условии, что произошли событии 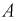 (здесь благоприятствующих событий будет
(здесь благоприятствующих событий будет 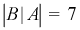 и приведенное пространство элементарных событий
и приведенное пространство элементарных событий 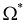 будет состоять
будет состоять 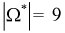 событий. Тогда условную вероятность события
событий. Тогда условную вероятность события 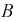 при условии, что событие
при условии, что событие 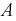 произошло найдем так:
произошло найдем так: 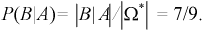
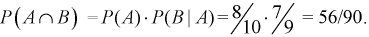
Пример:
Составлена схема электрической цепи (рис. 1.13).
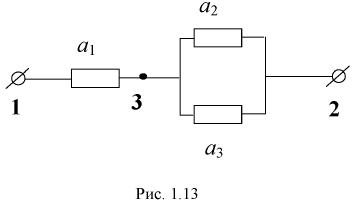
Заданы вероятности работы элементов схемы 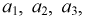 соответственно
соответственно 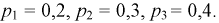 Найти вероятность того, что ток пройдет с клеммы 1 на клемму 2.
Найти вероятность того, что ток пройдет с клеммы 1 на клемму 2.
Решение.
Введем события: 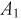 - работает элемент
- работает элемент 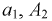 - работает элемент
- работает элемент 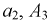 работает элемент
работает элемент 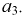 Тогда
Тогда 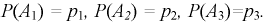 Введем в схему точку 3, которая разбивает схему на два последовательно соединенных участка, через которые проходит ток - от точки 1 до точки 3 и от точки 3 до точки 2. Рассмотрим событие
Введем в схему точку 3, которая разбивает схему на два последовательно соединенных участка, через которые проходит ток - от точки 1 до точки 3 и от точки 3 до точки 2. Рассмотрим событие 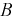 - ток пройдет из точки 1 в точку 3 схемы. Поскольку между точками 1 и 3 включен только один элемент
- ток пройдет из точки 1 в точку 3 схемы. Поскольку между точками 1 и 3 включен только один элемент 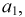 то событие
то событие 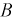 выполнится тогда, когда будет работать элемент
выполнится тогда, когда будет работать элемент 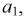 значит
значит 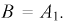 Введем событие
Введем событие 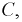 состоящее в том, что ток пройдет из точки 3 в точку 2. Оно выполнится тогда, когда будет работать или элемент
состоящее в том, что ток пройдет из точки 3 в точку 2. Оно выполнится тогда, когда будет работать или элемент 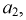 или
или 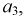 или
или 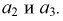 Мы видим, что для описания события
Мы видим, что для описания события 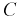 надо использовать теоремы о сумме или объединении двух произвольных событий
надо использовать теоремы о сумме или объединении двух произвольных событий 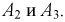 Запишем
Запишем 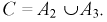
Теперь рассмотрим событие 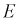 ток пройдет из точки 1 в точку 2. Оно выполнится тогда, когда выполнится и событие
ток пройдет из точки 1 в точку 2. Оно выполнится тогда, когда выполнится и событие 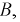 и событие
и событие 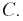 Здесь надо использовать теоремы об умножении или пересечении двух событий, запишем
Здесь надо использовать теоремы об умножении или пересечении двух событий, запишем 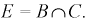 Тогда вероятность события
Тогда вероятность события 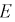 определяется по формуле (1.9), а с учетом того, что события
определяется по формуле (1.9), а с учетом того, что события 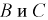 независимы применяем формулу (1.13):
независимы применяем формулу (1.13):
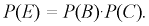
Найдем 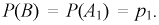 Определим
Определим 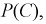 применяя теорему о вероятности суммы двух произвольных событий (т. к. события
применяя теорему о вероятности суммы двух произвольных событий (т. к. события 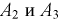 могут происходить совместно) и используя формулы (1.4) или (1.6):
могут происходить совместно) и используя формулы (1.4) или (1.6):
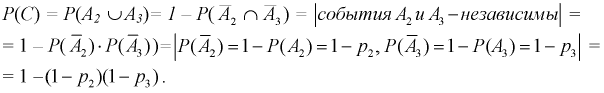
Тогда вероятность того, что ток пройдет из точки 1 в точку 2
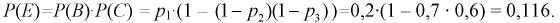
| Рекомендую подробно изучить предметы: |
| Ещё лекции с примерами решения и объяснением: |