Свойства прямоугольного треугольника - определение и вычисление с примерами решения

Свойства прямоугольного треугольника:

Рассмотрим свойства прямоугольного треугольника, которые следуют из теоремы о сумме градусных мер углов треугольника.

Свойство 1 (свойство катета, лежащего против угла в 30°). Катет прямоугольного треугольника, лежащий против угла в 30°, равен половине гипотенузы.

Доказательство.

1) Пусть АСВ — прямоугольный треугольник, в котором

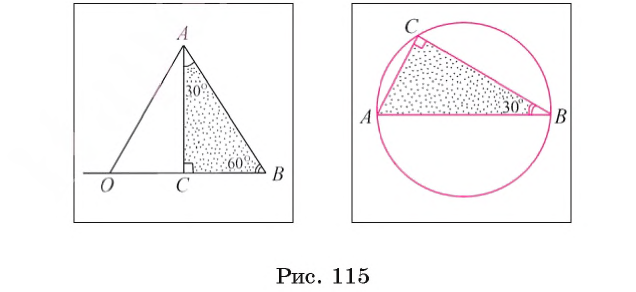
2) Так как сумма градусных мер углов треугольника равна 180°, то в прямоугольном треугольнике АСВ ABC = 60°.
3) Пусть точка О лежит на луче ВС так, что СО = СВ. Тогда прямоугольные треугольники АСО и АСВ равны по двум катетам (катет АС — общий, СО = СВ), следовательно, AOB = 60°.

4) В треугольнике АОВ выполняются равенства AOB = OAB = 60°, а, значит, стороны, лежащие против этих углов, равны, т. е. АВ = ОВ. Так как CB =  OB, следовательно, CB =  AB.

Свойство доказано.

Например, пусть отрезок АВ — диаметр окружности, а точка С принадлежит окружности и ABC = 30°, тогда AC =  AB. Действительно, в треугольнике АСВ угол С прямой (см. задачу 251, § 1, глава 5). Тогда в прямоугольном треугольнике АСВ катет АС равен половине гипотенузы АВ, т. е. AC =  AB (рис. 115, б).

Свойство 2. Если катет прямоугольного треугольника равен половине гипотенузы, то градусная мера угла, лежащего против этого катета, равна 30°.

Доказательство.

1) Пусть в прямоугольном треугольнике АСВ катет ВС равен половине гипотенузы АВ. Докажем, что градусная мера угла CAB равна 30° (рис. 116).

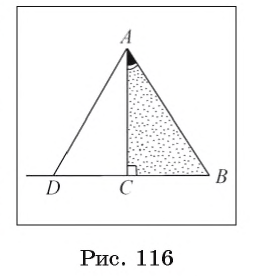
2) Пусть точка D лежит на луче ВС так, что CD = СВ. Тогда треугольники АСВ и ACD равны по двум катетам. Отсюда следует, что АD = АВ, а поскольку DВ = 2 СВ = АВ, то треугольник АDВ равносторонний и градусная мера каждого его угла равна 60°. Так как DAB = 2CAB = 60°, то САВ = 30°.

Свойство доказано.

Пример:

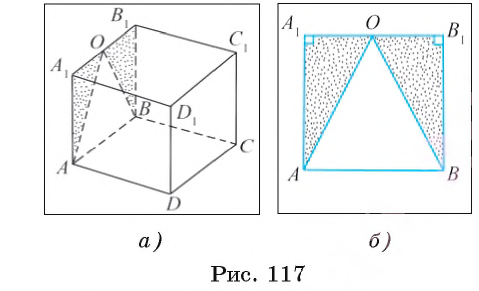
Точка О — середина ребра А₁В₁ куба АВСDА₁В₁С₁D₁. Докажите, что треугольник АОВ — равнобедренный (рис. 117, а).

Дано:

АВСDА₁В₁С₁D₁— куб,

О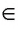А₁В₁, А₁О = ОВ₁.

Доказать: А ОВ — равнобедрен ный.

Доказательство.

Для доказательства равенства каких-либо отрезков достаточно доказать равенство некоторых треугольников, сторонами которых являются эти отрезки.

1) Рассмотрим треугольники АА₁О и ВВ₁О (см. рис. 117, а). Так как гранями куба служат квадраты, то AA₁O = BB₁O = 90°, т. е. треугольники АА₁О и ВВ₁О — прямоугольные.

2) Докажем равенство прямоугольных треугольников АА₁О и ВВ₁О . Поскольку стороны квадрата равны, то АА₁ = ВВ₁ (см. рис. 117, а, б). Кроме того, по условию А₁О = ОВ₁. Таким образом, прямоугольные треугольники АА₁О и ВВ₁О равны по двум катетам. Из равенства этих треугольников следует, что АО = ОВ, т. е. треугольник АОВ — равнобедренный.

Справочный материал:

Признаки равенства прямоугольных треугольников

• ✓ Признак равенства прямоугольных треугольников по гипотенузе и катету. Если гипотенуза и катет одного прямоугольного треугольника соответственно равны гипотенузе и катету другого, то такие треугольники равны.
• ✓ Признак равенства прямоугольных треугольников по двум катетам. Если катеты одного прямоугольного треугольника соответственно равны катетам другого, то такие треугольники равны.
• ✓ Признак равенства прямоугольных треугольников по катету и прилежащему острому углу. Если катет и прилежащий к нему острый угол одного прямоугольного треугольника соответственно равны катету и прилежащему к нему острому углу другого, то такие треугольники равны.
• ✓ Признак равенства прямоугольных треугольников по катету и противолежащему острому углу. Если катет и противолежащий ему острый угол одного прямоугольного треугольника соответственно равны катету и противолежащему ему острому углу другого, то такие треугольники равны.
• ✓ Признак равенства прямоугольных треугольников по гипотенузе и острому углу. Если гипотенуза и острый угол одного прямоугольного треугольника соответственно равны гипотенузе и острому углу другого, то такие треугольники равны.

Свойства прямоугольного треугольника

• ✓ В прямоугольном треугольнике гипотенуза больше катета. Катет, лежащий против угла, величина которого равна 30°, равен половине гипотенузы.
• ✓ Если катет равен половине гипотенузы, то угол, лежащий против этого катета, равен 30°.