Свойства и график функции y=n x (n>1, n∈N) с примерами решения

Содержание:

Зависимость, при которой каждому неотрицательному числу ставится в соответствие значение корня заданной четной степени, задает функцию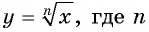

Действительно, по свойствам арифметического корня существует единственный арифметический корень четной степени из неотрицательного числа, значит, каждому неотрицательному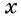

При 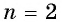 функция принимает вид  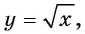свойства которой рассматривались в 8-м классе.

Для любого действительного числа существует единственный корень нечетной степени (по свойствам корня нечетной степени).

Рассмотрим свойства функции 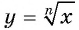 для четных и нечетных показателей корня.

Функция y=^2k√x, где K∈N

Функция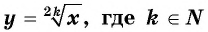 

1. Область определения функции. По свойству арифметического корня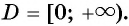 

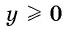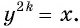2. Множество значений функции. Наибольшее и наименьшее значения функции. По определению арифметического корня из числа:  и  По свойству степени с натуральным показателем для любого  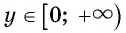существует значение  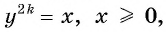т. е. множеством значений функции  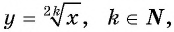является множество неотрицательных чисел: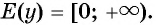 

При 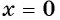 функция принимает наименьшее значение  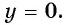Наибольшего значения у функции не существует.

3. Нули функции. Так как 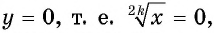 при 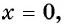 то значение  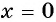является единственным нулем функции.

4. Промежутки знакопостоянства функции, 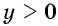 при всех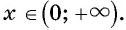 

5. Промежутки монотонности функции. Функция возрастает на всей области определения.

Действительно, если 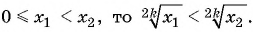 В противном случае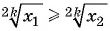 

или 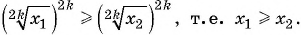 Противоречие доказывает утверждение.

6.Четность (нечетность) функции. Так как область определения функции не симметрична относительно начала координат, то функция не является четной и не является нечетной.

7. График функции. Графики функци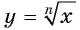й  при 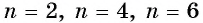 изображены на рисунке 120.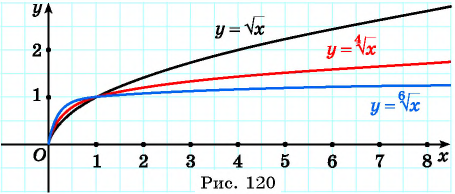

Функция y=^2k+1√x, где K∈N

Функция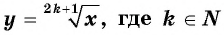   

1. Область определения функции. По свойству корня нечетной степени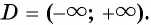   

2. Множество значений функции. Наибольшее и наименьшее значения функции. По определению корня 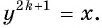 По свойству степени с натуральным показателем для любого  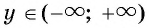существует  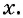Таким образом, множеством значений функции  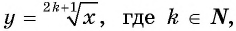является множество всех действительных чисел: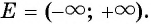 

Наибольшего и наименьшего значений у функции 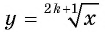 не существует.  

3. Нули функции. Так как 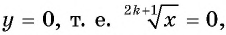 при 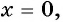 то значение  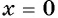является единственным нулем функции.  

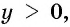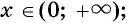
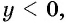4. Промежутки знакопостоянства функции,  если если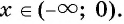   

5. Промежутки монотонности функции. Функция возрастает на всей области определения.

Если 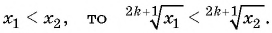 В противном случае  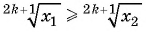или 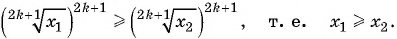  Противоречие доказывает утверждение.  

6. Четность (нечетность) функции. Так как область определения функции 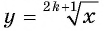 симметрична относительно начала координат и  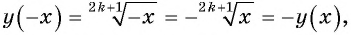то функция является нечетной. Ее график симметричен относительно начала координат.

7. График функции. Графики функци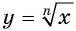й  при 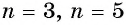 изображены на рисунке 121.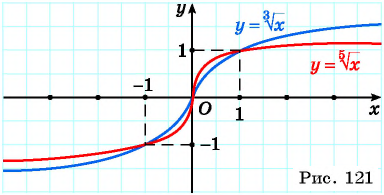  

Примеры заданий и их решения

Пример №1

Найдите область определения функции:

Решение:

а) Так как область определения корня четной степени есть множество неотрицательных чисел, то подкоренное выражение должно быть неотрицательным. Решим неравенство 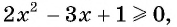 получим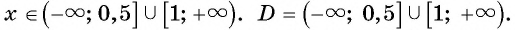 

б) Так как область определения корня нечетной степени есть множество всех действительных чисел, то подкоренное выражение может принимать любые значения при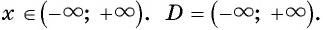 

Пример №2

Найдите множество значений функции:

Решение:

а) Множеством значений функции 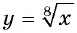 является промежуток  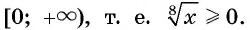По свойству неравенств: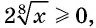 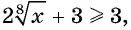 значит,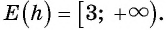 

б)Множеством значений функции 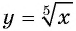 является множество всех действительных чисел  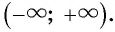  Значит, и множеством значений функции  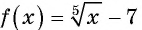является множество всех действительных чисел, т. е.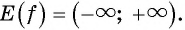 

Пример №3

Определите наименьшее значение функции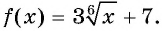 

Решение:

Так как функция 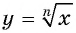 для четных  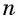имеет наименьшее значение, равное нулю, при  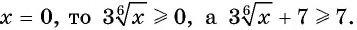Следовательно, наименьшее значение данной функции равно 7 и достигается при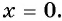 

Пример №4

Найдите нули функции:

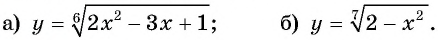
Решение:

а) Так как значение корня 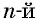 степени равно нулю, если его подкоренное выражение равно нулю, то решим уравнение  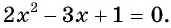Его корни  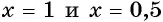являются нулями функции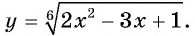 

б) Так как значение корня 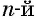 степени равно нулю, если его подкоренное выражение равно нулю, то решим уравнение  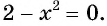Его корни  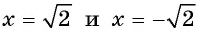являются нулями функции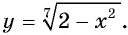 

• Заказать решение задач по высшей математике

Пример №5

Какие значения принимает функция на указанных промежутках:

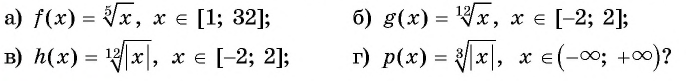
Решение:

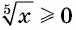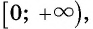а) Так как  для  то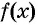 принимает положительные значения для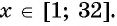 

б)Так как 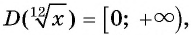 то функция  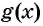не определена для отрицательных значений  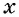из промежутка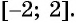 

в)Так как 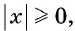 то функция  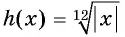принимает неотрицательные значения для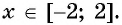 

г)Так как 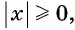 то функция  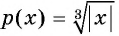принимает неотрицательные значения для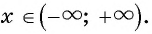 

Пример №6

Расположите числа 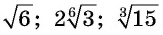 в порядке возрастания.

Решение:

Запишем числа 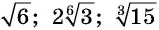 в виде корней с одинаковыми показателями:

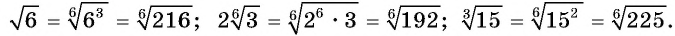
Поскольку функция 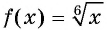 возрастает на промежутке  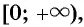то 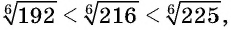 значит,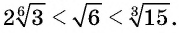 

Пример №7

Какой (четной или нечетной) является функция:

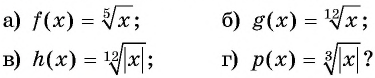
Решение:

а) Функция 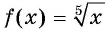 является нечетной, так как  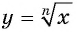при нечетном  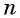есть нечетная функция.

б) Функция 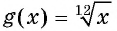 ни четная, ни нечетная, так как  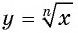при четном  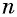не является четной и не является нечетной функцией.

в)    Так как область определения функции 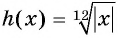 есть множество всех действительных чисел и  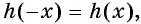то функция четная.

г)    Так как область определения функции 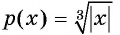 есть множество всех действительных чисел и  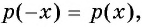то функция четная.

Пример №8

Постройте график функции:

Решение:

а) График функции 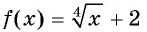 получается из графика функции  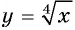сдвигом на 2 единицы вверх вдоль оси ординат (рис. 122).

б)    График функции 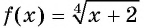 получается из графика функции 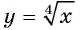сдвигом на 2 единицы влево вдоль оси абсцисс (см. рис. 122).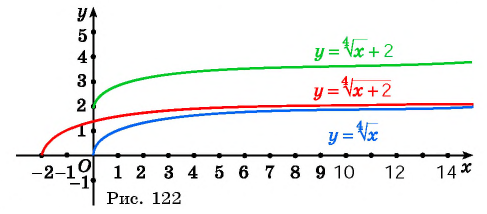  

Пример №9

Постройте график функции:

Решение:

а) График функции 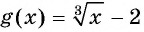 получается из графика функции  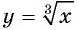сдвигом на 2 единицы вниз вдоль оси ординат ( рис. 123) 

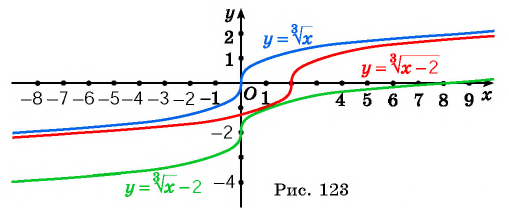
б) График функции 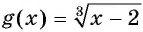 получается из графика функции  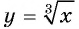сдвигом на 2 единицы вправо вдоль оси абсцисс (см. рис. 123)