Свойства функций, непрерывных в точке и на промежутке с примерами

С первыми сведениями о непрерывных и разрывных функциях вы были ознакомлены. Рассмотрим понятие непрерывности функции и свойства непрерывных функций подробнее.

Пусть функция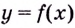 

1. в точке 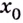 функция  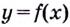определена (существует число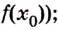 
2. в точке 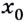 существует предел функции  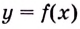(существует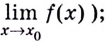 
3. в точке 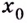 предел функции равен значению функции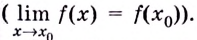 

Использование этих условий существенно упрощает вычисление пределов непрерывных функций. Для вычисления предела 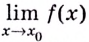 непрерывной в точке  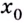функции  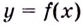достаточно вычислить значение функции в этой точке, т.е.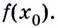 

Над непрерывными функциями можно выполнять арифметические операции.

Теорема. Пусть 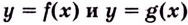 непрерывны в точке  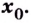Тогда их сумма, разность, произведение и частное (при условии, что знаменатель не равен нулю) тоже непрерывны в точке  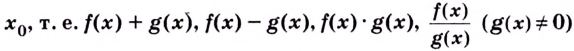- непрерывные в точке  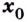функции.

Доказательство. Поскольку по определению непрерывные в точке 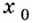 функции  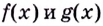имеют пределы, которые равны  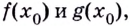то по свойству предела суммы, разности, произведения и частного пределы указанных функций существуют и соответственно равны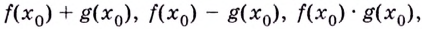 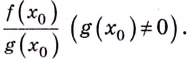 Но эти величины равны значениям соответствующих функций. Следовательно, указанные функции по определению непрерывности являются непрерывными в точке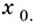 

Пример:

Для каких значений 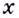 функция  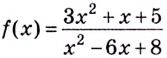будет непрерывной?

Решение:

Дробно-рациональная функция непрерывна при условии, что знаменатель не равен нулю. Уравнение 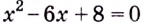 имеет корни  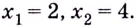Следовательно, функция непрерывна на множестве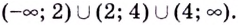 

Свойства функций, непрерывных на промежутке:

Функция называется непрерывной на промежутке, если она непрерывна в каждой его точке.

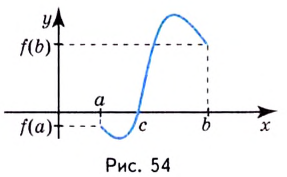
Теорема Больцано —Коши. Если функция 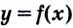 непрерывна на  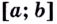и на концах этого отрезка принимает значения разных знаков, то на интервале  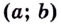обязательно существует точка  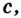такая, что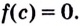 

Геометрический смысл (рис. 54) этой теоремы состоит в том, что непрерывная кривая при переходе из одной полуплоскости в другую, границей которых является ось 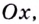 пересекает эту ось. Эта теорема применяется при решении уравнений.

Теорема Больцано—Коши (о промежуточном значении функции). Если функция 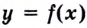 непрерывна на отрезке  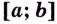и принимает на его концах разные значения, то для любого числа  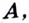находящегося между числами  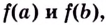на интервале  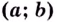обязательно существует точка  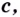такая, что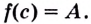 

• Заказать решение задач по высшей математике

Геометрически это означает, что прямая 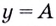 пересекает график функции  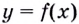по крайней мере в одной точке.

Теорема Вейерштрасса (об ограниченности непрерывной функции). Если функция 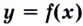 непрерывна на отрезке  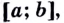то она на этом отрезке ограничена.

Теорема Вейерштрасса (о наибольшем и наименьшем значениях функции на отрезке). Если функция 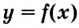 непрерывна на отрезке  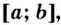то она на этом отрезке имеет наибольшее и наименьшее значения.

Замечание: Разрывные функции, вообще говоря, этих свойств не имеют.