
Свободные колебания в пассивных электрических цепях
Содержание:
Свободные колебания в пассивных электрических цепях:
Ранее уже отмечалось, что колебания в электрических цепях с реактивными элементами не могут заканчиваться сразу же после прекращения внешних воздействий на цепь, а продолжаются за счёт энергии, запасённой в реактивных элементах к моменту прекращения воздействия. Воздействие может осуществляться независимыми источниками напряжения или тока.
Определение:
Колебания в электрической цепи, происходящие после прекращения воздействия за счёт энергии, накопленной в реактивных элементах, называются свободными колебаниями, а состояние цепи при этом называется режимом свободных колебаний.
Понятно, что в пассивных электрических цепях вследствие необратимости преобразования электрической энергии в тепловую свободные колебания носят затухающий характер, поэтому режим свободных колебаний, в конечном счёте, заканчивается режимом покоя. Это означает, что пассивные электрические цепи являются устойчивыми.
Исследование процессов в электрических цепях может осуществляться как при нулевых, так и при ненулевых начальных условиях, когда значения токов в индуктивностях и напряжения на ёмкостях в момент t = 0 отличны от нуля: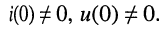
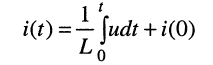
и
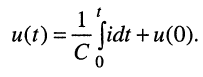 (18.2)
(18.2)
Тогда L-изображения рассматриваемых токов и напряжений (см. разд. 76.2.2), получают вид:
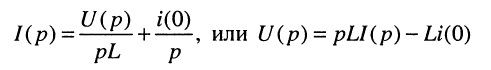 (18.3)
(18.3)
и
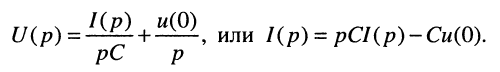 (18.4)
(18.4)
Выражения (18.3) и (18.4) показывают, что ненулевым начальным условиям цепи 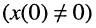 относительно некоторого процесса
относительно некоторого процесса 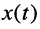 соответствует L-изображение вида:
соответствует L-изображение вида:
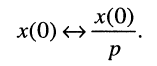 (18.5)
(18.5)
Свободные колебания в электрических цепях с одним реактивным элементом
Режим свободных колебаний в пассивной электрической цепи может рассматриваться как переходный, поскольку он завершается режимом покоя. Поэтому свободные колебания удобно изучать относительно момента 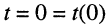 коммутации (соединения) цепи с источником; до этого момента
коммутации (соединения) цепи с источником; до этого момента 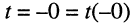 цепь отключена от источника.
цепь отключена от источника.
Свободные колебания в простейшей RC-цепи
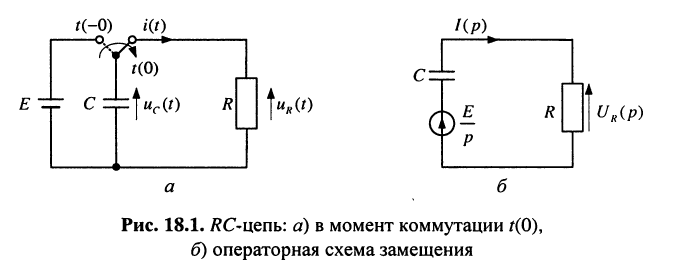
Пусть имеется цепь (рис. 18.1, а), ёмкость которой до момента коммутации была подключена параллельно источнику Е постоянного напряжения (момент 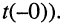 В момент
В момент 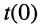 произошла коммутация и образовалась RC-цепь, напряжение на ёмкости которой равно Е.
произошла коммутация и образовалась RC-цепь, напряжение на ёмкости которой равно Е.
Задача 18.1.
Определить закон изменения тока в цепи 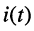 и напряжений на её элементах
и напряжений на её элементах 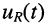 и
и 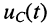 в режиме свободных колебаний.
в режиме свободных колебаний.
Решение. Поскольку напряжение на ёмкости скачком измениться не может, в цепи в момент коммутации 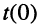 имеют место ненулевые начальные условия:
имеют место ненулевые начальные условия:
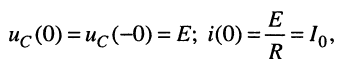
при которых напряжение на ёмкости равно напряжению источника, а ток в цепи имеет максимальное значение 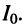
Сначала найдём закон изменения тока в цепи при разряде ёмкости от 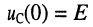 до
до 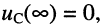 для чего воспользуемся операторным методом, предварительно составив операторную схему замещения (рис. 18.1,6) рассматриваемой цепи при ненулевых начальных условиях. В этой схеме заряженная ёмкость заменена операторной схемой замещения согласно (18.5). Теперь по закону Ома в операторной форме нетрудно найти операторный ток:
для чего воспользуемся операторным методом, предварительно составив операторную схему замещения (рис. 18.1,6) рассматриваемой цепи при ненулевых начальных условиях. В этой схеме заряженная ёмкость заменена операторной схемой замещения согласно (18.5). Теперь по закону Ома в операторной форме нетрудно найти операторный ток:
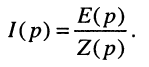 (18.6)
(18.6)
Подставляя сюда L-изображение константы
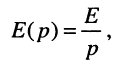
отражающей ненулевые начальные условия, и операторное сопротивление цепи
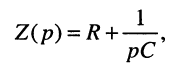 (18.7)
(18.7)
получаем выражение для операторного тока:
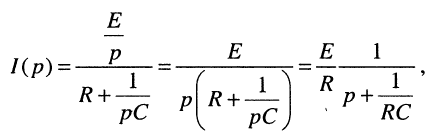 (18.8)
(18.8)
которое представляет собой L-изображение взвешенной экспоненты вида (см. табл. 16.1, строка № 7)
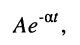
где для нашего случая:
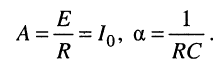
Отсюда следует закон изменения тока в цепи:
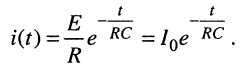 (18.9)
(18.9)
Зная ток в цепи, нетрудно вычислить напряжения на её элементах. При выбранном направлении отсчёта согласно второму закону Кирхгофа имеем:
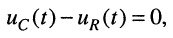
поэтому напряжения на ёмкости и резистивном элементе в любой момент одинаковы и вычисляются по формуле:
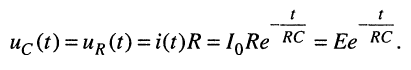 (18.10)
(18.10)
Исследуем полученные временные зависимости (18.9) и (18.10). Для удобства перейдём к нормированным величинам тока 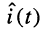 и напряжения
и напряжения 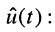
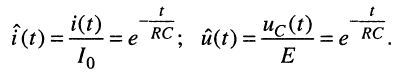
Полученные нормированные величины одинаковы, что позволяет ввести обобщённую нормированную функцию, описывающую зависимость тока и напряжения от времени:
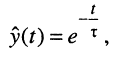 (18.11)
(18.11)
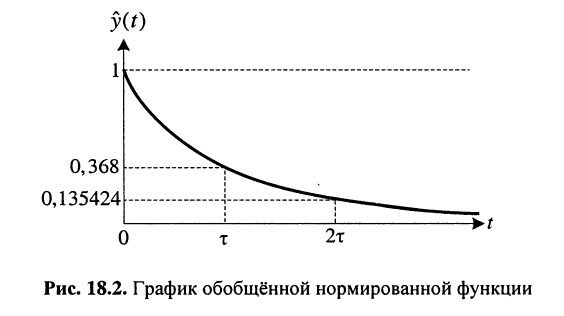
где 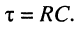 График этой функции изображён на рис. 18.2.
График этой функции изображён на рис. 18.2.
Анализ полученных результатов. Из смысла функции (18.11) и её графика видно, что ток в цепи и напряжения на ёмкостном и резистивном элементах стремятся к нулю по экспоненциальному закону, в котором существенную роль играет постоянная RC. Эта величина имеет размерность времени, она называется постоянной времени RC-цепи
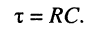 (18.12)
(18.12)
Важно:
постоянная времени (18.3) характеризует скорость изменения тока и напряжений в цепи и показывает, что на отрезке времени 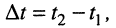 равном
равном 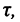 физическая величина (ток или напряжение) изменяется в
физическая величина (ток или напряжение) изменяется в
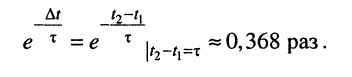
Ясно, что длительность свободных колебаний бесконечна, поскольку физические величины достигают своих предельных значений только через бесконечное время. Однако на практике принято считать свободные колебания пренебрежимо малыми, когда физическая величина 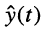 достигает уровня в диапазоне 0,05
достигает уровня в диапазоне 0,05 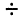 0,01 (или от 5 до 1 %).
0,01 (или от 5 до 1 %).
Определим временной диапазон процесса свободных колебаний 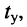 в течение которого достигаются указанные уровни тока и напряжения, для чего обратимся к неравенству
в течение которого достигаются указанные уровни тока и напряжения, для чего обратимся к неравенству
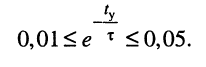
Решение этого неравенства даёт временной диапазон в пределах:
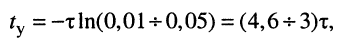
или в более привычной форме:
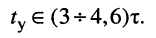 (8.13)
(8.13)
Вывод:
всё вышесказанное говорит о том, что чем больше постоянная времени, тем дольше длительность свободных колебаний в цепи, т. е. тем медленнее затухают свободные колебания.
Свободные колебания в простейшей RL-цепи
Подход к выводу закона свободных колебаний в RL-цепи подобен подходу, изложенному в предыдущем пункте.
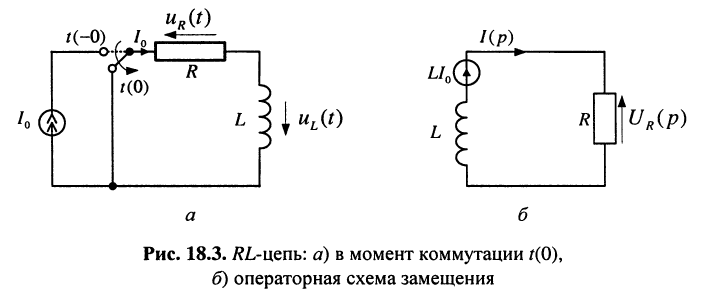
Рассмотрим цепь (рис. 18.3, а), которая до момента коммутации была подключена к источнику t(0) постоянного тока (момент t (-0)). В момент t(0) произошла коммутация и образовалась RL-цепь, в которой в момент t(0) имеют место ненулевые начальные условия:
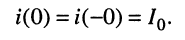
Задача 18.2.
Определить закон изменения тока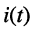 в LC-цепи и напряжений на её элементах
в LC-цепи и напряжений на её элементах 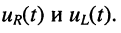
Решение. Как и в предыдущем случае, составим операторную схему замещения цепи (рис. 18.3, б), где использована схема замещения индуктивности, начальное операторное напряжение на которой
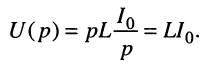
Найдём операторный ток I (р) в цепи, являющийся реакцией цепи на операторное воздействие U(p):
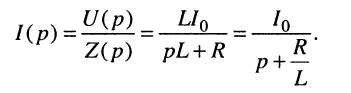
Отсюда согласно второму закону Кирхгофа в операторной форме
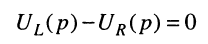
и закону Ома нетрудно получить операторные напряжения на индуктивности и резистивном элементе:
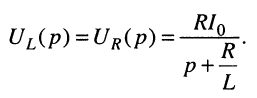
Как и в разд. 18.1.1, по таблице соответствий (см. табл. 16.1) получаем оригиналы:
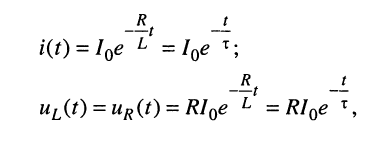
где
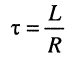
постоянная времени, имеющая тот же физический смысл, что и в случае RC-цепи.
Следовательно, в режиме свободных колебаний ток и напряжения в RL-цепи затухают также по экспоненциальному закону, и, подобно RC-цепи, это затухание происходит тем медленнее, чем больше постоянная времени.
Переходные колебания в цепях с одним реактивным элементом
В предыдущем пункте были определены законы изменения тока и напряжений в RC- и RL-цепях после отключения от цепи источника напряжения или тока. Оказалось, что токи и напряжения в этих цепях убывают до нуля по экспоненциальному закону.
Переходные колебания (переходный процесс) рассматриваются при ступенчатом воздействии (см. разд. 15.1.1) на цепь тока или напряжения и нулевых начальных условиях. Тогда, согласно определению, получаем переходную характеристику.
Поскольку в различных приложениях наиболее часто используется последовательная RС-цепь, а RL-цепь является дуальной относительно RС-цепи, будем рассматривать колебания в RС-цепи, закон изменения которых, как было показано, нетрудно распространить и на RL-цепь.
Задача 18.3.
К последовательной RС-цепи приложено ступенчатое воздействие напряжения 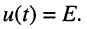 Найти законы изменения тока
Найти законы изменения тока 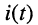 и напряжений на резистивном элементе
и напряжений на резистивном элементе 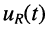 и ёмкости
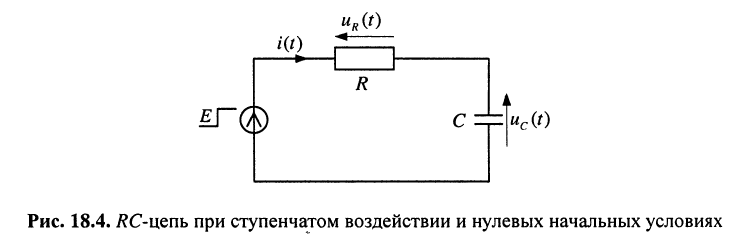
и ёмкости 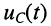 при нулевых начальных условиях (рис. 18.4).
при нулевых начальных условиях (рис. 18.4).
Важно:
формулировка задачи означает, что требуется найти переходную характеристику цепи по току и напряжениям.
Решение. В момент t = 0 включения источника напряжения в цепи согласно законам коммутации имеем:
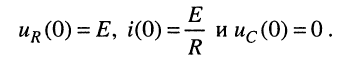
Определим операторный ток согласно закону Ома
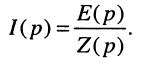 (18.14)
(18.14)
Подставим сюда операторное воздействие как L-изображение константы
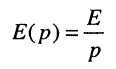
и операторное сопротивление цепи
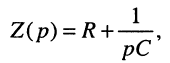
тогда получим выражение для операторного тока:
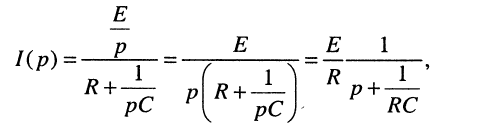 (18.15)
(18.15)
представляющее собой L-изображение взвешенной экспоненты вида 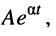 где для нашего случая
где для нашего случая
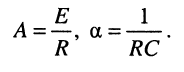
Отсюда следует закон изменения тока в цепи (рис. 18.5, а):
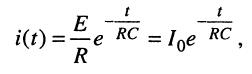 (18.16)
(18.16)
ничем не отличающийся от (18.9).
Напряжение на резистивном элементе (рис. 18.5, б) имеет вид:
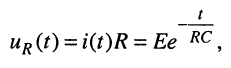 (18.17)
(18.17)
а напряжение на ёмкости (рис. 18.5,б) согласно второму закону Кирхгофа изменяется в соответствии с формулой
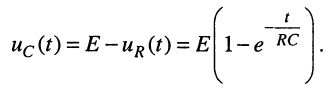 (18.18)
(18.18)
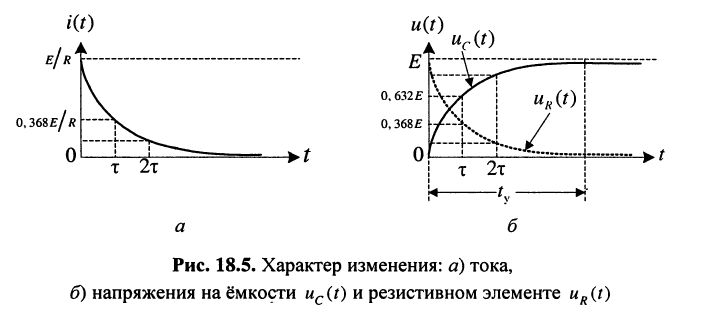
Выводы:
из полученных зависимостей и рис. 18.5 видно, что:
- ток в цепи и напряжение на резистивном элементе стремятся к нулю;
- напряжение на ёмкости возрастает, стремясь к величине приложенного напряжения Е, причём при
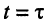 напряжение на ёмкости равно 0,632Е;
напряжение на ёмкости равно 0,632Е; - указанные изменения подчиняются экспоненциальному закону, где, как и прежде, существенную роль играет постоянная времени
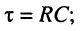
- чем больше постоянная времени, тем больше время установления состояния покоя, т. е. тем больше длительность переходного процесса;
- согласно определению (см. разд. 15.4) выражения (18.16), (18.17) и (18.18) являются переходными характеристиками
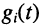 по току в цепи, по напряжению на резистивном элементе и по напряжению на ёмкости соответственно.
по току в цепи, по напряжению на резистивном элементе и по напряжению на ёмкости соответственно.
Задача 18.4.
Получить формулу (18.18) с использованием преобразования Лапласа.
Решение. Операторное напряжение на ёмкости
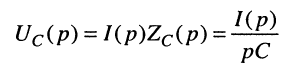
после подстановки сюда (18.14) принимает вид:
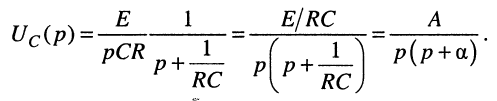
Из известного соответствия (табл. 16.1, строка № 14)
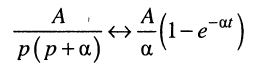
при
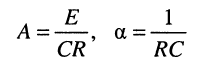
немедленно получаем оригинал
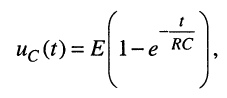
полностью совпадающий с (18.18).
Замечание
Полученные законы справедливы и для последовательной RL-цепи, имеющей постоянную времени 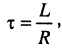 что соответствует дуальности элементов ёмкости и индуктивности.
что соответствует дуальности элементов ёмкости и индуктивности.
Задача 18.5.
Решить задачу 18.3 при ненулевых начальных условиях (рис. 18.6).
Решение. Пусть в момент t = 0 ёмкость, уже заряженная до некоторого напряжения 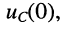 подключается к источнику ступенчатого воздействия (рис. 18.6, а). Новой схеме будет соответствовать операторная схема замещения последовательной RС-цепи (рис. 18.6, б).
подключается к источнику ступенчатого воздействия (рис. 18.6, а). Новой схеме будет соответствовать операторная схема замещения последовательной RС-цепи (рис. 18.6, б).
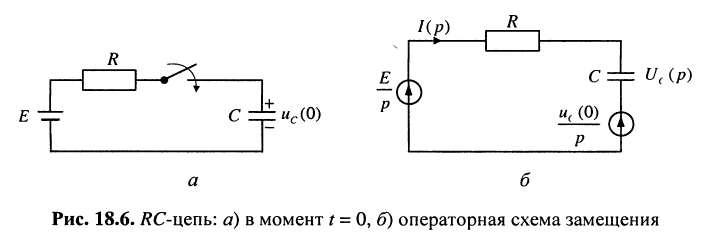
Согласно этой модели операторное напряжение на ёмкости имеет вид:
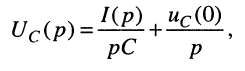 (18.19)
(18.19)
а операторный ток в цепи определяется выражением:
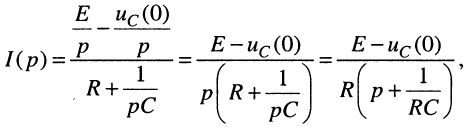 (18.20)
(18.20)
из которого, подобно (18.8), получаем оригинал:
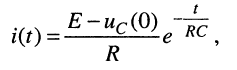 (18.21)
(18.21)
определяющий закон изменения тока в цепи.
Напряжение на резистивном элементе изменяется по экспоненциальному закону
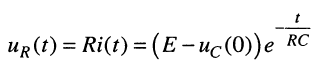 (18.22)
(18.22)
Найдём операторное напряжение на ёмкости, подставив (18.20) в (18.19):
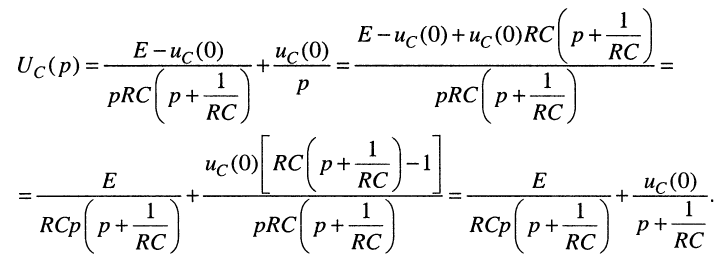
Для вычисления оригинала воспользуемся свойством линейности L-преобразования и соответствиями
(см. табл. 16.1, строки № 7 и 14):
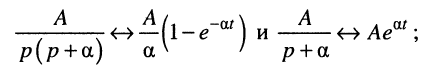
тогда получим закон изменения напряжения на емкости при ненулевых начальных условиях:
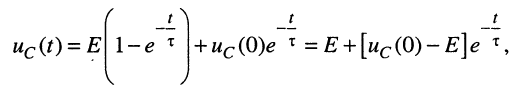 (18.23)
(18.23)
где 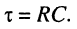
Из выражений (18.21) и (18.23) следует:
- при
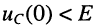 напряжение на ёмкости возрастает от
напряжение на ёмкости возрастает от 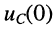 до
до 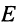 при
при 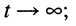
- при
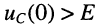 напряжение на ёмкости убывает от
напряжение на ёмкости убывает от 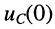 до
до 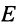 при
при 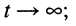
| Рекомендую подробно изучить предметы: |
| Ещё лекции с примерами решения и объяснением: |
- Цепи с распределёнными параметрами
- Волновые параметры длинной линии
- Колебания в линиях без потерь
- ЭДС и напряжение в электрической цепи
- Гармонические колебания в колебательном контуре
- Частотные характеристики линейных электрических цепей
- Частотные методы анализа и расчёта электрических цепей
- Операторные передаточные функции