
Столкновения в физике - виды, формулы и определения с примерами
Содержание:
Столкновения:
Наиболее общим явлением, наблюдаемым в природе, является взаимодействие материальных тел. Бильярдные шары, сближаясь, в момент соприкосновения взаимодействуют друг с другом. В результате этого меняются скорости шаров, их кинетические энергии. О таком взаимодействии шаров говорят как об их столкновениях.
Но понятие «столкновение» относится не только к взаимодействиям, происходящим в результате соприкосновения материальных тел. Комета, прилетевшая из отдаленных областей пространства и прошедшая в окрестности Солнца, меняет свою скорость и удаляется. Этот процесс также является столкновением. хотя непосредственного соприкосновения между кометой и Солнцем не произошло, а осуществлено оно было посредством сил тяготения.
Характерная особенность этого взаимодействия, дающая нам возможность рассматривать его как столкновение, заключается в том, что область пространства, в котором оно произошло, относительно мала. Заметное изменение скорости кометы происходит вблизи Солнца (рис. 129).
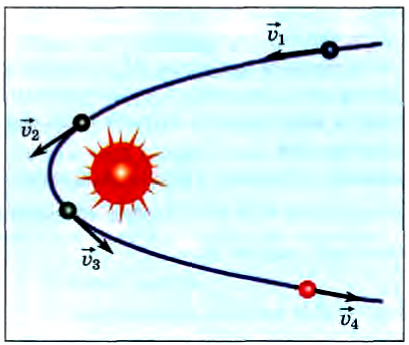
Приведенные примеры позволяют нам дать следующее определение столкновения.
Что такое столкновение
Столкновением называется взаимодействие двух и большего числа тел, которое происходит в относительно малой области пространства в течение относительно малого промежутка времени. Вне этого промежутка времени можно говорить о начальных и конечных импульсах тел, когда тела можно считать невзаимодействующими.
Столкновение материальных тел часто называется ударом. Удар определяется как процесс, при котором изменяются импульсы соударяющихся тел без существенного изменения их положений. Это частный случай столкновения, например столкновение шаров, шайб, автомобилей и т. п.
Процессы столкновения являются чрезвычайно сложными. Например, при столкновении двух шаров в момент их соприкосновения начинается деформация шаров. В результате часть кинетической энергии переходит в потенциальную энергию деформации. Затем энергия деформации снова превращается в кинетическую, однако не полностью — часть энергии превращается во внутреннюю. Кроме того, после столкновения шары будут вращаться по иному, чем до столкновения.
Главный интерес при рассмотрении столкновений заключается в знании не самого процесса, а результата. Ситуация до столкновения называется начальным состоянием, а после — конечным. Между величинами, характеризующими начальное и конечное состояния, соблюдаются определенные соотношения. независящие от детального характера взаимодействия. Такими величинами. в частности, являются импульс и энергия системы тел.
В зависимости от характера изменения кинетической энергии тел все столкновения делятся на упругие и неупругие.
Если при столкновении кинетическая энергия тел сохраняется, то столкновение называется упругим, если же не сохраняется — неупругим.
Рассмотрим вначале абсолютно неупругое столкновение (абсолютно неупругий удар). Это частный случай неупругого столкновения, при котором после столкновения тела «слипаются» и движутся вместе.
Пусть в некоторой инерциальной системе отсчета первое тело массой m1 движется до столкновения со скоростью υ1, а второе тело массой m2 — со скоростью υ2. Следовательно, импульсы тел до столкновения равны соответственно: 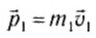
Процесс столкновения обычно наглядно представляют с помощью векторной диаграммы импульсов (рис. 130). Нетрудно убедиться, что кинетическая энергия системы не сохраняется. До столкновения она составляет:
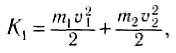
после столкновения —
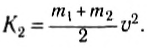
Изменение кинетической энергии:
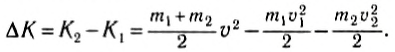 (2)
(2)
Для расчета выберем оси координат так, как показано на рисунке 130, и спроектируем на них равенство (1). B результате получим:
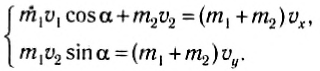
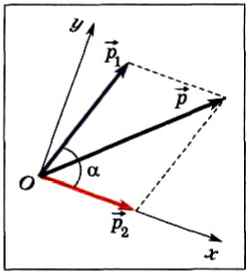
Рис. 130
Отсюда легко находится квадрат скорости тел после столкновения:
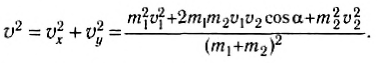
Подставив полученное выражение в (2), получим после несложных преобразований:
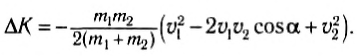
Как видно, кинетическая энергия системы уменьшилась. Часть кинетической энергии превратилась в теплоту.
Если тела при столкновении не «слипаются», то скорости тел после столкновения можно найти из закона сохранения импульса:
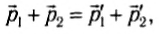
где штрихом отмечены импульсы тел после столкновения.
При этом кинетическая энергия может как уменьшаться, так и увеличиваться. Последнее происходит, например, при различных взрывах. В этом случае часть внутренней энергии превращается в кинетическую энергию осколков.
Как уже отмечалось, при упругом столкновении выполняется закон сохранения импульса и механической энергии.
Рассмотрим вначале лобовое столкновение, т. е. такое столкновение, при котором импульсы тел до и после столкновения параллельны некоторой прямой. Эту прямую мы примем за ось Ox (рис. 131). Закон сохранения импульса в этом случае примет вид:
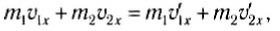
а закон сохранения кинетической энергии -
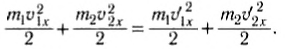
Из этих уравнений найдем скорости тел после удара. Для этого перепишем (3) и (4) следующим образом:
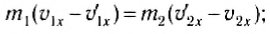
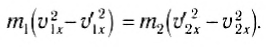
Воспользовавшись тем, что a2 - b2 = (a-b)(a + b), из выражений (5) и (6) легко получить:
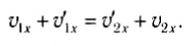
Выразив отсюда, например, 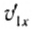 и подставив его в (5), после несложных преобразований находим:
и подставив его в (5), после несложных преобразований находим:
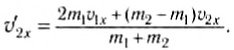
Аналогично:
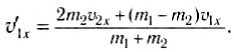
Проекции импульсов тел после столкновения равны соответственно:
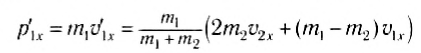
и
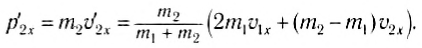
Проанализируем полученные выражения для некоторых частных случаев.
Предположим, что тело 2 до столкновения покоилось, т. е. 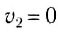 .
.
Тогда
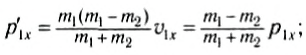
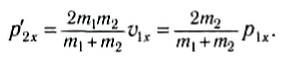
При равных массах тел m1 = m2 получим:
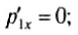
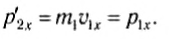
Значит, первое тело остановится, а второе придет в движение с таким же импульсом.
Теперь предположим, что масса второго тела намного больше массы первого. Тогда, пренебрегая m1 по сравнению с m2 , получим:
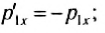
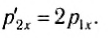
Значит, первое тело отскочит назад с таким же по модулю импульсом, а тело 2 получит импульс, равный удвоенному значению импульса первого тела.
Найдем кинетическую энергию тел после столкновения для случая, когда 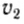 = 0:
= 0:
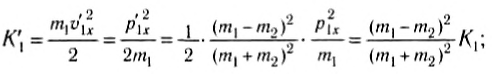 (10)
(10)
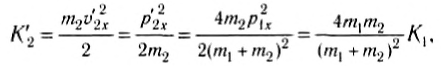 (10)
(10)
где K1 — кинетическая энергия первого тела до столкновения.
Из полученных выражений следует, что при m1 = m2 первое тело останавливается, а второе приобретает ту же энергию. Если масса второго тела m2 намного больше массы первого m1 то из (10) и (11) следует, что 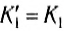 ,
, 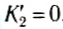 . Значит, кинетическая энергия первого тела не изменяется, а второе тело получает импульс, но его энергия не изменяется.
. Значит, кинетическая энергия первого тела не изменяется, а второе тело получает импульс, но его энергия не изменяется.
Главные выводы:
- Столкновением называется взаимодействие двух и большего числа тел, которое происходит в относительно малой области пространства в течение относительно малого промежутка времени.
- Удар определяется как процесс, при котором изменяются импульсы соударяющихся тел без существенного изменения их положений.
- Столкновение тел называется упругим, если кинетическая энергия тел сохраняется. При неупругом столкновении кинетическая энергия тел не сохраняется.
- При столкновениях тел выполняется закон сохранения импульса.
Определение столкновения
Законы сохранения энергии и импульса позволяют провести теоретическое исследование процессов столкновения тел без описания сил, действующих между ними.
Под столкновениями понимают механические процессы взаимодействия между телами, происходящие за очень короткий промежуток времени. При этом силы взаимодействия между сталкивающимися телами настолько велики, что внешними силами, действующими на систему, можно пренебречь.
Вследствие того, что длительность столкновения мала по сравнению со временем наблюдения, различают механические состояния до и после столкновения, причем тела, находящиеся на большом расстоянии друг от друга, считают свободными.
Длительность столкновения бильярдных шаров 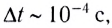 что намного меньше характерного времени движения шаров по столу
что намного меньше характерного времени движения шаров по столу 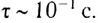
Различают упругие (абсолютно упругие) и неупругие столкновения. В первом случае не происходит выделения теплоты, и механическая энергия сохраняется. Во втором случае выделяется некоторое количество теплоты, поэтому механическая энергия после столкновения уменьшается.
Примером упругих столкновений служат столкновения металлических шаров, а примером неупругих — столкновения пластилиновых шаров, которые при этом слипаются и продолжают движение как одно целое.
Для макроскопических тел в большей степени характерными являются неупругие столкновения, в то время как для физики элементарных частиц, ядер атомов, молекул определяющую роль играет упругое взаимодействие.
Если в процессе столкновения тел на них не действуют внешние силы, то к телам применим закон сохранения импульса, а во многих случаях — и закон сохранения механической энергии. Именно эти законы позволяют, зная скорости тел до столкновения, определить их скорости после столкновения, совершенно не интересуясь тем, что происходило во время него.
При абсолютно неупругом столкновении скорости обоих взаимодействующих тел оказываются одинаковыми. Примером таких тел являются тела из различных пластичных веществ. Такое столкновение можно наблюдать, если подвесить тары из пластилина, развести их в разные стороны и отпустить. После столкновения они оба будут двигаться вместе с одинаковой скоростью.
При абсолютно упругом столкновении в обоих телах не остается никаких деформаций. Кроме того, вся кинетическая энергия, которой тела обладали до столкновения, снова превращается в кинетическую энергию. Примерами таких тел являются шары из стали или слоновой кости.
Рассмотрим простейшее столкновение — центральное, когда скорости тел находятся на линии, соединяющей их центры. Очень часто такое столкновение называют лобовым.
Скорость движения 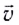 после абсолютно неупругого столкновения тел массами
после абсолютно неупругого столкновения тел массами 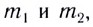 движущихся до столкновения со скоростями
движущихся до столкновения со скоростями 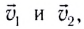 можно определить из закона сохранения импульса:
можно определить из закона сохранения импульса:
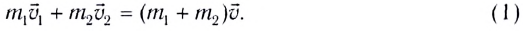
Откуда находим
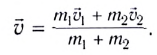
Определим «потери» механической энергии, найдя кинетическую энергию
тел до столкновения:
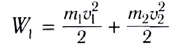
и после столкновения:
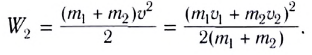
Тогда часть механической энергии, перешедшая во внутреннюю, определяется выражением:
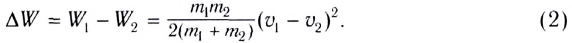
Следовательно, она зависит от масс сталкивающихся тел и относительной скорости 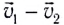 их движения до столкновения.
их движения до столкновения.
Задача о центральном абсолютно неупругом столкновении впервые была решена Дж. Валлисом в 1669 г.
При абсолютно упругом столкновении двух тел массами 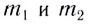 на основании закона сохранения импульса и закона сохранения энергии можно записать
на основании закона сохранения импульса и закона сохранения энергии можно записать
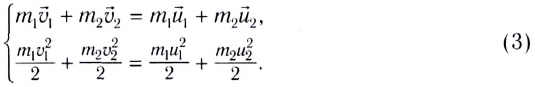
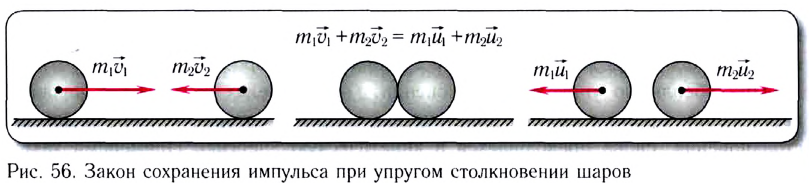
Здесь 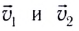 — скорости тел до столкновения,
— скорости тел до столкновения, 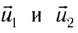 — после столкновения.
— после столкновения.
Преобразуем систему уравнений (3), перенеся в правую часть все величины, относящиеся к первому телу, а в левую — ко второму:
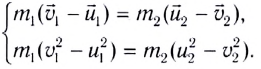
Разделив второе уравнение на первое, получим

Перепишем это уравнение в виде 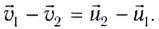 .
.
Из него следует, что при центральном абсолютно упругом столкновении тел любой массы их относительная скорость до и после столкновения не изменяется.
Теперь можно дать еще одно определение неупругого столкновения: если относительная скорость тел при центральном столкновении изменяется, то такое столкновение называется неупругим.
Меру неупругости k можно определить как отношение относительных скоростей сталкивающихся тел после и до столкновения: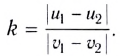
Она называется коэффициентом восстановления и впервые была измерена Ньютоном в 1687 г. В частности, Ньютон получил значения коэффициента для стали k = 0,55 и стекла k = 0,94, которые приводят и современные справочники.
Абсолютно неупругим является столкновение, при котором скорости тел после столкновения равны 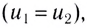 т. е. k = 0.
т. е. k = 0.
Решая уравнение (4) совместно с первым уравнением системы (3), находим скорости тел после столкновения:
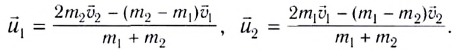
На самом деле при столкновении всегда происходят «потери» механической энергии, т. е. переход части ее в теплоту. Но при малых «потерях» действительный процесс достаточно хорошо описывается абсолютно упругим столкновением.
Задача о центральном абсолютно упругом столкновении впервые была решена X. Гюйгенсом и К. Реном в 1669 г.
Отметим, что осуществить центральное, или лобовое, столкновение на практике очень трудно. Подавляющее число столкновений являются нецентральными.
Основные формулы
Импульс тела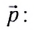
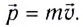
Закон изменения импульса системы тел:
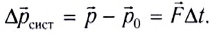
Закон сохранения импульса системы тел:
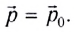
Работа: 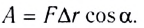
Средняя мощность: 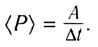
Мгновенная мощность: 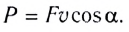
Кинетическая энергия: 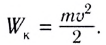
Теорема о кинетической энергии:
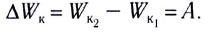
Потенциальная энергия: 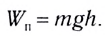
Потенциальная энергия упруго деформированного тела:
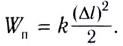
Закон сохранения механической энергии:
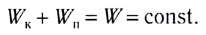
| Рекомендую подробно изучить предметы: |
| Ещё лекции с примерами решения и объяснением: |