
Степень с целым показателем с примерами решения
Содержание:
Степень с целым показателем — это степень, показателем которой является любое целое число и эти целые числа могут быть, положительными и отрицательными.
Определение и основные свойства степени с целым показателем
Для любого действительного числа 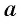
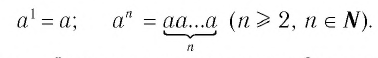
Для любого действительного числа 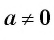 полагаем
полагаем
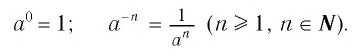
Свойства действий над степенями с целыми показателями
Свойства действий над степенями с целыми показателями сформулированы в следующей теореме.
Теорема 1.
Для любых значений 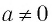 и
и 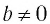 при любых целых
при любых целых 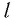 и
и 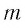 верны равенства:
верны равенства:
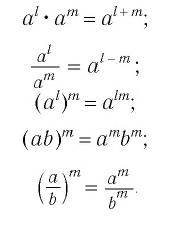
Сформулируем также теорему о возведении в степень обеих частей неравенства.
Теорема 2.
Пусть 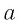 и
и 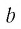 — неотрицательные числа,
— неотрицательные числа, 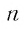 — натуральное число. Тогда:
— натуральное число. Тогда:
- если
 то
то 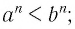
- если
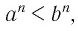 то
то 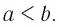
Доказательство:
Проведем доказательство методом от противного.
Допустим, что неравенство 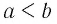 неверное. Тогда верно одно из двух соотношений:
неверное. Тогда верно одно из двух соотношений: 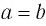 или
или 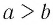 .
.
Если 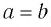 , то
, то 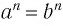 . Это противоречит условию.
. Это противоречит условию.
Если 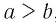 , то согласно первой части этой теоремы
, то согласно первой части этой теоремы 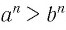 . Опять получили противоречие с условием.
. Опять получили противоречие с условием.
Значит, 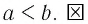
Пример №1
Сравнить числа 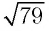 и 9.
и 9.
Решение:
Поскольку 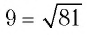 и верно неравенство
и верно неравенство 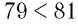 , т. е.
, т. е. 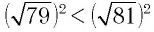 , то по теореме 2 будет верным и неравенство
, то по теореме 2 будет верным и неравенство 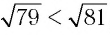 , т. е.
, т. е. 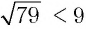 .
.
Ответ: 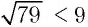 .
.
Пример №2
Известно, что 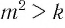 . Верно ли неравенство
. Верно ли неравенство 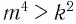 ?
?
Решение:
Если 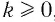 , то из верного неравенства
, то из верного неравенства 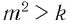 следует, что верно и неравенство
следует, что верно и неравенство 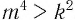 .
.
Если 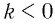 , то гарантировать, что, когда верно неравенство
, то гарантировать, что, когда верно неравенство 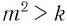 , будет верным и неравенство
, будет верным и неравенство 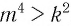 , нельзя. Например, неравенство
, нельзя. Например, неравенство 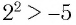 верное, а неравенство
верное, а неравенство 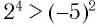 неверное.
неверное.
Следствие:
Пусть 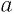 и
и 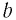 — числа одного знака,
— числа одного знака, 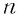 — натуральное число. Тогда, если
— натуральное число. Тогда, если 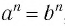 , то
, то 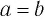 .
.
Доказательство:
Проведем его методом от противного. Допустим, что 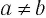 , например
, например 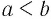 .
.
Если 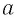 и
и 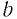 — положительные числа, то согласно теореме 2 верно неравенство
— положительные числа, то согласно теореме 2 верно неравенство 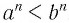 . Получили противоречие с условием. Значит,
. Получили противоречие с условием. Значит, 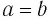 . Если
. Если 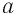 и
и 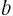 — отрицательные числа, то
— отрицательные числа, то 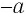 и
и 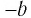 — положительные числа, и если
— положительные числа, и если 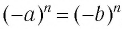 , то, как только что было доказано,
, то, как только что было доказано, 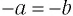 , а значит,
, а значит, 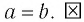
И Заметим, что при использовании этого следствия необходимо проверять совпадение знаков 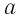 и
и 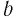 при четном
при четном 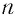 , а при нечетном
, а при нечетном 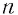 такой необходимости нет.
такой необходимости нет.
Пример №3
Верно ли, что 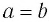 , если:
, если:
а) 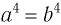 ; б)
; б)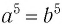 ?
?
Решение:
а) Верно, если 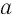 и
и 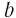 — числа одного знака, и неверно, если они разных знаков. Например,
— числа одного знака, и неверно, если они разных знаков. Например, 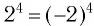 — верное числовое равенство, но равенство
— верное числовое равенство, но равенство 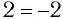 — неверное.
— неверное.
б) Поскольку число и его нечетная степень всегда имеют один и тот же знак, то из того, что 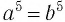 — верное числовое равенство, следует равенство чисел
— верное числовое равенство, следует равенство чисел 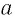 и
и 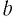 .
.
Пример №4
Выполнить действия:
а) 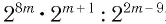 ; б)
; б) 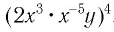 .
.
Решение:
а )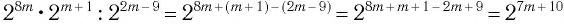 .
.
б) 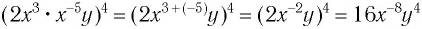 .
.
| Рекомендую подробно изучить предметы: |
| Ещё лекции с примерами решения и объяснением: |
- Корень n-й степени
- Тождества с корнями, содержащие одну переменную
- Действия с корнями нечетной степени
- Действия с корнями четной степени
- Показательно-степенные уравнения и неравенства
- Показательные уравнения и неравенства
- Логарифмические уравнения и неравенства
- Степенная функция - определение и вычисление