Степень с рациональным показателем с примерами решения
Содержание:
Напомним, что каждое рациональное число можно записать в виде дроби 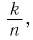
Определение. Пусть 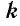 — целое число,
— целое число, 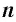 — натуральное число, не равное 1. Степенью положительного числа а с рациональным показателем
— натуральное число, не равное 1. Степенью положительного числа а с рациональным показателем 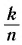 (обозначается
(обозначается 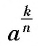 ) называется положительный корень и-й степени из числа
) называется положительный корень и-й степени из числа 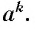
Таким образом, 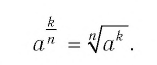
Степень с рациональным показателем определяется и для основания, равного нулю (а = 0), но только тогда, когда показатель положительный.

Примеры преобразования степеней с рациональными показателями
Приведем несколько примеров преобразования степеней с рациональными показателями:
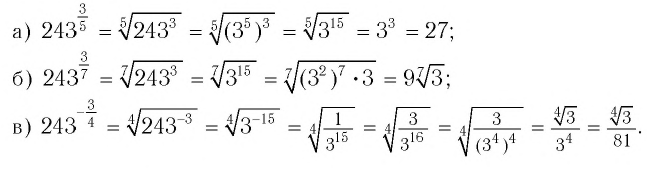
Выражения 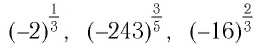 не имеют смысла, так как по определению основание степени с рациональным показателем может быть только неотрицательным.
не имеют смысла, так как по определению основание степени с рациональным показателем может быть только неотрицательным.
Поскольку рациональное число представимо в виде дроби неоднозначно, то возникает вопрос: не зависит ли определение степени с рациональным показателем от вида этой дроби? Например, верно ли равенство
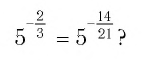
На этот вопрос отвечает следующая теорема.
Теорема:
Для любого положительного значения 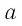 при любом натуральном
при любом натуральном 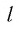 верно равенство
верно равенство
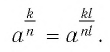
Доказательство:
Преобразуем правую часть этого равенства, используя определение степени c. рациональным показателем, а также свойства степеней и корней:
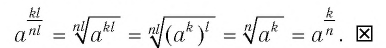
Возникает вопрос: если, например, вычислить 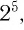 пользуясь определением степени с целым показателем, и вычислить
пользуясь определением степени с целым показателем, и вычислить 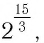 пользуясь определением степени с рациональным показателем, то получим ли мы одно и то же число?
пользуясь определением степени с рациональным показателем, то получим ли мы одно и то же число?
На этот вопрос отвечает следующая теорема.
Теорема:
Для любого положительного значения а при любом натуральном 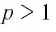 и целом
и целом 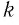 верно равенство
верно равенство
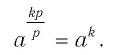
Доказательство:
Преобразуем левую часть этого равенства, пользуясь определением степени с рациональным показателем, а также свойствами степеней и корней:
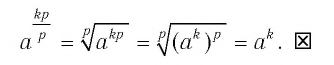
Действия со степенями с рациональными показателями
Для положительных оснований все действия со степенями с рациональными показателями обладают теми же свойствами, что и действия со степенями с целыми показателями.
Теорема:
Для любых положительных значений 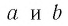 при любых рациональных
при любых рациональных 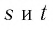 верны равенства:
верны равенства:
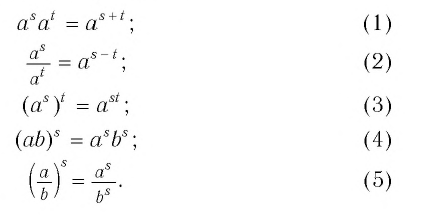
Доказательство:
Пусть 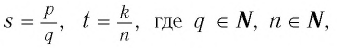
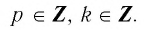
Докажем равенство (1). Преобразуем его левую часть:
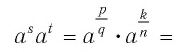
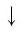 по теореме 1 из п. 1.8 получим
по теореме 1 из п. 1.8 получим 
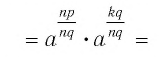
 по определению степени с рациональным показателем имеем
по определению степени с рациональным показателем имеем 
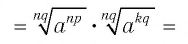
 по теоремам из п. 1.4, 1.5 имеем
по теоремам из п. 1.4, 1.5 имеем
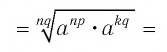
 по свойству степеней с целыми показателями получим
по свойству степеней с целыми показателями получим 
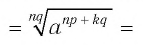
 по определению степени с рациональным показателем имеем
по определению степени с рациональным показателем имеем
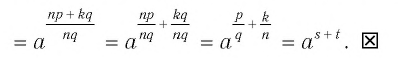
Доказательство остальных равенств аналогично доказательству равенства (1). ▲
Замечание 1. Согласно теореме 2 из п. 1.8 доказанные в этом пункте утверждения верны и в случае, когда одно из чисел 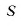 или
или 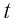 целое.
целое.
Замечание 2. Равенства (1)—(5) являются тождествами, поскольку каждое из них превращается в верное числовое равенство при любых значениях переменных, при которых входящие в это равенство выражения имеют смысл.
Следствие:
Для любых положительных значений 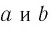 при любом рациональном
при любом рациональном 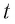 верны равенства:
верны равенства:
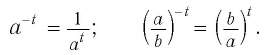
▲ Докажите эти равенства самостоятельно, используя равенства (2) и (5). ▲
Пример №1
Найти значение выражения 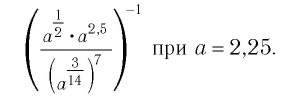
Решение:
Выполним преобразования:
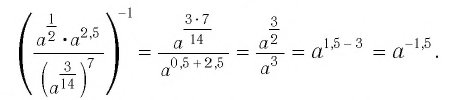
При 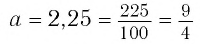 получим
получим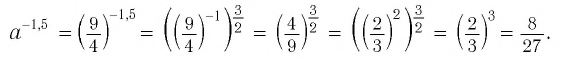
Ответ: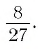
Пример №2
Пусть 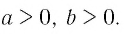 Разложить выражение
Разложить выражение 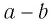 на множители как разность:
на множители как разность:
а) квадратов; б)* кубов; в) четвертых степеней.
Решение:
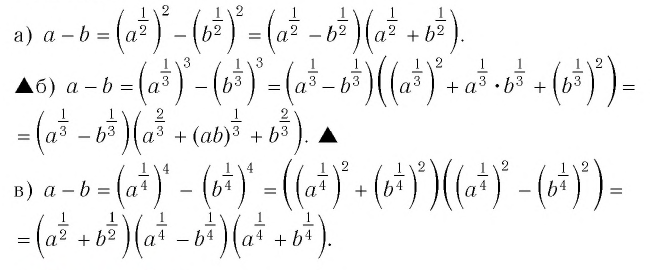
Пример №3
Сократить дробь
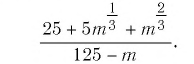
Решение:
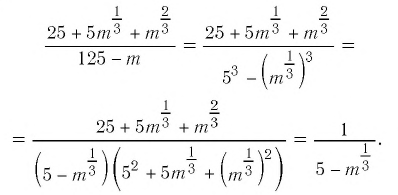
Ответ: 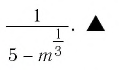
Пример №4
Найти значение выражения
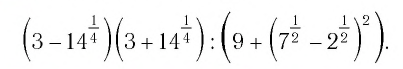
Решение:
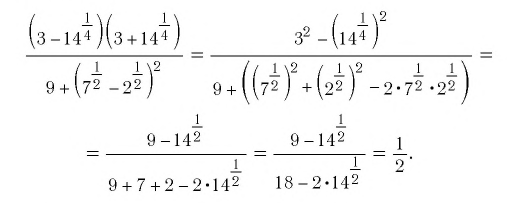
Ответ: 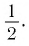
Сравнение степеней с рациональными показателями
Теорема:
Пусть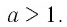 Тогда:
Тогда:
- если
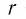 — положительное рациональное число, то
— положительное рациональное число, то 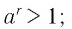
- если
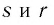 — рациональные числа и
— рациональные числа и 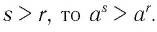
Доказательство:
Докажем утверждение 1). Положительное рациональное число 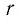 можно представить в виде
можно представить в виде 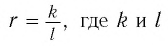 — натуральные числа.
— натуральные числа.
По условию 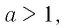 значит, согласно свойству степеней с натуральными показателями получим
значит, согласно свойству степеней с натуральными показателями получим 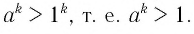 Последнее неравенство можно переписать так:
Последнее неравенство можно переписать так:
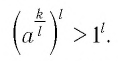
Еще раз воспользовавшись свойством степеней с натуральными показателями, получим
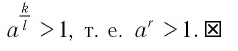
Утверждение 2) доказывается аналогично.
Теорема:
Пусть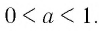 Тогда:
Тогда:
- если
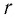 — положительное рациональное число, то
— положительное рациональное число, то 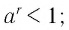
- если
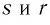 — рациональные числа и
— рациональные числа и 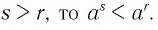
Доказательство этой теоремы аналогично доказательству теоремы 1.
Пример №5
Сравнить значения выражений:
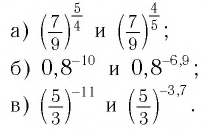
Решение:
а) Основание степеней 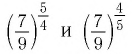 — число —
— число — 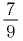
положительно и меньше 1, при этом показатель — больше показателя 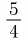 В этом случае большему значению показателя соответствует меньшее значение степени. Поэтому имеем
В этом случае большему значению показателя соответствует меньшее значение степени. Поэтому имеем
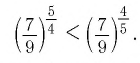
б)Для основания степеней и их показателей соответственно верны неравенства
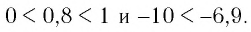
В этом случае большему значению показателя соответствует меньшее значение степени. Поэтому имеем
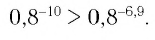
в) Для основания степеней и их показателей соответственно верны неравенства
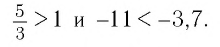
В этом случае большему значению показателя соответствует большее значение степени. Поэтому имеем
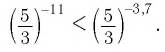
Пример №6
Сравнить 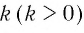 с единицей, если известно, что верно неравенство:
с единицей, если известно, что верно неравенство:
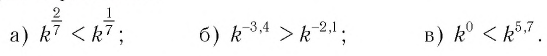
Решение:
а) Поскольку для показателей степеней верно неравенство 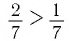 и по условию большему значению показателя степени соответствует меньшее значение степени, то основание степени
и по условию большему значению показателя степени соответствует меньшее значение степени, то основание степени 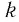 удовлетворяет неравенству
удовлетворяет неравенству 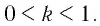
б) Поскольку для показателей степени верно неравенство 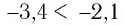 и по условию большему значению показателя соответствует меньшее значение степени, то основание степени
и по условию большему значению показателя соответствует меньшее значение степени, то основание степени 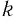 удовлетворяет неравенству
удовлетворяет неравенству 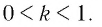
в) Поскольку для показателей степеней верно неравенство 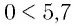 и по условию большему значению показателя соответствует большее значение степени, то основание степени
и по условию большему значению показателя соответствует большее значение степени, то основание степени 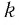 удовлетворяет неравенству
удовлетворяет неравенству 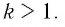
Ответ: 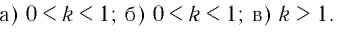
Степенная функция (показатель положительный)
В предыдущих классах мы изучали функции 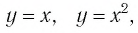
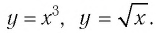 Каждая из них является частным случаем функции
Каждая из них является частным случаем функции 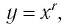
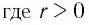 — постоянная.
— постоянная.
Такая функция называется степенной.
Рассмотрим степенные функции с различными положительными показателями.
Функция y=xr где r=2k, k∈N
1. Функция 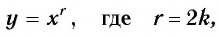
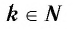
Естественная область определения выражения 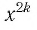 — множество R всех действительных чисел. Оно и является областью определения функции
— множество R всех действительных чисел. Оно и является областью определения функции 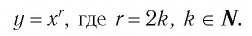
Назовем свойства функции 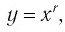 где
где 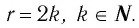 . Они те же, что и у функции
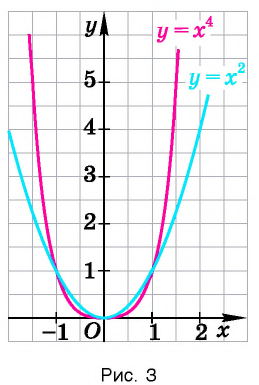
. Они те же, что и у функции 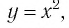 и устанавливаются так же, как свойства этой функции. Для сравнения графики функций
и устанавливаются так же, как свойства этой функции. Для сравнения графики функций 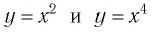 изображены на рисунке 3.
изображены на рисунке 3.
Теорема (о свойствах функции 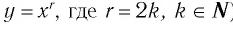 )
)
- Областью определения функции является множество R всех действительных чисел.
- Множеством (областью) значений функции является промежуток
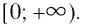
- Значение функции, равное нулю (у = 0), является наименьшим, а наибольшего значения функция не имеет.
- График функции имеет с осями координат единственную точку пересечения (0; 0) — начало координат.
- Значение аргумента, равное нулю (х = 0), является нулем функции.
- Функция принимает положительные значения (у > 0) на множестве
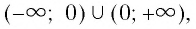 т. е. все точки графика, кроме начала координат, лежат выше оси Ох, в I и II координатных углах.
т. е. все точки графика, кроме начала координат, лежат выше оси Ох, в I и II координатных углах. - Функция четная; график функции симметричен относительно оси ординат.
- Функция убывающая на промежутке
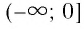 и возрастающая на промежутке
и возрастающая на промежутке 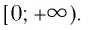
- Функция не является периодической.
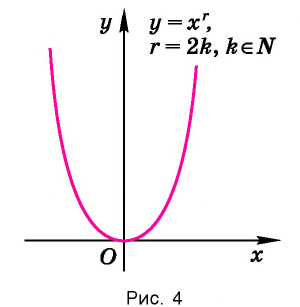
Убедитесь в справедливости этих свойств, используя схематичное изображение графика функции 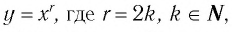 на рисунке 4.
на рисунке 4.
Замечание. Если 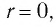 то функция
то функция 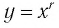 имеет вид
имеет вид 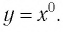
Естественная область определения выражения 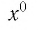 — множество
— множество 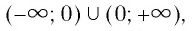 т. е. все значения переменной
т. е. все значения переменной 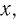 кроме нуля
кроме нуля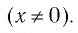 На этой области определения функция
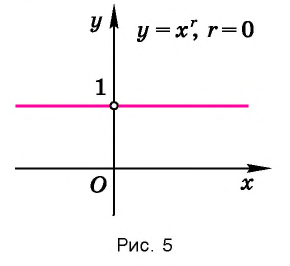
На этой области определения функция 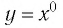 имеет постоянное значение, равное 1. Изображение графика этой функции дано на рисунке 5.
имеет постоянное значение, равное 1. Изображение графика этой функции дано на рисунке 5.
Функция y=xr где r=2k+1, k∈N
2. Функция 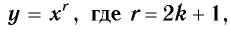
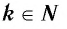
Естественная область определения выражения 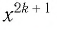 множество R
множество R
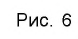
Всех действительных чисел. Оно и является областью определения функции
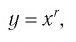
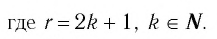
Назовем свойства функции 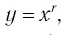 где
где 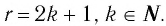 Они те же, что и у функции
Они те же, что и у функции 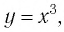 и устанавливаются так же, как свойства этой функции. Для сравнения графики функций
и устанавливаются так же, как свойства этой функции. Для сравнения графики функций 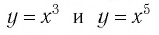 ъ изображены на рисунке 6.
ъ изображены на рисунке 6.
Теорема (о свойствах функции 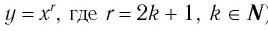 )
)
- Областью определения функции является множество R всех действительных чисел.
- Множеством (областью) значений функции является множество R всех действительных чисел.
- Функция наименьшего и наибольшего значений не имеет.
- График функции пересекает оси координат в единственной точке (0; 0) — начале координат.
- Значение аргумента, равное нулю (х = 0), является нулем функции.
- Функция принимает отрицательные значения (у < 0) на промежутке
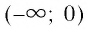 и положительные значения (у > 0) на промежутке
и положительные значения (у > 0) на промежутке 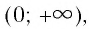 т. е. график функции расположен в I и III координатных углах.
т. е. график функции расположен в I и III координатных углах. - Функция нечетная; график функции симметричен относительно начала координат.
- Функция возрастающая на области определения.
- Функция не является периодической.
Убедитесь в справедливости этих свойств, используя схематичное изображение графика функции 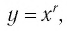 где
где 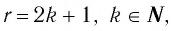 на рисунке 7.
на рисунке 7.
Пример №7
Сравнив схематичные изображения графиков функций 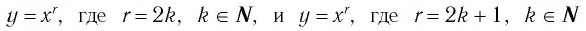 (см. рис. 4, 7), указать, на каком из множеств обе функции:
(см. рис. 4, 7), указать, на каком из множеств обе функции:
а) возрастают;
б) имеют значения разных знаков;
в) убывают;
г) принимают неотрицательные значения;
д) принимают положительные значения;
е) принимают равные значения.
Ответ:
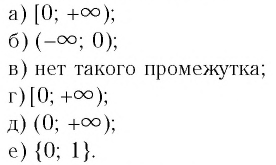
Замечание. Если 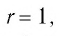 то функция
то функция 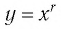 совпадает с функцией
совпадает с функцией 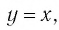 график которой изображен на рисунке 8.
график которой изображен на рисунке 8. 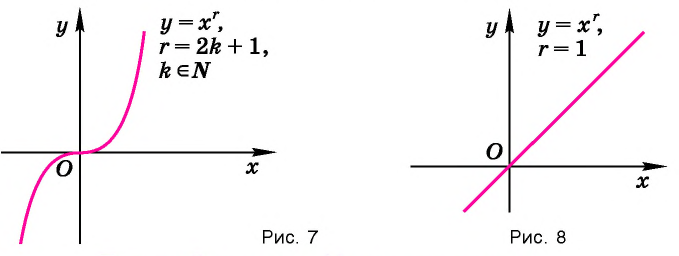
Функция y=xr, где r- рациональное нецелое число больше 1, r ∈ Q, r ∉ Z, r > 1
3. Функция 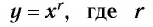 — рациональное нецелое число больше
— рациональное нецелое число больше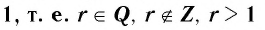
Область определения этой функции — промежуток 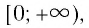 т. е. эта функция рассматривается только на множестве всех неотрицательных действительных чисел.
т. е. эта функция рассматривается только на множестве всех неотрицательных действительных чисел.
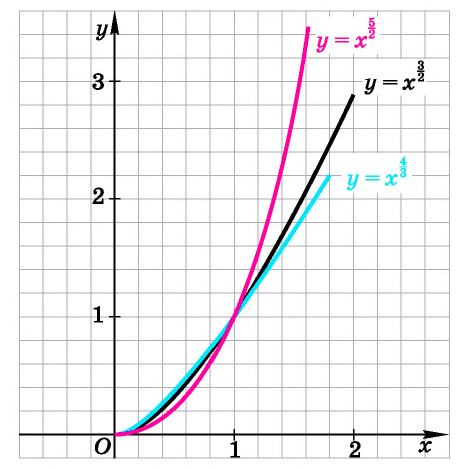
Назовем свойства этой функции. Для сравнения графики функций 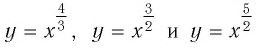 изображены на рисунке 9.
изображены на рисунке 9.
Теорема (о свойствах функции 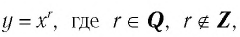
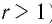 )
)
- Областью определения функции является множество
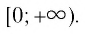
- Множеством (областью) значений функции является множество
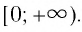
- Значение функции, равное нулю
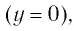 является наименьшим, а наибольшего значения функция не имеет.
является наименьшим, а наибольшего значения функция не имеет. - График функции имеет с осями координат единственную общую точку (0; 0) — начало координат.
- Значение аргумента, равное нулю (х = 0), является нулем функции.
- Функция принимает положительные значения (у > 0) на промежутке
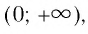 т. е. график функции расположен в I координатном угле.
т. е. график функции расположен в I координатном угле. - Функция не является ни четной, ни нечетной.
- Функция возрастающая на области определения.
- Функция не является периодической.
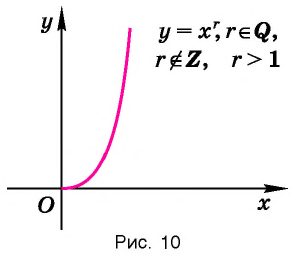
Убедитесь в справедливости этих свойств, используя схематичное изображение графика функции 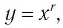 где
где 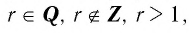 на рисунке 10.
на рисунке 10.
Функция y=xr, где r- рациональное положительное число меньше 1
4. Функция 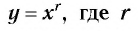 — рациональное положительное число меньше 1, т. е.
— рациональное положительное число меньше 1, т. е. 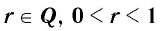
Область определения этой функции — промежуток 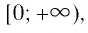 т.е. эта функция рассматривается только на множестве всех неотрицательных действительных чисел.
т.е. эта функция рассматривается только на множестве всех неотрицательных действительных чисел.
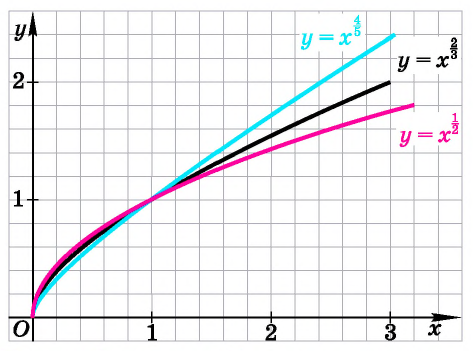
Для сравнения графики функций 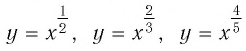 изображены на рисунке (рис. 11).
изображены на рисунке (рис. 11).
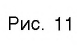
Свойства функции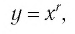
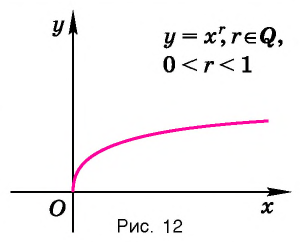
где 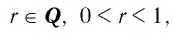 те же, что и у функции
те же, что и у функции 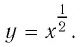 (Сформулируйте эти свойства, пользуясь рисунком 12.)
(Сформулируйте эти свойства, пользуясь рисунком 12.)
Подчеркнем, что функция 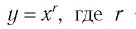 — положительное рациональное, но не натуральное число, рассматривается только на множестве всех неотрицательных действительных чисел.
— положительное рациональное, но не натуральное число, рассматривается только на множестве всех неотрицательных действительных чисел.
Пример №8
Изобразить (схематично) график функции:
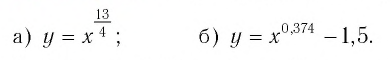
Решение:
а) На рисунке 13, 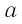 схематично изображен график функции
схематично изображен график функции 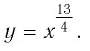
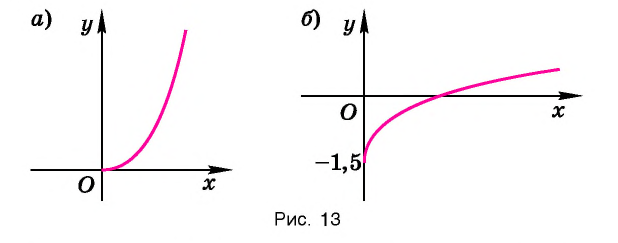
б) На рисунке 13, б схематично изображен график функции 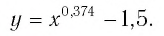
1. Сформулируйте свойства функции 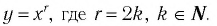
2. Сформулируйте свойства функции 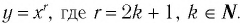
3. Сформулируйте свойства функции 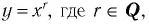 если:
если: 
4. Изобразите схематично график функции 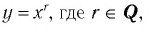 если:
если:

5. Что можно сказать об особенностях графика:
а) четной функции;
б) нечетной функции;
в) периодической функции?
6. Что можно сказать об особенностях области определения:
а) четной функции;
б) нечетной функции;
в) периодической функции?
Степенная функция (показатель отрицательный)
Вы изучали функцию 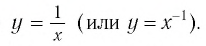 Эта функция является частным случаем степенной функции
Эта функция является частным случаем степенной функции 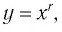 где
где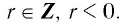
Рассмотрим еще несколько случаев степенной функции с отрицательным показателем:
Функция y=xr, где r=-2k+1, k∈N
1. Функция 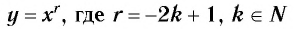
Естественная область определения выражения 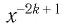 — множество всех действительных чисел, кроме нуля, т. е.
— множество всех действительных чисел, кроме нуля, т. е. 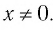 Другими словами, областью определения функции
Другими словами, областью определения функции 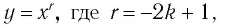
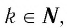 будет множество
будет множество 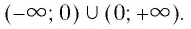
Назовем свойства функции 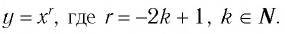 Они те же, что и у функции
Они те же, что и у функции 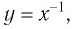 и устанавливаются так же, как свойства этой функции. Для сравнения графики функций
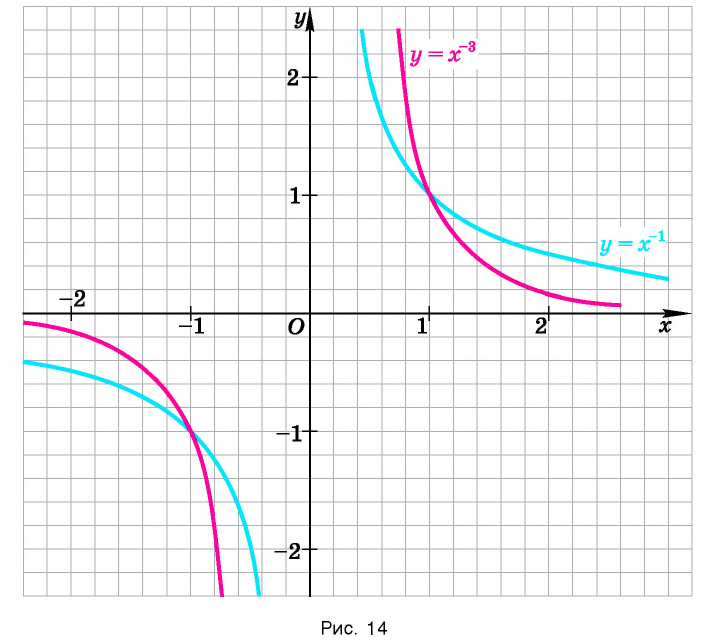
и устанавливаются так же, как свойства этой функции. Для сравнения графики функций 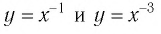 изображены на рисунке (рис. 14).
изображены на рисунке (рис. 14).
Теорема (о свойствах функции 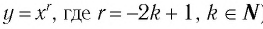 )
)
- Областью определения функции является множество всех действительных чисел, кроме нуля, т. е.
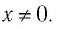
- Множеством (областью) значений функции является множество всех действительных чисел, кроме нуля, т. е.
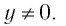
- Наименьшего и наибольшего значений функция не имеет.
- График функции не пересекает координатных осей.
- Функция не имеет нулей.
- Функция принимает отрицательные значения (у < 0) на промежутке
 и принимает положительные значения (у > 0) на промежутке
и принимает положительные значения (у > 0) на промежутке 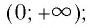 т.е. график функции расположен в I и III координатных углах.
т.е. график функции расположен в I и III координатных углах. - Функция нечетная; график функции симметричен относительно начала координат.
- Функция является убывающей на промежутке
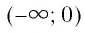 и убывающей на промежутке
и убывающей на промежутке 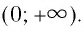
- Функция не является периодической.
В справедливости этих свойств убедитесь, используя схематичное изображение графика функции 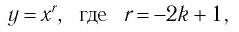
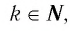 на рисунке 15.
на рисунке 15.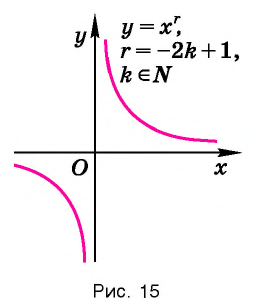
Заметим, что утверждение функция 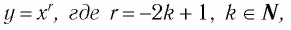 убывает на всей области определения — неверно (поясните почему).
убывает на всей области определения — неверно (поясните почему).
Функция y=xr, где r=-2k, k∈N
2. Функция 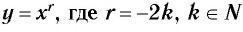
Естественная область определения выражения 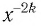 — множество всех действительных чисел, кроме нуля, т. е.
— множество всех действительных чисел, кроме нуля, т. е. 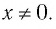 Другими словами, областью определения функции
Другими словами, областью определения функции 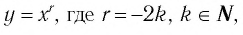 будет множество
будет множество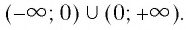
Назовем свойства функции 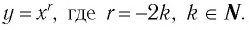 Они устанавливаются так же, как свойства функции
Они устанавливаются так же, как свойства функции 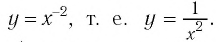 Для сравнения графики функций
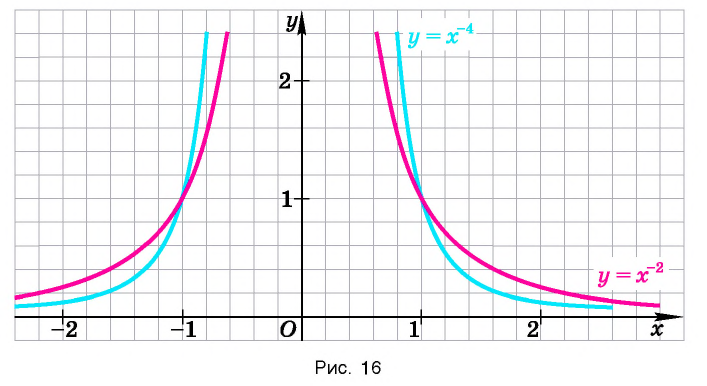
Для сравнения графики функций 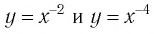 изображены на рисунке 16.
изображены на рисунке 16.
Теорема (о свойствах функции 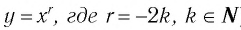 )
)
1. Областью определения функции является множество всех действительных чисел, кроме нуля, т. е.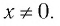
2. Множеством (областью) значений функции является промежуток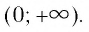
3. Наименьшего и наибольшего значений функция не имеет.
4. График функции не пересекает координатных осей.
5. Функция не имеет нулей.
6. Функция принимает положительные значения (у > 0) на всей области определения 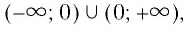 т. е. график функции расположен в
т. е. график функции расположен в 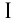 и
и 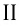 координатных углах.
координатных углах.
7. Функция четная; график функции симметричен относительно оси ординат.
8. Функция возрастающая на промежутке 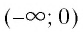 и убывающая на промежутке
и убывающая на промежутке 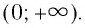
9. Функция не является периодической.
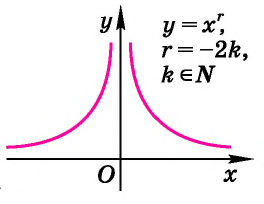
Убедитесь в справедливости свойств, используя схематичное изображение графика функции 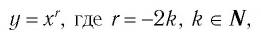 на рисунке 17.
на рисунке 17.
Пример №9
Сравнив изображения графиков функций 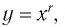 где
где 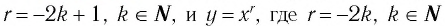 (см. рис. 15, 17), указать, на каком из множеств обе функции:
(см. рис. 15, 17), указать, на каком из множеств обе функции:
а) возрастают;
б) имеют значения разных знаков;
в) убывают;
г) принимают положительные значения;
д) принимают равные значения.
Ответ: 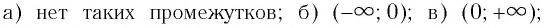
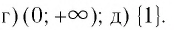
Функция y=xr, где r - отрицательное рациональное нецелое число
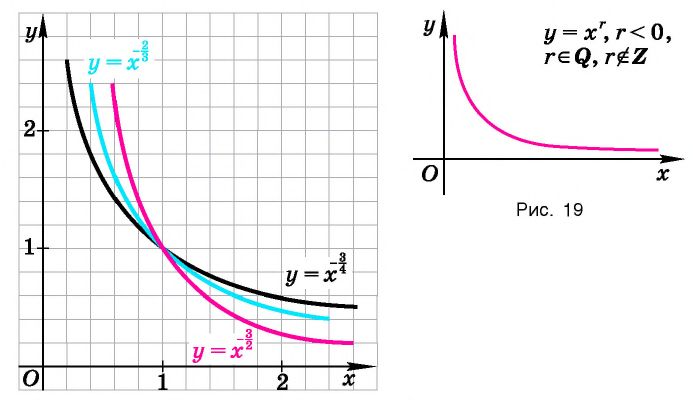
3. Функция 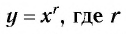 — отрицательное рациональное нецелое число, т. е.
— отрицательное рациональное нецелое число, т. е. 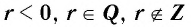
Область определения этой функции — промежуток 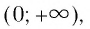 т. е. эта функция рассматривается только на множестве всех положительных действительных чисел.
т. е. эта функция рассматривается только на множестве всех положительных действительных чисел.
Для сравнения графики функций 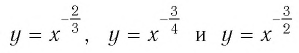 изображены на рисунке 18.
изображены на рисунке 18.
Свойства функции 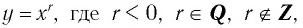 те же, что и свойства функции
те же, что и свойства функции 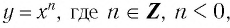 рассматриваемой на промежутке
рассматриваемой на промежутке 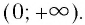
Вычисление степеней с рациональным показателем
Допустим, что равенство 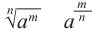 (здесь
(здесь 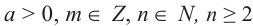 ) верно и в случае, если
) верно и в случае, если 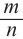 дробное число. Тогда все свойства степени с целым показателем выполняются и для степеней с дробным показателем при положительном основании.
дробное число. Тогда все свойства степени с целым показателем выполняются и для степеней с дробным показателем при положительном основании.
Определение: Если 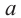 - положительное число, а
- положительное число, а 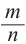 — дробное число (здесь
— дробное число (здесь 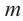 - целое,
- целое, 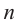 - натуральное число,
- натуральное число, 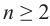 ), то
), то 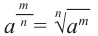
Пример: 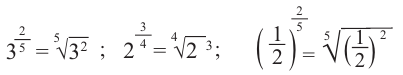
Т.к 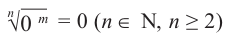 при
при 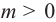 , то при
, то при 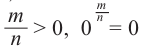 . Степень с дробным показателем для отрицательного числа не рассматривается. Например, выражение
. Степень с дробным показателем для отрицательного числа не рассматривается. Например, выражение 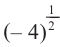 не имеет смысла.
не имеет смысла.
Свойства степени с рациональным показателем
Известные нам свойства степени с целым показателем справедливы и для степеней с любым рациональным показателем при положительном действительном основании.

Здесь 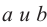 положительные действительные числа,
положительные действительные числа, 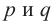 рациональные.
рациональные.
Докажите, что 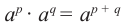 , если
, если 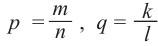 (
(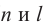 - натуральные числа,
- натуральные числа, 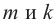 - целые числа).
- целые числа).
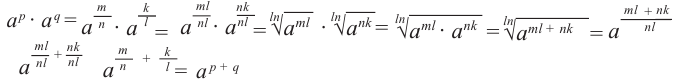
Остальные свойства доказываются аналогичным способом.
Пример: Выразите переменную 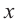 через
через 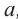 если
если 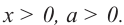
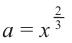
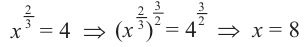
| Рекомендую подробно изучить предметы: |
| Ещё лекции с примерами решения и объяснением: |