
Степень с действительным показателем с примерами решения
Содержание:
Понятие степени 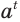
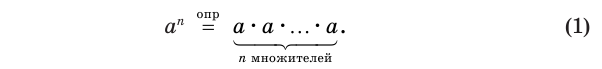
Здесь символом 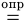 подчеркивается, что равенство (1) особое: это равенство-определение, и поэтому не требует обоснования в отличие, например, от равенства
подчеркивается, что равенство (1) особое: это равенство-определение, и поэтому не требует обоснования в отличие, например, от равенства  .
.
Определение-равенство (1) осмысленное только для тех натуральных значений показателя 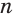 , которые не меньше 2, так как умножение есть двуместное действие. Поэтому натуральная степень
, которые не меньше 2, так как умножение есть двуместное действие. Поэтому натуральная степень 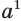 требует особого определения, но такого, при котором сохраняются свойства натуральной степени, в частности, свойство
требует особого определения, но такого, при котором сохраняются свойства натуральной степени, в частности, свойство 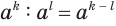 . С учетом этого должно быть:
. С учетом этого должно быть: 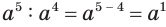 . Вместе с этим
. Вместе с этим 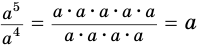 . Поэтому первую степень
. Поэтому первую степень 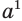 целесообразно определить так:
целесообразно определить так:

Так же, поскольку 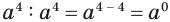 и вместе с этим
и вместе с этим 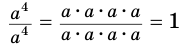 , то нулевую степень
, то нулевую степень 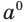 целесообразно определить так:
целесообразно определить так:

Обратив внимание, например, на то, что 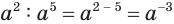 и вместе с этим
и вместе с этим 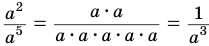 приходим к выводу, что отрицательную целую степень
приходим к выводу, что отрицательную целую степень 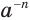 , где
, где 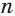 — натуральное число, целесообразно определить так:
— натуральное число, целесообразно определить так:

При этом, если в равенствах (1) и (2) основание 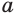 может иметь любое действительное значение, то в равенствах (3) и (4) это значение должно быть отличным от нуля.
может иметь любое действительное значение, то в равенствах (3) и (4) это значение должно быть отличным от нуля.
Рациональную степень 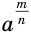 с положительным основанием
с положительным основанием 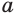 введем из следующих соображений. Для целых показателей
введем из следующих соображений. Для целых показателей 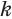 и
и 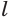 выполняется свойство
выполняется свойство 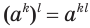 . Желательно, чтобы оно выполнялось и для дробных показателей. В таком случае будет
. Желательно, чтобы оно выполнялось и для дробных показателей. В таком случае будет 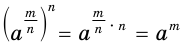 . Но равенство
. Но равенство 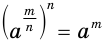 означает, что число
означает, что число 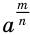 должно быть корнем
должно быть корнем 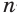 -й степени из числа
-й степени из числа 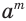 :
:

Примеры:
С учетом определения (5) получим:
а) 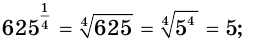
б) 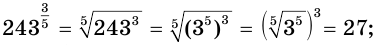
в) 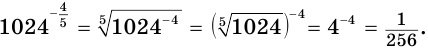
Из определения степени с рациональным показателем следует, что при любом положительном значении основания а и любом рациональном значении показателя 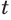 число
число 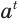 является положительным.
является положительным.
Поскольку, с учетом свойств корня, 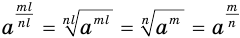 , то значение рациональной степени а' не зависит от того, какой дробью из множества равных дробей представлен рациональный показатель
, то значение рациональной степени а' не зависит от того, какой дробью из множества равных дробей представлен рациональный показатель 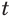 .
.
Если показателем степени является дробь 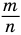 с нечетным знаменателем
с нечетным знаменателем 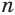 , определение (5) распространяется и на отрицательные значения основания
, определение (5) распространяется и на отрицательные значения основания 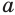 .
.
Пример:
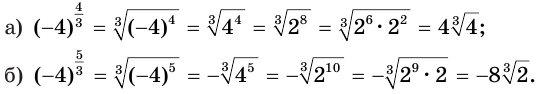
Если показателем степени является дробь 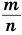 с четным знаменателем
с четным знаменателем 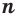 , то степень
, то степень 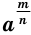 с отрицательным основанием не определяется.
с отрицательным основанием не определяется.
Степень 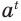 положительного числа
положительного числа 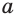 с иррациональным показателем
с иррациональным показателем 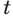 определяется так.
определяется так.
Пусть 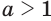 . Для числа
. Для числа 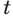 выпишем последовательности
выпишем последовательности
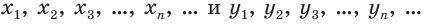
его десятичных приближений по недостатку и по избытку соответственно. Тогда
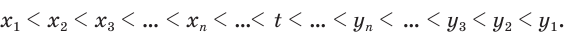
Из этих неравенств с учетом того, что если 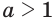 и
и 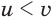 , то
, то 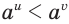 , получим:
, получим:
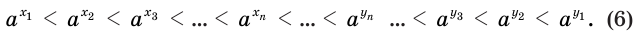
Оценим разность 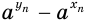 . Получим:
. Получим:
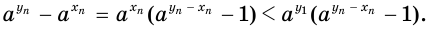
Если значение переменной  неограниченно увеличивается, то значение выражения
неограниченно увеличивается, то значение выражения  стремится к нулю, значение выражения
стремится к нулю, значение выражения 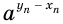 — к единице, а значение выражения
— к единице, а значение выражения 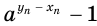 , а потому и выражения
, а потому и выражения 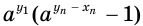 — к нулю. Это означает, что значения выражений
— к нулю. Это означает, что значения выражений 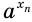 и
и 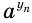 приближаются друг к другу. Можно доказать, что есть только одно число
приближаются друг к другу. Можно доказать, что есть только одно число 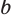 , для которого
, для которого 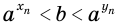 при всех
при всех 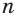 . Оно и принимается в качестве значения иррациональной степени
. Оно и принимается в качестве значения иррациональной степени 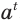 .
.
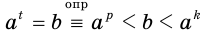 , где
, где 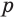 и
и 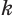 — рациональные приближения иррационального числа
— рациональные приближения иррационального числа 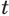 по недостатку и по избытку соответственно.
по недостатку и по избытку соответственно.
Так же определяется иррациональная степень 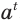 для
для 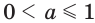 . При этом для любого действительного показателя
. При этом для любого действительного показателя 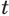

Отметим, что если действительный показатель 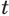 больше нуля, то
больше нуля, то 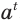 имеет смысл и при
имеет смысл и при 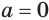 , именно:
, именно:
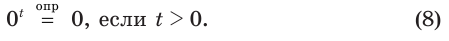
Пример:
Рассмотрим иррациональную степень 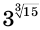 . Учитывая, что
. Учитывая, что
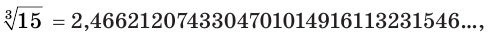
получим:
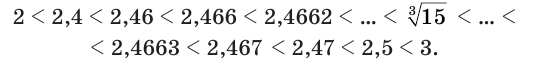
Поэтому

или
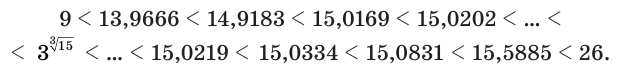
Вычисление на калькуляторе для числа 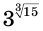 дает:
дает:
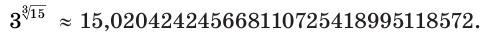
Для степени с действительным показателем верны известные вам основные свойства степени:
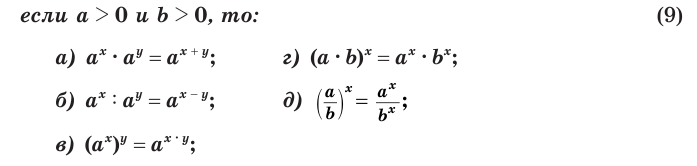
- если
 , то выражение
, то выражение 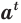 имеет значение при любом значении переменной
имеет значение при любом значении переменной 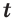 ; (10)
; (10) - если
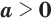 , то
, то 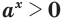 при любом значении переменной
при любом значении переменной 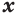 ; (11)
; (11) - если
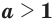 , то
, то 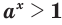 при
при 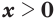 и
и 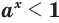 при
при 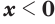 ; (12)
; (12) - если
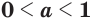 , то
, то 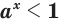 при
при 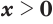 и
и 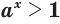 при
при 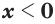 ; (13)
; (13) - если
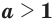 и
и 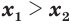 , то
, то 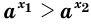 ; (14)
; (14) - если
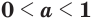 и
и 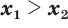 , то
, то 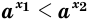 . (15)
. (15)
Докажем, например, что 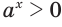 при любом иррациональном значении переменной
при любом иррациональном значении переменной 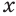 .
.
Если 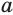 = 1, то
= 1, то 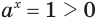 .
.
Пусть 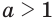 ,
, 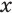 — иррациональное число,
— иррациональное число, 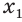 и
и 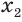 — рациональные приближения к
— рациональные приближения к 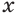 по недостатку и избытку:
по недостатку и избытку: 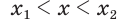 . Из определения иррациональной степени следует, что
. Из определения иррациональной степени следует, что 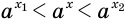 , а поскольку
, а поскольку 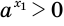 , то и
, то и 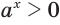 .
.
Если 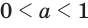 , то так же получим, что
, то так же получим, что 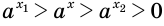 .
.
Понятием степени с натуральным показателем пользовались уже в Древней Греции. Об этом свидетельствуют термины квадрат числа и куб числа, известные с тех времен. Современные обозначения натуральной степени 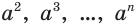 ввел в 1637 г. французский математик Рене Декарт. Французский математик Николя Орем (около 1323—1382) уже пользовался дробными показателями. Отрицательные и нулевой показатели ввел в обиход французский математик Николя Шюке (около 1445 — около 1500). Нидерландский ученый и инженер Симон Стевин (1548—1620) обратил внимание на то, что
ввел в 1637 г. французский математик Рене Декарт. Французский математик Николя Орем (около 1323—1382) уже пользовался дробными показателями. Отрицательные и нулевой показатели ввел в обиход французский математик Николя Шюке (около 1445 — около 1500). Нидерландский ученый и инженер Симон Стевин (1548—1620) обратил внимание на то, что 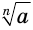 целесообразно понимать как
целесообразно понимать как 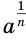 . Знак
. Знак 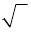 для обозначения корня впервые использовал в 1525 г. чешский математик Криштян Рудольф (около 1500 — около 1545), а современный символ
для обозначения корня впервые использовал в 1525 г. чешский математик Криштян Рудольф (около 1500 — около 1545), а современный символ 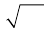 с горизонтальной чертой сверху ввел Декарт.
с горизонтальной чертой сверху ввел Декарт.
Степенная функция с действительным показателем
Выражение 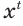 , в котором переменные
, в котором переменные 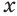 и
и 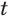 могут принимать разные действительные значения, описывает разные функции в зависимости от того, значение какой переменной —
могут принимать разные действительные значения, описывает разные функции в зависимости от того, значение какой переменной — 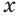 или
или 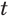 — сделать неизменным, постоянным.
— сделать неизменным, постоянным.
Если зафиксировать значение переменной 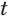 , т. е. придать этой переменной определенное числовое значение
, т. е. придать этой переменной определенное числовое значение 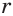 , то выражение
, то выражение 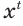 задает степенную функцию
задает степенную функцию 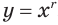 .
.
Если зафиксировать значение переменной 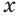 , т. е. придать ей определенное числовое значение
, т. е. придать ей определенное числовое значение 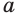 , то выражение
, то выражение 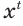 задает показательную функцию
задает показательную функцию 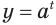 .
.
В этом параграфе рассмотрим степенную функцию, т. е. функцию вида 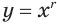 , где
, где 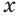 — аргумент, a
— аргумент, a 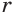 — некоторое действительное число.
— некоторое действительное число.
Все степенные функции определены при положительных значениях аргумента. При некоторых показателях 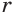 область определения степенной функции
область определения степенной функции 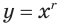 более широкая. Например, степенные функции
более широкая. Например, степенные функции 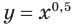 и
и 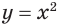 своими областями определения имеют соответственно множество всех неотрицательных действительных чисел и всех действительных чисел.
своими областями определения имеют соответственно множество всех неотрицательных действительных чисел и всех действительных чисел.
Рассмотрим сначала степенную функцию 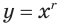 при
при 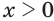 . При положительных значениях аргумента ее значениями являются все положительные действительные числа. Ряд свойств степенной функции
. При положительных значениях аргумента ее значениями являются все положительные действительные числа. Ряд свойств степенной функции 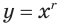 и ход ее графика зависят от значения показателя
и ход ее графика зависят от значения показателя 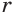 .
.
Если  , то свойства степенной функции похожи на свойства функции
, то свойства степенной функции похожи на свойства функции 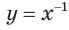 (рис. 64).
(рис. 64).
При 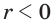 степенная функция
степенная функция 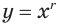 :
:
- убывает от
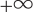 до 0;
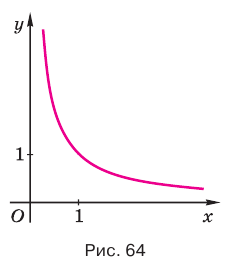
до 0; - выпукла вниз, т. е. часть ее графика, ограниченного любыми двумя его точками, расположена ниже отрезка, который эти точки соединяет (рис. 65).
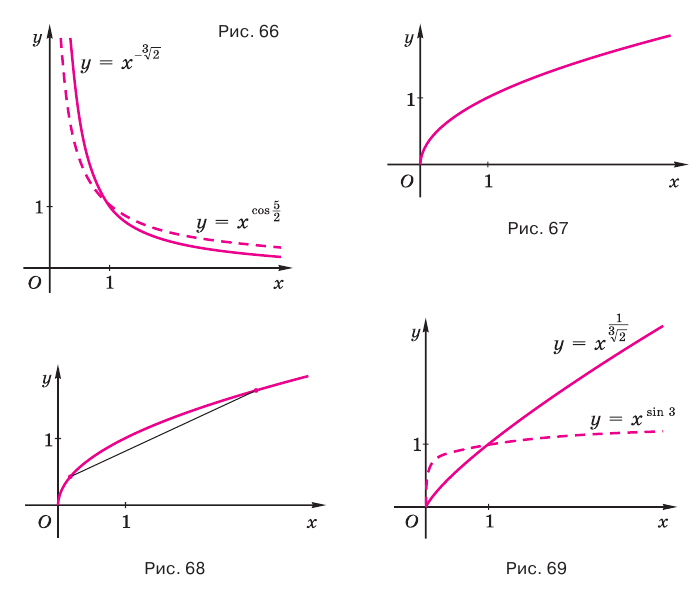
На рисунке 66 показаны графики степенных функций 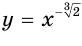 и
и 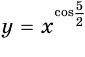 с отрицательными показателями
с отрицательными показателями 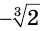 и
и 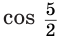 , которые соответственно приближенно равны -1,26 и -0,801.
, которые соответственно приближенно равны -1,26 и -0,801.
Если 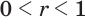 , то свойства степенной функции похожи на свойства функции
, то свойства степенной функции похожи на свойства функции 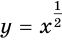 (рис. 67).
(рис. 67).
При 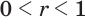 степенная функция
степенная функция 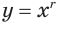 :
:
- возрастает от 0 до
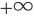 ;
; - выпукла вверх, т. е. часть ее графика, ограниченного любыми двумя его точками, расположена выше отрезка, который эти точки соединяет (рис. 68).
На рисунке 69 показаны графики функций 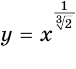 и
и 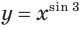 с положительными меньшими единицы показателями
с положительными меньшими единицы показателями 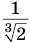 и sin 3, которые соответственно приближенно равны 0,79 и 0,14.
и sin 3, которые соответственно приближенно равны 0,79 и 0,14.
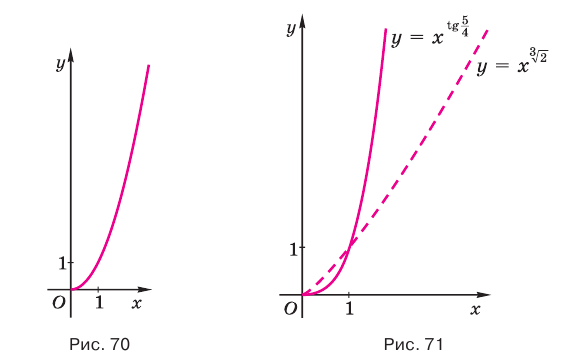
Если  , то свойства степенной функции похожи на свойства функции
, то свойства степенной функции похожи на свойства функции 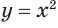 (рис. 70).
(рис. 70).
При 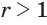 степенная функция
степенная функция 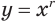 :
:
- возрастает от 0 до
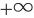 ;
; - выпукла вниз.
На рисунке 71 показаны графики функций 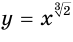 и
и 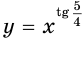 с положительными большими единицы показателями
с положительными большими единицы показателями 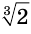 и
и 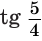 , которые соответственно приближенно равны 1,26 и 3,01.
, которые соответственно приближенно равны 1,26 и 3,01.
При положительных показателях степени в область определения функции включается и число 0, поскольку при 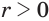 верно равенство
верно равенство 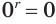 .
.
Если показатель 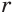 степени
степени 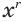 есть рациональное число
есть рациональное число 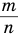 , где
, где 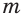 — целое число,
— целое число, 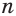 — нечетное натуральное число и числа
— нечетное натуральное число и числа 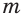 и
и 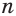 взаимно просты, степенная функция
взаимно просты, степенная функция 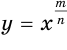 , т. е. функция
, т. е. функция 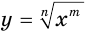 , может быть распространена и на отрицательные значения аргумента
, может быть распространена и на отрицательные значения аргумента 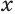 , так как в этом случае выражение
, так как в этом случае выражение 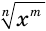 имеет значения при всех значениях переменной
имеет значения при всех значениях переменной 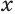 .
.
При этом, если 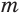 — нечетное число, то
— нечетное число, то 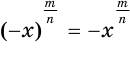 , а если
, а если 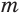 — четное число, то
— четное число, то 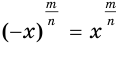 . Это означает, что при нечетных значениях числителя
. Это означает, что при нечетных значениях числителя 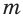 функция
функция 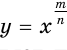 нечетная, а при четных — четная. Отмеченное позволяет получить график функции
нечетная, а при четных — четная. Отмеченное позволяет получить график функции 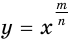 при отрицательных значениях аргумента симметричным отображением графика функции при
при отрицательных значениях аргумента симметричным отображением графика функции при 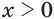 относительно начала координат или оси ординат при нечетных и при четных значениях числителя
относительно начала координат или оси ординат при нечетных и при четных значениях числителя 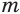 соответственно.
соответственно.
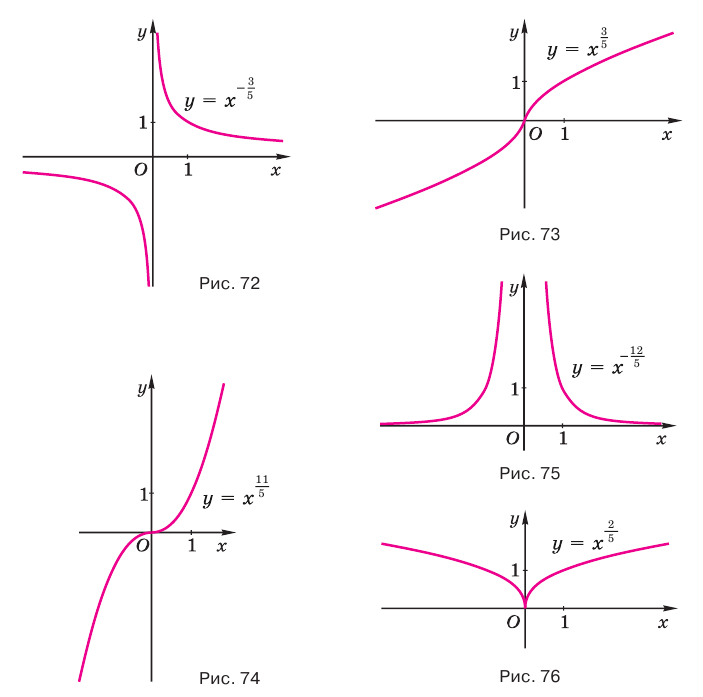
На рисунках 72, 73 и 74 показаны графики функций 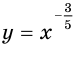 ,
, 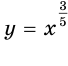 и
и 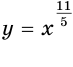 с нечетными значениями числителя
с нечетными значениями числителя  , а на рисунках 75, 76 и 77 — графики функций
, а на рисунках 75, 76 и 77 — графики функций 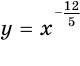 ,
, 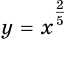 и
и 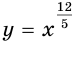 с четными значениями числителя
с четными значениями числителя  .
.
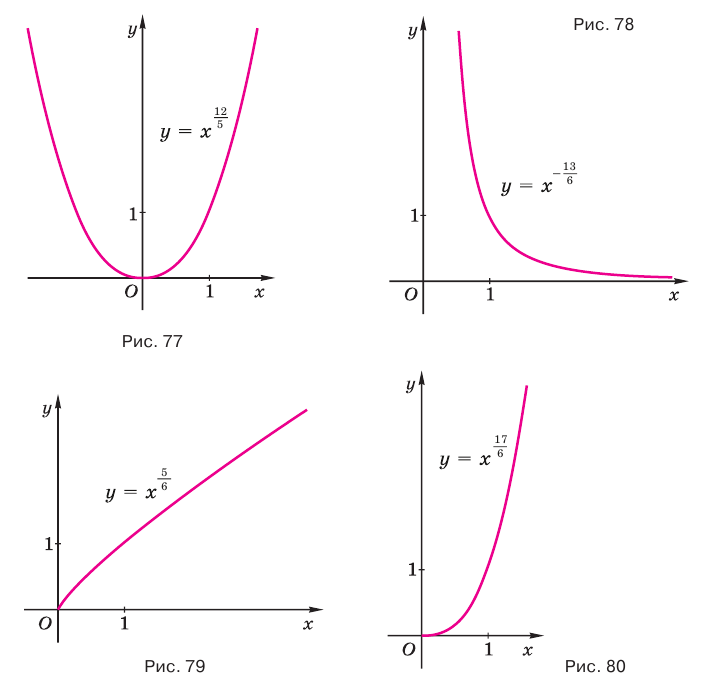
Если знаменатель 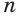 — четное натуральное число, то числитель
— четное натуральное число, то числитель 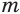 может быть только нечетным, так как в противном случае дробь
может быть только нечетным, так как в противном случае дробь 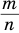 будет сократимой. Учитывая, что выражение
будет сократимой. Учитывая, что выражение 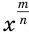 , т.е. выражение
, т.е. выражение 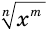 , имеет значения только если
, имеет значения только если 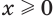 при
при 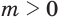 и
и 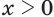 при
при 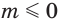 , получаем, что при четном значении знаменателя
, получаем, что при четном значении знаменателя 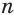 функция
функция 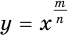 не распространяется на отрицательные значения аргумента. На рисунках 78, 79 и 80 показаны графики функций
не распространяется на отрицательные значения аргумента. На рисунках 78, 79 и 80 показаны графики функций 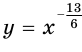 ,
, 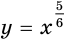 и
и 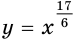 .
.
Раньше было доказано, что производная 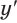 степенной функции
степенной функции 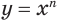 для целого показателя
для целого показателя 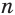 определяется формулой
определяется формулой 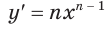 . Можно доказать, что по этой же формуле можно находить производную степенной функции при любом действительном показателе:
. Можно доказать, что по этой же формуле можно находить производную степенной функции при любом действительном показателе:
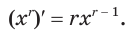
Всё о степени с действительным показателем
Мы уже знаем, что такое степень с рациональным показателем. Теперь определим степень с иррациональным показателем при основании 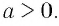 Сделаем это сначала для основания
Сделаем это сначала для основания 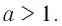
Пусть s — иррациональное число. Возьмем такие рациональные числа 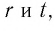 что
что 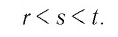
Тогда по свойству степени с рациональным показателем 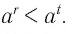 Будет естественно определить степень
Будет естественно определить степень 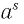 так, чтобы это число удовлетворяло неравенству
так, чтобы это число удовлетворяло неравенству
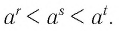
Именно так мы и поступим.
Определение:
Пусть 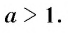 Степенью числа
Степенью числа 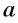 с иррациональным показателем
с иррациональным показателем 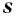 называется такое число
называется такое число 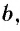 что
что
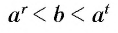
при любых рациональных значениях 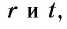 удовлетворяющих неравенству
удовлетворяющих неравенству
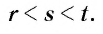
Это число 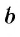 обозначается
обозначается 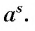
Утверждение о существовании и единственности такого числа 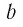 мы примем без доказательства.
мы примем без доказательства.
Аналогично для положительного числа 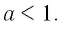
Определение:
Пусть 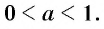 Степенью числа
Степенью числа 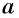 с иррациональным показателем
с иррациональным показателем 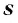 называется такое число
называется такое число 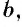 что
что
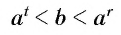
при любых рациональных значениях 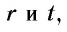 удовлетворяющих неравенству
удовлетворяющих неравенству
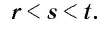
Это число 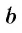 обозначается
обозначается 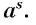
Утверждение о существовании и единственности такого числа 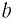 мы примем без доказательства.
мы примем без доказательства.
Наконец определим степень с основанием 1.
Определение:
Для любого иррационального числа 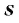
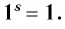
Таким образом, при положительном основании понятие степени определено для любого рационального и для любого иррационального показателя, т. е. для любого действительного показателя. При этом все действия со степенями с произвольными действительными показателями обладают теми же свойствами, что и действия со степенями с рациональными показателями. Эти свойства мы сформулируем в следующей теореме, которую примем без доказательства.
Теорема:
Для любых значений 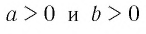 при любых действительных
при любых действительных 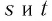 верны равенства:
верны равенства:
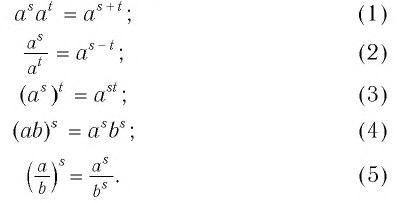
Пример №1
Расположить в порядке убывания числа:

Решение:
а) Сравним числа 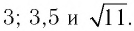 Поскольку
Поскольку 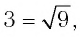
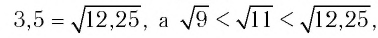 то
то
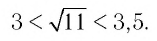
Значит, по определению степени с иррациональным показателем при основании 0,63 получим верное неравенство
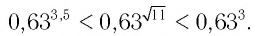
б) Сравним числа 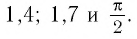 Поскольку
Поскольку 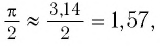 то
то
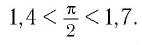
Значит, по определению степени с иррациональным показателем при основании 11,7 получим верное неравенство
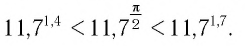
Ответ: 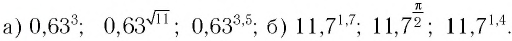
Пример №2
Пользуясь определением степени с иррациональным показателем, записать по три верных двойных неравенства для степени 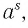 если:
если: 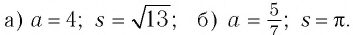
Решение:
а) Запишем три верных двойных неравенства сначала для показателя 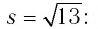
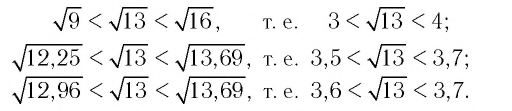
По определению степени с иррациональным показателем при основании 4 > 1 будут верны и неравенства
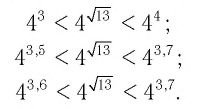
б) Запишем три верных двойных неравенства сначала для показателя 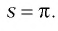 Так как
Так как 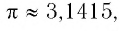 то имеем
то имеем
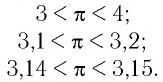
По определению степени с иррациональным показателем при основании 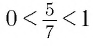 будут верными и неравенства
будут верными и неравенства
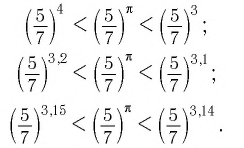
Определение степени с действительными показателями
Вспомните, как постепенно расширялось понятие степени. Сначала вводилось понятие степени числа с натуральным показателем 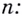

Затем рассматривались степени с целым показателем:
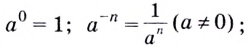
наконец — с произвольным рациональным показателем степени:
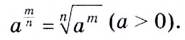
Математики часто используют также степени с произвольными действительными показателями. Множество действительных чисел состоит из чисел рациональных и иррациональных. Что такое степень с рациональным показателям, вы уже знаете. Введём понятие степени с иррациональным показателем.
Пусть
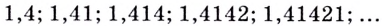
бесконечная последовательность рациональных приближений числа 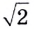 с точностью до десятых, сотых, тысячных и т. д. То есть это последовательность рациональных чисел, достаточно близко приближающихся к
с точностью до десятых, сотых, тысячных и т. д. То есть это последовательность рациональных чисел, достаточно близко приближающихся к 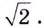
Тогда
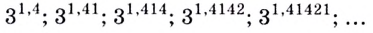
последовательность чисел (степеней с рациональными показателями), которые как угодно близко приближаются к некоторому действительному числу. Это действительное число и принято считать значением степени 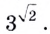
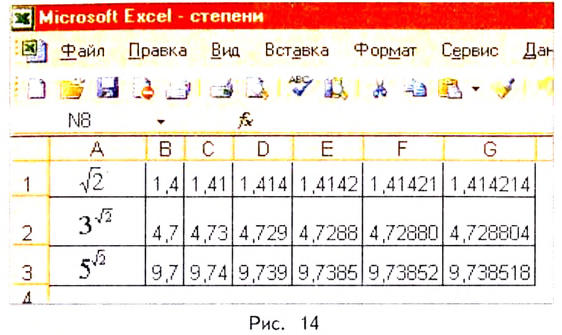
Приближённые значения (с точностью до десятых, сотых, тысячных и т. д.) для степеней  представлены в таблице, выполненной с помощью программы Excel (рис. 14).
представлены в таблице, выполненной с помощью программы Excel (рис. 14).
Замечание: Приведённое выше объяснение понятия степени с иррациональным показателем с точки зрения математики не совсем корректное, поскольку в нём используется не математическое понятие «близко подходит». В математике ему соответствует понятие предел последовательности. Число  называют пределом бесконечной последовательности
называют пределом бесконечной последовательности 
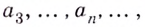 если для любого положительного числа
если для любого положительного числа 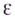 найдётся такое натуральное число
найдётся такое натуральное число 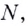 что для всех
что для всех 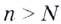 выполняется неравенство
выполняется неравенство 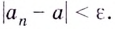 Поэтому правильнее было бы сказать, что если пределом последовательности
Поэтому правильнее было бы сказать, что если пределом последовательности 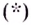 есть число
есть число 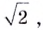 то пределом последовательности
то пределом последовательности  является число
является число 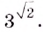 Вообще, если
Вообще, если  — число действительное, а
— число действительное, а 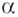 — иррациональное, то под степенью
— иррациональное, то под степенью 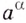 понимают предел бесконечной последовательности
понимают предел бесконечной последовательности 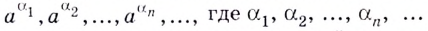 — бесконечная последовательность, пределом которой является число Корректность такого определения обоснована в строгих курсах математического анализа.
— бесконечная последовательность, пределом которой является число Корректность такого определения обоснована в строгих курсах математического анализа.
Какими бы ни были действительные числа 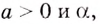 степень
степень 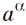 всегда имеет смысл, т. е. равна некоторому действительному числу. Для таких степеней выполняются свойства:
всегда имеет смысл, т. е. равна некоторому действительному числу. Для таких степеней выполняются свойства:
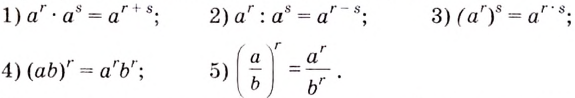
Выражения, содержащие степени с действительными показателями, можно преобразовывать так же, как выражения со степенями с рациональными показателями.
Пример:
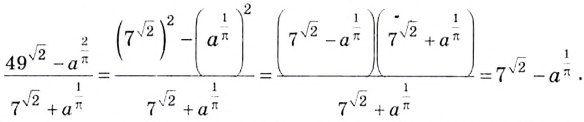
Как вы уже знаете, степени с дробными показателями рассматривают только при условии, что их основания — числа положительные. И степени с иррациональными показателями рассматривают только при условии, что основания степеней — числа положительные. А, например, выражения 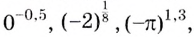
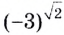 не имеют смысла. Это записи, которые не обозначают никаких чисел. Но, если
не имеют смысла. Это записи, которые не обозначают никаких чисел. Но, если 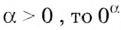 существует и
существует и 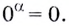
Зная только степени с рациональными показателями, вы раньше и степенные функции рассматривали не все, а только такие, показатели степеней которых были рациональными числами. Теперь понятие степенной функции можно расширить. Степенной далее будем называть функцию 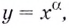 где
где 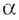 — произвольное действительное число. В частности, функции
— произвольное действительное число. В частности, функции 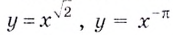 степенные. Свойства этих функций такие же, как и свойства степенных функций с рациональными показателями степеней.
степенные. Свойства этих функций такие же, как и свойства степенных функций с рациональными показателями степеней.
При каждом действительном 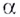 степенная функция
степенная функция 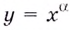 определена на промежутке
определена на промежутке 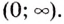 Свойства таких функций указаны в таблице.
Свойства таких функций указаны в таблице.
Свойства степенной функции 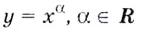

Если 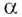 — положительное иррациональное число, функция
— положительное иррациональное число, функция 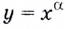 определена на промежутке
определена на промежутке 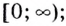 такое же и множество её значений. Если иррациональное число
такое же и множество её значений. Если иррациональное число 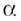 отрицательное, то областью определения и областью значений функции
отрицательное, то областью определения и областью значений функции 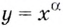 является промежуток
является промежуток 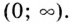 Несколько графиков таких функций изображены на рисунках 15, 16.
Несколько графиков таких функций изображены на рисунках 15, 16.
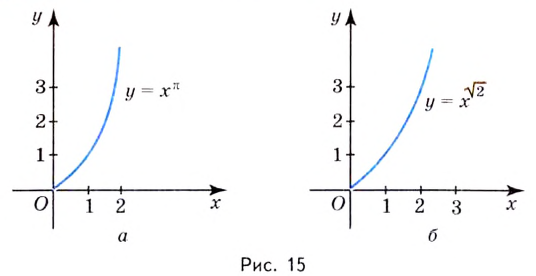
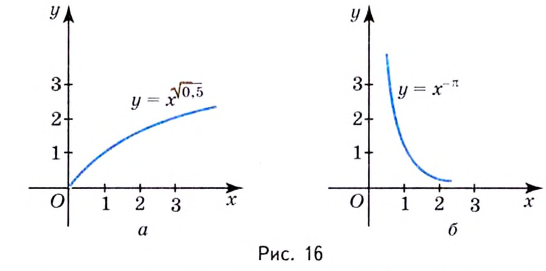
Для отдельных значений 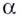 степенная функция может рассматриваться и на более широкой области определения. В частности при натуральных
степенная функция может рассматриваться и на более широкой области определения. В частности при натуральных 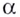 она определена на
она определена на 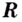 (рис. 17, а), а при целых отрицательных — на множестве
(рис. 17, а), а при целых отрицательных — на множестве 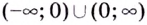 (рис. 17, б). В этих случаях при чётных значениях
(рис. 17, б). В этих случаях при чётных значениях 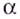 функция
функция 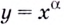 чётная, а при нечётных
чётная, а при нечётных 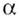 — нечётная.
— нечётная.
Пример №3
Проходит ли график функции 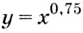 через точку
через точку 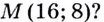
Решение:
Если 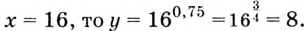
Ответ. Проходит.
Пример №4
Известно, что график функции 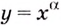 проходит через точку
проходит через точку 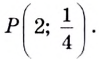 Чему равно
Чему равно 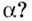
Решение:
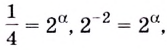 отсюда
отсюда 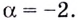
Ответ. -2.
Пример №5
Упростите выражение 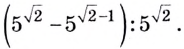
Решение:
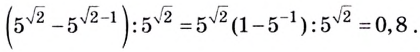
Ответ. 0,8.
Пример №6
Сравните числа: 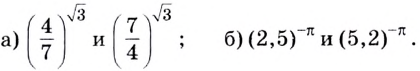
Решение:
а) Функция 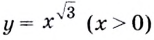 — возрастающая, так как
— возрастающая, так как 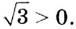 Поскольку
Поскольку 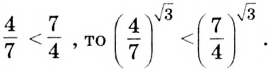
б) Функция 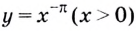 — убывающая, так как -
— убывающая, так как -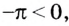 поэтому
поэтому 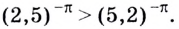
| Рекомендую подробно изучить предметы: |
| Ещё лекции с примерами решения и объяснением: |