Статистическая проверка гипотез - определение и вычисление с примерами решения

Содержание:

Основы математической статистики:

Математическая статистика изучает математические методы систематизации, обработки и использования статистических данных для научных и практических выводов о природе исследуемого явления.

Предмет, метод и основные задачи математической статистики

Статистическое описание совокупности объектов занимает промежуточное состояние между индивидуальным описанием каждого из объектов совокупности и описанием самой совокупности по её общим свойствам. Статистический метод сводится к подсчету объектов, входящих в те или иные группы, рассмотрению распределения количественных признаков, применению выборочного метода, использованию теории вероятностей при достаточно большом числе наблюдений. Сущность статистического метода определяет предмет математической статистики. Математическая статистика в основном решает три основные задачи:

1. оценка на основе наблюдений неизвестной статистической функции распределений;
2. оценка неизвестных параметров распределения;
3. выдвижение и проверка cтатистических гипотез.

Статистический ряд

Пусть проводится исследование совокупности однородных объектов, которые характеризуются качественным или количественным признаком X. Например, имеется партия деталей. Качественным признаком является стандартность детали, а количественным - например, их длина. При статистическом изучении большого количества объектов, чаще всего, из общего множества объектов выбирают их ограниченное количество, которое наиболее полно описывает свойства всего множества объектов.

Определение: Вся совокупность объектов, подлежащая изучению, называется генеральной совокупностью.

Определение: Ограниченная часть объектов, наиболее полно характеризующая свойства генеральной совокупности, называется выборочной совокупностью.

Определение: Число объектов в генеральной и выборочной совокупностях называется объёмом выборки.

Выборочный метод состоит в том, что после проведения серии независимых испытаний (опыты независимы в смысле теории вероятностей) из генеральной совокупности объёмом N берется выборка объемом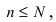

Пусть над случайной величиной X проводится серия независимых испытаний, в каждом из которых случайная величина X принимает определенное значение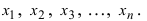

Определение: Совокупность результатов наблюдений называется простой статистической совокупностью.

Если случайная величина X принимает 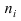раз значение 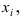то объём выборки равен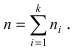

Определение: Ряд значений 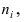расположенные в порядке возрастания значений, называется вариационным рядом (упорядоченной выборкой), значения х, называются вариантами, а числа 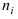- их частотами.

Определение: Числа 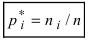называются относительными частотами.

Определение: Разность между наибольшим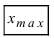и наименьшим 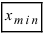значениями в выборке называется размахом варьирования или широтой распределения выборки, т.е.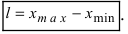

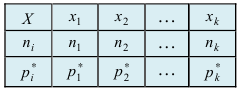
Определение: Перечень вариант и соответствующих им частот (или относительных частот) называют статистическим распределением выборки.

Если число опытов достаточно велико и случайная величина X непрерывна, то весь диапазон значений случайной величиной X разбивают на интервалы 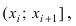которые располагают в порядке возрастания. Подсчитывают количество значений случайной величиной X, которые попали в этот интервал, т.е. количество значений 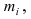приходящиеся на каждый разряд i (интервал 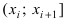). Вычисляют статистические относительные частоты попадания случайной величины X в интервал 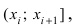т.е. величины 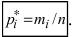Тогда статистическое распределение имеет вид, показанный таблицей.

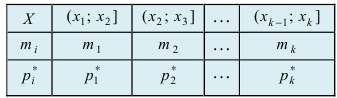
Число интервалов, на которые разбивается выборка, не должно быть слишком малым (в этом случае относительные частоты 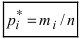обнаруживают незакономерные колебания) и слишком большим (в этом случае статистический ряд грубо описывает свойства распределения). Если число испытаний составляет от 200 до 300, то в предположении нормального распределения случайной величины X рекомендуется брать двенадцать интервалов. В большинстве практических случаев рекомендуют формулу Серджеса для определения шага h, определяющего длину интервала

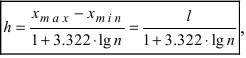где 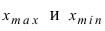- наибольшее и наименьшее значения случайной величины X в выборке, l - размах варьирования. Отметим, что концы интервалов необязательно должны совпадать с наблюденными значениями. За начало первого интервала выбирают значение 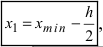все остальные значения концов интервалов вычисляют по формуле 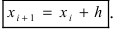Вычисление концов интервалов продолжается до тех пор, пока некоторое значение 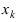не станет больше или равным наибольшему значению значения случайной величины X в выборке, т.е.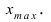

Пример:

Наблюдатель в течение 30 дней декабря измерял температуру воздуха (см. таблицу).

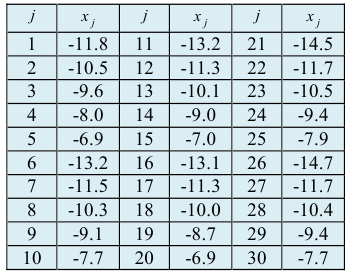
Найти статистическое распределение полученной выборки.

Решение:

Для приведенного примера проведем упорядочение полученной выборки

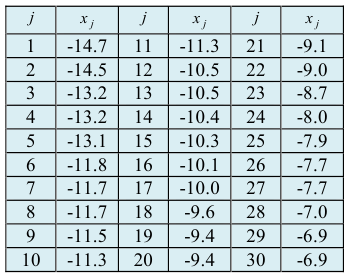
Вычислим размах варьирования 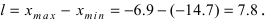В предположении, что исследуемая величина является случайной непрерывной величиной, вычислим по формуле Серджеса длину интервала:

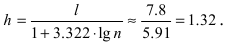
Замечание: При вычислении длины интервала всегда выбирают в значении шага на один разряд больше, чем число разрядов после запятой в данной таблице.

Вычислим концы интервалов:

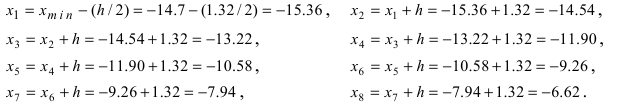
Следовательно, число интервалов равно 7. Таким образом,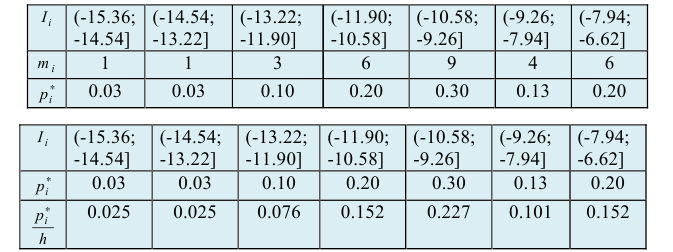

Полигон и гистограмма

Геометрическая иллюстрация статистических данных позволяет не только представить их в наглядной форме, но и проанализировать в простом и доступном виде. Если в прямоугольной системе координат (по оси абсцисс откладывают значения случайной величины X, а по оси ординат частоты (относительные частоты) попадания в интервал i) соединить точки, которые имеют координаты 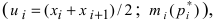то получим полигон частот (относительных частот (Рис. 14))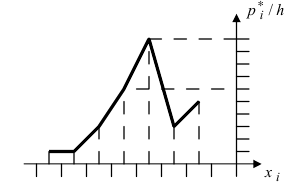

Рис. 14. Полигон относительных частот.

Если на каждом интервале построить прямоугольник высотой равной 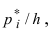то получим гистограмму относительных частот (Рис. 15):

Рис. 15. Гистограмма относительных частот.

Статистическая функция распределения

Определение: Статистической функцией распределения случайной величины X называется закон изменения относительной частоты события 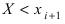для данного статистического интервала, т.е. 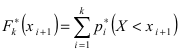или в развернутом виде:

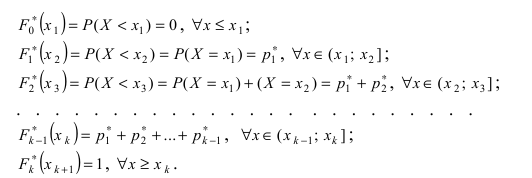
Для Примера статистическая функция распределения имеет вид (ступенчатый вид для случайной дискретной величины, и плавная кривая - для непрерывной величины) (Рис. 16):

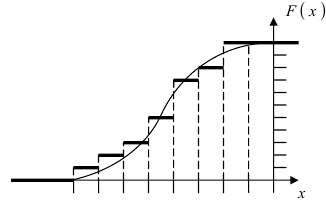
Рис. 16. Статистическая функция распределения для непрерывной (сплошная линия) или дискретной (ступеньки) случайной величины.

Замечание: Различие между функцией распределения F(x) и статистической функцией распределения состоит в том, что первая определяет вероят- ность события а вторая - относительную частоту появления того же события.

Оценки параметров распределения

Большинство случайных величин подчиняются нормальному закону распределения, поэтому предположим, что исследуемая случайная величина является нормальной случайной величиной. При решении второй задачи математической статистики (оценка параметров распределения) применяют точечные и интервальные оценки параметров распределения.

Точечные оценки

Любое значение искомого параметра, вычисленное на основе ограниченного числа опытных данных, всегда содержит элемент случайности. Рассмотрим точечные оценки искомых параметров.

Определение: Приближенное случайное значение параметра 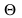называется его оценкой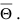

Определение: Оценка 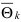называется состоятельной оценкой параметра 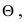если для любого положительного числа 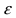последовательность оценок 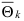сходится по вероятности к истинному значению параметра 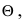т.е.

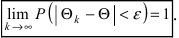
Определение: Оценка 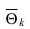называется несмещенной оценкой параметра 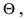если математическое ожидание оценки равно истинному параметру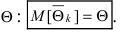

Замечание: Это требование гарантирует отсутствие систематических ошибок при оценке искомого параметра.

Определение: Оценка 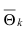называется эффективной оценкой параметра 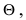если её дисперсия является наименьшей из всех дисперсий оценок искомого параметра.

Определение: Оценка 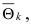удовлетворяющая требованиям состоятельности, несмещенности и эффективности, называется подходящей или хорошей оценкой параметра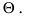

На практике не всегда удается одновременно удовлетворить всем требованием хорошей оценки. Поэтому укажем способ получения хорошей оценки для основных параметров распределения: математического ожидания и дисперсии. Пусть дискретная или случайная непрерывная величина X при проведении серии независимых испытаний принимает набор значений 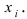В качестве оценки математического ожидания принимают среднее арифметическое (наиболее вероятное значение случайной величины X) полученных

данных, т.е.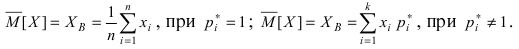

Определение: Величина 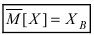в называется выборочной средней.

Замечание: В дальнейшем для простоты рассуждений будем рассматривать случай, когда все полученные экспериментальные данные 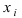различны, т.е. относительная частота значения 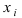равна единице.

На основании теоремы Чебышева эта оценка математического ожидания является состоятельной. Покажем, что эта оценка является несмещенной, так как 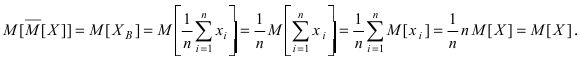Если случайная величина X распределена по нормальному закону, то приведенная оценка математического ожидания является эффективной. В качестве оценки дисперсии D[Х] используется статистическая дисперсия 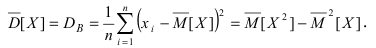Согласно теореме Чебышева эта оценка дисперсии является состоятельной, но смещенной, так как 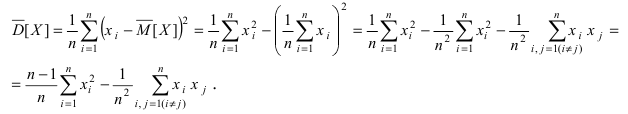Следовательно, математическое ожидание этой оценки равно: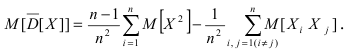

Так как оценка 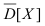не зависит от того, в какой точке выбрать начало координат, то выберем его в точке 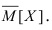Тогда 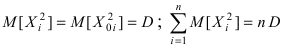и величина 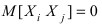в силу независимости экспериментов. Следовательно, 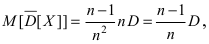т.е. оценка дисперсии является смещенной. Вводя исправленную оценку дисперсии 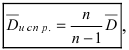получим несмещенную оценку дисперсии.

Замечание: Если относительная частота появления значения 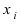отлична от единицы, то оценка дисперсии равна 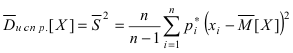или общая формула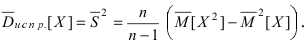

Метод максимального правдоподобия для нахождения оценок параметров распределения.

Если распределение случайной величины X содержит параметр 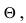который не выражается через математическое ожидание и дисперсию, то нахождения оценки такого параметра используют метод максимального правдоподобия.

Суть этого метода состоит в следующем:

• вводят функцию правдоподобия 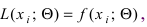где 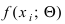- плотность
• вероятности;
• так как экстремумы функции 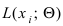совпадают с экстремумами 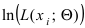, то для нахождения оценки параметра 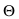решают уравнение правдоподобия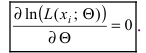

Замечание: Если испытания независимы в смысле теории вероятностей, то функция правдоподобия выбирается в виде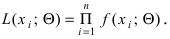

Замечание: Если распределение случайной величины X содержит k параметров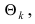 не выражаемых через математическое ожидание и дисперсию, то уравнения правдоподооия имеют вид: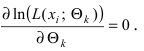

Пример:

Найти оценку параметра 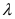распределения Пуассона по методу максимального правдоподобия.

Решение:

Так как ряд 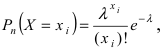где n - число проведенных испытаний, 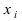-число появлений некоторого события А в опыте i. Функция правдоподобия имеет вид:

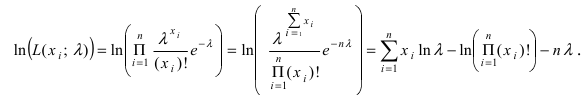Воспользуемся уравнением правдоподобия 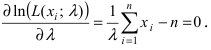Отсюда следует 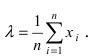Сравнив полученное выражение с выражением математического ожидания видим, что оценка 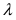совпадает с математическим ожиданием.

Интервальные оценки

При малом числе опытов точечная оценка параметра распределения дает довольно грубое приближение этого параметра. Поэтому при небольшом числе наблюдений используют интервальную оценку, которая определяет доверительный интервал для значений оцениваемого параметра. Если величина 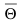является оценкой параметра 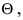то с точностью 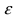и надежностью 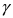должно выполняться равенство 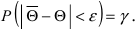Это равенство утверждает, что с доверительной вероятностью 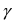случайный параметр 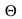попадает в интервал 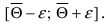Ранее в теории вероятностей был рассмотрен случай, когда случайная величина X попадала в заданный (неслучайный) интервал. Для исследуемой задачи необходимо знать закон распределения оценки 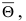который зависит от распределения случайной величины X, а, следовательно, и от самого оцениваемого параметра 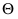и от числа проведенных испытаний n. Если 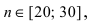то указанное затруднение обходится путем замены неизвестных параметров на их оценки. В качестве примера построим доверительный интервал для математического ожидания случайной величины X. Пусть произведено n независимых испытаний над случайной величиной X, математическое ожидание и дисперсия которой равны 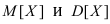, соответственно. Их точечные статистические оценки обозначим посредством 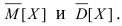Согласно теореме Ляпунова случайная оценка математического ожидания 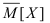распределена по нормальному закону с параметрами:

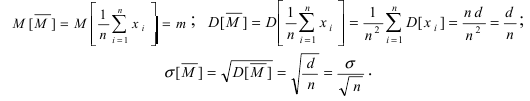Найдем такую величину 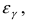для которой выполняется равенство:

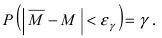
В силу того, что случайная оценка математического ожидания распределена по нормальному закону, то 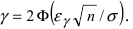Отсюда следует, что 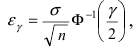где 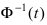- функция, обратная к функции Лапласа 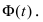Заменяя величину 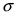по ее определению на величину 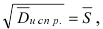получим следующее выражение для доверительного интервала: 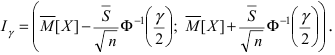Аналогично строится доверительный интервал для дисперсии.

Точные методы построения интервалов для нормальной случайной величины

Для точного построения доверительных интервалов надо знать закон распределения случайной величины X. Если X - нормальная случайная величина, то можно показать, что величины:

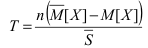- подчиняется распределению Стьюдента с (n-1) степенями свободы” (т.е. распределение характеризуется (n-1) связью); 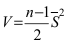- распределена по закону “хи-квадрат 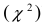” (законы Стьюдента и “хи-квадрат 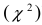” приведены в Лекции № 4). Применим распределение Стьюдента для построения точного доверительного интервала для математического ожидания нормальной случайной величины X.

Пусть выполняется равенство 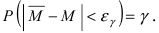Тогда для случайной величины 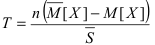будет выполняться равенство 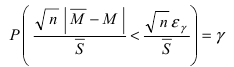или в принятых обозначениях 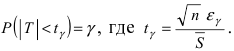Используя таблицы для распределения Стьюдента по заданной величине 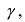находят значение 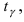по которому вычисляют точность измерений 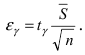Записывают доверительный интервал для математического ожидания:

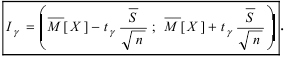Аналогичные рассуждения для дисперсии приводят к следующему выражению для доверительного интервала: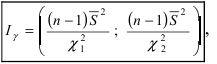

где величины 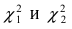определяют по известному числу "степеней свободы" и заданной надежности измерений 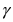по таблицам для распределения “хи-квадрат 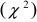” из соотношений

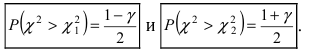
Замечание: Под “степенями свободы" понимают число ограничений, накладываемых на случайную величину X. В качестве таких ограничений могут быть выбраны следующие равенства: 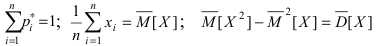- и другие соотношения.

Замечание: Число “степеней свободы'" можно определить по формуле 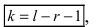где l- количество интервалов, на которые разбивается выборочная совокупность, r - число параметров входящих в закон распределения (для нормального закона распределения r = 2, так как в выражение для плотности вероятности входят 2 параметра: m - математическое ожидание и 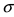- средне-квадратичное отклонение).

Метод последовательного анализа. Статистическая проверка гипотез

Пусть в результате проведения серии из n независимых испытаний для случайной величины X получен статистический ряд её значений 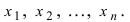После обработки опытных данных находят статистическую функцию распределения, вычисляют оценки параметров и выдвигают гипотезу H относительно закона распределения случайной величины X. Для проверки принятой гипотезы H (третья задача математической статистики) существует несколько математических методов. Одним из таких методов является метод последовательного анализа, сущность которого состоит в следующем:

• выбирают критерий проверки (например, саму случайную величину X, значения которой зависят от номера проведенного опыта);
• назначают точность эксперимента и надежность получаемых результатов;
• проводят испытания и определяют значение критерия проверки;
• если критерий проверки соответствует принятой гипотезе H, то она принимается, в противном случае - отвергается.

Если по методу последовательного анализа построить зависимость, например, случайной величины X от номера проводимого опыта, то получим 3 области, размеры которых определяются точностью эксперимента и уровнем надежности получаемых результатов в зависимости от принятой гипотезы Н о законе распределения случайной величины X (Рис. 17):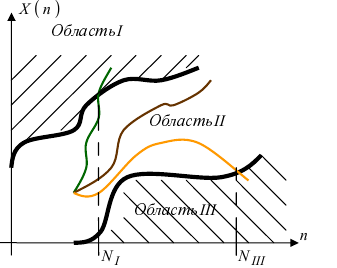

Рис. 17. Опытные области принятия или отклонения выдвинутых гипотез:

• Область I - область отклонения гипотезы Н.
• Область II - область проведения дальнейших испытаний (для подтверждения или отклонения гипотезы Н).
• Область III - область принятия гипотезы Н.

Если график зависимости 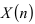входит в область I при числе опытов 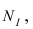, то гипотеза 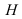заменяется новой гипотезой 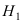(траектория (1)), и опыты повторяются. Если график зависимости 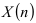находится в области II, то испытания продолжаются до тех пор, пока гипотеза 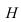будет либо отброшена, либо принята (траектория (2)). Если график зависимости 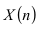входит в область III при числе опытов 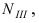то гипотеза 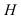принимается, и опыты прекращаются (траектория (3)). Для реализации метода последовательного анализа разработано несколько математических способов, из которых рассмотрим способ Пирсона (критерий 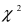) и способ академика А.Н. Колмогорова.

Способ Пирсона

Способ Пирсона (критерий ).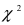

В способе Пирсона в качестве критерия проверки используется величина

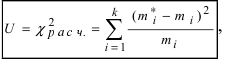где k - число интервалов, на которые разбивается вся выборка, n - число проведенных испытаний, 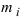- теоретическая частота попадания случайной величины X в интервал 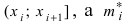- относительная частота попадания этой случайной величины в тот же интервал.

При увеличении числа опытов n случайная величина 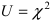практически не зависит от числа испытаний и её закон распределения приближается к закону распределения “хи-квадрат 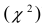”. Теоретические частоты 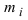вычисляются в соответствии с принятой гипотезой о законе распределения случайной величины X и оценкам её параметров распределения.

Вычисляя число “степеней свободы”, задавая уровень значимости (обычно принимают 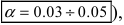по таблицам для распределения “хи-квадрат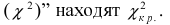

Если 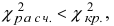то гипотеза принимается, в противном случае - отвергается.

Достоинством способа Пирсона является то, что он применим тогда, когда известен вид гипотетического распределения, но неизвестны его параметры.

К недостаткам этого способа относятся:

• - его применимость при числе опытов ;
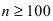• - количество интервалов 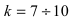и частота попадания в интервал ;
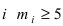• - результаты проверки зависят от способа разбиения выборки на интервалы.

Способ А.Н. Колмогорова

В этом способе в качестве критерия проверки выбирается случайная величина 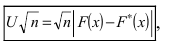которая представляет собой наибольшее значение разности между значениями теоретической 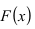и статистической 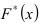функциями распределения.

Академик А.Н. Колмогоров доказал, что независимо от вида закона распределения случайной величины X при 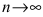существует предел вероятности того, что величина 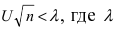- некоторое число. При достаточно большом числе опытов 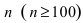выполняется приближенное равенство

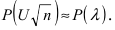
Отсюда следует схема применения способа А.Н. Колмогорова:

• вычисляют модуль наибольшей разности между теоретической и статистической функциями распределения и критерий проверки ;
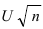• назначают уровень значимости 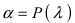(принимают );
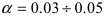• по соответствующим таблицам находят критическое значение величины 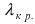из равенства ;
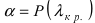• если расчетное значение критерия проверки 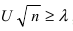, то гипотеза Н отбрасывается, в противном случае - принимается.

Достоинство способа А.Н. Колмогорова состоит в том, что он не требует сложных расчетов.

К недостаткам этого способа относятся:

• для применения этого способа надо знать не только вид закона распределения, но и его параметры;
• критерий проверки учитывает только модуль наибольшей разности между теоретической и статистической функциями распределения, но не закон изменения этого отклонения по всему объему выборки.