
Статика в физике - основные понятия, формулы и определения с примерами
Содержание:
Статика в физике:
До сих пор мы изучали движение тел. А нужно ли изучать состояние покоя тел? Безусловно, да! Ведь обеспечить состояние покоя и устойчивость домов, мостов, плотин, телевизионных вышек и т. д. — важнейшая практическая задача! Ее решением занимается статика.
Состояние тела, при котором оно остается неподвижным относительно данной инерциальной системы отсчета, называют состоянием механического равновесия.
Рассмотрим, при каких условиях тела находятся в состоянии равновесия.
Первое условие следует из второго закона Ньютона: для равновесия тела необходимо, чтобы векторная сумма всех сил, приложенных к нему, была равна нулю:
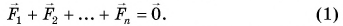
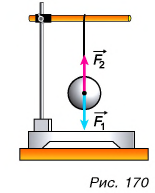
Например, для равновесия шарика (рис. 170) векторная сумма силы тяжести 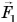
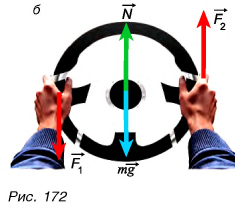
Но достаточно ли выполнения условия (1) для равновесия тела? Например, для тела, имеющего ось вращения: колеса автомобиля (рис. 171, а), колеса обозрения (рис. 171, б)у ворота (рис. 171, в), рулевого колеса (рис. 172) и т. д.?



Па рисунке 172, а на рулевое колесо действуют сила тяжести mg и сила реакции оси N. Их сумма 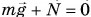 , и колесо находится в состоянии покоя. Останется ли рулевое колесо в покое, если к нему приложить еще две силы
, и колесо находится в состоянии покоя. Останется ли рулевое колесо в покое, если к нему приложить еще две силы 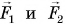 (рис. 172, б), модули которых равны, направления противоположны, а точки приложения не совпадают (такие силы в механике называют парой сил)?
(рис. 172, б), модули которых равны, направления противоположны, а точки приложения не совпадают (такие силы в механике называют парой сил)?
Несмотря на то что условие (1) по-прежнему выполняется: 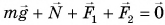 , руль не останется в покое. Из-за действия сил
, руль не останется в покое. Из-за действия сил 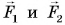 он будет поворачиваться вокруг своей оси. Значит, выполнения условия (1) для равновесия тел недостаточно. Какое еще условие должно выполняться, чтобы не возникало вращения тела?
он будет поворачиваться вокруг своей оси. Значит, выполнения условия (1) для равновесия тел недостаточно. Какое еще условие должно выполняться, чтобы не возникало вращения тела?
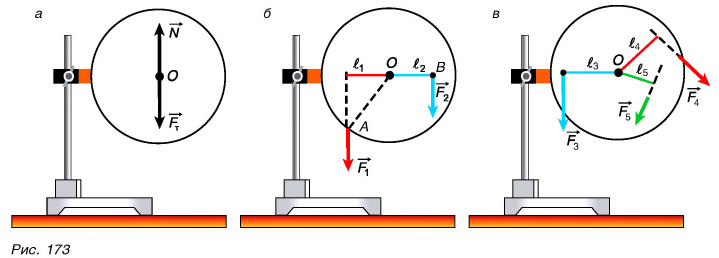
Для ответа на вопрос проведем опыты с диском (рис. 173, а), имеющим горизонтальную ось вращения, проходящую через его центр — точку О. С помощью штырей, вставленных в отверстия, и нитей будем прикладывать к диску силы, имеющие различные направления, точки приложения и модули (рис. 173, б и в).
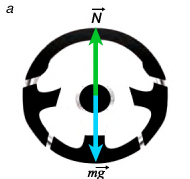
Сила тяжести диска FT и сила реакции N оси приложены к диску в его центре (рис. 173, а). Они не вызывают вращения диска, и на рисунках 173, б, в мы их показывать не будем. Поворот диска могут вызвать только те силы, которые действуют вдоль линии, не проходящей через ось вращения (рис. 173, б, в).
Расстояние от оси вращения до линии действия силы называют плечом силы.
На рисунке 173, б расстояние 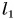 — это плечо силы
— это плечо силы 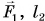 — силы
— силы 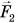 .
.
На рисунке 173, б сила 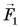 , стремится повернуть диск против хода часовой стрелки, а сила
, стремится повернуть диск против хода часовой стрелки, а сила 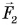 — по ходу часовой стрелки. Куда в итоге повернется диск?
— по ходу часовой стрелки. Куда в итоге повернется диск?
Опыты показывают: если 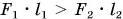 то диск повернется против хода часовой стрелки, если
то диск повернется против хода часовой стрелки, если 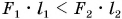 — по ходу часовой стрелки. А при выполнении условия
— по ходу часовой стрелки. А при выполнении условия

диск будет находиться в состоянии равновесия.
Произведение модуля силы на ее плечо называют моментом силы (вращающим моментом).
Момент силы может быть положительным или отрицательным. Все зависит от того, в какую сторону сила стремится повернуть тело вокруг данной оси. Если против хода часовой стрелки, то 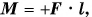 если по ходу, то
если по ходу, то 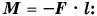

Единица момента силы в СИ — ньютон-метр (Н * м). Один ньютон-метр равен вращающему моменту, создаваемому силой 1 ньютон, имеющей плечо 1 метр.
Условие равновесия (2), выраженное через моменты сил с учетом их знаков, примет вид 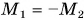 , или
, или

А если к телу приложено более двух сил (рис. 173, в)? Тогда, как показывает опыт, для равновесия необходимо равенство нулю алгебраической суммы моментов всех сил, действующих на тело:
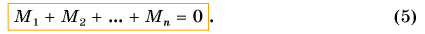
Это и есть второе условие равновесия. Момент силы очень важен для практики! Например, если при закручивании болта или гайки мы приложим слишком большой вращающий момент, то резьба будет сорвана. Для ответственных работ используют гаечные Рис. 174 ключи с датчиком вращающего момента (рис. 174).

Главные выводы
- Плечо силы — это расстояние от оси вращения до линии действия силы.
- Момент силы равен произведению модуля силы и ее плеча, взятому со знаком «плюс» или «минус».
- Тело, имеющее неподвижную ось вращения, будет находиться в равновесии, если алгебраическая сумма моментов сил, приложенных к нему, равна нулю.
Простые механизмы
Посетите цех современного завода и понаблюдайте, как работают машины. Они, как разумные существа, прессуют, гнут, режут металлические листы, считают, сортируют, взвешивают, перемещают и упаковывают изделия. Эти огромные и маленькие машины-автоматы, машины-роботы действуют быстрее и точнее человека.
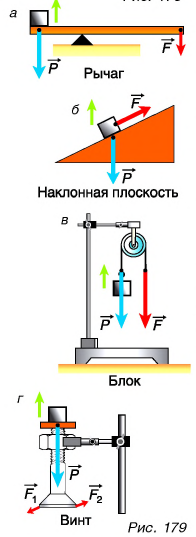
Однако даже у таких сложных устройств, как роботы (рис. 178), механическая часть является комбинацией простых механизмов: рычагов, наклонных плоскостей, блоков, винтов (рис. 179).
Элементы простых механизмов мы обнаружим у ворота (см. рис. 171, в, с. 118), гаечного ключа (см. рис. 174, с. 120), топора (рис. 180) и т. д.
Зачем нужны простые механизмы? На рисунке 179, а — в показано, как, приложив силу F или силы 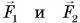 (рис. 179, г) к механизму, можно поднять груз весом Р. Данные силы, однако, не приложены непосредственно к грузу (кроме случая б) и не направлены вверх. Значит, простой механизм дает возможность изменить точку приложения силы и ее направление. Кроме того, он позволяет поднять груз силой, гораздо меньшей, чем вес этого груза (случаи а, б, г), т. е. дает выигрыш в силе.
(рис. 179, г) к механизму, можно поднять груз весом Р. Данные силы, однако, не приложены непосредственно к грузу (кроме случая б) и не направлены вверх. Значит, простой механизм дает возможность изменить точку приложения силы и ее направление. Кроме того, он позволяет поднять груз силой, гораздо меньшей, чем вес этого груза (случаи а, б, г), т. е. дает выигрыш в силе.
Что такое выигрыш в силе? От чего он зависит? Рассмотрим это на примере рычага (рис. 181).


Рычагом может служить твердое тело, способное вращаться вокруг заданной оси (или точки опоры).
Различают рычаги первого и второго рода. У рычага первого рода (рис. 181, а) вес поднимаемого груза Р и приложенная сила F находятся по разные стороны от точки опоры О, а у рычага второго рода — но одну сторону от нее (рис. 181, б).
В обоих случаях вес Р груза больше, чем приложенная сила F. Значит, рычаг дает выигрыш в силе.
Найдем выигрыш в силе для рычага первого рода (рис. 181, а). Обозначим плечи сил 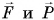 относительно точки опоры О через
относительно точки опоры О через 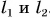 . Плечо силы реакции опоры N равно нулю. Как мы знаем, при равновесии моменты сил компенсируют друг друга:
. Плечо силы реакции опоры N равно нулю. Как мы знаем, при равновесии моменты сил компенсируют друг друга: 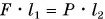 . В результате
. В результате
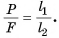
Итак, выигрыш в силе для рычага равен отношению плеча прикладываемой силы к плечу веса поднимаемого груза. Докажите самостоятельно, что формула 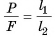 справедлива и для рычага второго рода.
справедлива и для рычага второго рода.
Рассмотрим блоки (рис. 182). Их широко используют на стройках, в портах, на складах и т. д.
Блок представляет собой колесо с желобом, через который проходит трос (канат, веревка, нить и т. д.). Если ось блока закреплена (рис. 183, а), то блок называют неподвижным, если нет, то — подвижным (рис. 185, а).
Дает ли блок выигрыш в силе? Проведем опыт с неподвижным блоком (рис. 183, а). К одному концу нити, перекинутой через блок, прикрепим груз, а к другому — динамометр. При покое или равномерном подъеме груза показания динамометра F практически равны весу груза Р. Почему неподвижный блок не дает выигрыша в силе?
На рисунке 183, б изображены силы, действующие на блок: сила тяжести блока 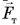 , сила реакции оси
, сила реакции оси 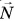 и силы упругости нитей
и силы упругости нитей 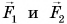 . Будем рассматривать блок как рычаг первого рода. Относительно оси блока О плечи сил
. Будем рассматривать блок как рычаг первого рода. Относительно оси блока О плечи сил 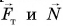 равны нулю, а плечи сил
равны нулю, а плечи сил 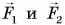 — радиусу блока:
— радиусу блока: 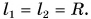
По правилу моментов: 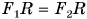 , откуда
, откуда 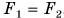 . Учитывая, что
. Учитывая, что 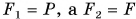 , получим Р = F.
, получим Р = F.
Неподвижный блок не дает выигрыша в силе, а лишь изменяет ее направление.
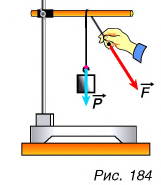
Зачем же применять неподвижный блок, если выигрыша в силе нет? Ведь для изменения направления силы можно взять любую перекладину (рис. 184). Можно, но невыгодно, так как потери на трение будут во много раз больше, чем при использовании блока.
Проведем теперь опыт с подвижным блоком (рис. 185, а), ось которого О перемещается вместе с грузом. Один конец перекинутой через блок нити закрепим, а за другой будем поднимать груз. При равномерном подъеме груза весом Р = 4 Н (как и в состоянии покоя) показания динамометра F 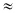 2 Н, т. е. почти в два раза меньше веса груза (рис. 185, а).
2 Н, т. е. почти в два раза меньше веса груза (рис. 185, а).
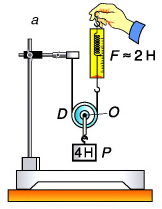
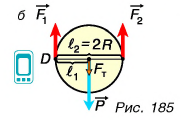
Этот результат вполне понятен. Ведь блок с грузом удерживают две нити. Сила натяжения каждой из нитей равна половине веса груза. Чтобы доказать это, будем рассматривать блок как рычаг второго рода с осыо в точке D (рис. 185, б). Относительно этой оси у силы натяжения нити F, плечо равно нулю, а у силы натяжения F2 оно равно 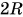 , а плечи силы тяжести блока
, а плечи силы тяжести блока 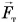 и веса груза
и веса груза 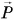 равны R. Тогда, по правилу моментов,
равны R. Тогда, по правилу моментов, 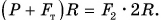 Отсюда, пренебрегая силой
Отсюда, пренебрегая силой 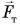 находим:
находим: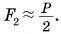 Так как F2 = F, то
Так как F2 = F, то 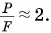
Подвижный блок дает выигрыш в силе приблизительно в 2 раза. Отметим, что при расчетах мы не учитывали силу трения на оси блока.
Для любознательных:
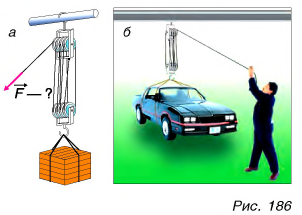
Гораздо больший выигрыш в силе дает полиспаст — устройство, состоящее из нескольких пар подвижных и неподвижных блоков. При трех парах блоков (рис. 186, а) и отсутствии трения полиспаст дат бы выигрыш в силе, равный 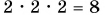 (на самом деле выигрыш будет несколько меньше). Полиспасты широко используют для подъема тяжестей. Оцените количество блоков, при котором полиспаст даст возможность поднять автомобиль усилиями всего одного человека (рис. 186, б).
(на самом деле выигрыш будет несколько меньше). Полиспасты широко используют для подъема тяжестей. Оцените количество блоков, при котором полиспаст даст возможность поднять автомобиль усилиями всего одного человека (рис. 186, б).
Главные выводы:
- Простые механизмы дают возможность изменить точку приложения силы, ее модуль и направление.
- Рычаг дает выигрыш в силе во столько раз, во сколько раз плечо прилагаемой силы больше плеча веса поднимаемого груза.
- Неподвижный блок не дает выигрыша в силе; а лишь изменяет ее направление.
- Подвижный блок дает выигрыш в силе в 2 раза (если пренебречь весом блока и трением).
Пример №1
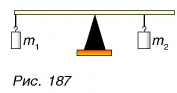
На одном конце линейки длиной l = 1,0 м подвешен груз массой 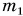 = 450 г (рис. 187). Посередине линейки снизу находится опора, относительно которой линейка может свободно поворачиваться в вертикальной плоскости. На каком расстоянии от точки опоры линейки подвешен груз массой
= 450 г (рис. 187). Посередине линейки снизу находится опора, относительно которой линейка может свободно поворачиваться в вертикальной плоскости. На каком расстоянии от точки опоры линейки подвешен груз массой 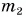 = 750 г, если линейка, располагаясь горизонтально, находится в равновесии?
= 750 г, если линейка, располагаясь горизонтально, находится в равновесии?
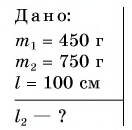
Решение
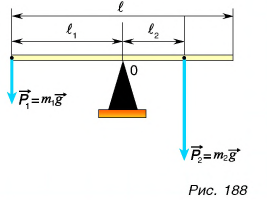
Из сил, действующих на линейку, на рисунке 188 покажем только те, моменты которых относительно точки О не равны пулю.
По условию равновесия 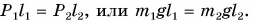 Откуда
Откуда
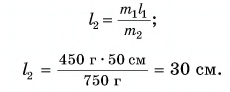
Ответ: 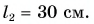
Пример №2
Какую минимальную силу нужно приложить к концу веревки для подъема мешка цемента массой 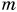 = 50 кг на второй этаж строящегося дома с помощью подвижного блока?
= 50 кг на второй этаж строящегося дома с помощью подвижного блока?
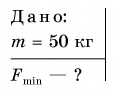
Решение
Так как блок подвижный, то:
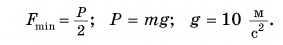
Тогда:
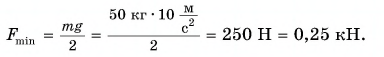
Ответ: 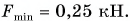
Наклонная плоскость и золотое правило механики
На примере рычагов и блоков мы узнали, что с помощью простых механизмов можно получить выигрыш в силе. А можно ли получить выигрыш в работе?
Прежде чем ответить на этот вопрос, изучим еще один простой механизм — наклонную плоскость. Она служит основой таких конструкций, как пандусы, эскалаторы, конвейеры и т. д. (рис. 192).
Дает ли применение наклонной плоскости выигрыш в силе? Рассмотрим пример. Грузчик перемещает тяжелый контейнер по наклонной плоскости (рис. 192, г). Cила, которую он при этом прикладывает, гораздо меньше, чем вес контейнера.

Как рассчитать выигрыш в силе, который дает наклонная плоскость?
Проведем простой опыт. Поместим брусок массой m на наклонную плоскость длиной l = АВ и высотой h = ВС (рис. 193). Приложив к нему с помощью динамометра силу 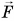 параллельную наклонной плоскости, будем равномерно перемещать брусок вдоль нее. Показания динамометра F будут меньше, чем значение силы тяжести бруса
параллельную наклонной плоскости, будем равномерно перемещать брусок вдоль нее. Показания динамометра F будут меньше, чем значение силы тяжести бруса 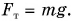 Отношение
Отношение 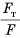 определяет выигрыш в силе. От чего он зависит?
определяет выигрыш в силе. От чего он зависит?
Рассмотрим все силы, действующие на брусок. Кроме силы 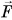 и силы тяжести
и силы тяжести 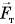 на брусок действует сила реакции наклонной плоскости
на брусок действует сила реакции наклонной плоскости 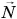 . При отсутствии трения она перпендикулярна наклонной плоскости. Силу
. При отсутствии трения она перпендикулярна наклонной плоскости. Силу 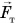 разложим на две составляющие:
разложим на две составляющие: 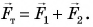
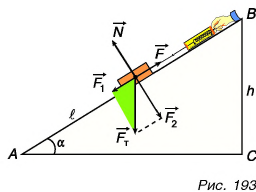
Из подобия треугольника сил (выделенного цветом) и 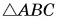 следует:
следует:

Так как при равномерном подъеме 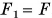 то:
то:

Выигрыш в силе, получаемый с помощью наклонной плоскости, равен отношению ее длины к ее высоте (при отсутствии трения). Чем меньше угол наклона а плоскости к горизонту, тем больше отношение 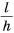 , а значит, тем больше выигрыш в силе. Это подтверждается нашими повседневными наблюдениями. Тянуть санки, катить багажную тележку вверх но пологому склону гораздо легче, чем но крутому.
, а значит, тем больше выигрыш в силе. Это подтверждается нашими повседневными наблюдениями. Тянуть санки, катить багажную тележку вверх но пологому склону гораздо легче, чем но крутому.
При выводе формулы (2) мы не учитывали трения. Но на самом деле трение есть. Из-за него при подъеме бруска приходится прилагать большую силу, и выигрыш в силе будет меньшим.
На практике для уменьшения трения проводят смазку деталей, заменяют скольжение качением, применяют «воздушную подушку» (рис. 194).

Для любознательных
Идея наклонной плоскости заложена и в таких механизмах, как клин и винт. Разновидностью клина является топор, дающий большой выигрыш в силе. Винтовые домкраты (рис. 195, а) применяют для подъема автомобилей и других массивных объектов.
Винты, болты, шурупы (рис. 195, б) используют для соединения деталей. При этом трение приносит как вред, так и пользу. Оно затрудняет завинчивание, но предотвращает самопроизвольное ослабление резьбовых соединений.

Мы выяснили, что большинство простых механизмов дают выигрыш в силе. А дают ли они выигрыш в работе?
С физической величиной, называемой «работа», и с ее единицей в СИ джоулем вы познакомились в 7-м классе.
Для любознательных
Среди всех физических величин работа занимает особое место. Tie совершив работы, нельзя привести в движение поезд, автомобиль, корабль, самолет, ракету и т. д. Нельзя перевезти груз, подняться на нужный этаж (ни пешком, ни на лифте). Невозможно построить дом и любое другое сооружение.
Производственная деятельность невозможна без совершения работы.
Значимость работы еще шире. Непрерывно совершать работу необходимо для поддержания жизни. Наше сердце при каждом ударе совершает работу, примерно равную одному джоулю.
Рассмотрим работу различных простых механизмов. Силу трения пока учитывать не будем.
Наклонная плоскость. Для нее полезная работа — это работа по подъему груза на высоту h: 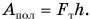 Совершенная работа прилагаемой силы
Совершенная работа прилагаемой силы 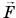 по перемещению груза по наклонной плоскости на пути l равна:
по перемещению груза по наклонной плоскости на пути l равна: 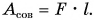 Из равенства (2)
Из равенства (2) 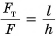 получим:
получим: 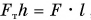 , т. е.
, т. е.
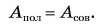
Наклонная плоскость не дает выигрыша в работе.
Неподвижный блок. Для него равны и модули сил, и пройденные пути (см. рис. 183, с. 123), а значит, и соответствующие работы. Неподвижный блок выигрыша в работе не дает.
Подвижный блок. Он дает выигрыш в силе, близкий к двум, но и двукратный проигрыш в пути (см. рис. 185, с. 124). Подвижный блок также не дает выигрыша в работе.
Рычаг. Выигрыша в работе не дает и рычаг (как первого, так и второго рода). Докажите это самостоятельно.
Все опыты подтверждают: если с помощью простого механизма выигрывают в силе, то по меньшей мере во столько же раз проигрывают в пути. Учитывая, что даже самый сложный механизм сводится к сочетанию простых механизмов, можно сделать вывод: ни один механизм не дает выигрыша в работе. Это утверждение получило название «золотое правило механики».
Итак, выиграть в работе нельзя. А вот проиграть — можно. Причина этому — сила трения. Кроме того, существуют и другие потери, например работа по подъему самого механизма в процессе его использования. Из-за этого совершенная работа 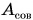 всегда больше, чем полезная работа
всегда больше, чем полезная работа 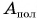 :
:
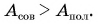
Отношение 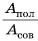 называется коэффициентом полезного действия (КПД). КПД, выраженный в процентах, равен:
называется коэффициентом полезного действия (КПД). КПД, выраженный в процентах, равен:
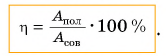
Так как совершенная работа всегда больше полезной, КПД механизма всегда меньше единицы (т. е. меньше 100 %). Чтобы увеличить КПД, необходимо уменьшить «бесполезную» работу. Прежде всего — работу по преодолению сил трения.
Машина, которая имела бы 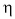 = 100 % или более, называется вечным двигателем. Весь опыт развития науки и техники говорит о том, что вечный двигатель неосуществим. Заметим, однако, что попытки его изобрести не прекращаются до сих пор.
= 100 % или более, называется вечным двигателем. Весь опыт развития науки и техники говорит о том, что вечный двигатель неосуществим. Заметим, однако, что попытки его изобрести не прекращаются до сих пор.
Для любознательных:
Идея создания вечного двигателя возникла в далеком прошлом. На его создание были направлены усилия изобретателей на протяжении нескольких веков.
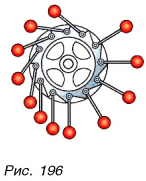
На рисунке 196 изображен один из проектов вечного двигателя. Разберитесь самостоятельно или с помощью учителя: почему автор устройства считал, что оно будет самопроизвольно вечно вращаться? Чего не учел автор?
Главные выводы:
- Наклонная плоскость дает выигрыш в силе во столько раз, во сколько раз ее длина больше высоты.
- Ни один механизм не дает выигрыша в работе: во сколько раз выигрывают в силе, во столько раз проигрывают в пути.
- Из-за силы трения и других потерь коэффициент полезного действия любого механизма меньше 100 %.
Пример №3
С помощью подвижного блока ведро песка массой m = 20 кг поднимают на высоту h = 4,0 м, прилагая к канату силу F = 110 Н. Определите совершенную при этом подъеме работу и КПД блока. Модуль ускорения свободного падения 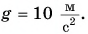
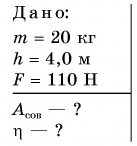
Решение
При использовании подвижного блока происходит проигрыш в пути в 2 раза, т. е. s = 2h. Совершенная работа:
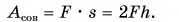
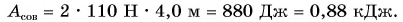
Полезная работа по подъему ведра с песком:
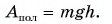
КПД блока:

Ответ: 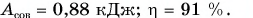
Центр тяжести и виды равновесия
Читаем сводку очередного происшествия: «Из-за смещения центра тяжести корабль потерял устойчивость». А что такое «центр тяжести»? Что такое «устойчивость»?
Центром тяжести тела называется точка приложения силы тяжести, действующей на него.
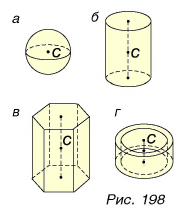
У однородных тел правильной формы центр тяжести находится в геометрическом центре тела (рис. 198, а, б, в, г). При этом центр тяжести может не совпадать ни с одной из точек этого тела (рис. 198, г).
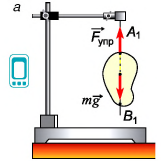
Л как найти центр тяжести тела произвольной формы? Это можно сделать с помощью простого опыта. Подвесим пластину на нити, прикрепленной к ней в некоторой точке 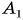 (рис. 199, а). Центр тяжести пластины будет находиться на одной линии с нитью — на вертикальной прямой
(рис. 199, а). Центр тяжести пластины будет находиться на одной линии с нитью — на вертикальной прямой 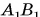 . Отметим на пластине эту прямую.
. Отметим на пластине эту прямую.
Изменим точку подвеса (рис. 199, б) и отметим вертикаль 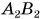 . Точка С, лежащая на пересечении прямых
. Точка С, лежащая на пересечении прямых 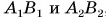 , — центр тяжести пластины.
, — центр тяжести пластины.
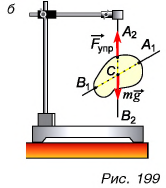
Центр тяжести тела можно определить путем расчетов.
Например, для тела, состоящего из двух грузов, соединенных легким стержнем (рис. 200), с помощью правила моментов легко найти отношение расстояний от центра тяжести С до грузов: 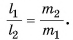
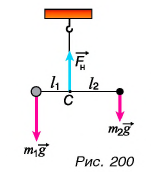
Следовательно, центр тяжести расположен ближе к более массивному грузу.
Положение центра тяжести очень важно для устойчивости высотных сооружений, подъемных кранов, автомобилей, кораблей и т. д. Смещение центра тяжести судна из-за неправильной загрузки может привести к его опрокидыванию.
А что такое устойчивость? От чего она зависит?
Проведем опыт. Поместим шарик 1 в лунку (рис. 201, а), шарик 2 — на вершину горки (рис. 201, б), а шарик 3 — на горизонтальную поверхность (рис. 201, в). Каждый из шариков находится в состоянии равновесия (в покое).
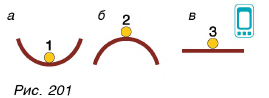
Отклоним шарики от положений равновесия и отпустим. Шарик 1 вернется в исходную точку (рис. 202, а), шарик 2 отклонится от исходного положения еще больше (рис. 202, б). Шарик 3 останется в состоянии равновесия (рис. 202, в).
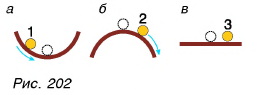
Каждый случай соответствует одному из трех видов равновесия: а — устойчивому, б — неустойчивому, в — безразличному.
Равновесие называется устойчивым, если при малом отклонении от него тело возвращается в исходное положение, неустойчивым — если отдаляется от него еще больше, безразличным — если остается в равновесии.
Почему в нашем опыте шарики вели себя по-разному? Все зависело от результирующей силы 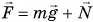 (рис. 203), действующей на шарик при его отклонении от положения равновесия. В случае а сила F была направлена к положению равновесия, в случае б — от него. В случае в сила F была равна нулю.
(рис. 203), действующей на шарик при его отклонении от положения равновесия. В случае а сила F была направлена к положению равновесия, в случае б — от него. В случае в сила F была равна нулю.

А как при этом изменялась потенциальная энергия тела?
Из рисунка 203 понятно, что потенциальная энергия тела при его отклонении от положения устойчивого равновесия увеличивалась, от неустойчивого — уменьшалась, от безразличного — не изменялась. Значит, положению устойчивого равновесия соответствует минимум потенциальной энергии.
Проведем еще один опыт. Расположим на горизонтальной доске три одинаковых бруска Ау Б и В (рис. 204).
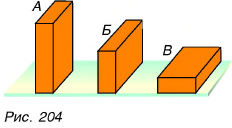
Какой из брусков находится в состоянии равновесия? Все три.
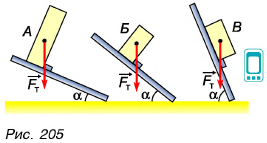
Но одинакова ли степень устойчивости состояний этих брусков? Продолжим опыт (рис. 205). Будем постепенно наклонять доску, оставляя на ней по одному бруску (чтобы брусок при этом не соскальзывал, приделаем к доске небольшую ступеньку). Первым опрокинется брусок А, вторым — Б? третьим — В.
Значит, степень устойчивости равновесия у брусков разная. Почему? Потому, что опрокидывание тела происходит тогда, когда линия действия силы тяжести выходит за пределы опорной площадки. Видно, что угол опрокидывания а тем больше, чем больше размеры этой площадки и чем ниже расположен центр тяжести тела.
Сделаем практически важный вывод: чем ниже центр тяжести тела и чем больше опорная площадка, тем состояние тела более устойчиво.
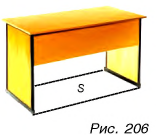
Обратите внимание: опорная площадка — ото плоскость, ограниченная прямыми, проходящими через крайние точки контакта тела с опорой. Площадь S опорной площадки может во много раз превосходить площадь непосредственного контакта тела с поверхностью опоры (рис. 206).
Для любознательных:
Достаточная опорная площадка и правильное положение центра тялсести предусматривается в конструкции всех высотных сооружений. Так, устойчивость 540-метровой Останкинской телебашни (рис. 207) обеспечивается прежде всего тем, что ее центр тяжести находится практически на уровне земли. Это обеспечено заглублением в землю железобетонного фундамента массой около 200 000 тонн.

Главные выводы:
- Точка приложения силы тяжести тела называется центром тяжести.
- Существует три вида равновесия: устойчивое, неустойчивое и безразличное.
- Чем ниже расположен центр тяжести тела и чем больше опорная площадь, тем более устойчиво состояние тела.
Пример №4
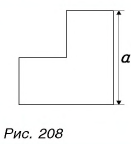
Из однородной квадратной пластинки со стороной a = 10 см вырезана 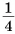 часть (рис. 208).
часть (рис. 208).
Определите положение центра тяжести пластинки с вырезом.
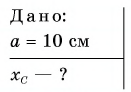
Решение
Для определения положения центра (точки С) вернем на свое место вырезанную часть (рис. 209). Сила тяжести всей пластинки будет равна сумме сил тяжести вырезанной части 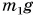 и оставшейся части
и оставшейся части 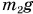 . Относительно точки О алгебраическая сумма моментов этих сил равна нулю:
. Относительно точки О алгебраическая сумма моментов этих сил равна нулю:
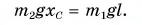
Отсюда
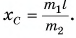
Так как 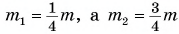 , то
, то 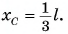
Поскольку плечо 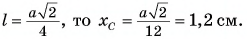
Ответ: 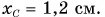
Действие жидкости и газа на погруженные в них тела. Выталкивающая сила. Закон Архимеда
До сих пор мы рассматривали равновесие тел, не учитывая влияние среды (жидкости, газа), в которой они находятся. А как влияет среда на равновесие тел?
Погруженный в воду мяч всплывает, воздушные шары (рис. 210, а) поднимаются вверх, шары-зонды (рис. 210, б) улетают на огромную высоту. Какая сила устремляет их вверх?

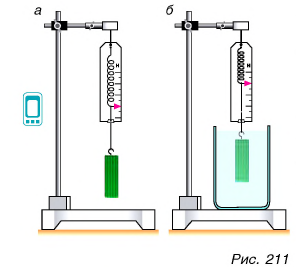
Проведем опыт. К динамометру подвесим пластилиновый брусок (рис. 211, а). Опустим брусок в воду (рис. 211,6). Показания динамометра уменьшатся. Значит, на погруженное тело со стороны жидкости действует направленная вверх выталкивающая сила. Ее значение равно разности показаний динамометра до и после погружения тела.
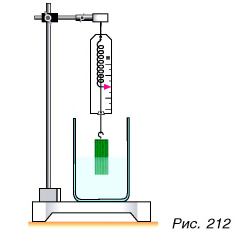
От чего зависит выталкивающая сила? Сравним значения вытал кивающей силы при полном (рис. 211, б) и частичном (рис. 212) погружении бруска. Мы убеждаемся, что выталкивающая сила тем больше, чем больше объем погруженной части тела.
А зависит ли выталкивающая сила от плотности жидкости? Продолжим опыты. Погрузим пластилиновый брусок в раствор поваренной соли в воде. Повышая концентрацию соли, будем увеличивать плотность раствора. Опыт показывает: при увеличении плотности жидкости выталкивающая сила возрастает.
Итак, выталкивающая сила тем больше, чем больше объем погруженной в нее части тела и чем больше плотность жидкости.
Выталкивающая сила действует и на тела, находящиеся в газе (рис. 213, а, б).
А как на выталкивающую силу влияет плотность газа? Проведем опыт. Уравновесим с помощью рычажных весов закрытую стеклянную колбу, помещенную внутрь сосуда (рис. 213, а), а затем вольем в этот сосуд углекислый газ (рис. 213, б). (Газы тоже можно переливать!) Так как плотность углекислого газа больше, чем воздуха, он вытеснит воздух из сосуда и займет его место. Равновесие весов нарушится (рис. 213, б), указывая на то, что в углекислом газе выталкивающая сила больше, чем в воздухе.
Следовательно, и в газах выталкивающая сила растет с увеличением плотности среды.
Почему возникает выталкивающая сила? Как ее рассчитать?
Для простоты расчетов рассмотрим погруженное в жидкость тело, имеющее форму прямоугольного параллелепипеда. Па рисунке 214 показаны силы, с которыми жидкость плотностью р действует на тело. Каждая из сил перпендикулярна к той поверхности, к которой она приложена.
Силы давления жидкости, действующие на боковые грани, только сжимают тело, но не выталкивают его. Выталкивающая сила возникает из-за того, что направленная вверх сила давления жидкости 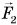 больше, чем сила
больше, чем сила 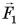 направленная вниз. В итоге модуль выталкивающей силы
направленная вниз. В итоге модуль выталкивающей силы

Из 7-го класса вы знаете, что сила давления F, с которой жидкость действует на поверхность площадью S, равна pS, где р — давление жидкости. Значит,
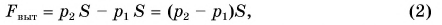
где р1 — давление на глубине 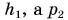 — на глубине h2(рис. 214). Вам известно также, что при увеличении глубины погружения на h давление возрастает на
— на глубине h2(рис. 214). Вам известно также, что при увеличении глубины погружения на h давление возрастает на 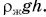 Тогда
Тогда

где 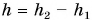 — это высота тела (рис. 214).
— это высота тела (рис. 214).
Из (2)и(3) следует
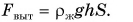
Но 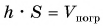 — объем погруженного тела. Следовательно:
— объем погруженного тела. Следовательно:
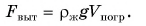
Произведение 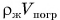 равно
равно 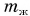 — массе жидкости, вытесненной телом при его погружении,
— массе жидкости, вытесненной телом при его погружении, 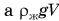 равно
равно 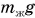 , т. е. весу вытесненной жидкости. В результате выталкивающая сила:
, т. е. весу вытесненной жидкости. В результате выталкивающая сила:

На тело, погруженное в жидкость (газ), действует выталкивающая сила, направленная вертикально вверх и равная весу жидкости (газа), вытесненной телом.
Это утверждение называют законом Архимеда а выталкивающую силу — силой Архимеда (и обозначают ее FA), по имени выдающегося древнегреческого ученого, открывшего данный закон за 250 лет до н. э.
Мы вывели формулу (4), рассматривая тело в форме параллелепипеда. Многочисленные опыты показывают: закон Архимеда применим к телам любой формы, погруженным в жидкость или газ полностью или частично.
Подчеркнем, что при частичном погружении тела в формуле (4) под объемом 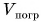 следует понимать объем погруженной в жидкость части тела.
следует понимать объем погруженной в жидкость части тела.
Теперь ответим еще на один вопрос. Почему тела, погруженные в жидкость, например в воду, ведут себя по-разному: одни из них (камни, металлические предметы) тонут, другие (куски дерева, пенопласта, пробки) плавают, частично погрузившись в воду, а третьи (рыбы, подводные лодки) плавают в толще воды?
Проведем опыт. Погрузим в стакан с соленой водой (рис. 215) кубики из сырого картофеля (1), пенопласта (2) и пластилина (3). Пластилиновый кубик опустится на дно, пенопластовый всплывет, а кубик из картофеля (при определенной концентрации соли в воде) останется внутри жидкости.
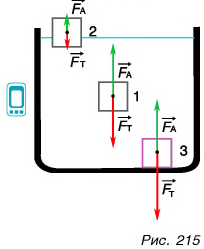
В чем причина этого различия? Все зависит от соотношения плотности тела и плотности жидкости. В нашем опыте плотность соленой воды 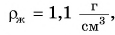 пластилина —
пластилина — 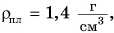 сырого картофеля —
сырого картофеля — 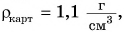 пенопласта —
пенопласта — 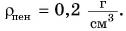
Сравнив плотность жидкости 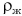 с плотностью тел
с плотностью тел 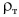 , сделаем вывод, что однородное тело:
, сделаем вывод, что однородное тело:
- при
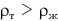 утонет в жидкости;
утонет в жидкости; - при
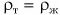 будет в состоянии равновесия на любой Рис. 215 глубине внутри жидкости;
будет в состоянии равновесия на любой Рис. 215 глубине внутри жидкости; - при
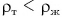 всплывет и будет находиться в состоянии равновесия, частично погрузившись в жидкость.
всплывет и будет находиться в состоянии равновесия, частично погрузившись в жидкость.
Объясните результаты опыта (рис. 215), сравнив силу тяжести FT каждого из тел с силой Архимеда FA.
Главные выводы:
- Выталкивающая сила (сила Архимеда) есть результат действия сил давления жидкости (газа) на погруженное тело.
- Закон Архимеда: «На тело, погруженное в жидкость (газ), действует выталкивающая сила, направленная вертикально вверх и равная весу жидкости (газа), вытесненной телом».
- Однородное тело тонет в жидкости, если плотность тела больше плотности жидкости, находится в равновесии внутри жидкости, если их плотности равны, и находится в состоянии равновесия, частично погрузившись в жидкость, если плотность тела меньше плотности жидкости.
Плавание судов. Воздухоплавание
На использовании силы Архимеда основано плавание плотов, лодок, кораблей, а также воздухоплавание. А что такое воздухоплавание? Чем оно отличается от полетов птиц, самолетов, ракет?
В предыдущем параграфе мы выяснили, что однородное тело, состоящее из вещества плотностью 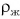 , не тонет в жидкости плотностью
, не тонет в жидкости плотностью 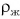 при условии
при условии 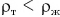 . А при каком условии будет плавать неоднородное тело, состоящее из материалов различной плотности (корабль, подводная лодка, катер)? При таком же условии, только вместо плотности вещества нужно взять среднюю плотность тела
. А при каком условии будет плавать неоднородное тело, состоящее из материалов различной плотности (корабль, подводная лодка, катер)? При таком же условии, только вместо плотности вещества нужно взять среднюю плотность тела 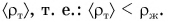
Среднюю плотность тела рассчитывают по формуле 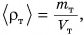 аналогичной формуле для плотности вещества. Средняя плотность тела зависит от плотности материалов, из которых оно состоит. Так, если из куска пластилина (рис. 216, а) слепить шар с воздушной полостью (рис. 216, б), то средняя плотность шара станет меньше плотности пластилина
аналогичной формуле для плотности вещества. Средняя плотность тела зависит от плотности материалов, из которых оно состоит. Так, если из куска пластилина (рис. 216, а) слепить шар с воздушной полостью (рис. 216, б), то средняя плотность шара станет меньше плотности пластилина 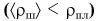 . А если заполнить полость свинцовой дробью (рис. 216, в)? Средняя плотность шара будет больше, чем плотность пластилина
. А если заполнить полость свинцовой дробью (рис. 216, в)? Средняя плотность шара будет больше, чем плотность пластилина 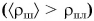 .
.

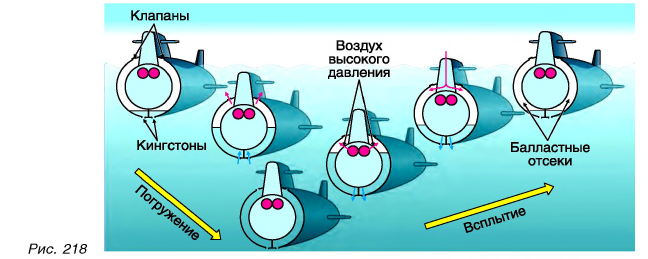
Корабли, паромы, яхты и т. д. конструируют так, чтобы их средняя плотность (р) была меньше плотности воды. В кораблях (рис. 217, a) для этого создают водонепроницаемые отсеки, заполненные воздухом. А для того чтобы подводная лодка (рис. 217, б) могла идти как в надводном, так и в подводном режиме, в ее конструкции (рис. 218) предусматривают возможность «управления» ее средней плотностью 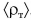 . Чтобы двигаться под водой, нужно увеличить среднюю плотность
. Чтобы двигаться под водой, нужно увеличить среднюю плотность 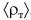 . Для этого специальные балластные отсеки лодки заполняют водой. Чтобы уменьшить среднюю плотность, воду из этих отсеков вытесняют сжатым воздухом (рис. 218).
. Для этого специальные балластные отсеки лодки заполняют водой. Чтобы уменьшить среднюю плотность, воду из этих отсеков вытесняют сжатым воздухом (рис. 218).
Для морских и речных судов существует максимальная глубина безопасного погружения. Ее называют предельной осадкой. Уровень погружения при предельной осадке отмечают па борту судна красной линией — ватерлинией (рис. 217, а).

Масса воды 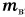 , вытесненной погруженным до ватерлинии судном, называется водоизмещением судна.
, вытесненной погруженным до ватерлинии судном, называется водоизмещением судна.
Знаменитый «Титаник» имел водоизмещение 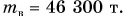
Осадка судна в незагруженном состоянии меньше предельной, а при наличии максимально допустимого груза — равна ей. Соответственно, масса корабля m без груза меньше его водоизмещения 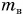 . Разность
. Разность 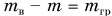 , равная массе максимально допустимого груза, называется грузоподъемностью судна. Современные морские танкеры, перевозящие нефть, имеют грузоподъемность 500 ООО т и больше.
, равная массе максимально допустимого груза, называется грузоподъемностью судна. Современные морские танкеры, перевозящие нефть, имеют грузоподъемность 500 ООО т и больше.
А что такое воздухоплавание? В отличие от авиации, в которой для полета используют устройства тяжелее воздуха (самолеты, вертолеты), воздухоплавание осуществляется с помощью таких летательных аппаратов, как воздушные шары, дирижабли и т. д.
Как и для плавания судов, основой воздухоплавания служит использование силы Архимеда.
Для любознательных:
Первый воздушный шар (рис. 219) был изобретен во Франции братьями Монгольфье и успешно запущен в 1782 г. Внизу шара было отверстие, под которым находилась жаровня с горячими углями. Воздух внутри шара постепенно нагревался, расширялся, и часть его уходила из шара. Его средняя плотность становилась меньше плотности воздуха снаружи, и шар поднимался вверх. Такие воздушные шары не могли подняться на большие высоты.

Как увеличить высоту подъема шара? Для этого современные шары наполняют не теплым воздухом, а гелием (его плотность примерно в 7 раз меньше плотности воздуха). Выталкивающая сила становится достаточной, чтобы шар с грузом мог подняться в стратосферу.
Разность между силой Архимеда и силой тяжести ненагруженного воздушного шара равна весу груза, который шар может поднять, т. е. его подъемной силе.
Почему летательные шары заполняют не водородом — самым легким из газов, а гелием? Потому, что водород (в отличие от гелия) образует с воздухом крайне взрывоопасную смесь!
Воздушные шары, поднимающиеся на сравнительно небольшие высоты, называются аэростатами, а на большие (более 11 км, где начинается стратосфера) — стратостатами. Аппараты, использующие в дополнение к силе Архимеда силу тяги двигателей, снабженных пропеллерами, называются дирижаблями (рис. 220).
Воздухоплавание нашло свое практическое применение. Запуская шары-зонды, снабженные датчиками, метеорологи получают информацию о температуре, давлении, о загрязненности атмосферы на различных высотах. Дирижабли применяются для перевозки крупногабаритных грузов.
Пользуются популярностью полеты на воздушных шарах в развлекательных целях (рис. 221).

Использование законов физики позволило человеку освоить воздушный и водный океаны. Воздух и вода — самые необходимые составляющие для жизни человека и всего живого мира. Поэтому осваивать воздушные и водные пространства надо экологически грамотно, стараясь не причинить им вреда.
Главные выводы:
- Плавание судов и воздухоплавание основаны на использовании выталкивающей силы (силы Архимеда).
- Масса воды, вытесненной погруженным до ватерлинии судном, называется водоизмещением судна.
- Грузоподъемность судна равна разности между водоизмещением и массой ненагруженного судна.
- Подъемная сила воздушного шара равна разности между силой Архимеда, действующей на него, и силой тяжести ненагруженного шара.
Пример №5
Площадь льдины S = 5,0 м2. На сколько увеличится глубина погружения льдины, если на нее ляжет морской котик массой m = 100 кг?
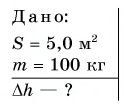
Решение
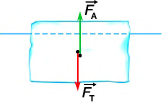
На льдину в воде действуют сила тяжести 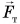 и сила Архимеда
и сила Архимеда 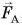 (рис. 222). В состоянии равновесия
(рис. 222). В состоянии равновесия 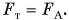 После того как на льдину ляжет морской котик, на нее подействует сила давления
После того как на льдину ляжет морской котик, на нее подействует сила давления 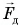 , равная весу
, равная весу 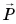 котика:
котика: 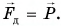 Льдина погрузится глубже в воду. При этом увеличится сила Архимеда, действующая на льдину:
Льдина погрузится глубже в воду. При этом увеличится сила Архимеда, действующая на льдину: 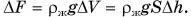 Увеличение силы Архимеда обусловлено весом морского котика:
Увеличение силы Архимеда обусловлено весом морского котика: 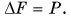 Так как
Так как 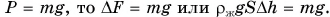 Отсюда
Отсюда

Ответ: 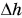 = 2 см.
= 2 см.
Элементы статики
Условия равновесия тела: 1. Векторная сумма сил, приложенных к телу, равна нулю. 2. Алгебраическая сумма моментов приложенных к телу сил равна нулю.
Изучение систем взаимодействующих частиц (абсолютно твердых тел) значительно упрощается, если рассматривать их поступательное и вращательное движения по отдельности.
Для рассмотрения динамики вращения необходимо определить физическую величину, представляющую собой «вращательный» аналог силы для поступательного движения и называемую моментом силы.
Эксперименты показывают, что в данном случае важна как точка приложения силы, так и направление ее действия относительно оси вращения. Для учета этих факторов вводится плечо силы, определяемое как кратчайшее расстояние от оси вращения (точка О на рисунке 45) до линии действия силы, т. е. длина перпендикуляра l, опущенного из точки О на линию действия силы 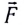 (см. рис. 45).
(см. рис. 45).
Момент силы М равен произведению модуля силы и ее плеча (см. рис. 45):
M = Fl. (1)
Основным результатом взаимодействия тел в динамике является возникновение ускорений. Из второго закона Ньютона следует, что под действием внешних сил и их моментов центр масс тела может перемещаться с некоторым ускорением и при этом тело может вращаться с угловым ускорением, причем ориентация этой оси может меняться с течением времени.
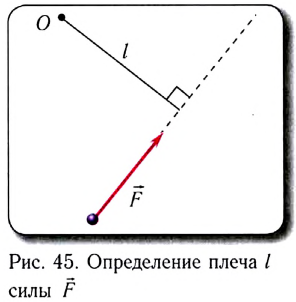
Движение замкнутой системы взаимодействующих частиц оказывается достаточно сложным. Однако в такой системе имеется точка, которая движется по прямой линии с постоянной скоростью. Эта точка называется центром масс и ее положение определяется выражением
Часто необходимо знать, при каких условиях тело, на которое действует несколько сил, покоится относительно некоторой инерциальной системы отсчета.
Существует область инженерной науки, изучающая условия равновесия твердых тел. Важно знать, какие силы необходимо приложить, чтобы удержать тело в состоянии покоя или предотвратить его разрушение.
Раздел механики, в котором изучаются условия равновесия, называется статикой.
Условия равновесия формулируются в статике для абсолютно твердого тела, т. е. тела, которое под действием внешних сил не деформируется.
Равновесным называется неизменное во времени состояние тела, т. е. равновесие — это такое состояние тела, при котором оно покоится (v = 0), движется равномерно 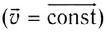 или вращается с постоянной угловой скоростью
или вращается с постоянной угловой скоростью 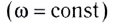 вокруг какой-либо оси, проходящей через центр масс.
вокруг какой-либо оси, проходящей через центр масс.
Название состояния равновесия произошло от латинского слова aequilibrium, означающего «равный» + «весы».
Для задания положения абсолютно твердого тела в данной инерциальной системе отсчета следует задать радиус-вектор 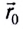 его центра масс, а также ориентацию тела (угол
его центра масс, а также ориентацию тела (угол 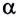 ) относительно центра масс (рис. 46).
) относительно центра масс (рис. 46).
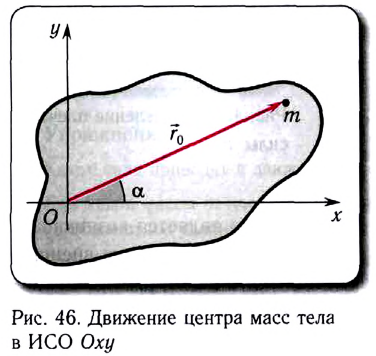
Если, например, твердое тело массой m может совершать движение в плоскости Оху выбранной системы отсчета под действием результирующей силы 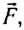 то для его равновесия (покоя) необходимо выполнение следующих двух условий.
то для его равновесия (покоя) необходимо выполнение следующих двух условий.
1. Для равновесия центра масс 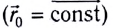 в инерциальной системе отсчета Оху необходимо:
в инерциальной системе отсчета Оху необходимо:
равенство нулю векторной суммы всех внешних сил, действующих на тело: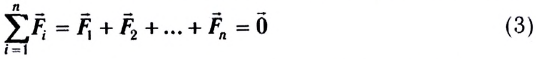
(сумма проекций внешних сил на любое направление также равна нулю).
2. Для постоянства угла ориентации (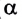 = const) необходимо:
= const) необходимо:
- равенство нулю алгебраической суммы моментов внешних сил относительно любой точки тела:
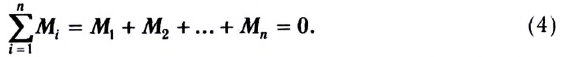
Моменты сил, вращающих тело против направления движения часовой стрелки, условно считают положительными, а по часовой — отрицательными.
Если оба условия выполняются для центра масс тела, то они выполняются и для любой точки этого тела.
При выполнении первого условия равновесия ускорение центра масс равно нулю, а при выполнении второго — равно нулю угловое ускорение. В случае если в начальный момент времени тело покоится, то оно будет оставаться в покое и в дальнейшем.
Отметим, что если тело не может вращаться, то для его равновесия достаточно выполнения первого условия. А если у тела есть закрепленная ось вращения, то для равновесия достаточно выполнения второго условия, так как приложенные силы можно разложить на составляющие, перпендикулярные и параллельные оси вращения. Составляющие сил, параллельные оси, не могут вращать тело вокруг нее. Вследствие этого они не будут оказывать никакого влияния на равновесие тела, они будут только деформировать ось и тело.
В обоих случаях одно из условий равновесия выполняется автоматически.
Отметим также, что необходимо, чтобы скорости всех точек тела в положении равновесия были равны нулю. Иначе тело будет с течением времени сдвигаться из положения равновесия.
В реальных условиях на любое тело действуют случайные внешние силы, которые отклоняют тело от положения равновесия. В новом положении условия равновесия нарушаются. Дальнейшее поведение тела зависит от того, в каком направлении действуют силы и моменты сил, возникающие при отклонении его от положения равновесия.
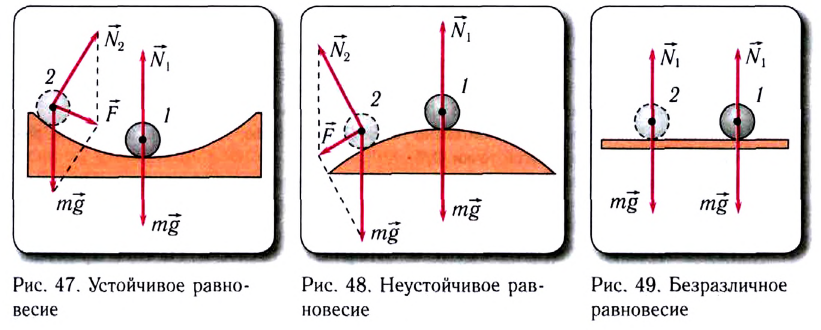
Равновесие называется устойчивым, если при малом отклонении тела от положения равновесия возникают силы и моменты сил, возвращающие его в исходное положение равновесия (рис. 47). Примером подобного равновесия служит равновесие шарика в ямке.
Равновесие называется неустойчивым, если силы и моменты сил, возникающие при малом отклонении тела от положения равновесия, вызывают дальнейшее отклонение тела от положения равновесия и оно не возвращается в исходное положение равновесия (рис. 48). Примером подобного равновесия служит равновесие шарика на вершине сферической горки.
Равновесие называется безразличным, если при отклонении тела от положения равновесия равнодействующая сила и момент сил остаются равными нулю (рис. 49). В этом случае новое положение тела также служит положением безразличного равновесия.
Условия равновесия с энергетической точки зрения
Закон сохранения механической энергии:
полная механическая энергия консервативной физической системы является величиной постоянной:
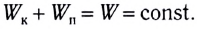
Рассмотрим условия равновесия шарика (см. рис. 47—49) с точки зрения закона сохранения энергии. Если трением и сопротивлением воздуха можно пренебречь, то полная механическая энергия шарика должна сохраняться:

В любом из трех положений 1 шарик обладает только потенциальной энергией. Поэтому увеличение кинетической энергии возможно лишь за счет уменьшения потенциальной.
Это означает, что в положении 1 шарика на рисунке 47 потенциальная энергия убывать не может, так как во всех ближайших точках (например, рис. 47, 2) она была бы больше, чем в исходном положении. Поэтому шарик будет сохранять это положение — устойчивого равновесия.
В положении 1 шарика на рисунке 48 потенциальная энергия убывать не может, так как в ближайших точках (например, рис. 48, 2) она будет меньше, чем в исходной. Поэтому при малейшем внешнем воздействии она будет убывать, превращаясь в кинетическую. Следовательно, равновесие неустойчивое.
В положении 1 шарика на рисунке 49 потенциальная энергия убывать не может, так как во всех ближайших точках (например, рис. 49, 2) она ничем не отличается от начальной. Поэтому равновесие безразличное.
Пусть положению равновесия 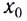 соответствует значение потенциальной энергии
соответствует значение потенциальной энергии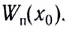 При перемещении шарика на расстояние
При перемещении шарика на расстояние 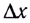 в направлении х сила F совершает работу
в направлении х сила F совершает работу 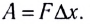 Эта работа совершается за счет уменьшения потенциальной энергии, т. е.
Эта работа совершается за счет уменьшения потенциальной энергии, т. е. 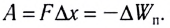 В положении равновесия
В положении равновесия 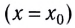
действующая на тело сила должна быть равна нулю. Это означает, что в положении равновесия потенциальная энергия должна иметь либо максимум, либо минимум. Если возникающая при отклонении от положения равновесия 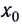 сила направлена к положению равновесия (см. рис. 47), то при удалении тела от этого положения она совершает отрицательную работу. Потенциальная энергия возрастает.
сила направлена к положению равновесия (см. рис. 47), то при удалении тела от этого положения она совершает отрицательную работу. Потенциальная энергия возрастает.
Следовательно, положению равновесия 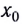 в этом случае соответствует минимум потенциальной энергии (рис. 50).
в этом случае соответствует минимум потенциальной энергии (рис. 50).
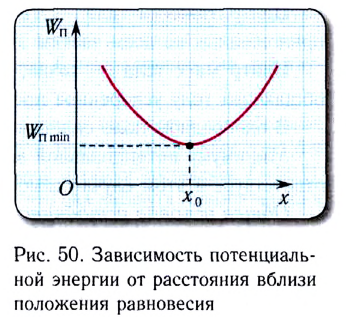
Если же возникающая сила направлена от положения равновесия 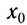 (см. рис. 48), то при удалении тела от этого положения она совершает положительную работу и потенциальная энергия уменьшается. Следовательно, положению равновесия в этом случае соответствует максимум потенциальной энергии.
(см. рис. 48), то при удалении тела от этого положения она совершает положительную работу и потенциальная энергия уменьшается. Следовательно, положению равновесия в этом случае соответствует максимум потенциальной энергии.
Таким образом, можно сформулировать следующие условия равновесия:
1. Равновесие устойчивое, если потенциальная энергия тела имеет минимальное из возможных ее значений:
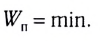
2. Равновесие неустойчивое, если потенциальная энергия тела имеет максимальное из возможных ее значений:
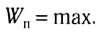
3. Равновесие безразличное, если потенциальная энергия тела имеет постоянное значение в данном его положении и в возможных ближайших положениях, т. е. не зависит от положения тела:
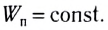
Отметим, что условие 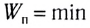 является общим условием устойчивости любой системы.
является общим условием устойчивости любой системы.
В общем, если система тел находится в равновесии и не получает энергию извне 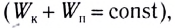 но тратит энергию, то движение в ней происходит так, что кинетическая энергия стремится к нулю
но тратит энергию, то движение в ней происходит так, что кинетическая энергия стремится к нулю  а потенциальная — к возможному наименьшему значению
а потенциальная — к возможному наименьшему значению 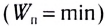 до тех пор, пока система не придет в состояние устойчивого равновесия.
до тех пор, пока система не придет в состояние устойчивого равновесия.
Отметим, что потенциальная энергия тела, находящегося в поле силы тяжести, определяется положением центра тяжести.
Центр тяжести тела — точка приложения равнодействующей сил тяжести, приложенных ко всем частям этого тела.
Центр масс тела — точка, через которую проходят линии действия сил, сообщающих телу ускоренное поступательное движение.
В однородном поле сил тяжести центр тяжести совпадает с центром масс. Минимуму потенциальной энергии и устойчивому положению равновесия со-
ответствует в этом случае самое низкое положение центра тяжести.
Общее условие устойчивого равновесия:
- центр тяжести тела, имеющего точку опоры, занимает самое низшее положение из всех возможных.
Этим условием удобно пользоваться при нахождении положения равновесия и исследовании характера равновесия.
Основные формулы
Модуль равнодействующей двух сил:
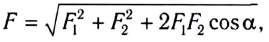
где 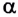 — угол между силами
— угол между силами 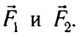
Первый закон Ньютона (закон инерции):
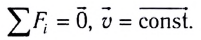
Второй закон Ньютона (основной закон динамики):
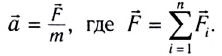
Третий закон Ньютона:
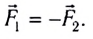
Закон всемирного тяготения:
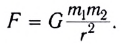
Закон Кулона—Амонтона:
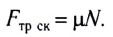
Сила вязкого трения при малых скоростях: 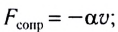 сила вязкого трения при больших скоростях:
сила вязкого трения при больших скоростях: 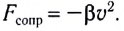
Закон Гука:
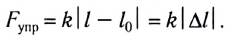
Жесткость k:
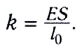
Момент силы:
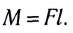
Первое условие равновесия:
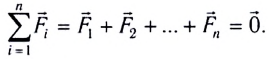
Второе условие равновесия:
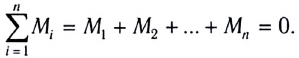
Ускорение свободного падения:
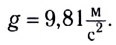
Гравитационная постоянная:
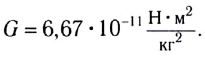
Скорость света в вакууме:
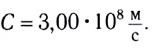
| Рекомендую подробно изучить предметы: |
| Ещё лекции с примерами решения и объяснением: |