
Способы преобразования чертежа в начертательной геометрии с примерами
Содержание:
Способы преобразования чертежа:
Способы преобразования чертежа применяются для приведения геометрических объектов в частное положение относительно плоскостей проекций, что позволяет упростить решение ряда позиционных и метрических задач.
Способы преобразования чертежа можно разделить на две группы.
- Способы дополнительного проецирования. Эти способы основаны на введении дополнительных плоскостей проекций и центров проецирования. При этом положение геометрических объектов по отношению к исходным плоскостям проекций
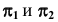
- Способы перемещения или вращения геометрических объектов.
Эти способы основаны на изменении положения геометрических объектов по отношению к исходным плоскостям проекций 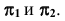
В данном пособии для примера рассмотрим способ дополнительного ортогонального проецирования.
Способ дополнительного ортогонального проецирования (ДОП)
Возьмем в пространстве дополнительную плоскость 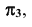 перпендикулярную плоскости
перпендикулярную плоскости 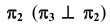 и составляющую с плоскостью
и составляющую с плоскостью 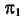 произвольный угол .
произвольный угол .
Проецирование на плоскость 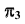 из несобственного центра
из несобственного центра 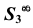 выберем ортогональным (аналогично проецированию на плоскости
выберем ортогональным (аналогично проецированию на плоскости 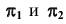 из соответствующих центров
из соответствующих центров 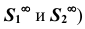 (рис. 81).
(рис. 81).
Для построения проекции 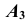 произвольной точки А исходного пространства выполним следующие операции:
произвольной точки А исходного пространства выполним следующие операции:
- через центр
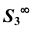 и точку А проведем прямую a;
и точку А проведем прямую a; - отметим точку пересечения прямой a с плоскостью
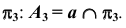
Полученная точка 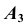 будет называться дополнительной ортогональной проекцией точки А на плоскость
будет называться дополнительной ортогональной проекцией точки А на плоскость 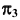 из центра
из центра 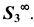
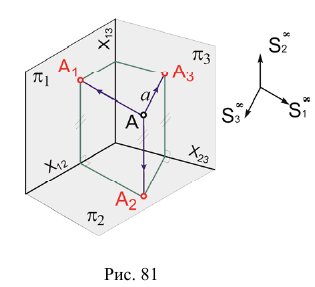
Из рис. 81 видно, что расстояние от точки A до плоскости равно расстоянию от точки
равно расстоянию от точки  до оси
до оси  а также расстоянию от точки
а также расстоянию от точки 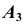 до оси
до оси 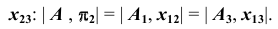
Для перехода к плоской модели повернем плоскость 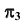 вокруг оси
вокруг оси 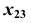 до совмещения с плоскостью
до совмещения с плоскостью 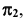 а затем — плоскость
а затем — плоскость 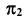 вокруг оси
вокруг оси 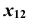 до совмещения с плоскостью
до совмещения с плоскостью 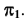
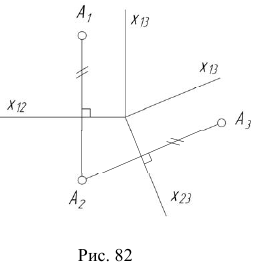
Положение проекции 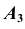 точки А на плоской модели определим следующим образом:
точки А на плоской модели определим следующим образом:
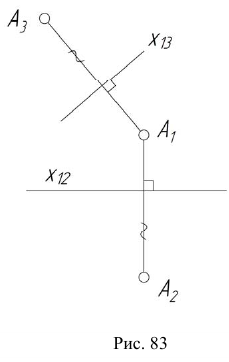
- из точки
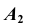 проведем линию связи перпендикулярно оси
проведем линию связи перпендикулярно оси 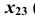 (рис. 82);
(рис. 82); - измерим расстояние от проекции
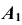 до оси
до оси 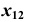 и отложим это значение по линии связи от оси
и отложим это значение по линии связи от оси 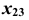 .
.
Если взять дополнительную плоскость 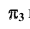 перпендикулярно плоскости
перпендикулярно плоскости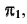 положение проекции
положение проекции 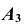 на плоской модели определится следующим образом:
на плоской модели определится следующим образом:
- из точки
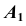 проведем линию связи перпендикулярно прямой
проведем линию связи перпендикулярно прямой 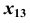 (рис. 83);
(рис. 83); - измерим расстояние от проекции
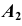 до оси
до оси 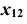 и отложим это значение по линии связи от оси
и отложим это значение по линии связи от оси 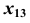 .
.
Решение позиционных и метрических задач способом ДОП
Рассмотрим ряд задач, связанных с приведением геометрических объектов в частное положение относительно плоскостей проекций и определением некоторых метрических характеристик этих объектов способом ДОП.
Задача:
Преобразовать прямую общего положения m в прямую уровня. Для решения этой задачи дополнительная плоскость проекций 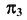 выбирается параллельно прямой m и перпендикулярно одной из плоскостей проекций. Если
выбирается параллельно прямой m и перпендикулярно одной из плоскостей проекций. Если 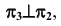 на плоской модели ось
на плоской модели ось 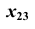 будет параллельна
будет параллельна 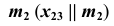 (рис. 84).
(рис. 84).
Алгоритм решения
- Проведем ось
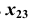 параллельно проекции
параллельно проекции 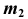 на произвольном расстоянии от нее.
на произвольном расстоянии от нее. - Отметим на прямой m две точки —
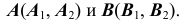
- Определим проекции
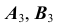 точек A и B в дополнительном поле проекций
точек A и B в дополнительном поле проекций 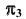 в соответствии с рис. 82.
в соответствии с рис. 82.
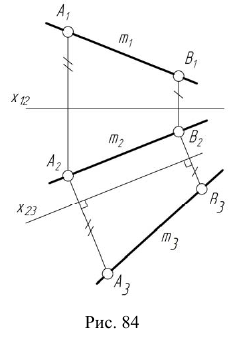
В новой системе плоскостей 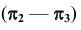 прямая
прямая 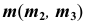 преобразуется в линию уровня.
преобразуется в линию уровня.
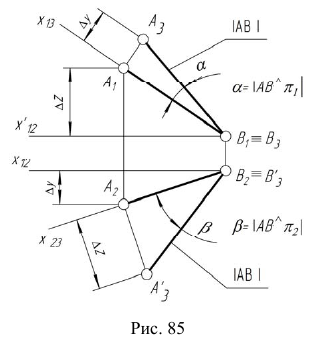
Используя это преобразование можно измерить длину отрезка AB , а также углы между отрезком и плоскостями проекций (рис. 85).
Задача:
Преобразовать прямую уровня h в проецирующую прямую (рис. 86).
Для решения этой задачи дополнительная плоскость 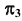 выбирается перпендикулярно прямой. Так как по условию задачи прямая h параллельна плоскости
выбирается перпендикулярно прямой. Так как по условию задачи прямая h параллельна плоскости 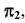 очевидно, что плоскость
очевидно, что плоскость 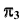 будет перпендикулярна горизонтальной плоскости проекций, а на плоской модели ось
будет перпендикулярна горизонтальной плоскости проекций, а на плоской модели ось 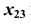 перпендикулярна
перпендикулярна 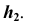
Алгоритм решения
- Проведем ось
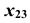 перпендикулярно проекции
перпендикулярно проекции 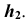
- Отметим на прямой h две точки —
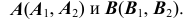
- Определим проекции
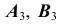 точек A и B в дополнительном поле проекций
точек A и B в дополнительном поле проекций 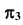 в соответствии с рис. 82.
в соответствии с рис. 82.
В новой системе плоскостей  прямая
прямая 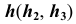 преобразуется в проецирующую прямую.
преобразуется в проецирующую прямую.
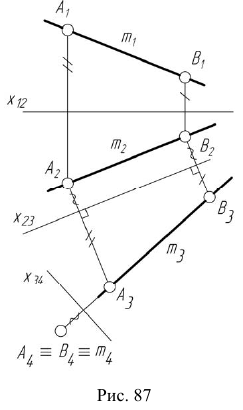
Преобразование прямой общего положения в проецирующую прямую осуществляется в два этапа. На первом этапе прямая общего положения преобразуется в прямую уровня (задача 11). Затем при введении еще одной дополнительной плоскости — 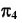 прямая уровня преобразуется в проецирующую прямую (задача 12). На рис. 87 приведен пример преобразования прямой общего положения m в проецирующую.
прямая уровня преобразуется в проецирующую прямую (задача 12). На рис. 87 приведен пример преобразования прямой общего положения m в проецирующую.
Для построения проекций точек в поле 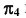 измерим расстояния в поле проекций
измерим расстояния в поле проекций 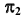 (от точек
(от точек 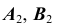 до оси
до оси 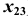 ) и отложим его в поле
) и отложим его в поле 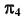 от оси
от оси 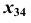 по линии проекционной связи, перпендикулярной
по линии проекционной связи, перпендикулярной 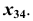
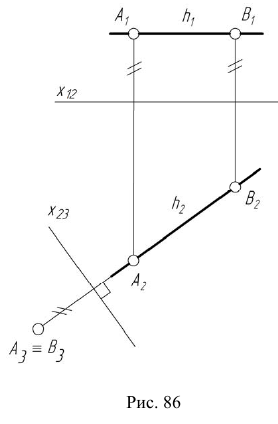
Задача:
Преобразовать плоскость 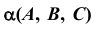 общего положения в проецирующую (рис. 88).
общего положения в проецирующую (рис. 88).
Исходя из определения проецирующей плоскости дополнительная плоскость проекций 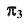 должна быть перпендикулярна прямой, принадлежащей этой плоскости. Учитывая, что дополнительная плоскость перпендикулярна
должна быть перпендикулярна прямой, принадлежащей этой плоскости. Учитывая, что дополнительная плоскость перпендикулярна 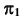 или
или 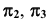 выберем перпендикулярно фронтали или горизонтали плоскости
выберем перпендикулярно фронтали или горизонтали плоскости 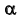 соответственно.
соответственно.
Возьмем плоскость 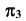 перпендикулярно горизонтали h плоскости
перпендикулярно горизонтали h плоскости 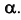 Очевидно, что при этом плоскость
Очевидно, что при этом плоскость 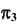 будет перпендикулярна горизонтальной плоскости проекций, а на плоской модели ось
будет перпендикулярна горизонтальной плоскости проекций, а на плоской модели ось 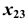 перпендикулярна
перпендикулярна 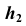 (см. рис. 88).
(см. рис. 88).
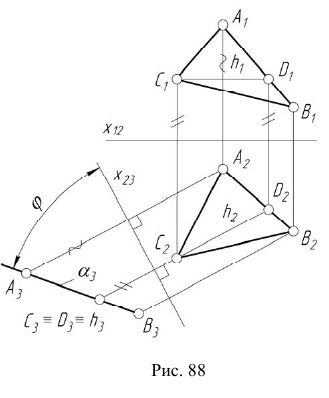
Алгоритм решения
- Построим горизонталь
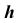
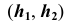 плоскости
плоскости 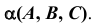
- Проведем ось
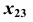 перпендикулярно проекции
перпендикулярно проекции 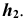
- Определим проекции горизонтали h и точки A в дополнительном поле проекций
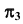 — совпавшие проекции
— совпавшие проекции 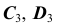 и проекцию
и проекцию 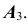
- Через точки
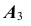 и
и 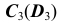 проведем прямую
проведем прямую 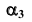 — вырожденную проекцию плоскости.
— вырожденную проекцию плоскости.
В новой системе плоскостей 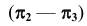 плоскость
плоскость 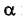 преобразуется в проецирующую плоскость.
преобразуется в проецирующую плоскость.
Используя это преобразование можно измерить угол 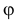 между плоскостью общего положения
между плоскостью общего положения 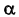 и плоскостью проекций
и плоскостью проекций 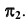 Для определения угла между плоскостью общего положения и плоскостью
Для определения угла между плоскостью общего положения и плоскостью 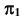 дополнительную плоскость
дополнительную плоскость 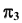 нужно задать перпендикулярно фронтали плоскости
нужно задать перпендикулярно фронтали плоскости 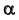 и выполнить аналогичные преобразования.
и выполнить аналогичные преобразования.
На рис. 89 приведен пример использования способа ДОП для построения линии пересечения поверхности общего положения 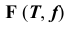 с плоскостью общего положения
с плоскостью общего положения 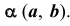 Преобразование плоскости общего положения в проецирующую позволит в данной задаче определить характер линии пересечения и точно построить ее экстремальную точку.
Преобразование плоскости общего положения в проецирующую позволит в данной задаче определить характер линии пересечения и точно построить ее экстремальную точку.
Для преобразования плоскости 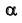 в проецирующую определим
в проецирующую определим 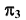 перпендикулярной горизонтали b плоскости
перпендикулярной горизонтали b плоскости 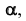 следовательно, на плоской модели ось
следовательно, на плоской модели ось 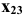 будет перпендикулярна
будет перпендикулярна 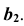
При таком преобразовании чертежа очерк конической поверхности в поле 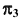 будет таким же, как и в поле
будет таким же, как и в поле 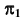 (см. рис. 89, а). По проекциям конической поверхности и плоскости
(см. рис. 89, а). По проекциям конической поверхности и плоскости 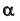 в поле
в поле 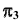 видно, что сечение представляет собой параболу с вершиной в точке A.
видно, что сечение представляет собой параболу с вершиной в точке A.
Далее в системе плоскостей 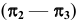 строим горизонтальную проекцию
строим горизонтальную проекцию 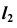 параболы (см. рис. 89, б). При построении фронтальной проекции
параболы (см. рис. 89, б). При построении фронтальной проекции 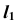 (см. рис. 89, в) используем расстояния от оси
(см. рис. 89, в) используем расстояния от оси 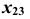 до соответствующих проекций точек линии сечения в поле
до соответствующих проекций точек линии сечения в поле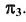 Проекцию
Проекцию 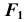 точки изменения видимости параболы при проецировании на плоскость
точки изменения видимости параболы при проецировании на плоскость 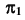 определим на фронтальном очерке
определим на фронтальном очерке 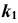 конической поверхности.
конической поверхности.
Задача:
Преобразовать проецирующую плоскость 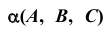 в плоскость уровня. Исходя из определения плоскости уровня дополнительная плоскость проекций
в плоскость уровня. Исходя из определения плоскости уровня дополнительная плоскость проекций 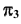 должна быть параллельна плоскости
должна быть параллельна плоскости 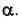 Так как плоскость
Так как плоскость 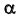 по условию задачи является фронтально-проецирующей (рис. 90), очевидно, что плоскость
по условию задачи является фронтально-проецирующей (рис. 90), очевидно, что плоскость 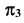 будет перпендикулярна фронтальной плоскости проекций, а на плоской модели ось
будет перпендикулярна фронтальной плоскости проекций, а на плоской модели ось 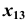 параллельна
параллельна 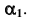
Алгоритм решения
- Проведем ось
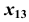 параллельно проекции
параллельно проекции 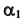 на произвольном расстоянии от нее.
на произвольном расстоянии от нее. - Определим проекции
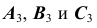 точек A, B и С в дополнительном поле проекций
точек A, B и С в дополнительном поле проекций 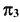 в соответствии с рис. 83.
в соответствии с рис. 83.
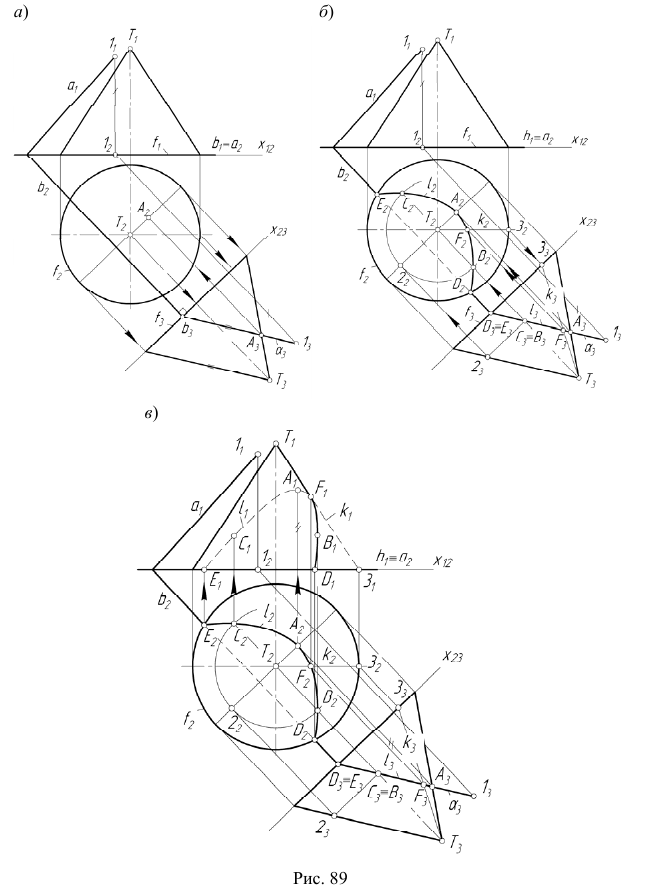
В новой системе плоскостей  плоскость
плоскость 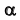 преобразовалась в плоскость уровня. По проекции треугольника в поле
преобразовалась в плоскость уровня. По проекции треугольника в поле 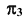 можно определить все его метрические характеристики.
можно определить все его метрические характеристики.
Это преобразование используется в практике черчения для построения натуральной величины наклонного сечения детали. На рис. 91 приведен пример построения натуральной величины ортогонального сечения прямого кругового конуса плоскостью 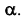
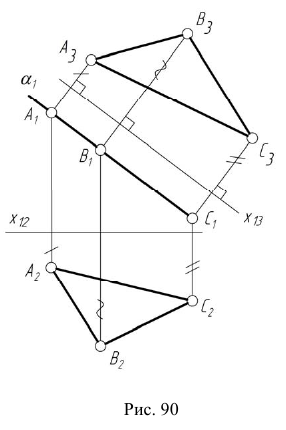
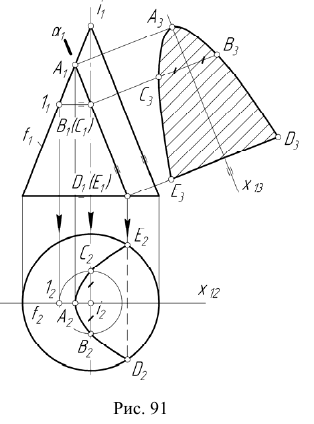
Преобразование плоскости общего положения в плоскость уровня осуществляется в два этапа. На первом этапе плоскость общего положения преобразуется в проецирующую (задача 13). Затем, при введении еще одной дополнительной плоскости — 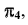 проецирующая плоскость преобразуется в плоскость уровня (задача 14).
проецирующая плоскость преобразуется в плоскость уровня (задача 14).
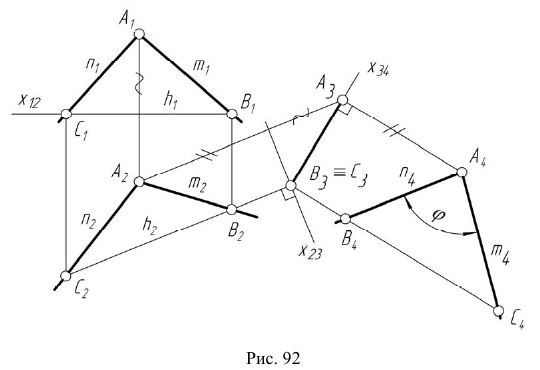
На рис. 92 приведен пример преобразования плоскости общего положения в плоскость уровня. Используя это преобразование, можно определить угол между пересекающимися прямыми m и n.
Если плоскость общего положения будет задана некоторой фигурой 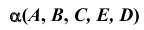 (рис. 93), то подобное преобразование позволит определить размеры и форму плоской фигуры.
(рис. 93), то подобное преобразование позволит определить размеры и форму плоской фигуры.
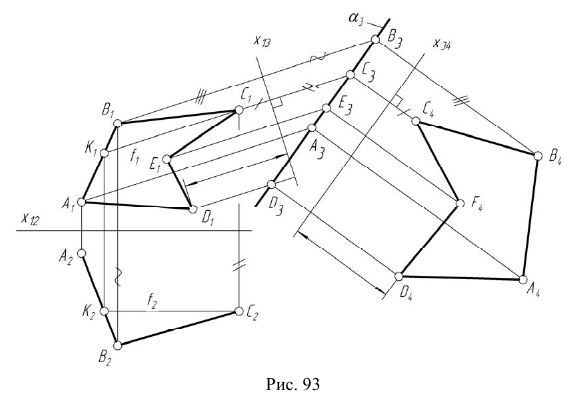
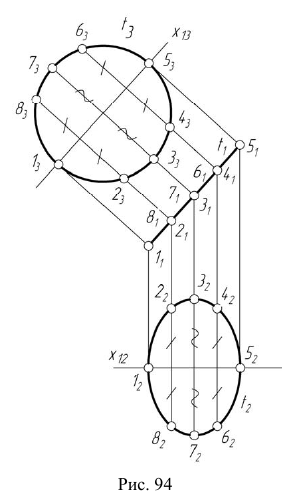
Рассмотрим пример использования способа ДОП для построения горизонтальной проекции окружности t по ее вырожденной фронтальной проекции 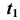 и проекции
и проекции 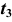 (рис. 94).
(рис. 94).
Так как плоскость окружности по условию задачи является фронтально- проецирующей, очевидно, что на плоской модели ось 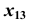 будет параллельна
будет параллельна 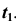 .
.
В качестве оси отсчета 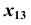 возьмем прямую, проходящую через центр окружности
возьмем прямую, проходящую через центр окружности 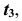 , а ось отсчета
, а ось отсчета 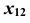 — в произвольном месте чертежа (рис. 94). Для построения горизонтальных проекций точек окружности измерим расстояния от оси
— в произвольном месте чертежа (рис. 94). Для построения горизонтальных проекций точек окружности измерим расстояния от оси 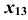 до проекций точек в поле
до проекций точек в поле 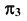 и отложим эти расстояния на соответствующих линиях проекционной связи от оси
и отложим эти расстояния на соответствующих линиях проекционной связи от оси 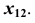
Способы преобразования проекционного чертежа. Способ замены плоскостей проекций
Решение многих пространственных задач как позиционных, так и метрических на эпюре Монжа часто усложняется из-за того, что геометрические объекты (оригиналы) произвольно расположены в пространстве относительно плоскостей проекций и, следовательно, проецируются на них с искажением. В связи с этим, естественно, появляется мысль о целесообразности замены данной системы взаимно перпендикулярных плоскостей проекций 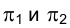 новой системой, выбранной так, чтобы неподвижный объект в пространстве оказался в каком-либо частном положении относительно этой новой системы.
новой системой, выбранной так, чтобы неподвижный объект в пространстве оказался в каком-либо частном положении относительно этой новой системы.
Например, прямые общего положения в старой системе плоскостей проекций в новой становятся прямыми частного положения, плоскости общего положения в старой системе плоскостей проекций в новой становятся проецирующими и т.д.
Для решения ряда задач бывает достаточно заменить лишь одну из старых плоскостей проекций, решение других требует последовательной замены обеих плоскостей проекций старой системы новыми. Однако следует обязательно подчеркнуть, что при всех условиях должна быть соблюдена взаимная перпендикулярность плоскостей проекций в исходной (старой) и последующих (новых) системах.
Естественно задать вопрос: "А какой же геометрической информацией следует располагать, чтобы построить изображение исследуемого геометрического образа на некоторой новой плоскости проекций, заменившей одну из старых?"
Рассмотрим систему плоскостей проекций 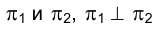 и определим в ней положение некоторой точки М, построив ее ортогональные проекции
и определим в ней положение некоторой точки М, построив ее ортогональные проекции 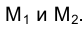
Перейдем от системы плоскостей проекций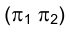 к новой системе, составленной из горизонтальной плоскости проекций
к новой системе, составленной из горизонтальной плоскости проекций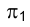 и перпендикулярной к ней новой плоскости проекций
и перпендикулярной к ней новой плоскости проекций 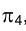 , введенной взамен плоскости
, введенной взамен плоскости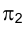 (рис. 2.1). (Здесь и далее индексация вновь вводимых плоскостей проекций
(рис. 2.1). (Здесь и далее индексация вновь вводимых плоскостей проекций 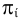 начинается с цифры 4, поскольку цифра 3 в обозначении плоскости проекций соответствует профильной плоскости). Заменив плоскость
начинается с цифры 4, поскольку цифра 3 в обозначении плоскости проекций соответствует профильной плоскости). Заменив плоскость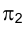 на
на 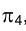 , построим ортогональную проекцию на ней точки
, построим ортогональную проекцию на ней точки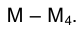
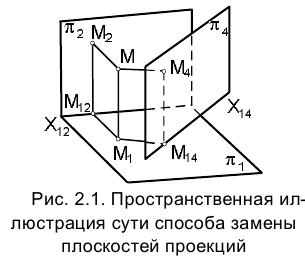
Очевидно, что в новой системе плоскостей проекций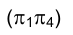 положение точки М в пространстве также однозначно определяется ее проекциями
положение точки М в пространстве также однозначно определяется ее проекциями 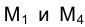 , как в старой системе плоскостей проекций
, как в старой системе плоскостей проекций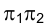 проекциями
проекциями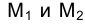 , и естественно поэтому рассматривать обе эти системы как совершенно равноправные. Из рис. 2.1 видно, что в пространстве расстояние от точки М до горизонтальной плоскоcти проекций p1 может бить измерено длиной равных между собой отрезков
, и естественно поэтому рассматривать обе эти системы как совершенно равноправные. Из рис. 2.1 видно, что в пространстве расстояние от точки М до горизонтальной плоскоcти проекций p1 может бить измерено длиной равных между собой отрезков 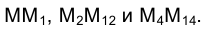
Рассмотрим теперь, как осуществляется переход от системы плоскостей проекции 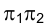 к системе
к системе 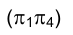 на эпюре Монжа. В соответствии с принципом образования эпюра Монжа (см. раз- дел 1) совместим плоскости проекций
на эпюре Монжа. В соответствии с принципом образования эпюра Монжа (см. раз- дел 1) совместим плоскости проекций 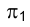 и
и 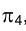 с плоскостью
с плоскостью 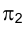 последовательными поворотами относительно осей проекций
последовательными поворотами относительно осей проекций 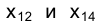 (рис. 2.2, 2.3). На основании отмеченного выше следует, что проекции
(рис. 2.2, 2.3). На основании отмеченного выше следует, что проекции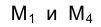 точки располагаются на перпендикуляре к новой оси проекций
точки располагаются на перпендикуляре к новой оси проекций 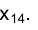
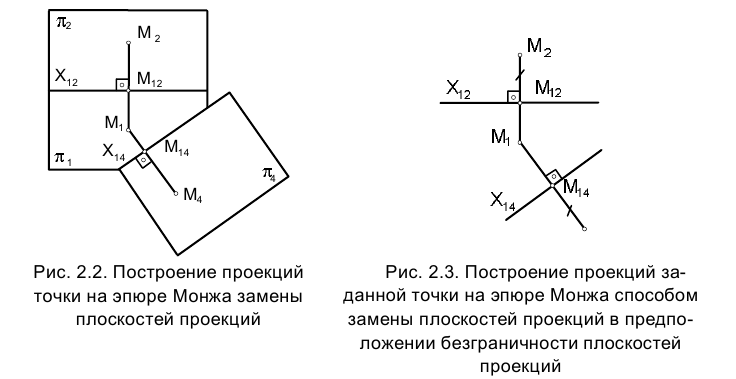
Кроме того, расстояние от проекции 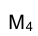 точки М до новой оси проекции
точки М до новой оси проекции 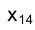 равно расстоянию от проекции
равно расстоянию от проекции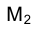 точки М до старой оси проекций
точки М до старой оси проекций 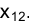 , поскольку оба они равны расстоянию от точки М в пространстве до горизонтальной плоскости проекций
, поскольку оба они равны расстоянию от точки М в пространстве до горизонтальной плоскости проекций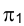 (см. рис. 2.1).
(см. рис. 2.1).
Следовательно, для построения на эпюре Монжа новой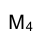 проекции точки М, заданной своими ортогональными
проекции точки М, заданной своими ортогональными 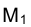 и
и 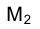 проекциями на плоскостях
проекциями на плоскостях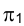 и
и 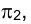 , нужно через горизонтальную проекцию точки М -
, нужно через горизонтальную проекцию точки М - 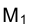 провести перпендикуляр к новой оси проекций
провести перпендикуляр к новой оси проекций 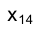 и от точки их пересечения отложить на нем отрезок, равный расстоянию от фронтальной проекции точки М -
и от точки их пересечения отложить на нем отрезок, равный расстоянию от фронтальной проекции точки М - 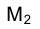 до старой оси проекций
до старой оси проекций 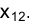 . Если плоскость
. Если плоскость 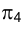 перпендикулярна фронтальной плоскости проекций
перпендикулярна фронтальной плоскости проекций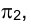 , то перпендикуляр к новой оси проекций определяет направление линии связи в новой системе плоскостей проекций.
, то перпендикуляр к новой оси проекций определяет направление линии связи в новой системе плоскостей проекций.
Таким образом, ответ на поставленный в начале параграфа, вопрос состоит в том, что для построения изображения исследуемого геометрического образа на некоторой новой плоскости проекций (например 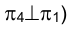 следует располагать геометрической информацией о его положении относительно незаменяемой - общей для обеих систем плоскостей проекций новой
следует располагать геометрической информацией о его положении относительно незаменяемой - общей для обеих систем плоскостей проекций новой 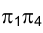 и старой
и старой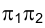 плоскости
плоскости 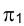 .
.
В рассматриваемом случае построения точки М информацией является ее отстояние от плоскости 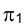 .
.
Отмеченное выше позволяет утверждать, что при построении на новой плоскости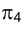 новой проекции
новой проекции 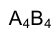 некоторого отрезка прямой АВ (рис. 2.4) разность удалений концов этого отрезка от плоскости
некоторого отрезка прямой АВ (рис. 2.4) разность удалений концов этого отрезка от плоскости 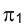 измеряется равными расстояниями на плоскостях проекций
измеряется равными расстояниями на плоскостях проекций 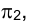 и
и 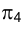 , т.е.
, т.е. 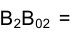
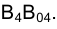 . Аналогичный вывод будет справедлив и в случае
. Аналогичный вывод будет справедлив и в случае 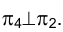
При решении многих задач, связанных с определением истинной формы плоского геометрического образа, сложность состоит в том, что исследуемый объект расположен в плоскости общего положения по отношению к системе плоскостей проекций 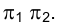
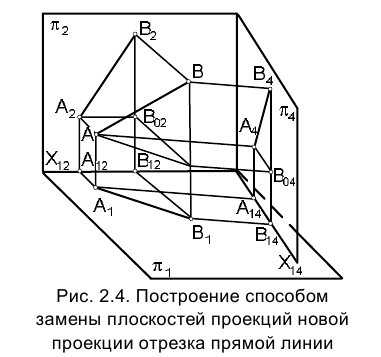
Поэтому важно так выбрать новую систему плоскостей проекций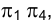 , чтобы по отношению к одной из них исследуемый объект стал проецирующим, что позволит в дальнейшем определить его истинную форму.
, чтобы по отношению к одной из них исследуемый объект стал проецирующим, что позволит в дальнейшем определить его истинную форму.
Рассмотрим в качестве примера, плоские боковые кили судна, являющиеся пассивными успокоителями качки (рис. 2.5). Плоскость каждого такого киля - это плоскость общего положения в системе плоскостей проекций 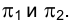
Зададим плоскость бокового киля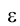 треугольником МNР (рис. 2.6) и заменим плоскость
треугольником МNР (рис. 2.6) и заменим плоскость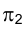 новой плоскостью проекций
новой плоскостью проекций 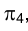 , перпендикулярной плоскостям
, перпендикулярной плоскостям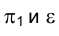 одновременно.
одновременно.
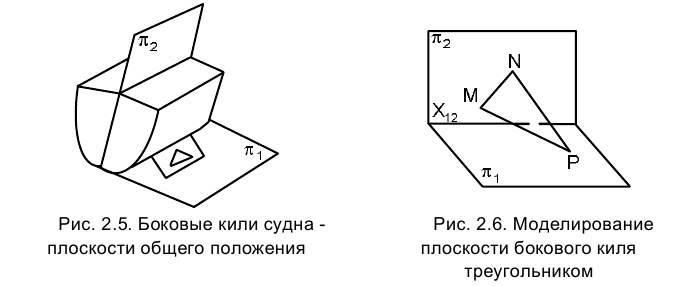
На плоскости  плоскость
плоскость изобразится отрезком прямой линии
изобразится отрезком прямой линии 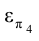 , т.е. станет плоскостью фронтально проецирующей по отношению к
, т.е. станет плоскостью фронтально проецирующей по отношению к  .
.
На рис. 2.7 иллюстрируется переход от системы плоскостей проекций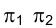 к системе, в которой плоскость
к системе, в которой плоскость 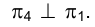 . Заметим, что плоскостей, перпендикулярных к плоскости
. Заметим, что плоскостей, перпендикулярных к плоскости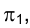 , бесчисленное множество и среди них следует определить плоскость
, бесчисленное множество и среди них следует определить плоскость  , одновременно перпендикулярную к плоскости
, одновременно перпендикулярную к плоскости . Для того, чтобы выделить такую плоскость
. Для того, чтобы выделить такую плоскость , следует сформулировать критерий перпендикулярности ее и плоскости
, следует сформулировать критерий перпендикулярности ее и плоскости 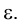
Плоскость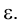 будет перпендикулярна плоскости
будет перпендикулярна плоскости  , если она проходит через некоторую прямую, перпендикулярную
, если она проходит через некоторую прямую, перпендикулярную  .Учитывая, что
.Учитывая, что 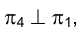 , такой прямой является произвольная горизонталь h плоскости
, такой прямой является произвольная горизонталь h плоскости 
На эпюре Монжа горизонтальная проекция горизонтали определит направление линии связи точек в системе плоскостей проекций 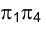 (рис. 2.8).
(рис. 2.8).
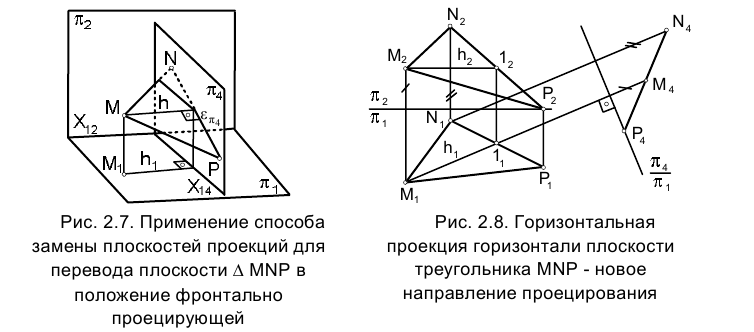
Итак, рассмотрим алгоритм, реализующий на эпюре Монжа перевод плоскости  в положение фронтально проецирующей. Новое направление линии связи в системе плоскостей проекций
в положение фронтально проецирующей. Новое направление линии связи в системе плоскостей проекций 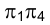 определится горизонтальной проекцией горизонтали
определится горизонтальной проекцией горизонтали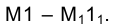
Произвольная прямая, проведенная перпендикулярно направлению линии связи, будет параллельна направлению оси проекций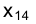 и может быть использована в качестве так называемой линии отсчета, для того чтобы отложить соответствующие разности удалений вершин треугольника МNР от горизонтальной плоскости проекций
и может быть использована в качестве так называемой линии отсчета, для того чтобы отложить соответствующие разности удалений вершин треугольника МNР от горизонтальной плоскости проекций 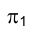 и построить его проекцию на плоскости
и построить его проекцию на плоскости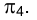 .
.
В качестве линии отсчета в системе плоскостей проекций 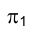 и
и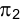 может быть использована произвольная прямая, параллельная направлению оси проекций
может быть использована произвольная прямая, параллельная направлению оси проекций 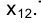 .То, что треугольник МNР изобразится на плоскости
.То, что треугольник МNР изобразится на плоскости 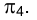 в виде отрезка прямой, следует из самой постановки задачи, поэтому принадлежность точек
в виде отрезка прямой, следует из самой постановки задачи, поэтому принадлежность точек 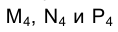 этому отрезку характеризует графическую точность решения.
этому отрезку характеризует графическую точность решения.
Аналогичные рассуждения приводят к выводу, что для перевода способом замены плоскостей проекций плоскости общего положения в горизонтально проецирующую следует в качестве нового направления проецирования принять направление фронтальной проекции ее фронтали.
Способ вращения вокруг осей, перпендикулярных и параллельных плоскостям проекций
Если способ замены плоскостей проекций позволяет разместить новую плоскость проекций в пространстве наиболее удачно по отношению к неподвижному объекту и затем проанализировать на ней его геометрические свойства, то существо применяемых способов вращения объектов наоборот состоит в том, чтобы, повернув их в некоторое определенное по отношению к неподвижным плоскостям проекций положение, в дальнейшем наиболее удачно решить поставленную задачу.
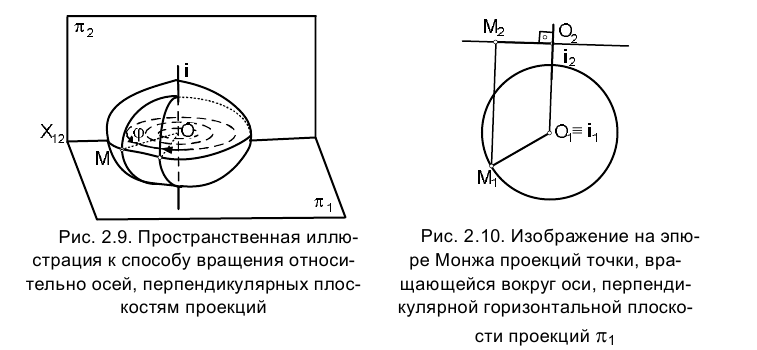
Вращение вокруг оси, перпендикулярной к плоскости проекций На рис. 2.9 заданы ортогональные проекции точки М и прямой ί, перпендикулярной горизонтальной плоскости проекций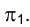 .
.
Будем считать, что точка М и прямая ί принадлежат твердому телу, т.е. телу, расстояние между любыми двумя точками которого неизменно.
Если внутри твердого тела провести две прямые, то в процессе его движения ни угол между этими прямыми, ни расстояние между ними не изменяются.
Назовем прямую ί осью вращения и представим себе, что твердое тело, которому принадлежит точка М, поворачивается вокруг нее. При этом точка М будет перемещаться по окружности, плоскость которой перпендикулярна оси вращения (рис. 2.10), а центр расположен на этой оси. Точка М, естественно, располагается на перпендикуляре к оси вращения. Поскольку в рассматриваемом случае ось вращения ί, перпендикулярна плоскости 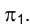 , то горизонтальная проекция точки М –
, то горизонтальная проекция точки М –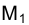 опишет окружность с центром в точке
опишет окружность с центром в точке 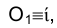 , а точка
, а точка 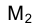 будет перемещаться по прямой, перпендикулярной фронтальной проекции
будет перемещаться по прямой, перпендикулярной фронтальной проекции 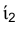 оси вращения.
оси вращения.
Можно поэтому сформулировать следующее положение: при вращении точки вокруг оси, перпендикулярной плоскости проекций 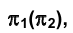 , горизонтальная (фронтальная) проекция точки описывает окружность с центром в горизонтальной (фронтальной) проекции оси вращения, а фронтальная (горизонтальная)проекция точки движется по прямой, перпендикулярной направлению линии связи.
, горизонтальная (фронтальная) проекция точки описывает окружность с центром в горизонтальной (фронтальной) проекции оси вращения, а фронтальная (горизонтальная)проекция точки движется по прямой, перпендикулярной направлению линии связи.
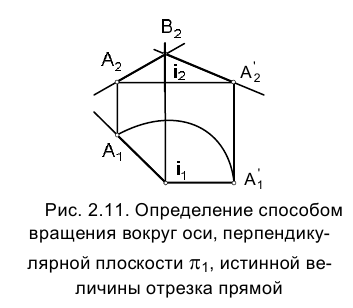
Определим истинную величину отрезка АВ прямой линии а (рис. 2.11). Выберем ось вращения, проходящую через точку 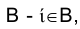
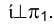 Повернем отрезок в положение, параллельное фронтальной плоскости проекций
Повернем отрезок в положение, параллельное фронтальной плоскости проекций 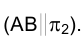 . Наметим направление горизонтальной проекции
. Наметим направление горизонтальной проекции 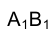 отрезка АВ после поворота.
отрезка АВ после поворота.
Направление прямой а должно быть таким, чтобы горизонтальная проекция отрезка АВ–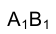 располагалась перпендикулярно направлению линии связи.
располагалась перпендикулярно направлению линии связи.
Тогда фронтальная проекция отрезка АВ – 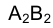 определит его истинную величину.
определит его истинную величину.
Рассмотрим поворот на некоторый угол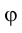 треугольника KLM (плоской фигуры) вокруг оси ί, перпендикулярной фронтальной плоскости проекций
треугольника KLM (плоской фигуры) вокруг оси ί, перпендикулярной фронтальной плоскости проекций 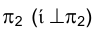 и проходящей через вершину М (рис. 2.12, 2.13).
и проходящей через вершину М (рис. 2.12, 2.13).
В пространстве каждая точка плоскости треугольника КLМ опишет дугу окружности, плоскость которой параллельна фронтальной плоскости проекций 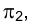 , а центр принадлежит оси ί. Следовательно, фронтальные проекции точек, принадлежащих треугольнику KLМ, будут перемещаться по дугам концентрических окружностей с центром в точке
, а центр принадлежит оси ί. Следовательно, фронтальные проекции точек, принадлежащих треугольнику KLМ, будут перемещаться по дугам концентрических окружностей с центром в точке 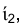 , а их горизонтальные проекции будут перемещаться по прямым, перпендикулярным направлению линии связи.
, а их горизонтальные проекции будут перемещаться по прямым, перпендикулярным направлению линии связи.
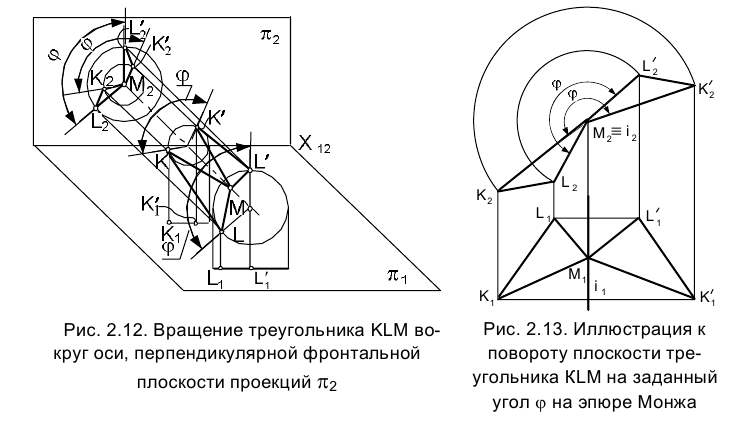
Отмеченный на рис. 2.12 угол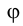 является линейным углом двугранного угла, образованного плоскостью, проходящей через ось вращения ί и точку К, с плоскостью, проходящей через ту же ось и новое положение точки К. Угол
является линейным углом двугранного угла, образованного плоскостью, проходящей через ось вращения ί и точку К, с плоскостью, проходящей через ту же ось и новое положение точки К. Угол 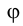 характеризует поворот всего твердого тела, которому принадлежат треугольник КLМ и ось вращения ί, и поэтому называется углом поворота. На такой же угол повернется любая жестко скрепленная с плоскость, проходящая через ось вращения.
характеризует поворот всего твердого тела, которому принадлежат треугольник КLМ и ось вращения ί, и поэтому называется углом поворота. На такой же угол повернется любая жестко скрепленная с плоскость, проходящая через ось вращения.
В дальнейшем способ вращения вокруг осей, перпендикулярных плоскостям проекций, будет использован для решения разнообразных практических задач. Сейчас рассмотрим возможность его применения для перевода плоскости общего положении в положение проецирующей по отношению к плоскости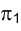 или
или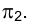
На основании изложенного в предыдущем параграфе ясно, что положение фронтально проецирующей плоскости в системе плоскостей проекций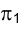
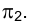 характеризуется тем, что все ее горизонтали
характеризуется тем, что все ее горизонтали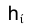 перпендикулярны фронтальной плоскости проекций
перпендикулярны фронтальной плоскости проекций 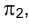 , а горизонтальные
, а горизонтальные 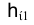 проекции этих горизонталей на эпюре Монжа совпадают с направлением линии связи. Аналогично положения горизонтально проецирующей плоскости характеризуются перпендикулярностью любой ее фронтали
проекции этих горизонталей на эпюре Монжа совпадают с направлением линии связи. Аналогично положения горизонтально проецирующей плоскости характеризуются перпендикулярностью любой ее фронтали 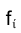 горизонтальной плоскости проекций
горизонтальной плоскости проекций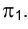 Фронтальная же проекция
Фронтальная же проекция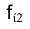 произвольной фронтали такой плоскости совпадает на эпюре Монжа с направлением проецирования точек
произвольной фронтали такой плоскости совпадает на эпюре Монжа с направлением проецирования точек
(рис. 2.14).
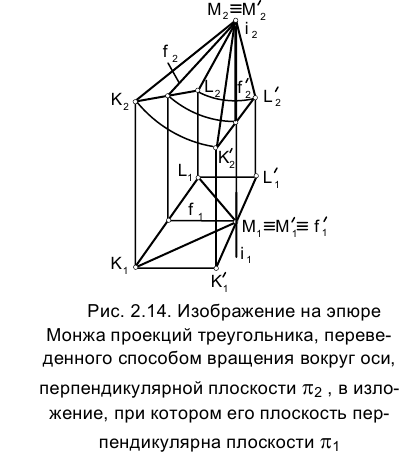
Приведенные рассуждения позволяют сформулировать следующие положения: для того чтобы с помощью способа вращения относительно осей, перпендикулярных плоскостям проекций, перевести плоскость общего положения 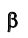 в горизонтально (фронтально) проецирующую, следует осуществить ее поворот относительно оси, перпендикулярной плоскости
в горизонтально (фронтально) проецирующую, следует осуществить ее поворот относительно оси, перпендикулярной плоскости 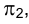 (
(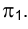 ) на угол
) на угол 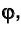 , обеспечивающий совпадение фронтальной (горизонтальной) проекции произвольной фронтали (горизонтали) плоскости
, обеспечивающий совпадение фронтальной (горизонтальной) проекции произвольной фронтали (горизонтали) плоскости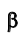 с линией связи.
с линией связи.
Сформулированное положение поясняется с помощью эпюры Монжа рис. 2.14. В обоих случаях плоскость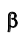 задана треугольником.
задана треугольником.
Вращение вокруг осей, параллельных плоскостям проекций В ряде случаев, когда требуется определить истинную величину угла между двумя прямыми, плоскостями, прямой и плоскостью, истинную форму несложной плоской фигуры, весьма эффективным оказывается способ вращения относительно осей, параллельных плоскостям проекций. Так, например, поворот плоскости общего положения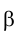 до положения, в котором она будет параллельной одной из плоскостей проекций
до положения, в котором она будет параллельной одной из плоскостей проекций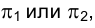 , можно осуществить либо вокруг ее произвольной горизонтали, либо вокруг произвольной фронтали.
, можно осуществить либо вокруг ее произвольной горизонтали, либо вокруг произвольной фронтали.
Необходимо, конечно, четко представить себе, что при вращении любая принадлежащая плоскости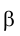 точка перемещается в плоскости, перпендикулярной оси вращения и той плоскости проекций, которой ось вращения параллельна (рис. 2.15).
точка перемещается в плоскости, перпендикулярной оси вращения и той плоскости проекций, которой ось вращения параллельна (рис. 2.15).
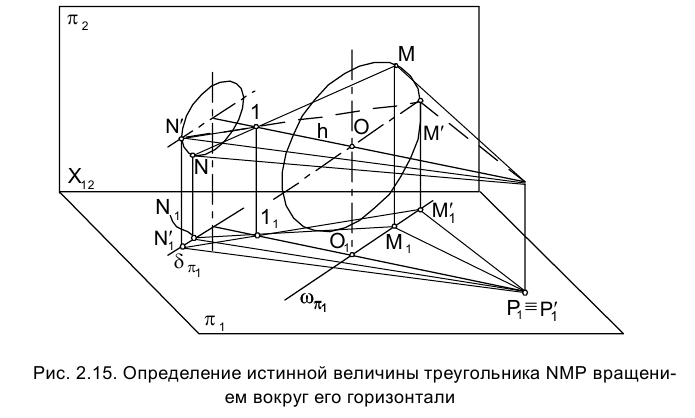
Иначе говоря, плоскость вращения любой принадлежащей плоскости 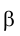 точки - проецирующая.
точки - проецирующая.
Отсюда следует вывод о том, что в процессе вращения произвольной точки F одна из ее проекций 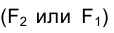 постоянно находится на пересечении (следе) плоскости ее вращение c той плоскостью проекций, которой ось вращения параллельна:
постоянно находится на пересечении (следе) плоскости ее вращение c той плоскостью проекций, которой ось вращения параллельна: 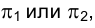 . Вторая же проекция вращающейся точки
. Вторая же проекция вращающейся точки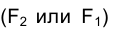 движется по некоторому эллипсу, и в ходе решения задачи ее положение, как правило, интереса не представляет.
движется по некоторому эллипсу, и в ходе решения задачи ее положение, как правило, интереса не представляет.
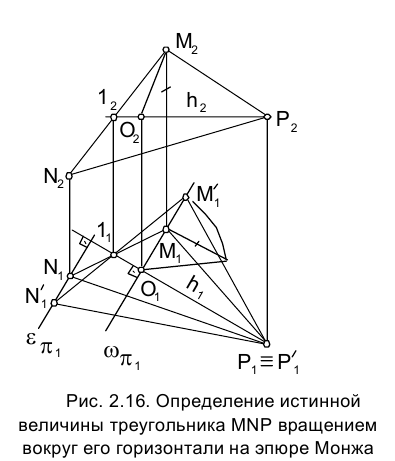
Проиллюстрируем существо изложенного способа на примере определения истинной величины треугольника МNР вращением его плоскости вокруг горизонтали h (рис. 2.16).
Пусть горизонталь h проходит через вершину Р треугольника и на эпюре Монжа задана отрезком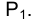 .
.
Истинная величина треугольника МNР определяется на эпюре на горизонтальной плоскости проекций p1 тогда, когда в процессе вращения плоскость треугольника станет параллельной плоскости 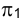 .
.
На рис. 2.16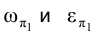 - следы на плоскости
- следы на плоскости 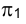 горизонтально проецирующих плоскостей, в которых по окружностям перемещаются вершины М и N треугольника. Точка Р лежит на оси h и в процессе вращения своего положения не имеет.
горизонтально проецирующих плоскостей, в которых по окружностям перемещаются вершины М и N треугольника. Точка Р лежит на оси h и в процессе вращения своего положения не имеет.
Проанализируем движение точки М при вращении плоскости треугольника МNР и построим ее новую горизонтальную проекцию 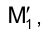 , соответствующую положению, когда плоскость
, соответствующую положению, когда плоскость  . Центром окружности, по которой в пространстве перемещается точка М, является точка пересечения горизонтально проецирующей плоскости
. Центром окружности, по которой в пространстве перемещается точка М, является точка пересечения горизонтально проецирующей плоскости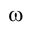 и оси вращения h. Радиус этой окружности измеряется длиной отрезка
и оси вращения h. Радиус этой окружности измеряется длиной отрезка 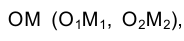 , истинная величина которого
, истинная величина которого 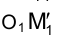 определится на следе горизонтально проецирующей плоскости
определится на следе горизонтально проецирующей плоскости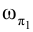 после завершения поворота плоскости треугольника МNР.
после завершения поворота плоскости треугольника МNР.
Истинная величина радиуса 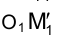 определится гипотенузой прямоугольного треугольника, в котором один из катетов - горизонтальная проекция радиуса
определится гипотенузой прямоугольного треугольника, в котором один из катетов - горизонтальная проекция радиуса 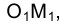 , а другой - разность удалений точки М и оси вращения от плоскости
, а другой - разность удалений точки М и оси вращения от плоскости 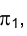 , измеренная отрезком
, измеренная отрезком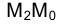 на плоскости
на плоскости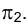 . Отрезок
. Отрезок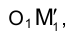 , определяющий положение вершины М истинной величины треугольника может быть отложен по направлению следа
, определяющий положение вершины М истинной величины треугольника может быть отложен по направлению следа 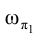 плоскости
плоскости 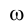 в любую сторону от точки
в любую сторону от точки 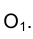 .
.
Положение вершины N треугольника МNР после завершения поворота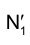 может быть найдено аналогично.
может быть найдено аналогично.
Можно однако определить положение вершины 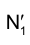 проще из тех соображений, что точка 1 как лежащая на оси вращения неподвижна и находится на стороне МN треугольника, причем точка N перемещается в плоскости
проще из тех соображений, что точка 1 как лежащая на оси вращения неподвижна и находится на стороне МN треугольника, причем точка N перемещается в плоскости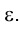 Поэтому, построив прямую
Поэтому, построив прямую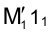 и продолжив ее до пересечения с
и продолжив ее до пересечения с 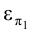 , найдем точку
, найдем точку 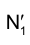 , а затем построим и истинную величину треугольника
, а затем построим и истинную величину треугольника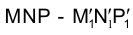 .
.
Применение способов преобразования чертежа к решению позиционных и метрических задач
В настоящем параграфе рассмотренные выше способы преобразования эпюра Монжа применяются для решения ряда типовых позиционных и метрических задач, представляющих наибольший практический интерес.
Задача 1. Способом замены плоскостей проекций определить расстояние между точками А и В (длину отрезка А В). Соединяя проекции точек А и В отрезками прямых линий, убеждаемся, что отрезок прямой АВ в пространстве определяет прямую общего положения и, следовательно, непосредственно на эпюре Монжа его длина не может быть измерена (рис. 2.17). Заменим фронтальную плоскость проекций 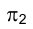 плоскостью
плоскостью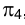 так же как и
так же как и 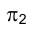 перпендикулярной горизонтальной плоскости проекций
перпендикулярной горизонтальной плоскости проекций 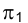 и одновременно параллельной отрезку АВ, так как перейдем от старой системы плоскостей проекции
и одновременно параллельной отрезку АВ, так как перейдем от старой системы плоскостей проекции 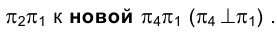 .
.
Поскольку на плоскости 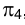 отрезок прямой АВ изобразится в истинную величину
отрезок прямой АВ изобразится в истинную величину 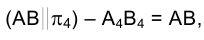 , то, следовательно, горизонтальная его проекция
, то, следовательно, горизонтальная его проекция 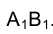 в системе плоскостей проекций
в системе плоскостей проекций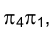 должна располагаться параллельно направлению оси проекций. Поэтому на эпюре Монжа новое направление проецирования точек в системе плоскостей проекций
должна располагаться параллельно направлению оси проекций. Поэтому на эпюре Монжа новое направление проецирования точек в системе плоскостей проекций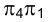 должно быть выбрано перпендикулярно отрезку
должно быть выбрано перпендикулярно отрезку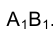 . Разности удалений точек А и В от горизонтальной плоскости проекций
. Разности удалений точек А и В от горизонтальной плоскости проекций 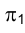 одинаковы в обеих системах плоскостей проекций: старой
одинаковы в обеих системах плоскостей проекций: старой 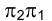 и новой
и новой 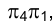 и на эпюре Монжа откладываются от так называемых линий отсчета - прямых, параллельных соответствующим осям проекций. На рис. 2.17 линия отсчета
и на эпюре Монжа откладываются от так называемых линий отсчета - прямых, параллельных соответствующим осям проекций. На рис. 2.17 линия отсчета 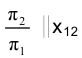 - оси проекций в новой системе Выполнив необходимые построения, получаем искомое расстояние между точками А и В в виде длины проекций отрезка АВ на плоскость p4. Характерным практическим примером определения расстояния между двумя точками является пример определения длины луча судового прожектора, освещающего спасательную шлюпку (рис. 2.18).
- оси проекций в новой системе Выполнив необходимые построения, получаем искомое расстояние между точками А и В в виде длины проекций отрезка АВ на плоскость p4. Характерным практическим примером определения расстояния между двумя точками является пример определения длины луча судового прожектора, освещающего спасательную шлюпку (рис. 2.18).
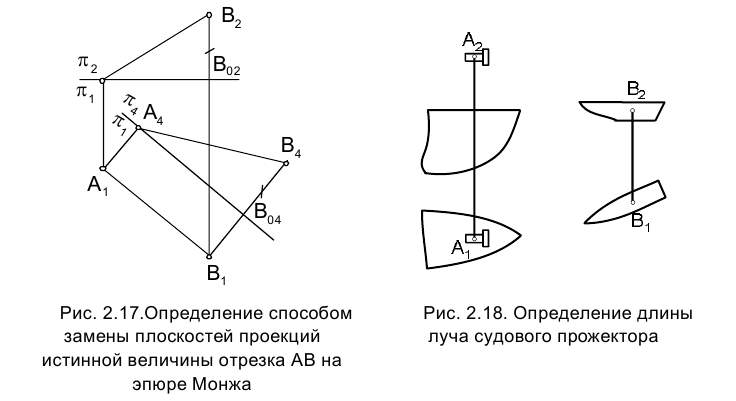
Задача 2. Способом замены плоскостей проекций определить расстояние от точки А до отрезка прямой СD.
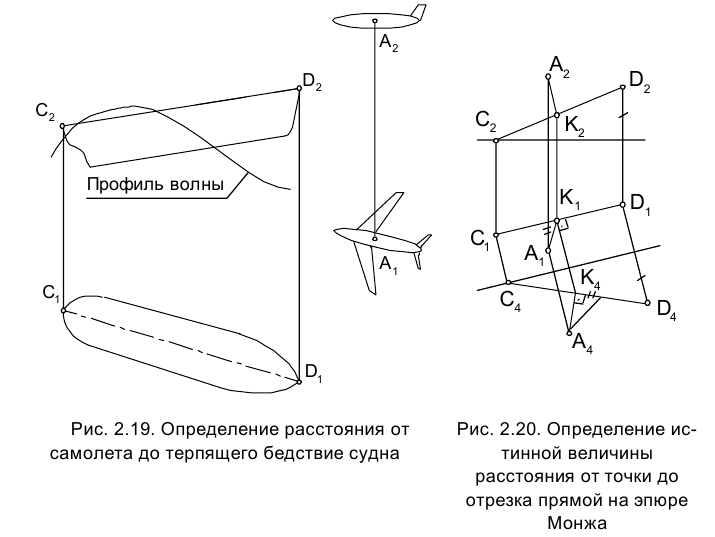
Сформулированное условие формализует целый ряд встречающихся на практике случаев, в частности определение расстояния от самолета до разыскиваемого им терпящего бедствие судна (рис.2.19). Самолет в этом случае моделируется точкой (ввиду его относительной малости по сравнению с судном), а судно - отрезком прямой.
В пространстве расстояние от точки А до отрезка СD определяется длиной АК перпендикуляра, опущенного из А на СD.
Для того чтобы на эпюре прямой угол изобразился в истинную величину, следует сначала отрезок СD перевести в положение, параллельное некоторой новой плоскости проекций, например 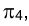 , т.е. перейти от старой системы
, т.е. перейти от старой системы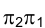 к новой
к новой 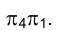 . На эпюре Монжа прямой угол, образованный в пространстве отрезком СD и перпендикуляром к нему АВ, сохранит свою величину и будет образован отрезками
. На эпюре Монжа прямой угол, образованный в пространстве отрезком СD и перпендикуляром к нему АВ, сохранит свою величину и будет образован отрезками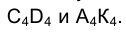 Определение затем истинной величины отрезка АК затруднений не вызывает (рис. 2.20).
Определение затем истинной величины отрезка АК затруднений не вызывает (рис. 2.20).
Задача 3. Способом замены плоскостей проекций определить расстояние от точки F до плоскости 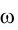 (рис. 2.21).
(рис. 2.21).
Если бы плоскость 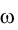 была перпендикулярна, например горизонтальной плоскости проекции
была перпендикулярна, например горизонтальной плоскости проекции 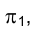 , то искомое расстояние можно было бы легко измерить непосредственно на
, то искомое расстояние можно было бы легко измерить непосредственно на 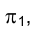 . Однако поскольку
. Однако поскольку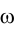 - плоскость общего положения на эпюре Монжа, нельзя непосредственно измерить расстояние до нее от точки F. Поэтому заменим плоскость
- плоскость общего положения на эпюре Монжа, нельзя непосредственно измерить расстояние до нее от точки F. Поэтому заменим плоскость 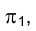 новой плоскостью проекций
новой плоскостью проекций 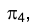 , перпендикулярной
, перпендикулярной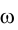 и
и 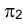 , т.е. переведем плоскость
, т.е. переведем плоскость 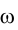 в положение проецирующей по отношению к плоскости
в положение проецирующей по отношению к плоскости 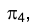 в новой
в новой 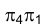 системе плоскостей проекций. Новая ось проекций
системе плоскостей проекций. Новая ось проекций 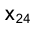 должна быть перпендикулярна линии пересечения плоскостей
должна быть перпендикулярна линии пересечения плоскостей 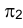 и w или, что то же самое, и фронтальной проекции произвольной фронтали, принадлежащей плоскости
и w или, что то же самое, и фронтальной проекции произвольной фронтали, принадлежащей плоскости 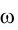
Проводим в треугольнике ВСD, задающем на эпюре Монжа плоскость 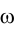 фронталь, например
фронталь, например 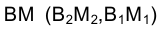 (рис. 2.22). Ее фронтальная проекция
(рис. 2.22). Ее фронтальная проекция 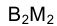 определит новое направление проецирования точек или линию связи новой системе плоскостей проекций
определит новое направление проецирования точек или линию связи новой системе плоскостей проекций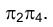 .
.
Имея в виду, что плоскость 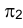 общая для обеих систем плоскостей проекций
общая для обеих систем плоскостей проекций 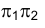 и
и 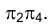 следовательно, разности удалений вершин треугольника BCD от плоскости
следовательно, разности удалений вершин треугольника BCD от плоскости 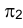 не меняются при переходе к новой системе плоскостей проекций
не меняются при переходе к новой системе плоскостей проекций 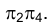 , строим точки
, строим точки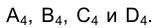 При этом плоскость треугольника ВСD на плоскости
При этом плоскость треугольника ВСD на плоскости 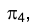 изобразится в виде отрезка прямой
изобразится в виде отрезка прямой 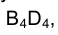 т.е. является проецирующей. Теперь остается измерить длину перпендикуляра
т.е. является проецирующей. Теперь остается измерить длину перпендикуляра 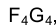 , опущенного из точки
, опущенного из точки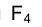 на отрезок
на отрезок 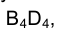 и определяющего расстояние от точки F до плоскости w.
и определяющего расстояние от точки F до плоскости w.
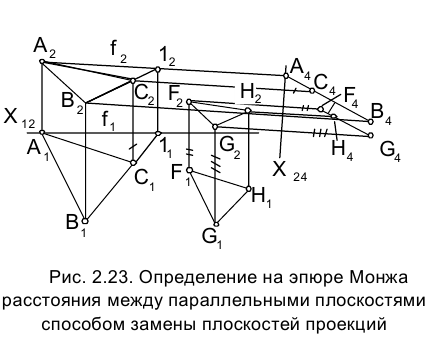
Задача 4. Способом замены плоскостей проекций определить расстояние между параллельными плоскостями 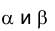 (рис. 2.23). На эпюре Монжа обе плоскости заданы проекциями треугольников
(рис. 2.23). На эпюре Монжа обе плоскости заданы проекциями треугольников 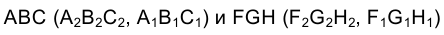 соответственно.
соответственно.
Используем идею решения задачи 3.
Введем плоскость, перпендикулярную a, 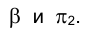 Искомое расстояние определится расстоянием между двумя параллельными прямыми, которые являются следами плоскостей
Искомое расстояние определится расстоянием между двумя параллельными прямыми, которые являются следами плоскостей 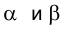 на плоскости
на плоскости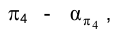
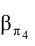 .
.
Задача 5. Способом замены плоскостей проекций определить расстояние между двумя скрещивающимися прямыми с и d, заданными отрезками СF и МN соответственно.
В подобной постановке отыскание решения поставленной задачи на практике соответствует отысканию расстояния между линиями
высоковольтных передач (рис. 2.24).
Вспомним, что расстояние между скрещивающимися прямыми определяется длиной перпендикуляра, опущенного из любой точки одной из скрещивающихся прямых на плоскость, проведенную через другую прямую параллельно первой.
Через произвольную точку 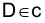 проводим прямую b (FЕ)D d, тогда плоскость
проводим прямую b (FЕ)D d, тогда плоскость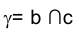 параллельна d. Выберем на прямой d удобную для нас точку и определим расстояние до плоскости
параллельна d. Выберем на прямой d удобную для нас точку и определим расстояние до плоскости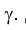 Для этого переведем предварительно плоскость
Для этого переведем предварительно плоскость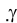 в проецирующую по отношению к новой плоскости проекций
в проецирующую по отношению к новой плоскости проекций 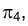 , заменяющей плоскость
, заменяющей плоскость 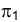 .
.
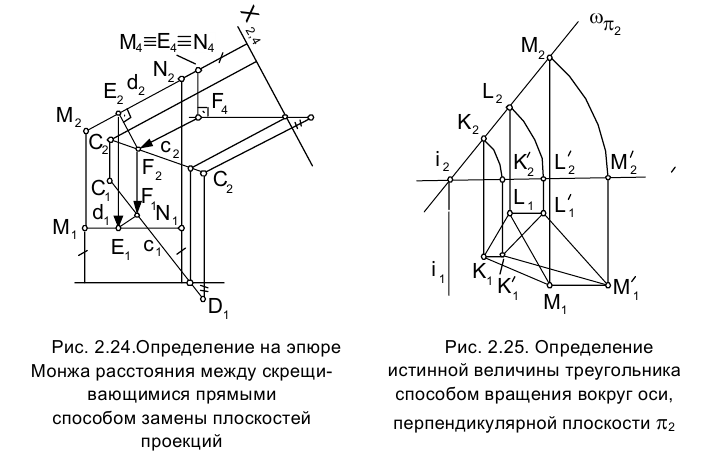
Задача 6. Способом вращения вокруг оси ί перпендикулярной плоскости проекций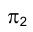 определить истинную форму треугольника
определить истинную форму треугольника 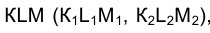 лежащего во фронтально проецирующей плоскости
лежащего во фронтально проецирующей плоскости 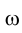 (рис. 2.25). На эпюре Монжа истинная форма треугольника КLМ определится на горизонтальной плоскости проекций
(рис. 2.25). На эпюре Монжа истинная форма треугольника КLМ определится на горизонтальной плоскости проекций 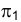 тогда, когда плоскость
тогда, когда плоскость 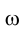 будет ей параллельна. Такому положению плоскости
будет ей параллельна. Такому положению плоскости 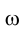 будет соответствовать параллельность ее следа
будет соответствовать параллельность ее следа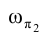 направлению оси проекций
направлению оси проекций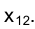 .
.
Таким образом, в процессе поворота плоскости 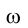 относительно оси
относительно оси 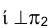 фронтальные проекции
фронтальные проекции 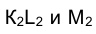 вершин треугольника КLМ будут (см. раздел 1.7) перемещаться по дугам концентрических окружностей с центром в точке
вершин треугольника КLМ будут (см. раздел 1.7) перемещаться по дугам концентрических окружностей с центром в точке 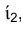 , а горизонтальные их проекции
, а горизонтальные их проекции 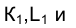
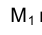 по прямым линиям, параллельным направлению оси проекций
по прямым линиям, параллельным направлению оси проекций 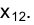 .
.
Новые горизонтальные проекции вершин треугольника 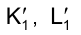 и
и 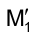 найдутся на пересечении траектории движения точек
найдутся на пересечении траектории движения точек 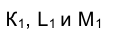 с направлениями проецирования, проходящими через новые фронтальные проекции вершин треугольника
с направлениями проецирования, проходящими через новые фронтальные проекции вершин треугольника 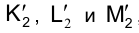 , определяемые новым - параллельным направлению оси проекций
, определяемые новым - параллельным направлению оси проекций 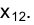 положением следа плоскости
положением следа плоскости 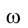 на плоскости
на плоскости 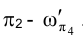
Следует отметить, что приведенный выше алгоритм определения истинной формы плоской фигуры, расположенной в проецирующей плоскости вместе с рассмотренным в разделе 1.7 алгоритмом перевода плоскости общего положения в проецирующую, определяет решение задачи о нахождении истинной формы плоской фигуры, лежащей в плоскости общего положения.
Задача 7. Способом вращения относительно оси h, параллельной плоскости проекций 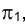 , определить истинную величину угла при точке В между двумя пересекающимися прямыми p и n (рис. 2.26).
, определить истинную величину угла при точке В между двумя пересекающимися прямыми p и n (рис. 2.26).
Построим горизонталь h плоскости пересекающихся прямых и обозначим точки ее пересечения с прямыми р и n - 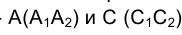 соответственно. Истинная величина угла при точке В определится на горизонтальной плоскости проекций
соответственно. Истинная величина угла при точке В определится на горизонтальной плоскости проекций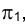 , тогда, когда его плоскость в результате поворота станет параллельна
, тогда, когда его плоскость в результате поворота станет параллельна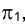 . Точки А и С как лежащие на оси вращения перемещаться не будут, и, следовательно, необходимо проанализировать лишь движение точки В.
. Точки А и С как лежащие на оси вращения перемещаться не будут, и, следовательно, необходимо проанализировать лишь движение точки В.
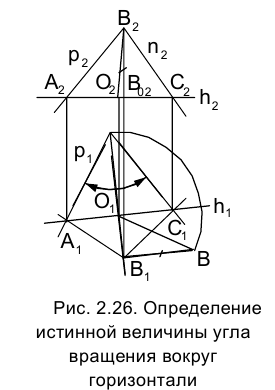
В пространстве точка В (см. раздел 1.7) перемещается в горизонтально проецирующей плоскости, перпендикулярной к оси вращения, - h горизонтали h (АС). След плоскости вращения: точки В на плоскости 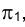 , проходит через горизонтальную проекцию точки
, проходит через горизонтальную проекцию точки 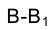 перпендикулярно к h (
перпендикулярно к h (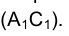 Центр окружности О, по которой в пространстве движется точка В, проецируется на плоскость
Центр окружности О, по которой в пространстве движется точка В, проецируется на плоскость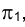 в точку О1, и, следовательно, отрезок
в точку О1, и, следовательно, отрезок 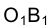 - горизонтальная проекция радиуса этой окружности. Истинная величина ее радиуса изобразится на горизонтальной плоскости проекций
- горизонтальная проекция радиуса этой окружности. Истинная величина ее радиуса изобразится на горизонтальной плоскости проекций 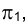 тогда, когда плоскость прямых р и п будет ей параллельна.
тогда, когда плоскость прямых р и п будет ей параллельна.
Определяя истинную величину радиуса как гипотенузу прямоугольного треугольника 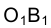 В, где
В, где 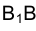 =
= 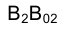 разность удалений точки В и оси вращения h от горизонтальной плоскости проекций
разность удалений точки В и оси вращения h от горизонтальной плоскости проекций 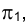 , и откладывая ее на направлении следа плоскости вращения точки В, находим новую горизонтальную проекцию точки
, и откладывая ее на направлении следа плоскости вращения точки В, находим новую горизонтальную проекцию точки 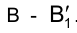 . Соединяя точку
. Соединяя точку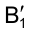 с точками А и С, находим искомый угол - угол при точке В.
с точками А и С, находим искомый угол - угол при точке В.
Преобразование изображений. Четыре основные задачи начертательной геометрии
Для упрощения решения метрических, а также некоторых позиционных задач, могут применяться методы, позволяющие переходить от задания фигур общих положений к частным. Эти методы основываются на двух принципах:
- замещение системы плоскостей проекций на новую систему плоскостей, в которой неподвижный геометрический объект занимает какое-либо частное положение (способ замены плоскостей проекций);
- перемещение геометрического объекта в пространстве таким образом, чтобы он занял какое-либо частное положение в неподвижной системе плоскостей (способ вращения).
В зависимости от положение оси в пространстве, вокруг которой вращается геометрический объект, различают следующие виды способа вращения:
- вращение вокруг линии уровня;
- вращение вокруг проецирующей прямой;
- плоско-параллельное перемещение.
Эти способы преобразования включают в себя четыре основные задачи начертательной геометрии:
- Преобразование комплексного чертежа таким образом, чтобы прямая общего положения стала линией уровня.
- Преобразование комплексного чертежа таким образом, чтобы линия уровня стала проецирующей прямой.
- Преобразование комплексного чертежа таким образом, чтобы плоскость общего положения стала проецирующей плоскостью уровня.
- Преобразование комплексного чертежа таким образом, чтобы проецирующая плоскость стала плоскостью уровня.
Преобразование комплексного чертежа
Способ замены плоскостей проекций:
Этот способ состоит в том, что заданная фигура неподвижна, а одна из основных плоскостей V или H заменяется новой дополнительной плоскостью 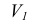 или
или 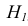 , расположенной параллельно или перпендикулярно заданной геометрической фигуре. Точка A задана в системе V/H (рис. 4.1). Плоскость V заменена новой плоскостью
, расположенной параллельно или перпендикулярно заданной геометрической фигуре. Точка A задана в системе V/H (рис. 4.1). Плоскость V заменена новой плоскостью 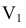 перепендикулярной H.
перепендикулярной H.
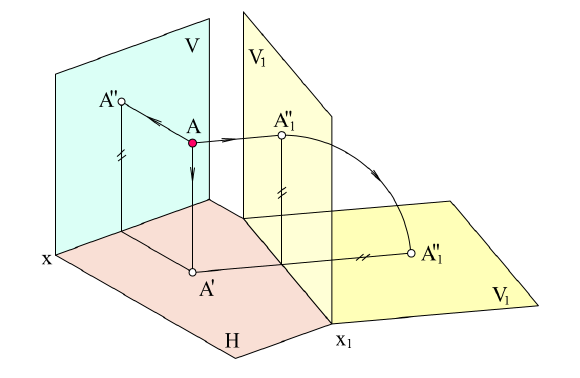
Рисунок 4.1 – Замена фронтальной плоскости проекций
Плоскость H является общей в системе 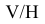 и
и 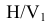 , то координата
, то координата 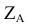 остается неизменной. Следовательно, расстояние от новой фронтальной проекции до новой оси
остается неизменной. Следовательно, расстояние от новой фронтальной проекции до новой оси 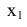 равно расстоянию от заменяемой проекции до оси X.
равно расстоянию от заменяемой проекции до оси X.
Для получения плоского чертежа точки 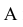 плоскость
плоскость 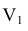 вращают вокруг оси
вращают вокруг оси 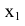 до совмещения с плоскостью H.
до совмещения с плоскостью H.
Новая фронтальная проекция 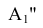 точки
точки 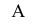 окажется на общем перпендикуляре к новой оси x1 с оставшейся без изменения ее проекции
окажется на общем перпендикуляре к новой оси x1 с оставшейся без изменения ее проекции 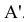 .
.
Задача. Преобразовать чертеж так, чтобы прямая общего положения оказалась параллельной одной из плоскостей проекций.
Новую проекцию прямой, отвечающую поставленной задачи, можно построить (рис. 4.2) на новой плоскости проекций 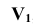 , расположив ее параллельно самой прямой и перпендикулярно плоскости
, расположив ее параллельно самой прямой и перпендикулярно плоскости 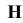 . От системы плоскостей
. От системы плоскостей 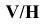 с осью проекций
с осью проекций 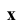 следует перейти к системе
следует перейти к системе 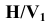 с новой осью
с новой осью 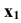 .
.
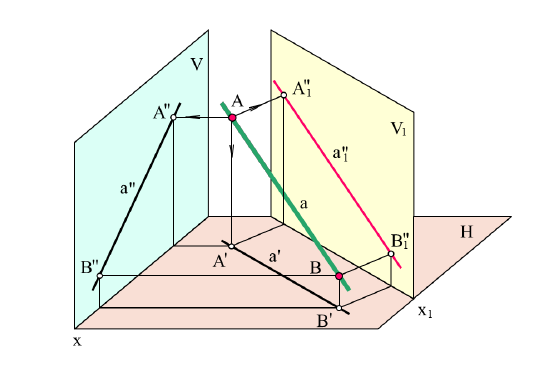
Рисунок 4.2 – Определение натуральной величины отрезка AB заменой фронтальной плоскости проекций
На плоском чертеже (рис. 4.3 а) новая ось 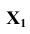 проведена параллельно a', новые линии связи
проведена параллельно a', новые линии связи 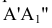 и
и 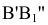 проведены перпендикулярно оси
проведены перпендикулярно оси 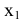 . Новые фронтальные проекции
. Новые фронтальные проекции 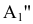 и
и 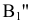 точек A и B получают, измерив от оси x на поле V координаты высот
точек A и B получают, измерив от оси x на поле V координаты высот 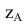 и
и 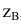 , отложив их от оси
, отложив их от оси 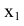 на новое поле
на новое поле 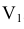 .
.
Новая проекция 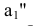 дает натуральную величину отрезка AB и угол a наклона его к плоскости H.
дает натуральную величину отрезка AB и угол a наклона его к плоскости H.
Угол наклона прямой a к плоскости V можно определить, построив изображение прямой на другой дополнительной плоскости 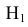 V, где
V, где 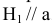 .
.
На плоском чертеже (рис. 4.3 б) новая ось 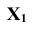 проведена параллельно a', новые линии связи
проведена параллельно a', новые линии связи 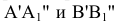 проведены перпендикулярно оси
проведены перпендикулярно оси 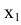 . Новые фронтальные проекции
. Новые фронтальные проекции 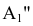 и
и 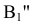 точек A и B получают, измерив от оси X на поле V координаты высот
точек A и B получают, измерив от оси X на поле V координаты высот 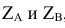 , отложив их от оси
, отложив их от оси 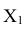 на новое поле
на новое поле 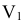 .
.
Новая проекция 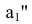 дает натуральную величину отрезка AB и угол α наклона его к плоскости H.
дает натуральную величину отрезка AB и угол α наклона его к плоскости H.
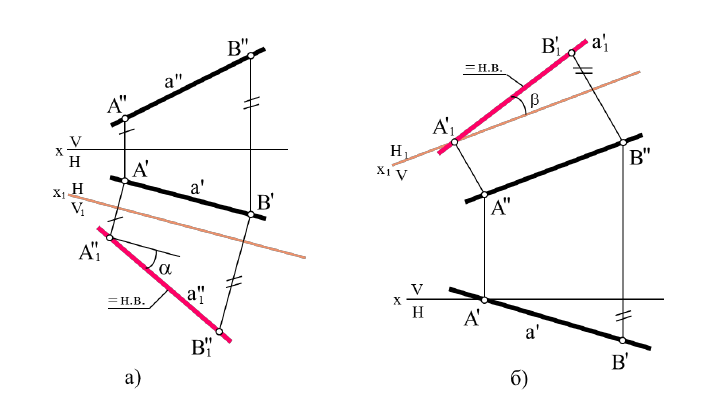 Рисунок 4.3 – Определение натуральной величины отрезка AB способом замены плоскости проекций ( а- фронтальной, б - горизонтальной)
Рисунок 4.3 – Определение натуральной величины отрезка AB способом замены плоскости проекций ( а- фронтальной, б - горизонтальной)
Угол наклона прямой a к плоскости V можно определить, построив изображение прямой на другой дополнительной плоскости 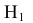 V, где H1//
V, где H1// 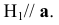
Способ плоскопараллельного перемещения
При плоскопараллельном перемещении заданная фигура движется в пространстве так, что все её точки перемещаются в плоскостях, параллельных друг другу и (как правило) параллельно одной из плоскостей проекций. Сами траектории точек фигуры произвольны.
Способ плоскопараллельного перемещения (переноса) имеет справедливым утверждение, которое может быть выражено в виде следующей теоремы.
При параллельном переносе геометрической фигуры относительно плоскости проекции, проекция фигуры на эту плоскость хотя и меняет свое положение, но остается конгруентной проекции фигуры в ее исходном положении.
Пользуясь отмеченными свойствами, не составляет труда построить новые проекции геометрической фигуры (по заданным ее ортогональным проекциям), которые соответствуют частным положениям проецируемой фигуры по отношению к плоскости проекции.
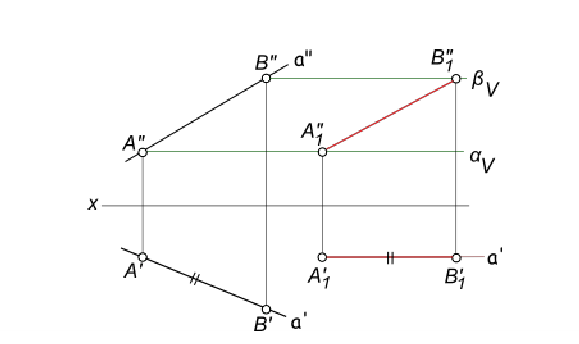
Рисунок 4.4 – Определение натуральной величины отрезка AB способом плоскопараллельного перемещения
[AB]- отрезок прямой общего положения перевести в положение параллельное V. Выполняем перемещение отрезка [A`B`] на горизонтальной плоскости проекции в положение параллельное оси x 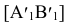 (рис.4.4). При таком перемещении новая горизонтальная проекция конгруентна исходной
(рис.4.4). При таком перемещении новая горизонтальная проекция конгруентна исходной 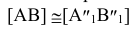 на основании теоремы.
на основании теоремы.
Фронтальные проекции точек отрезка [A"B"] будут перемещаться в новое положение 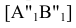 в плоскостях α и β параллельных горизонтальной плоскости проекции - по следам
в плоскостях α и β параллельных горизонтальной плоскости проекции - по следам 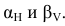 .
.
Для перевода отрезка прямой общего положения в положение параллельное V требуется одно перемещение отрезка параллельно плоскости проекции H.
Для перевода отрезка прямой из общего положения в проецирующее (рис.4.5), необходимо последовательно выполнить два перемещения параллельно плоскостям проекции и перпендикулярно плоскости проекции.
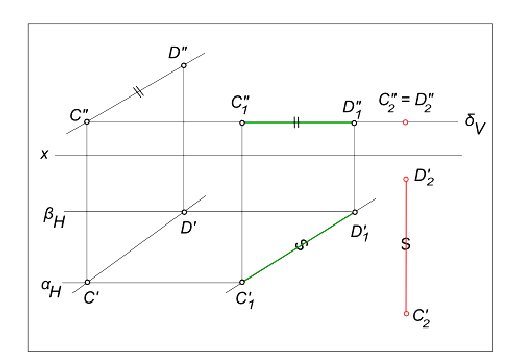
Рисунок 4.5 – Поэтапный перевода отрезка СD параллельно плоскости проекции H и перпендикулярно плоскости проекции V
Зная характер геометрических построений, которые необходимо выполнить для перемещения отрезка из общего положения в проецирующее, можно легко перевести плоскость треугольника АВС, произвольно расположенную в пространстве, в частное положение (рис.4.6) (перпендикулярное или параллельное плоскости проекции) и определить его натуральную величину.
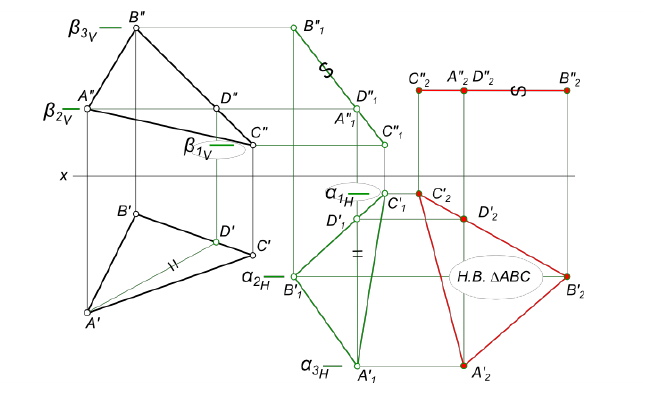
Рисунок 4.6 – Определение натуральной величины ∆АВС
Способ вращения вокруг проецирующей прямой
К частным случаям метода плоскопараллельного перемещения относятся метод вращения вокруг проецирующих прямых, а так же метод вращения вокруг прямых уровня.
Сущность этого способа заключается в том, что система плоскостей проекций V/H остается неподвижной, а положение геометрических элементов меняется путем вращения вокруг одной или двух выбранных осей до нужного положения в данной системе. Этим способом решаются задачи на определение: натуральной величины отрезков и углов их наклона к плоскостям проекций V, H или W; для проведения прямой и плоскости под заданными углами; для совмещения оригиналов.
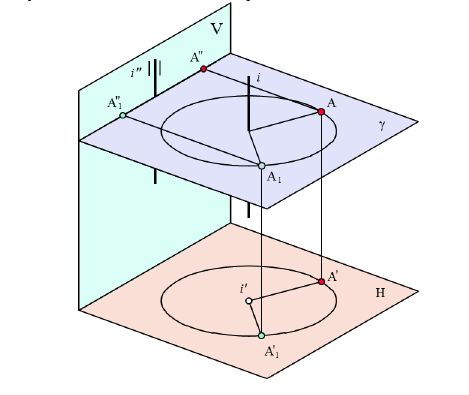
Рисунок 4.7 – Вращение точки вокруг оси
Точка A, вращаясь вокруг горизонтально проецирующей оси i, опишет окружность, плоскость которой γ перпендикулярна i и параллельна H. На плоскость H эта окружность проецируется без искажения, а на плоскость V -в виде отрезка прямой, параллельной оси x. Центр окружности расположен в точке пересечения оси вращения i с плоскостью γ, а величина радиуса определится как расстояние от точки A до оси i.
Задача. Преобразовать чертеж так, чтобы прямая общего положения оказалась параллельной одной из плоскостей проекций. Если прямая параллельна плоскости проекций V или H, то одна из ее проекций должна быть параллельна оси x или перпендикулярна линиям связи. На рисунке 4.8 за ось вращения i взята горизонтально проецирующая прямая, проходящая через точку A. Точка A при вращении прямой a остается неподвижной, а другая ее точка B вращается в горизонтальной плоскости уровня γ. Ее горизонтальная проекция B' опишет дугу окружности, а угол поворота точки B определяется условием перпендикулярности новой проекции a'1 прямой a к линиям связи.
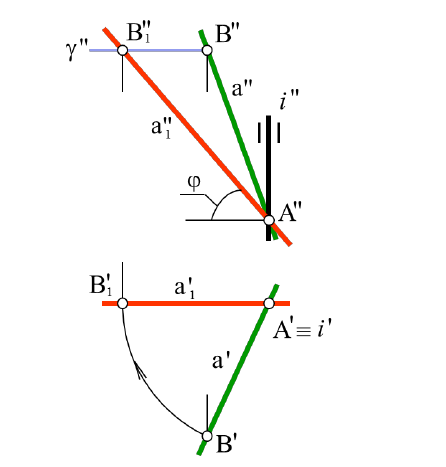
Рисунок 4.8 – Определение натуральной величины отрезка AB способом вращения вокруг оси
В результате такого поворота на плоскости V в натуральную величину проецируется отрезок AB и угол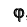 , который прямая a составляет с плоскостью H. Итак, одним поворотом вокруг проецирующей оси прямую общего положения можно расположить параллельно одной из плоскостей проекций.
, который прямая a составляет с плоскостью H. Итак, одним поворотом вокруг проецирующей оси прямую общего положения можно расположить параллельно одной из плоскостей проекций.
Методы преобразования чертежа. Метод замены плоскостей проекций
При решении задач на определение истинной величины отрезка прямой линии, плоской фигуры или наклона их к плоскостям проекций, а также на определение расстояний между точкой и прямой или плоской фигурой было замечено, что если эти прямые или плоские фигуры «удобно» расположены относительно плоскостей проекций, т.е. занимают частное положение, то задачи имеют простые решения. Сравним решение двух задач. Пусть требуется определить истинную величину отрезков 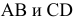 (рис. 6.1). В первом случае отрезок
(рис. 6.1). В первом случае отрезок 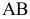 занимает общее положение (см. рис. 6.1, а), во втором отрезок
занимает общее положение (см. рис. 6.1, а), во втором отрезок 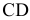 занимает частное положение (см. рис. 6.1, б).
занимает частное положение (см. рис. 6.1, б).
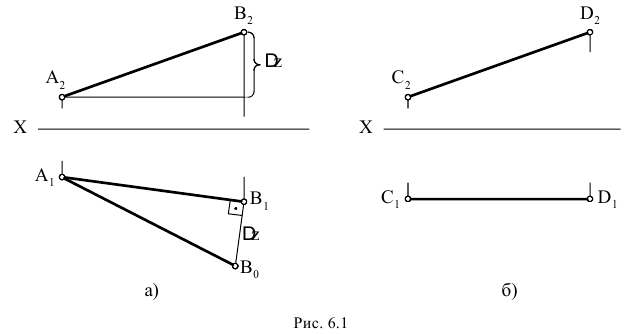
Истинная величина отрезка 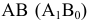 определена при помощи прямоугольного треугольника. Что же касается отрезка
определена при помощи прямоугольного треугольника. Что же касается отрезка 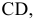 то истинная величина его равняется
то истинная величина его равняется 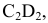 т.к. отрезок расположен параллельно плоскости проекций
т.к. отрезок расположен параллельно плоскости проекций 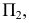 т.е. решение задачи вытекает из самого чертежа.
т.е. решение задачи вытекает из самого чертежа.
Если заданные геометрические элементы расположены наклонно ко всем плоскостям проекций, то, применяя метод замены плоскостей проекций, т.е. дополняя основную систему плоскостей проекций 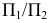 одной или несколькими новыми плоскостями проекций, переходим к такому положению, когда геометрические элементы в новой системе плоскостей проекций, например,
одной или несколькими новыми плоскостями проекций, переходим к такому положению, когда геометрические элементы в новой системе плоскостей проекций, например, 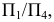 занимают частное положение.
занимают частное положение.
Метод замены плоскостей проекций заключается в том, что одна из основных плоскостей проекций, 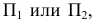 заменяется новой плоскостью проекций
заменяется новой плоскостью проекций 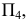 перпендикулярной к незаменяемой плоскости проекций. Например, если заменяется плоскость проекций
перпендикулярной к незаменяемой плоскости проекций. Например, если заменяется плоскость проекций 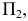 то новая плоскость проекций
то новая плоскость проекций 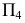 должна быть расположена перпендикулярно
должна быть расположена перпендикулярно 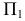 и параллельно, например, проецируемому отрезку. При данном методе положение в пространстве отрезков прямых или плоских фигур не изменяется.
и параллельно, например, проецируемому отрезку. При данном методе положение в пространстве отрезков прямых или плоских фигур не изменяется.
Рассмотрим построение проекции точки 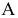 в новой системе плоскостей проекций
в новой системе плоскостей проекций 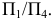 Для этого основную систему плоскостей проекций
Для этого основную систему плоскостей проекций 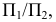 дополняем новый плоскостью проекций
дополняем новый плоскостью проекций 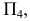 расположенной перпендикулярно
расположенной перпендикулярно 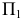 в произвольном месте (рис. 6.2, а). Линия пересечения этих плоскостей образует новую ось проекций
в произвольном месте (рис. 6.2, а). Линия пересечения этих плоскостей образует новую ось проекций 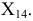
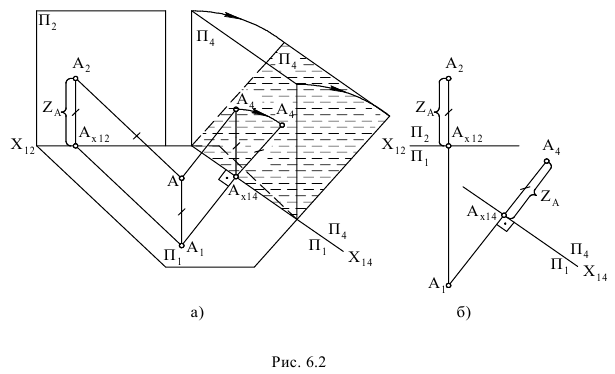
Положение точки 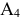 в новой системе плоскостей проекций
в новой системе плоскостей проекций 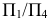 определяем так же, как и в системе
определяем так же, как и в системе 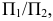 т.е. из точки
т.е. из точки 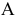 проводим перпендикуляр до пересечения с плоскостью проекций
проводим перпендикуляр до пересечения с плоскостью проекций 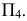 Затем плоскость
Затем плоскость 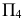 совмещаем с плоскостью проекций
совмещаем с плоскостью проекций 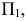 как совмещали плоскость проекций
как совмещали плоскость проекций 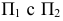 при нахождении проекций точек, расположенных в первой четверти. Проекции
при нахождении проекций точек, расположенных в первой четверти. Проекции 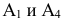 точки будут лежать на одном перпендикуляре к оси
точки будут лежать на одном перпендикуляре к оси 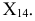
Чтобы построить чертеж точки 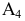 в новой системе плоскостей проекций (см. рис. 6.2, б), проводим из точки
в новой системе плоскостей проекций (см. рис. 6.2, б), проводим из точки 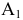 перпендикуляр к новой оси проекций, а затем на продолжении этого перпендикуляра от оси
перпендикуляр к новой оси проекций, а затем на продолжении этого перпендикуляра от оси 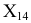 откладываем расстояние, равное
откладываем расстояние, равное 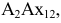 взятое с фронтальной плоскости проекций
взятое с фронтальной плоскости проекций 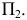
При необходимости замены плоскости проекций 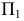 новую плоскость проекций
новую плоскость проекций 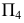 располагаем перпендикулярно
располагаем перпендикулярно 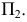 Остальное решение аналогично предыдущему.
Остальное решение аналогично предыдущему.
Определим натуральную величину отрезка 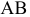 и угол наклона его к горизонтальной плоскости проекций методом замены плоскостей проекций (рис. 6.3).
и угол наклона его к горизонтальной плоскости проекций методом замены плоскостей проекций (рис. 6.3).
Учитывая, что одновременно нужно определить величину отрезка 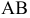 и угол наклона его к
и угол наклона его к 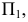 необходимо, чтобы новая дополнительная плоскость проекций
необходимо, чтобы новая дополнительная плоскость проекций 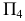 была расположена параллельно отрезку
была расположена параллельно отрезку 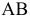 и перпендикулярно плоскости проекций
и перпендикулярно плоскости проекций 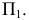 Таким образом, на горизонтальной плоскости проекций
Таким образом, на горизонтальной плоскости проекций 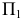 проводим новую ось проекций
проводим новую ось проекций 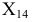 параллельно
параллельно 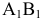 на произвольном расстоянии от
на произвольном расстоянии от 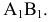 Отрезок
Отрезок 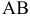 спроецируется на новую плоскость проекций
спроецируется на новую плоскость проекций 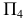 в натуральную величину. Построение проекции
в натуральную величину. Построение проекции 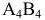 показано на чертеже. Из точек
показано на чертеже. Из точек 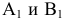 проведены перпендикуляры к оси проекции
проведены перпендикуляры к оси проекции 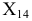 и от этой оси на продолжении перпендикуляров отложены величины расстояний, взятые с фронтальной плоскости проекций (показано засечками).
и от этой оси на продолжении перпендикуляров отложены величины расстояний, взятые с фронтальной плоскости проекций (показано засечками).
Угол 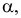 заключенный между найденной проекцией
заключенный между найденной проекцией 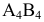 и осью проекций
и осью проекций 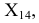 равняется углу наклона отрезка к горизонтальной плоскости проекций.
равняется углу наклона отрезка к горизонтальной плоскости проекций.
Для того чтобы определить угол наклона отрезка 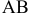 к фронтальной плоскости проекций, необходимо новую плоскость проекций расположить параллельно отрезку и перпендикулярно фронтальной плоскости проекций, т.е. новая ось на эпюре должна пройти параллелью
к фронтальной плоскости проекций, необходимо новую плоскость проекций расположить параллельно отрезку и перпендикулярно фронтальной плоскости проекций, т.е. новая ось на эпюре должна пройти параллелью 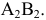 Дальнейшее решение аналогично предыдущему.
Дальнейшее решение аналогично предыдущему.
На рис. 6.4 приведен пример преобразования отрезка 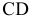 в проецирующее положение в новой системе плоскостей проекций
в проецирующее положение в новой системе плоскостей проекций 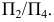 Так как отрезок
Так как отрезок 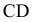 занимает частное положение, т.е. расположен параллельно плоскости проекций
занимает частное положение, т.е. расположен параллельно плоскости проекций 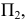 то при расположении дополнительной плоскости проекций
то при расположении дополнительной плоскости проекций 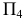 (ось
(ось 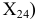 перпендикулярно плоскости проекций
перпендикулярно плоскости проекций 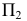 и отрезку
и отрезку 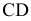 последний спроецируется в точку, т.е.
последний спроецируется в точку, т.е. 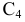 совпадет с
совпадет с 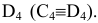 Это видно из чертежа, т.к. горизонтальные проекции точек
Это видно из чертежа, т.к. горизонтальные проекции точек 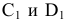 отстоят на одинаковом расстоянии от оси
отстоят на одинаковом расстоянии от оси 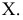
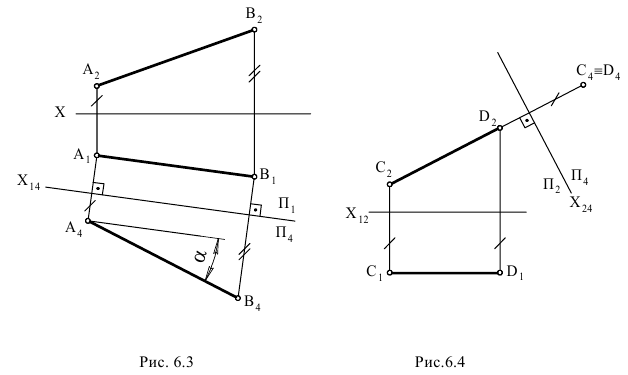
Чтобы преобразовать плоскость общего положения 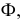 заданную следами (рис. 6.5), в проецирующее положение, необходимо дополнительную плоскость
заданную следами (рис. 6.5), в проецирующее положение, необходимо дополнительную плоскость 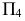 расположить перпендикулярно данной плоскости и перпендикулярно одной из плоскостей проекций
расположить перпендикулярно данной плоскости и перпендикулярно одной из плоскостей проекций 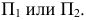 Для сравнения на рис. 6.6 показаны горизонтально-проецирующая плоскость (см. рис. 6.6, а) и фронтально-проецирующая
Для сравнения на рис. 6.6 показаны горизонтально-проецирующая плоскость (см. рис. 6.6, а) и фронтально-проецирующая 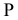 (см. рис. 6.6, б), у которых один из следов перпендикулярен оси
(см. рис. 6.6, б), у которых один из следов перпендикулярен оси 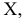 а это значит, что он перпендикулярен и одной из плоскостей проекций.
а это значит, что он перпендикулярен и одной из плоскостей проекций.
Для решения задачи необходимо плоскость 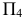 расположить перпендикулярно горизонтальному следу
расположить перпендикулярно горизонтальному следу 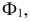 который является линией пересечения плоскости
который является линией пересечения плоскости 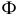 и плоскости проекций
и плоскости проекций 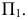 Это значит, что ось
Это значит, что ось 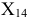 должна быть проведена перпендикулярно следу
должна быть проведена перпендикулярно следу 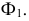 Следовательно, плоскость
Следовательно, плоскость 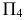 одновременно займет положение, перпендикулярное
одновременно займет положение, перпендикулярное 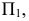 что является необходимым условием при замене плоскостей проекций. Чтобы построить след
что является необходимым условием при замене плоскостей проекций. Чтобы построить след 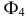 в новой системе плоскостей проекций
в новой системе плоскостей проекций 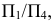 возьмем на следе
возьмем на следе 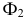 фронтальную проекцию точки
фронтальную проекцию точки 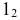 и найдем точку
и найдем точку 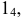 принадлежащую фронтальному следу в новой системе плоскостей проекций. Проведя прямую линию через точку
принадлежащую фронтальному следу в новой системе плоскостей проекций. Проведя прямую линию через точку 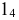 и точку пересечения следа
и точку пересечения следа 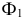 с осью проекций
с осью проекций 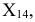 получим фронтальный след
получим фронтальный след 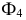 в новой системе плоскостей проекций. Плоскость же, заданная следами
в новой системе плоскостей проекций. Плоскость же, заданная следами 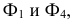 является фронтально-проецирую-щей в новой системе плоскостей проекций.
является фронтально-проецирую-щей в новой системе плоскостей проекций.
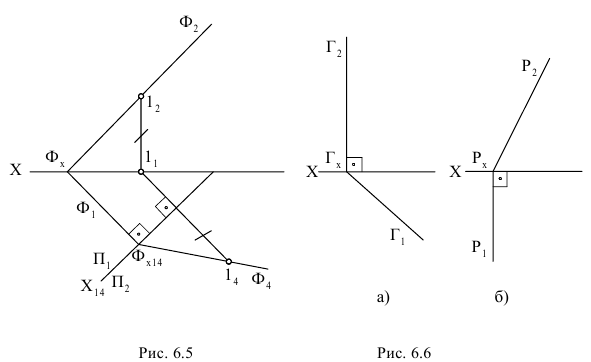
Задача решается аналогично при замене горизонтальной плоскости проекций.
Рассмотрим задачу, для решения которой замена одной плоскости проекций дополнительной плоскостью проекций является недостаточной. Пусть требуется преобразовать систему плоскостей проекций так, чтобы отрезок 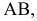 занимающий в основной системе плоскостей проекций
занимающий в основной системе плоскостей проекций 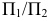 общее положение, в новой системе был бы перпендикулярен одной из плоскостей проекций, т.е. спроецировался бы в точку.
общее положение, в новой системе был бы перпендикулярен одной из плоскостей проекций, т.е. спроецировался бы в точку.
Новую плоскость проекций выбрать так, чтобы она была перпендикулярна отрезку 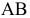 и одной из плоскостей проекций, невозможно, т.к. отрезок занимает общее положение. Поэтому необходимо вначале применить промежуточную плоскость проекций
и одной из плоскостей проекций, невозможно, т.к. отрезок занимает общее положение. Поэтому необходимо вначале применить промежуточную плоскость проекций 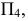 которую нужно расположить параллельно отрезку
которую нужно расположить параллельно отрезку 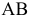 и перпендикулярно
и перпендикулярно 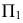 (рис. 6.7).
(рис. 6.7).
Для этого проводим новую ось проекций параллельно отрезку 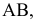 т.е.
т.е. 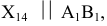 и строим новую фронтальную проекцию отрезка
и строим новую фронтальную проекцию отрезка 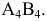 Вторую дополнительную плоскость проекций
Вторую дополнительную плоскость проекций 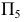 в системе
в системе 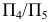 располагаем перпендикулярно промежуточной плоскости проекций
располагаем перпендикулярно промежуточной плоскости проекций 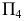 и отрезку
и отрезку 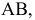 т.е. ось проекций
т.е. ось проекций 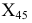 проводим перпендикулярно проекции отрезка
проводим перпендикулярно проекции отрезка 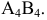 Точки
Точки 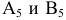 совпадают, т.к. отрезок
совпадают, т.к. отрезок 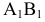 расположен на одинаковом расстоянии от оси
расположен на одинаковом расстоянии от оси 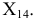
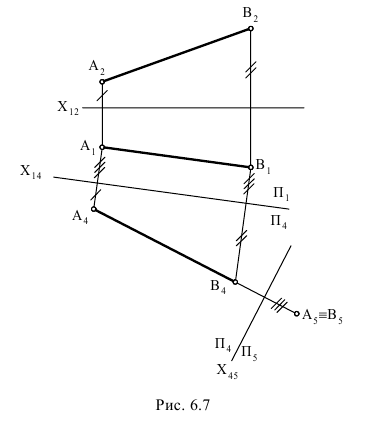
На рис. 6.8 приведен пример определения истинной величины треугольника 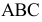 путем применения двух дополнительных плоскостей проекций.
путем применения двух дополнительных плоскостей проекций.
Заменяем систему плоскостей проекций 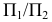 новой системой плоскостей проекций
новой системой плоскостей проекций 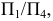 располагая плоскость проекций
располагая плоскость проекций 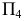 перпендикулярно треугольнику
перпендикулярно треугольнику 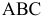 и плоскости проекций
и плоскости проекций 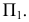 Это значит, что новая ось проекций должна быть расположена перпендикулярно горизонтальной проекции горизонтали
Это значит, что новая ось проекций должна быть расположена перпендикулярно горизонтальной проекции горизонтали 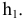 Плоскость треугольника в данном случае спроецируется на
Плоскость треугольника в данном случае спроецируется на 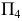 в прямую линию
в прямую линию 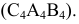
Чтобы получить истинную величину треугольника 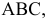 нужно плоскость
нужно плоскость 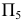 расположить параллельно плоскости треугольника
расположить параллельно плоскости треугольника 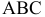 и перпендикулярно
и перпендикулярно 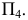 Это значит, что ось проекций
Это значит, что ось проекций 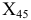 должна быть расположена параллельно проекции треугольника
должна быть расположена параллельно проекции треугольника 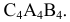 Полученная проекция
Полученная проекция 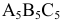 соответствует истинной величине треугольника
соответствует истинной величине треугольника 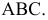
Метод вращения вокруг оси, перпендикулярной плоскости проекций
Сущность метода вращения вокруг оси, перпендикулярной плоскости проекций, состоит в том, что, сохраняя основную систему плоскостей проекций 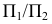 неизменной, проецируемым отрезкам прямых, плоским фигурам придаем путем вращения вокруг некоторой оси частное положение по отношению к плоскостям проекций. В том случае, если отрезок прямой повернуть до положения, параллельного плоскости проекций, то на эту плоскость проекций он спроецируется в натуральную величину.
неизменной, проецируемым отрезкам прямых, плоским фигурам придаем путем вращения вокруг некоторой оси частное положение по отношению к плоскостям проекций. В том случае, если отрезок прямой повернуть до положения, параллельного плоскости проекций, то на эту плоскость проекций он спроецируется в натуральную величину.
В качестве осей вращения применяют прямые, перпендикулярные плоскостям проекций, располагающиеся вне этих плоскостей или принадлежащие им (рис. 6.9).
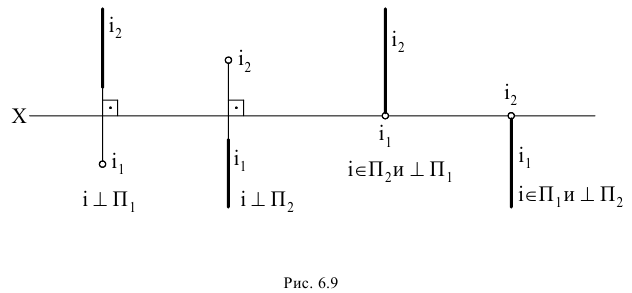
Рассмотрим пример на вращение точки 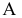 вокруг оси, перпендикулярной горизонтальной плоскости проекций. Пусть требуется точку
вокруг оси, перпендикулярной горизонтальной плоскости проекций. Пусть требуется точку 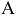 повернуть на некоторый угол
повернуть на некоторый угол 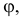 вращая по ходу часовой стрелки (рис. 6.10).
вращая по ходу часовой стрелки (рис. 6.10).
Ось вращения 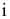 проецируется на горизонтальную плоскость проекций
проецируется на горизонтальную плоскость проекций 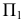 точкой
точкой 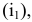 а на
а на 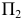 - прямой линией
- прямой линией 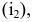 перпендикулярной оси
перпендикулярной оси 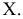 При вращении точки
При вращении точки 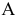 вокруг оси
вокруг оси 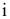 она будет перемещаться в плоскости
она будет перемещаться в плоскости 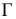 по окружности с радиусом
по окружности с радиусом 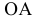 и центром вращения
и центром вращения 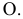 Плоскость
Плоскость 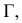 построенная дополнительно, располагается перпендикулярно оси
построенная дополнительно, располагается перпендикулярно оси 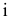 и называется плоскостью перемещения точки. Следовательно, горизонтальная проекция радиуса вращения
и называется плоскостью перемещения точки. Следовательно, горизонтальная проекция радиуса вращения 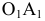 равняется истинной величине радиуса вращения
равняется истинной величине радиуса вращения 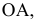 т.к. плоскости
т.к. плоскости 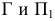 параллельны между собой. При вращении точки
параллельны между собой. При вращении точки 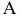 по ходу часовой стрелки на угол
по ходу часовой стрелки на угол 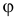 она переместится в плоскости
она переместится в плоскости 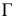 по дуге окружности радиуса
по дуге окружности радиуса 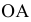 в точку
в точку 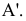 Горизонтальная проекция точки
Горизонтальная проекция точки 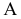 также будет перемещаться по окружности радиуса
также будет перемещаться по окружности радиуса 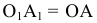 и займет положение
и займет положение 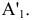 Фронтальная проекция
Фронтальная проекция 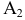 будет перемещаться по прямой, параллельной оси
будет перемещаться по прямой, параллельной оси 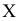 (след
(след 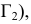 и займет положение
и займет положение 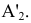
На рис. 6.11, а показан пример вращения точки 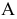 на угол
на угол 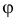 вокруг оси
вокруг оси 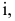 перпендикулярной
перпендикулярной 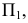 а на рис. 6.11, б - вращение точки
а на рис. 6.11, б - вращение точки 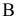 вокруг оси
вокруг оси 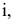 перпендикулярной
перпендикулярной 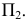
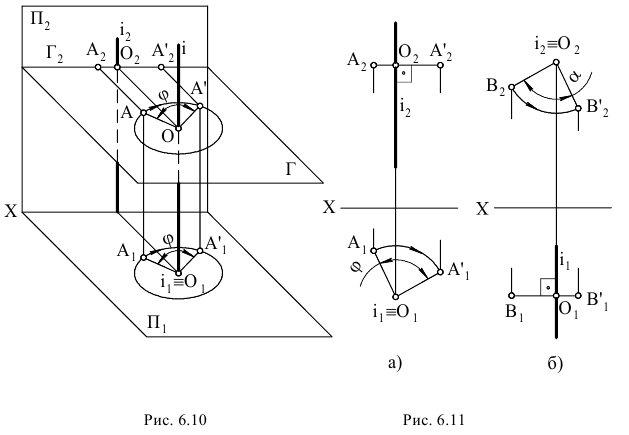
В первом случае горизонтальная проекция  точки
точки  перемещается по дуге радиусом
перемещается по дуге радиусом  до положения
до положения 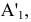 а фронтальная
а фронтальная 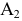 - по прямой линии, параллельной оси
- по прямой линии, параллельной оси 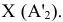 Во втором случае, наоборот, фронтальная проекция точки (точка
Во втором случае, наоборот, фронтальная проекция точки (точка 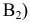 перемещается по дуге радиусом
перемещается по дуге радиусом 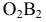 до положения
до положения 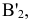 а горизонтальная - по прямой, параллельной оси
а горизонтальная - по прямой, параллельной оси 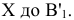
Рассмотрим примеры определения истинных величин геометрических образов методом вращения вокруг оси, перпендикулярной плоскости проекций.
Пусть требуется определить истинную величину отрезка 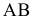 (рис. 6.12).
(рис. 6.12).
Целесообразно ось вращения проводить через одну из точек, принадлежащих отрезку, тогда получается более простое решение. В данной задаче ось 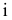 проходит через точку
проходит через точку 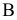 перпендикулярно горизонтальной плоскости проекций, следовательно, горизонтальная ее проекция совпадает с
перпендикулярно горизонтальной плоскости проекций, следовательно, горизонтальная ее проекция совпадает с 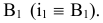 Перемещая горизонтальную проекцию точки
Перемещая горизонтальную проекцию точки 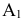 по дуге радиусом
по дуге радиусом 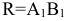 с центром вращения в точке
с центром вращения в точке 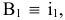 располагаем ее на таком расстоянии от оси
располагаем ее на таком расстоянии от оси 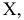 на котором расположена точка
на котором расположена точка 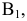 т.е. горизонтальная проекция отрезка
т.е. горизонтальная проекция отрезка 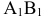 займет положение, параллельное оси
займет положение, параллельное оси 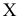
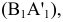 поэтому фронтальная проекция
поэтому фронтальная проекция 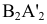 будет равняться истинной величине отрезка
будет равняться истинной величине отрезка 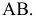 Как видно из чертежа, фронтальная проекция
Как видно из чертежа, фронтальная проекция 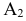 точки
точки 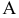 перемещается параллельно оси
перемещается параллельно оси 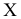 до пересечения с линией связи, проходящей от точки
до пересечения с линией связи, проходящей от точки 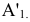
Определение истинной величины отрезка 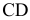 вращением вокруг оси, перпендикулярной фронтальной плоскости проекций, показано на рис. 6.13, где
вращением вокруг оси, перпендикулярной фронтальной плоскости проекций, показано на рис. 6.13, где 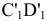 является истинной величиной отрезка
является истинной величиной отрезка 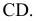
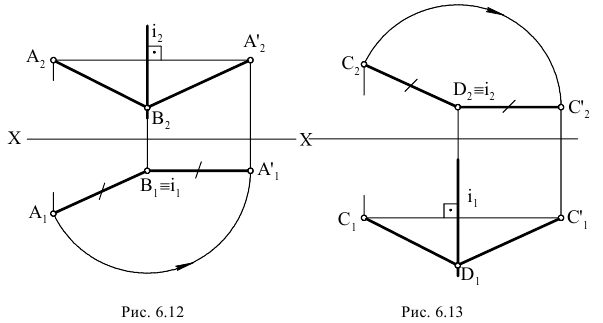
Как видно из рис. 6.14 и рис. 6.15, при вращении отрезка прямой вокруг оси, перпендикулярной 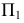 или
или 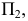 ее проекция на эту плоскость проекций остается неизменной. Учитывая это положение, предоставляется возможность решать аналогичные задачи без применения осей вращения, так называемым плоскопараллельным перемещением, при котором все точки прямой, фигуры перемещаются в плоскостях, параллельных между собой.
ее проекция на эту плоскость проекций остается неизменной. Учитывая это положение, предоставляется возможность решать аналогичные задачи без применения осей вращения, так называемым плоскопараллельным перемещением, при котором все точки прямой, фигуры перемещаются в плоскостях, параллельных между собой.
На рис. 6.14 определена истинная величина отрезка 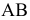 плоскопараллельным перемещением. Мысленно вращаем этот отрезок вокруг мнимой оси, перпендикулярной
плоскопараллельным перемещением. Мысленно вращаем этот отрезок вокруг мнимой оси, перпендикулярной 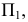 до положения, параллельного
до положения, параллельного 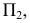 и располагаем горизонтальную проекцию
и располагаем горизонтальную проекцию 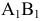 в произвольном месте параллельно оси
в произвольном месте параллельно оси 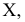 получаем отрезок
получаем отрезок 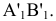 Фронтальные проекции точек
Фронтальные проекции точек 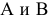 в данном случае перемещаются параллельно оси
в данном случае перемещаются параллельно оси 
На рис. 6.15 дан пример нахождения истинной величины отрезка 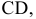 когда ось вращения
когда ось вращения 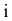 проходит перпендикулярно плоскости проекций
проходит перпендикулярно плоскости проекций 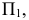 но не через отрезок
но не через отрезок 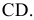 Из точки
Из точки 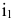 опускаем перпендикуляр
опускаем перпендикуляр 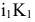 к горизонтальной проекции отрезка
к горизонтальной проекции отрезка 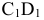 и вращаем этот перпендикуляр с проекцией отрезка
и вращаем этот перпендикуляр с проекцией отрезка 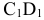 до положения, пока
до положения, пока 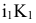 не расположится перпендикулярно оси
не расположится перпендикулярно оси 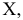 тогда отрезок
тогда отрезок 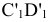 займет положение, параллельное оси
займет положение, параллельное оси 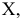 т.е. спроецируется на
т.е. спроецируется на 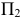 в истинную величину
в истинную величину 
При решении отдельных задач для достижения поставленной цели недостаточно применения одной оси вращения, тогда применяется несколько осей вращения. Так, при определении истинной величины треугольника  (рис. 6.16), занимающего общее положение относительно плоскостей проекций, необходимо его вначале повернуть до проецирующего положения, а затем - до плоскости уровня.
(рис. 6.16), занимающего общее положение относительно плоскостей проекций, необходимо его вначале повернуть до проецирующего положения, а затем - до плоскости уровня.
Ось вращения 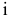 проводим перпендикулярно горизонтальной плоскости проекций, а в треугольнике
проводим перпендикулярно горизонтальной плоскости проекций, а в треугольнике 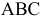 проводим горизонталь
проводим горизонталь 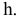 Вращаем эту горизонталь до проецирующего положения относительно плоскости проекций
Вращаем эту горизонталь до проецирующего положения относительно плоскости проекций 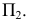 Горизонталь спроецируется в точку, а весь треугольник - в отрезок
Горизонталь спроецируется в точку, а весь треугольник - в отрезок 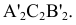
Вторую ось вращения 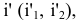 проходящую через точку
проходящую через точку 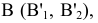 располагаем перпендикулярно плоскости проекций
располагаем перпендикулярно плоскости проекций 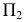 и вращаем треугольник
и вращаем треугольник 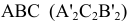 до положения, параллельного плоскости проекций
до положения, параллельного плоскости проекций 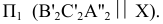 В этом случае горизонтальная проекция
В этом случае горизонтальная проекция 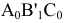 треугольника спроецируется в натуральную величину, т.е.
треугольника спроецируется в натуральную величину, т.е. 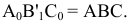
Вращение вокруг оси, параллельной плоскости проекций
При определении формы и размеров плоских фигур применение метода вращения вокруг оси, расположенной параллельно одной из плоскостей проекций (горизонтали, фронтали), значительно упрощает решение задач по сравнению с другими методами.
Пусть требуется точку 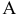 повернуть вокруг некоторой оси
повернуть вокруг некоторой оси 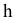 (рис. 7.1), расположенной параллельно плоскости проекций
(рис. 7.1), расположенной параллельно плоскости проекций 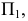 до положения, пока она не окажется на одном уровне с осью
до положения, пока она не окажется на одном уровне с осью 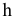 относительно
относительно 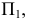 т.е. пока их расстояния до плоскости проекций
т.е. пока их расстояния до плоскости проекций 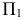 не окажутся одинаковыми.
не окажутся одинаковыми.
При вращении точки 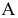 вокруг оси
вокруг оси 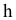 она будет перемещаться по окружности в плоскости
она будет перемещаться по окружности в плоскости 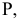 где
где 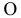 - центр вращения (точка пересечения оси с плоскостью
- центр вращения (точка пересечения оси с плоскостью 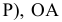 - радиус вращения. Плоскость
- радиус вращения. Плоскость 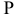 перпендикулярна оси вращения
перпендикулярна оси вращения 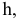 следовательно, она перпендикулярна и горизонтальной проекции
следовательно, она перпендикулярна и горизонтальной проекции 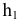 оси вращения
оси вращения 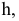 т.е. плоскость
т.е. плоскость 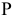 является горизонтально-проецирующей. Поэтому горизонтальная проекция точки
является горизонтально-проецирующей. Поэтому горизонтальная проекция точки 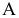 при вращении также будет перемещаться по горизонтальному следу
при вращении также будет перемещаться по горизонтальному следу 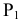 плоскости
плоскости 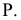 Чтобы была выполнена поставленная задача, необходимо вращать радиус
Чтобы была выполнена поставленная задача, необходимо вращать радиус 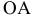 до тех пор, пока он не займет положение, параллельное горизонтальной плоскости проекций
до тех пор, пока он не займет положение, параллельное горизонтальной плоскости проекций 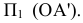 В этом случае точка
В этом случае точка 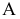 окажется на одинаковом уровне с осью
окажется на одинаковом уровне с осью 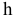 относительно плоскости проекций
относительно плоскости проекций 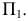 Тогда горизонтальная проекция радиуса вращения
Тогда горизонтальная проекция радиуса вращения 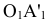 будет соответствовать натуральной величине радиуса вращения
будет соответствовать натуральной величине радиуса вращения 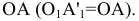
При определении нового положения точки  на чертеже (рис. 7.2) необходимо выполнить следующее: выбрать положение оси вращения
на чертеже (рис. 7.2) необходимо выполнить следующее: выбрать положение оси вращения 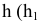
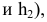 затем из горизонтальной проекции точки
затем из горизонтальной проекции точки 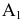 провести перпендикуляр к горизонтальной проекции оси вращения
провести перпендикуляр к горизонтальной проекции оси вращения 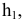 далее определить центр вращения
далее определить центр вращения 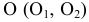 и радиус вращения
и радиус вращения 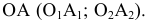 В заключение необходимо определить натуральную величину радиуса вращения
В заключение необходимо определить натуральную величину радиуса вращения 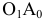 и отложить его величину от
и отложить его величину от 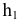 на продолжении перпендикуляра
на продолжении перпендикуляра 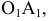 т.е. на горизонтальной проекции траектории перемещения точки
т.е. на горизонтальной проекции траектории перемещения точки 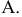 Получим горизонтальную проекцию
Получим горизонтальную проекцию 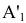 точки
точки 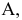 которая расположена на одном уровне с горизонталью, поэтому фронтальная проекция
которая расположена на одном уровне с горизонталью, поэтому фронтальная проекция 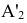 будет проецироваться на
будет проецироваться на 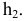
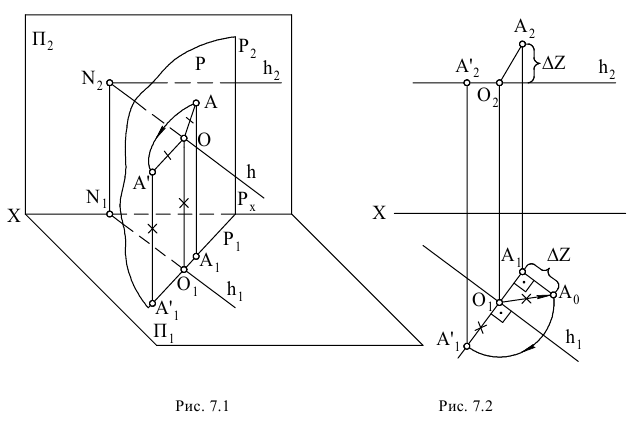
Рассмотрим пример построения натуральной величины треугольника 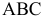 вращением вокруг горизонтали (рис. 7.3).
вращением вокруг горизонтали (рис. 7.3).
Сторона треугольника 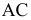 расположена параллельно горизонтальной плоскости проекций, поэтому проводим через нее горизонталь
расположена параллельно горизонтальной плоскости проекций, поэтому проводим через нее горизонталь 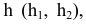 которая и будет являться осью вращения. Так как точки
которая и будет являться осью вращения. Так как точки 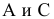 треугольника находятся на оси вращения, то при вращении они своего положения не меняют. Точка
треугольника находятся на оси вращения, то при вращении они своего положения не меняют. Точка 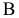 будет перемещаться в плоскости, перпендикулярной горизонтали, поэтому из горизонтальной проекции точки
будет перемещаться в плоскости, перпендикулярной горизонтали, поэтому из горизонтальной проекции точки 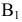 проводим прямую, перпендикулярную
проводим прямую, перпендикулярную 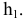 На пересечении этой прямой с
На пересечении этой прямой с 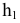 находится горизонтальная проекция центра вращения
находится горизонтальная проекция центра вращения 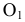 точки
точки 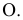 Фронтальная проекция
Фронтальная проекция 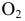 определена по линии связи и расположена она на
определена по линии связи и расположена она на 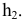 Радиусом вращения является отрезок
Радиусом вращения является отрезок 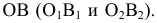 Определив натуральную величину радиуса вращения
Определив натуральную величину радиуса вращения 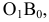 откладываем его на продолжении отрезка
откладываем его на продолжении отрезка 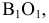 т.е. на горизонтальной проекции траектории перемещения точки
т.е. на горизонтальной проекции траектории перемещения точки 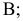 получим точку
получим точку 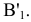 В таком положении радиус вращения
В таком положении радиус вращения 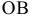 будет расположен параллельно
будет расположен параллельно 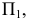 поэтому
поэтому 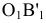 будет равняться
будет равняться 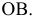 Соединив точку
Соединив точку 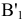 с точками
с точками 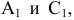 получим горизонтальную проекцию треугольника
получим горизонтальную проекцию треугольника 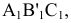 которая соответствует натуральной величине треугольника
которая соответствует натуральной величине треугольника 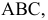 т.к. он в данном случае оказался параллельным
т.к. он в данном случае оказался параллельным 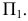 Фронтальная проекция треугольника проецируется на фронтальную проекцию горизонтали
Фронтальная проекция треугольника проецируется на фронтальную проекцию горизонтали 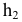
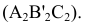
При необходимости поворота плоской фигуры параллельно фронтальной плоскости проекций нужно в качестве оси вращения выбрать фронталь, остальные построения аналогичны тем, что и при вращении вокруг горизонтали.
На рис. 7.4 показан поворот отрезка прямой  вокруг горизонтали
вокруг горизонтали 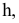 пересекающей данный отрезок в точке
пересекающей данный отрезок в точке 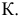 Точки
Точки 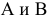 при вращении перемещаются в горизонтально-проецирующих плоскостях
при вращении перемещаются в горизонтально-проецирующих плоскостях 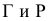 (следы
(следы 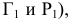 поэтому из горизонтальных проекций точек
поэтому из горизонтальных проекций точек 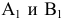 проводим прямые, перпендикулярные горизонтальной проекции горизонтали. На пересечении этих прямых с
проводим прямые, перпендикулярные горизонтальной проекции горизонтали. На пересечении этих прямых с 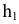 получим горизонтальные проекции
получим горизонтальные проекции 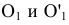 центров вращения. Проекциями радиусов вращения являются отрезки
центров вращения. Проекциями радиусов вращения являются отрезки 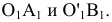
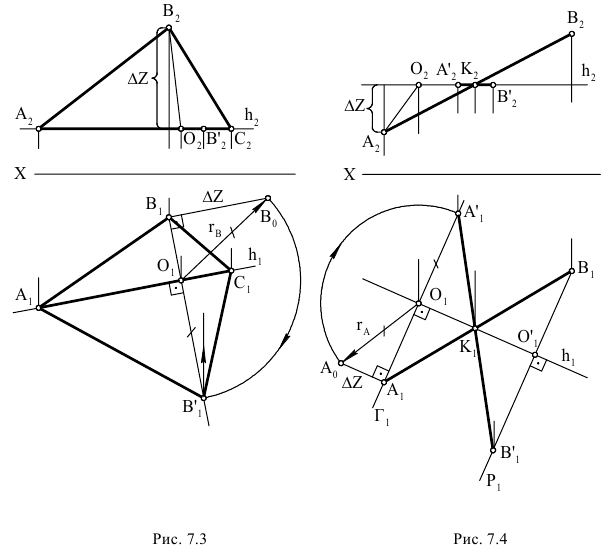
Так как точка 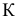 расположена на пересечении отрезка
расположена на пересечении отрезка  и горизонтали
и горизонтали  то при вращении отрезка она остается на месте. Достаточно определить натуральную величину одного радиуса вращения
то при вращении отрезка она остается на месте. Достаточно определить натуральную величину одного радиуса вращения 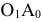 и отложить его величину на следе
и отложить его величину на следе 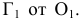 Получим точку
Получим точку 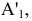 которую соединяем прямой с проекцией точки
которую соединяем прямой с проекцией точки 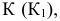 и продолжаем ее до пересечения со следом
и продолжаем ее до пересечения со следом 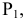 проходящим перпендикулярно от точки
проходящим перпендикулярно от точки 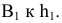
Полученная проекция отрезка 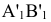 является натуральной величиной отрезка
является натуральной величиной отрезка 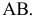 Фронтальная его проекция
Фронтальная его проекция 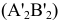 спроецируется на фронтальную проекцию горизонтали
спроецируется на фронтальную проекцию горизонтали 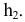
Вращение вокруг следа плоскости
Вращение плоскости вокруг следа этой плоскости находит применение в тех случаях, когда необходимо, например, определить истинную величину отрезка прямой, плоской фигуры и др., расположенных в данной плоскости. Чтобы добиться этой цели, необходимо плоскость вращать вокруг ее следа до совмещения с одной из плоскостей проекций, 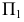 или
или 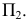 Этот способ еще называется способом совмещения, так как здесь плоскость пространства совмещается (накладывается) с какой-либо плоскостью проекций.
Этот способ еще называется способом совмещения, так как здесь плоскость пространства совмещается (накладывается) с какой-либо плоскостью проекций.
Пусть требуется плоскость 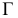 совместить с плоскостью проекций
совместить с плоскостью проекций  вращая ее вокруг горизонтального следа
вращая ее вокруг горизонтального следа  (рис. 7.5, а).
(рис. 7.5, а).
Учитывая, что горизонтальный след 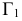 плоскости
плоскости 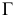 является осью вращения, то при вращении он, а вместе с ним и точка схода следов
является осью вращения, то при вращении он, а вместе с ним и точка схода следов 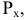 своего положения не меняют, т.е. остаются на месте. Чтобы найти совмещенное положение фронтального следа
своего положения не меняют, т.е. остаются на месте. Чтобы найти совмещенное положение фронтального следа 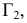 достаточно найти хотя бы еще одну точку в совмещенном положении, принадлежащую следу
достаточно найти хотя бы еще одну точку в совмещенном положении, принадлежащую следу 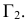 Второй точкой будет являться точка схода следов
Второй точкой будет являться точка схода следов 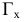 плоскости
плоскости 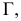 так как она принадлежит одновременно фронтальному и горизонтальному следам этой плоскости.
так как она принадлежит одновременно фронтальному и горизонтальному следам этой плоскости.
Для решения задачи возьмем на фронтальном следе 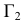 в произвольном месте точку
в произвольном месте точку 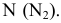 При вращении она будет перемещаться по окружности в плоскости
При вращении она будет перемещаться по окружности в плоскости 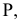 перпендикулярной горизонтальному следу
перпендикулярной горизонтальному следу 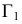 плоскости
плоскости 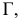 т.е. оси вращения. Центром вращения является точка
т.е. оси вращения. Центром вращения является точка 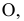 а радиусом вращения -
а радиусом вращения - 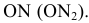 Проведя дугу радиусом
Проведя дугу радиусом 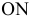 до пересечения с
до пересечения с 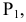 получим точку
получим точку 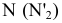 в совмещенном положении. Соединив точку
в совмещенном положении. Соединив точку 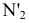 с точкой схода следов
с точкой схода следов 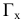 прямой линией, получим совмещенное положение фронтального следа
прямой линией, получим совмещенное положение фронтального следа 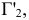 а, следовательно, и всей плоскости
а, следовательно, и всей плоскости 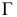 с плоскостью проекций
с плоскостью проекций 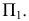 Следует отметить, что при вращении плоскости
Следует отметить, что при вращении плоскости 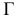 вокруг горизонтального следа отрезок
вокруг горизонтального следа отрезок 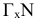 не изменяет своей величины, поэтому совмещенное положение точки
не изменяет своей величины, поэтому совмещенное положение точки 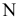 с плоскостью
с плоскостью 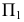 можно найти, если из точки схода следов
можно найти, если из точки схода следов 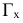 сделать засечку радиусом
сделать засечку радиусом 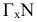 на следе
на следе 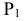 (траектория перемещения точки
(траектория перемещения точки 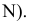
Такое решение приведено на рис. 7.5, б, где из точки схода следов 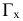 проведена дуга радиусом
проведена дуга радиусом 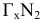 до пересечения с прямой, перпендикулярной
до пересечения с прямой, перпендикулярной 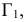 проходящей от точки
проходящей от точки 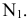
На рис. 7.6 приведено решение задачи на совмещение плоскости 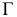 и точки
и точки 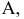 принадлежащей этой плоскости, с плоскостью проекций
принадлежащей этой плоскости, с плоскостью проекций 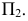
Первоначально проводим в плоскости 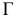 через точку
через точку 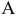 фронталь
фронталь 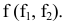 Затем находим совмещенное положение плоскости
Затем находим совмещенное положение плоскости 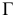 с плоскостью
с плоскостью 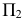 и совмещенное положение фронтали
и совмещенное положение фронтали 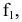 на которой отмечаем совмещенную точку
на которой отмечаем совмещенную точку 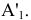
Построение истинной величины треугольника 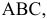 расположенного в плоскости общего положения
расположенного в плоскости общего положения 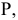 приведено на рис. 7.7. В данном случае плоскость
приведено на рис. 7.7. В данном случае плоскость 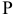 с находящимся в ней треугольником
с находящимся в ней треугольником 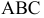 совмещена с горизонтальной плоскостью проекций
совмещена с горизонтальной плоскостью проекций 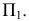 Для этого применены горизонтали, проходящие через вершины треугольника. При их совмещении с горизонтальной плоскостью проекций они пройдут параллельно горизонтальному следу
Для этого применены горизонтали, проходящие через вершины треугольника. При их совмещении с горизонтальной плоскостью проекций они пройдут параллельно горизонтальному следу 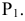 Точки же
Точки же 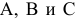 треугольника
треугольника 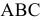 будут перемещаться перпендикулярно горизонтальному следу
будут перемещаться перпендикулярно горизонтальному следу 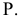 На пересечении этих линий с горизонталями и будут находиться вершины совмещенного треугольника
На пересечении этих линий с горизонталями и будут находиться вершины совмещенного треугольника 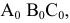 который равняется истинной величине треугольника
который равняется истинной величине треугольника 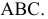
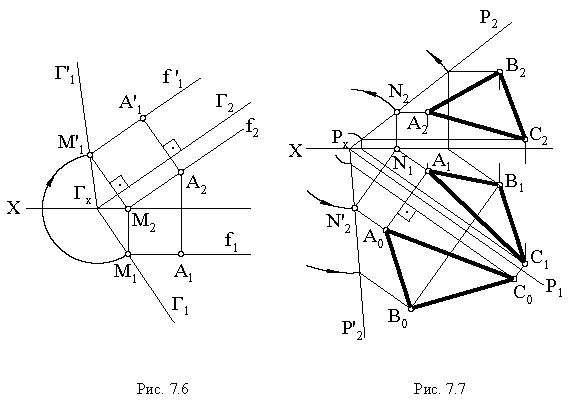
В том случае, если имеется совмещенное положение плоскости 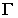
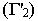 с плоскостью проекций
с плоскостью проекций 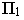 и совмещенное положение отрезка
и совмещенное положение отрезка 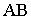
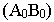 (рис. 7.8, а), а необходимо построить (восстановить) фронтальный след плоскости
(рис. 7.8, а), а необходимо построить (восстановить) фронтальный след плоскости 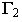 и проекции отрезка
и проекции отрезка 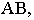 т.е. выполнить действие, обратное совмещению, необходимо первоначально определить положение недостающею следа плоскости в системе плоскостей проекций
т.е. выполнить действие, обратное совмещению, необходимо первоначально определить положение недостающею следа плоскости в системе плоскостей проекций 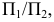 затем найти проекции отрезка.
затем найти проекции отрезка.
Чтобы определить положение следа 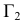 на его совмещенном положении
на его совмещенном положении 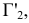 в произвольном месте возьмем точку
в произвольном месте возьмем точку 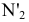 и найдем ее фронтальную проекцию
и найдем ее фронтальную проекцию 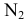 (рис. 7.8, б). Для чего из точки
(рис. 7.8, б). Для чего из точки 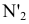 проводим перпендикуляр к горизонтальному следу
проводим перпендикуляр к горизонтальному следу 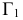 до пересечения с осью
до пересечения с осью 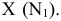 Из точки
Из точки 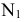 восстанавливаем перпендикуляр к оси
восстанавливаем перпендикуляр к оси 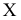 до пересечения с дугой радиуса
до пересечения с дугой радиуса 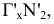 получим точку
получим точку 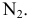 Через точку схода следов
Через точку схода следов 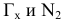 проводим фронтальный след плоскости
проводим фронтальный след плоскости 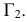 Затем через точку
Затем через точку 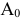 проводим совмещенную горизонталь и на ее проекции наносим проекции
проводим совмещенную горизонталь и на ее проекции наносим проекции 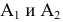 точки
точки 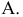
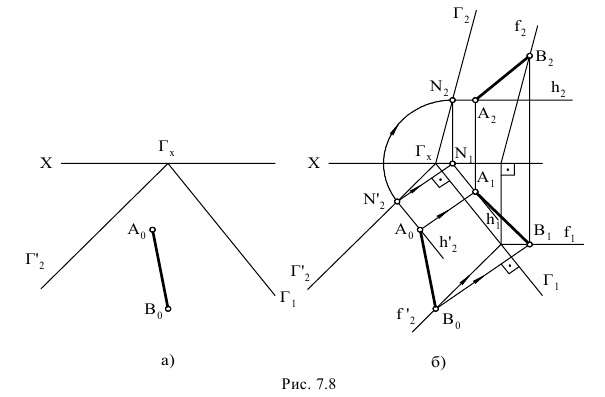
Для определения проекций точки 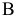 воспользуемся фронгалью
воспользуемся фронгалью 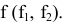 В совмещенном попоженнн проводим ее через точку
В совмещенном попоженнн проводим ее через точку 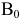 параллельно совмещенному фронтальному следу
параллельно совмещенному фронтальному следу 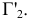 Затем находим проекции фронтали
Затем находим проекции фронтали 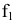 и
и 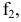 как указано на чертеже, и по линиям связи определяем проекции
как указано на чертеже, и по линиям связи определяем проекции 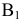 и
и 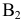 точки
точки 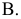 Соединив
Соединив 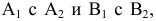 получим необходимые проекции отрезка
получим необходимые проекции отрезка 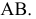
Решение метрических задач методом преобразования чертежа
1. Определить расстояние между двумя параллельными отрезками прямых 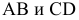 методом замены плоскостей проекций (рис. 7.9).
методом замены плоскостей проекций (рис. 7.9).
Для решения данной задачи необходимо выполнить двойную замену плоскостей проекций. При первой замене новую плоскость проекций (ось 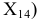 располагаем параллельно данным отрезкам и перпендикулярно плоскости проекций
располагаем параллельно данным отрезкам и перпендикулярно плоскости проекций 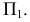 В новой системе плоскостей проекций
В новой системе плоскостей проекций 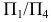 отрезки прямых преобразуются в отрезки уровня и на
отрезки прямых преобразуются в отрезки уровня и на  проецируются в натуральную величину. Вторую плоскость проекций располагаем перпендикулярно одновременно
проецируются в натуральную величину. Вторую плоскость проекций располагаем перпендикулярно одновременно 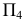 и отрезкам
и отрезкам 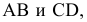 которые проецируются на нее в точки
которые проецируются на нее в точки 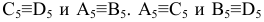 будет искомым расстоянием между данными отрезками прямых линий.
будет искомым расстоянием между данными отрезками прямых линий.
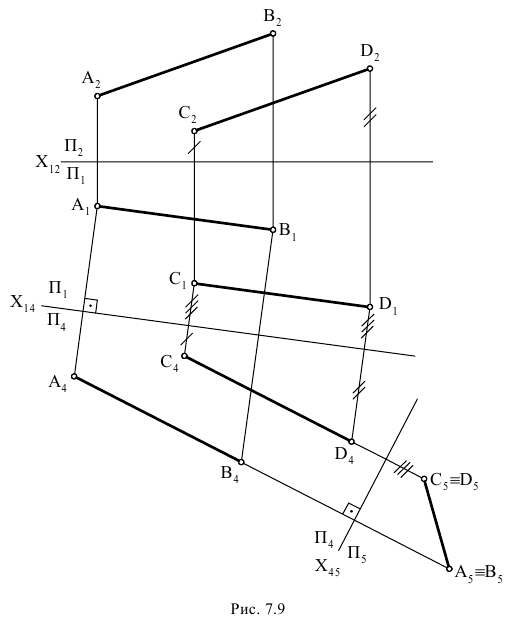
Определить расстояние от точки 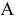 до прямой
до прямой 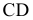 методом плоскопараллельного перемещения (рис. 7.10).
методом плоскопараллельного перемещения (рис. 7.10).
Объединив точку 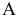 в одну плоскость с отрезком
в одну плоскость с отрезком 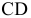 (на рис. не показано), располагаем эту систему плоскопараллельным перемещением, как вращением вокруг оси, перпендикулярной
(на рис. не показано), располагаем эту систему плоскопараллельным перемещением, как вращением вокруг оси, перпендикулярной 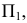 так, чтобы отрезок занял положение, параллельное плоскости проекций
так, чтобы отрезок занял положение, параллельное плоскости проекций 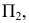 при этом не изменяя величину отрезка и взаимного положения точки
при этом не изменяя величину отрезка и взаимного положения точки 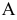 и отрезка
и отрезка  Фронтальную проекцию
Фронтальную проекцию  получим при помощи линий связи и линий перемещения, которые проходят параллельно оси
получим при помощи линий связи и линий перемещения, которые проходят параллельно оси 
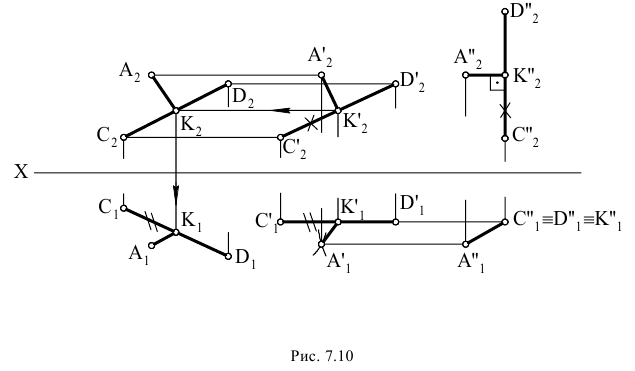
Второе вращение (плоскопараллельное перемещение) выполняем параллельно 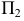 и отрезок
и отрезок 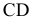 располагаем параллельно
располагаем параллельно 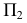 и перпендикулярно
и перпендикулярно 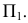
В данном случае отрезок 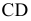 спроецируется в точку
спроецируется в точку 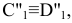 а точка
а точка 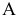 - в точку
- в точку 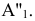 Расстояние между проекциями
Расстояние между проекциями 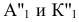 и есть расстояние от точки
и есть расстояние от точки 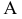 до отрезка
до отрезка 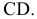 Фронтальная проекция точки
Фронтальная проекция точки 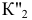 определена при помощи прямой, проходящей от
определена при помощи прямой, проходящей от 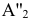 параллельно оси
параллельно оси 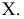 Так как
Так как 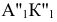 является истинным расстоянием от точки
является истинным расстоянием от точки 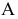 до отрезка
до отрезка 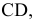 то фронтальная проекция
то фронтальная проекция 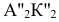 должна быть параллельна оси
должна быть параллельна оси 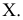 На рис. 7.10 также показаны все проекции расстояния
На рис. 7.10 также показаны все проекции расстояния 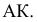
3. Определить угол наклона прямой 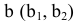 к плоскости общего положения
к плоскости общего положения 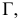 заданной следами
заданной следами 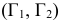 (рис. 7.11).
(рис. 7.11).
С целью упрощения решения задачи при определении угла наклона прямой b 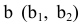 к плоскости
к плоскости 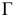 воспользуемся методом определения дополнительного угла мезду этой прямой и перпендикуляром, проведенным из произвольной точки
воспользуемся методом определения дополнительного угла мезду этой прямой и перпендикуляром, проведенным из произвольной точки 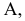 расположенной на прямой
расположенной на прямой 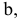 к плоскости
к плоскости 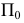 (рис. 7.12). Как видно из рис. 7.12, угол
(рис. 7.12). Как видно из рис. 7.12, угол 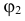 можно определить из прямоугольного треугольника
можно определить из прямоугольного треугольника 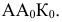 Он равняется:
Он равняется: 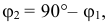 где
где 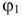 - дополнительный угол мезду прямой
- дополнительный угол мезду прямой 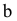 и перпендикуляром
и перпендикуляром 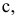 проведенным к плоскости
проведенным к плоскости 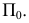
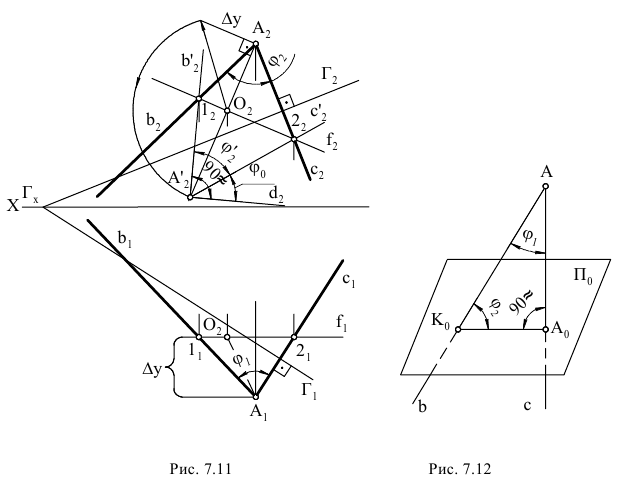
Для определения угла наклона прямой 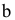 к плоскости
к плоскости 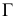 (см рис. 7.11) проводим из течки
(см рис. 7.11) проводим из течки 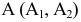 перпендикуляр к плоскости
перпендикуляр к плоскости 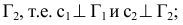 получаем проекции угла, который дсполняет до
получаем проекции угла, который дсполняет до 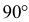 искомьй угол между прямой
искомьй угол между прямой 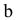 и плоскостью
и плоскостью 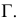
Проведя фронталь 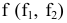 в произвольном месте, но так, чтобы она пересекала прямые
в произвольном месте, но так, чтобы она пересекала прямые 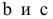 и вращая дополнительный угол
и вращая дополнительный угол 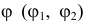 при вершине
при вершине 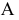 до положения, параллельного плоскости проекций
до положения, параллельного плоскости проекций 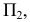 определим его истинную величину
определим его истинную величину 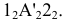 Затем, дополняя его до
Затем, дополняя его до 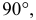 получим угол
получим угол 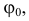 который равняется
который равняется 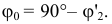 Этот дополнительный угол и есть угол наклона прямой
Этот дополнительный угол и есть угол наклона прямой 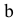 к плоскости
к плоскости 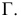
| Рекомендую подробно изучить предметы: |
| Ещё лекции с примерами решения и объяснением: |