Способ вспомогательных сфер в начертательной геометрии с примером

Способ вспомогательных сфер:

Этот способ широко используется при решении задач на построе­ние линий пересечения поверхностей вращения с пересекающимися осями.

Прежде чем перейти к рассмотрению этого способа, рассмотрим частный случай пересечения поверхностей вращения, у которых оси совпадают. Такие поверхности называются соосными поверхностями вращения.

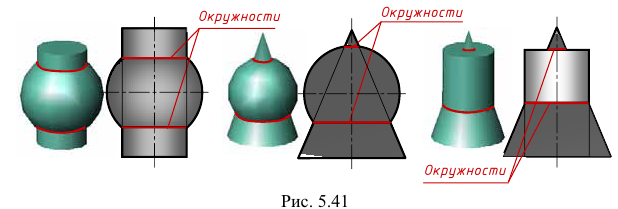
Линия пересечения соосных поверхностей - окружность, плос­кость которой перпендикулярна оси поверхностей вращения. При этом, если ось поверхностей вращения параллельна плоскости проекций, то линия пересечения на эту плоскость проецируется в отрезок прямой ли­нии (рис. 5.41).

Это свойство используют для построения линии взаимного пересечения двух поверхностей вращения с помощью вспомогательных сфер. При этом могут быть использованы концентрические (построенные из одного центра) и эксцентрические (проведенные из разных цен­тров) сферы. Рассмотрим применение вспомогательных концентрических сфер - сфер с постоянным центром.

Следует отметить, что если плоскость осей поверхностей враще­ния не параллельна плоскости проекций, то окружности, по которым пересекаются поверхности, будут проецироваться в эллипсы, а это усложняет решение задачи. Поэтому способ вспомогательных сфер следует применять при следующих условиях:

• а) пересекающиеся поверхности должны быть поверхностями вращения;
• б) оси этих поверхностей должны пересекаться, точку пересечения принимают за центр вспомогательных сфер;
• в) плоскость, образованная осями поверхностей (плоскость сим­метрии), должна быть параллельна одной из плоскостей проекций.

Используя этот способ, можно построить линию пересечения по­верхностей на одной проекции.

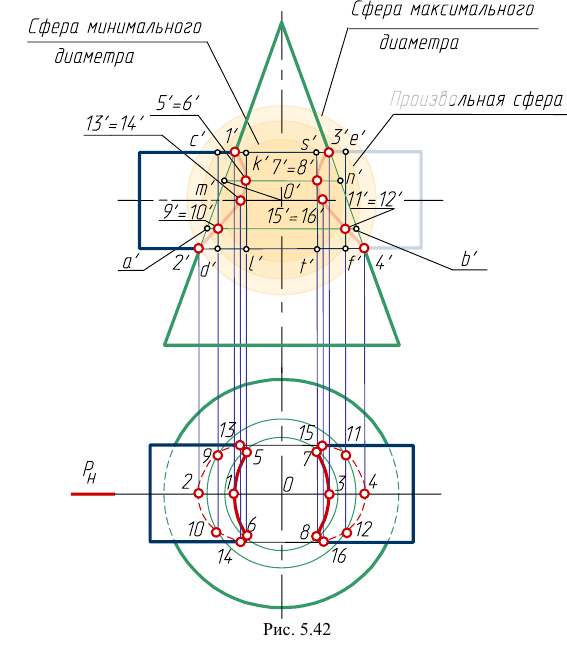
Рассмотрим пример построения линии пересечения цилиндра и конуса вращения (рис. 5.42).

Точки 1, 2, 3, 4 определяются как точки пересечения контурных образующих поверхностей, принадлежащие плоскости пересечения осей (плоскости симметрии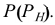

Из точки пересечения осей данных поверхностей (точки О') построим вспомогательную сферу произвольного радиуса. Эта сфера будет одновременно соосна конусу и цилиндру и пересечет их по окруж­ностям. Плоскости этих окружностей перпендикулярны соответствующим осям вращения. Фронтальные проекции этих окружностей - отрез­ки прямых. Проведенная сфера пересекает конус по окружности диаметра 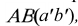а цилиндр - по окружностям 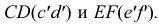В пересечении окружности АВ с окружностями CD и EF получаем соответственно точки 9-10 и 1 1-12, принадлежащие линии пересечения.

Таким образом, можно построить достаточное количество точек искомой линии пересечения. При этом нужно иметь ввиду, что не все сферы могут быть использованы для решения задачи. Рассмотрим предельные границы вспомогательных сфер.

Радиус максимальной секущей сферы будет равен расстоянию от центра о' до самой удаленной точки пересечения контурных образующих (от точки о' до точек 2' и 4')- Минимальной секущей сферой долж­на быть такая сфера, которая касалась бы одной поверхности (большей) и пересекала вторую (меньшую). В данном примере минимальная сфера касается поверхности конуса по окружности 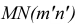и пересекает ци­линдр по окружностям 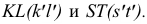Пересекаясь между собой, ок­ружности MN и KL дают точки линии пересечения 5 (5') и 6 (6'), а окружности MN и ST - точки 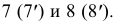Это самые глубокие точки линии пересечения.

Для точности решения между максимальной и минимальной сфе­рами необходимо построить дополнительные (промежуточные) сферы: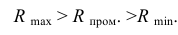

Если дополнительная сфера пересекает только одну данную поверхность, то такая сфера для решения задачи непригодна.

Для построения второй проекции линии пересечения можно ис­пользовать окружности, полученные от сечения конуса вспомогательными сферами.

Можно также построить дополнительные сечения поверхности, Точки 13-14 и 15-16, лежащие на контурных образующих цилиндра, являются точками границы видимости линии пересечения на горизонтальной проекции.