Сопряжение линий и лекальные кривые на чертежах с примерами

Содержание:

Сопряжение линий и лекальные кривые:

Сопряжения применяются во многих деталях машин для плавного перехода линий.

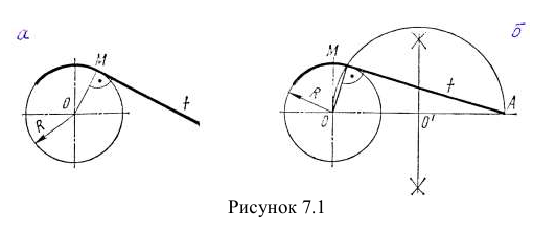
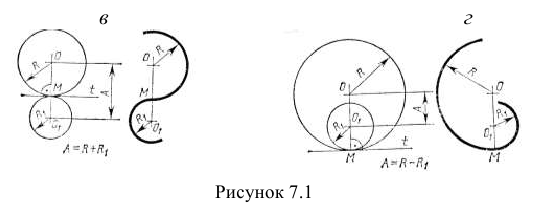
Для построения сопряжений необходимо уметь строить касательную в данной точке окружности (рисунок 7.1 а) проводить из внешней точки прямую, касательную к окружности (рисунок 7.1 б). Помнить, что центры окружностей, соприкасающихся внешним образом, находятся на расстоянии суммы их радиусов (рисунок 7.1 в), а внутренним - на расстоянии их радиусов (рисунок 7.1 г), причем точка касания (сопряжения) всегда лежит на прямой, проходящей через их центры.

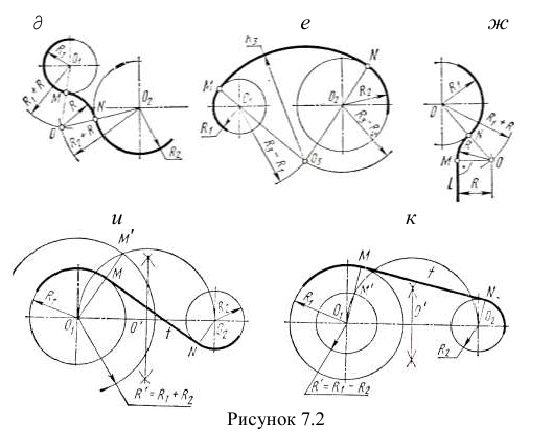
Изложенное позволяет легко уяснить последовательность решений задач на сопряжения, приведенных ни рисунке 7.2. д, е, ж, и, к.

Лекальные кривые обводят при помощи лекал. Наиболее часто применяют в технике следующее:

Эллипс

Эллипсом называется замкнутая кривая, для которой сумма расстояний от любой точки до двух точек - фокусов эллипса - есть величина постоянная. Для построения  эллипса проводят две концентрические окружности, диаметры которых равны осям эллипса (рисунок 7.3). Эти окружности делят на несколько равных частей (12-16). Через точки деления на большей окружности проводят вертикальные линии, через соответствующие точки деления на малой окружности - горизонтальные линии. Пересечение этих линий даст точки эллипса I, II, III

• Заказать чертежи

Парабола

Параболой называется кривая, каждая точка которой расположена на одинаковом расстоянии от заданной прямой, носящей название директрисы, и точки, называемой фокусом параболы.

Даны вершина параболы О, одна из точек параболы D  и направление оси ОС (рисунок 7.4).

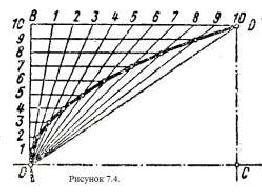
На отрезках ОС  и CD строят прямоугольник, стороны  этого прямоугольника ОВ  и BD делят на произвольное одинаковое число равных частей и нумеруют точки деления согласно рис. Вершину О соединяют с точками деления стороны BD, а из точек деления отрезка ОВ  проводят прямые, параллельные оси. Пересечение прямых, проходящих через точки с одинаковыми номерами, определяет ряд точек параболы (другие способы построения параболы см. в рекомендуемой литературе).

Циклоида

Траектория точки А, принадлежащей окружности, перекатываемой без скольжения по прямой, называется циклоидой (рисунок 7.5). Для ее построения от исходного положения точки А на направляющей прямой откладывают отрезок 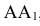, равный длине данной окружности - 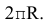. Окружность и отрезок 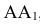делят на одинаковое число равных частей.

Восставляя перпендикуляры из точек деления прямой 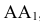до пересечения с прямой, проходящей через центр данной окружности параллельно 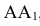, намечают ряд последовательных положений центра перекатываемой окружности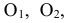 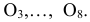. Описывая из этих центров окружности радиуса R, отмечают точки пересечения с ними прямых, проходящих параллельно 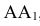через точки деления окружности 1, 2, 3, 4 и т.д.

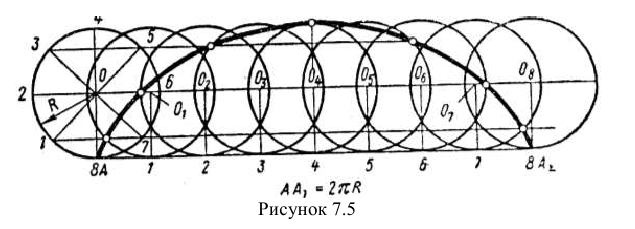
В пересечении горизонтальной прямой, проходящей через точку 1, с окружностью, описанной из центра 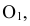находится одна из точек циклоиды; в пересечении прямой, проходящей через точку 2, с окружностью, проведенной из центра 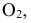находится другая точка циклоиды и т.д. Соединяя полученные точки плавной кривой, получаем циклоиду.

Синусоида

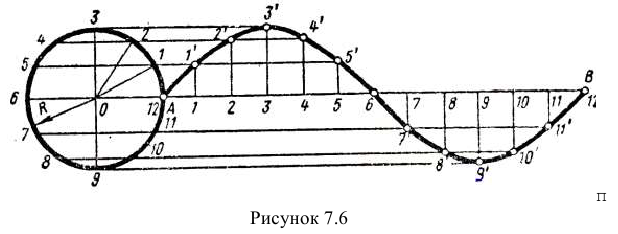
Для построения синусоиды делят окружность заданного радиуса на равные части (6, 8, 12, и т.д.) и на продолжении осевой линии от условного начала - точки А - проводят отрезок прямой АВ, равный 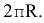 Затем прямую делят на такое же число равных частей, как и окружность (6, 8, 12 и т. д.)

Из точек окружности 1, 2, 3, 12 проводят прямые линии параллельно выбранной прямой до пересечения с соответствующими перпендикулярами, восстановленными или опущенными из точек деления прямой. Полученные точки пересечения 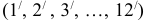и будут точками синусоиды с периодом колебания, равным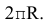

Эвольвента (развертка круга)

Эвольвентой называется траектория, описываемая каждой точкой прямой линии, перекатываемой по окружности без скольжения.

В машиностроении по эвольвенте очерчивают профиль головок зубьев зубчатых колес.

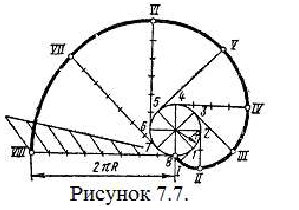
Для построения эвольвенты окружность предварительно делят на произвольное число п равных частей; в точках деления проводят касательные к окружности, направленные в одну сторону. На касательной, проведенной через последнюю точку деления, откладывают отрезок, равный длине окружности 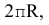, и делят его на то же число n равных частей. Откладывая на первой одно деление равное 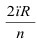, на второй - два, на третьей - три и т.д., получают ряд точек I, II, III, IV и т.д., которые соединяют по лекалу.