Соотношения между сторонами и углами треугольника с примерами

Соотношения между сторонами и углами треугольника:

Можно заметить, что в треугольнике длины сторон связаны с величинами противолежащих углов следующим образом: большей стороне соответствует больший противолежащий угол, а меньшей стороне — меньший. Так, в треугольнике ABC сторона АС — большая, сторона АВ — средняя, сторона ВС — меньшая,

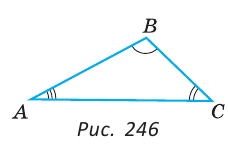
Эта гипотеза находит подтверждение в следующей теореме.

Теорема (о соотношениях между сторонами и углами в треугольнике).

В треугольнике против большей стороны лежит больший угол, а против большего угла лежит большая сторона.

Теорема состоит из двух утверждений. Докажем каждое из них.

1) В треугольнике против большей стороны лежит больший угол.

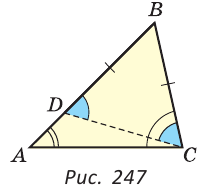
Дано: АВС, АВ > ВС (рис. 247).

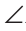Доказать: C >A.

Доказательство:

На большей стороне ВА от вершины В отложим отрезок BD, равный меньшей стороне ВС, и проведем отрезок CD. Получим равнобедренный ADBC, у которого углы при основании равны, то есть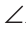BDC =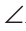BCD. Но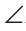BDC — внешний для треугольника ADC, и поэтому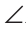BDC больше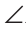A. Значит, и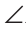BCD больше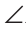A. А так как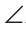C больше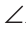BCD, то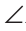C подавно больше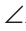A. Утверждение доказано.

2) В треугольнике против большего угла лежит большая сторона.

Дано: АВС, C >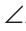A (рис. 248).

Доказать: АВ > ВС.

Доказательство:

Применим метод доказательства от противного. ПустьC >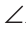A, а АВ < ВС. Если АВ < ВС, то по первой части теоремы 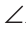C <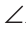A. Получили противоречие с условием. Если АВ = ВС, то АВС — равнобедренный, и тогда 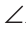    A =C. Снова получили противоречие. Следовательно, АВ > ВС. Утверждение доказано.

Следствие 1.

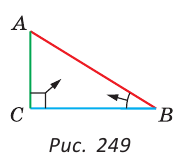
Катет прямоугольного треугольника меньше гипотенузы.

Следствие 1 справедливо, так как катет лежит против острого угла, а гипотенуза — против прямого, который больше острого (рис. 249).

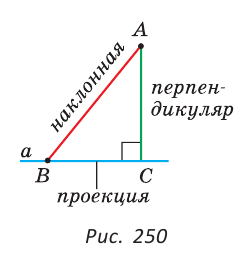
Определение. Если АС — перпендикуляр к прямой 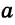, точка В принадлежит прямой а и не совпадает с точкой С, то отрезок АВ называется наклонной, проведенной из точки А к прямой 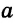(рис. 250). Точка В называется основанием наклонной. Отрезок ВС, соединяющий основание наклонной и основание перпендикуляра, называется проекцией наклонной АВ на прямую .

Следствие 2.

Если из одной точки к прямой проведены перпендикуляр и наклонная, то перпендикуляр и проекция наклонной меньше этой наклонной.

Следствие 2 справедливо, поскольку в прямоугольном треугольнике катет меньше гипотенузы.

Определение. Расстоянием от точки до прямой называется длина перпендикуляра, опущенного из точки на прямую.

Если точка лежит на прямой, то это расстояние равно нулю.

Из следствия 2 вытекает, что длина перпендикуляра, опущенного из данной точки на прямую, — это кратчайшее расстояние от данной точки до точек прямой.

На рисунке 251, а расстояние от точки М до прямой равно длине перпендикуляра МК.

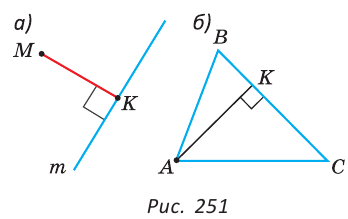
Расстояние от вершины А треугольника ABC до прямой ВС, содержащей противоположную сторону, равно высоте АК треугольника (рис. 251, б).

В математике за расстояние между фигурами принимается наименьшее расстояние между точками этих фигур.

Пример:

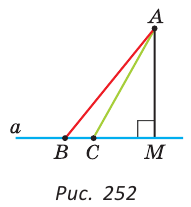
Отрезок AM — перпендикуляр к прямой 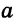. Точки В и С лежат на прямой а по одну сторону от точки М (рис. 252). Доказать, что если СМ < ВМ, то АС <АВ.

Доказательство:

Так как АМС — прямоугольный, то 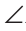ACM — острый. Тогда смежный к нему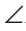ACB — тупой. В треугольнике ABC угол АСВ — больший, поэтому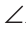ACB >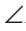ABC. Так как в треугольнике против большего угла лежит большая сторона, то АС <АВ. Что и требовалось доказать.

Замечание. Решите данную задачу при условии, что точки В и С лежат на прямой 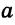по разные стороны от точки М. Тогда будет доказано свойство: «Если наклонные проведены из одной точки к одной прямой, то большей проекции соответствует большая наклонная, а меньшей — меньшая».

Пример:

Дан равнобедренный прямоугольный треугольник с гипотенузой 12 см. Найти расстояние от вершины прямого угла до прямой, содержащей гипотенузу.

Решение:

Пусть в АВС АС=ВС, 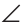С=90^о, АВ=12 см (рис.253). По свойству равнобедренного треугольник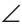а А =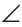В = 45^о. Проведем высоту СК. Длина отрезка СК - искомое расстояние. В равнобедренном треугольнике АСВ высота СК, опущенная на основание АВ, будет медианой и биссектрисой.

Поэтому АК=КВ=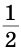АВ=6 см, 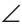АСК=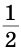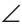АСВ=45^о.

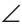В прямоугольном АСК АСК=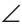САК=45^о. Поэтому АСК - равнобедренный и СК=АК=6 см.

Ответ: 6 см.

Замечание. В дальнейшем будем пользоваться тем, что высота равнобедренного прямоугольного треугольника, проведенная к гипотенузе, равна половине гипотенузы.

Сумма градусных мер углов треугольника. Внешний угол треугольника

Докажем теорему о сумме градусных мер углов треугольника.

Теорема 1 (теорема о сумме градусных мер углов треугольника). Сумма градусных мер углов треугольника равна 180°.

Доказательство.

1) Пусть ABC — произвольный треугольник. Докажем, что A + B + C= 180°.

2) Проведем через вершину В прямую а, параллельную стороне АС (рис. 103, а).

3) Углы 1 и 4 являются внутренними накрест лежащими углами, образованными при пересечении параллельных прямых АС и а секущей AB, значит, 1= 4 (теорема 3, глава 4, § 2).

4) Углы 3 и 5 являются внутренними накрест лежащими углами, образованными при пересечении параллельных прямых АС и а секущей ВС, следовательно, 3 = 5.

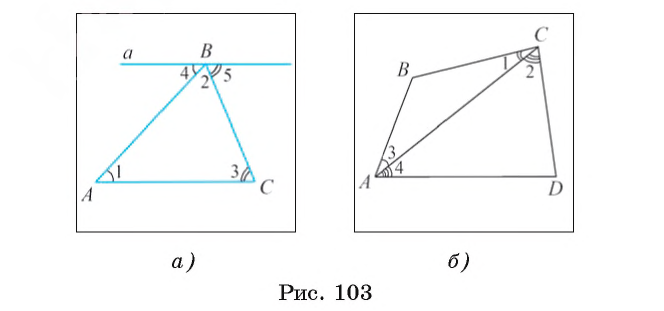
5) Сумма градусных мер углов 4, 2 и 5 равна градусной мере развернутого угла с вершиной в точке B, т. е. 4+2+5= 180°. Но так как 1 = 4 и 3 = 5, то получаем: 3+2+1= 180°, т. е. A + B + C = 180°.

Теорема доказана.

Например, пусть ABC и ADC — два треугольника, имеющие общую сторону АС и лежащие в разных полуплоскостях с границей АС, тогда ABC + BCD + CDA + DAB = 360° (рис. 103, б). Действительно,ABC + BCD + CDA + DAB = ABC + (I + 2) + CDA + (3 + 4) = (ABC + 1 + 3) + (CDA +2 + 4) = 180° + 180° = 360°.

Определение. Внешним углом треугольника называется угол, смежный с каким-либо углом треугольника.

Например, 1 — внешний угол треугольника ABC, смежный с углом ВСА, a 2 — внешний угол, смежный с углом ВАС (рис. 104, а).

Теорема 2 (о внешнем угле треугольника). Градусная мера внешнего угла треугольника равна сумме градусных мер двух углов треугольника, не смежных с ним.

Доказательство.

1) Пусть ABC — произвольный треугольник. Докажем, например, что градусная мера внешнего угла 4 равна сумме градусных мер не смежных с ним углов 1 и 2 (рис. 104, б).

2) Так как сумма градусных мер углов 3 и 4 равна градусной мере развернутого угла, то 3 + 4 = 180°, а по теореме о сумме градусных мер углов треугольника (l + 2) +3 = 180°, следовательно, 4 = 1 + 2.

Теорема доказана.

Из теоремы о сумме градусных мер углов треугольника следует, что если в треугольнике один из углов прямой или тупой, то сумма градусных мер двух других углов не больше 90°, следовательно, каждый из них острый. Отсюда вытекает, что в любом треугольнике либо все углы острые, либо два угла острые, а третий тупой или прямой.

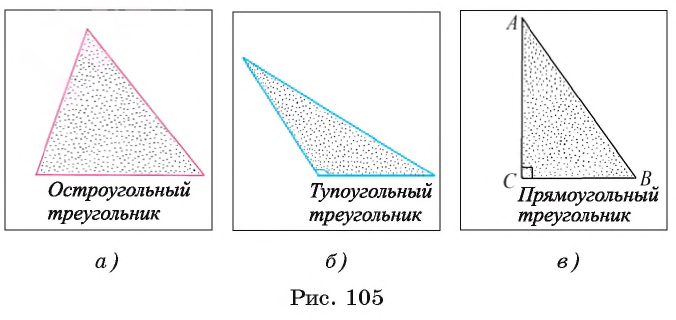
Треугольник называется остроугольным, если все его углы острые (рис. 105, а). Треугольник называется тупоугольным, если один из его углов тупой (рис. 105, б). Треугольник называется прямоугольным, если один из его углов прямой (рис. 105, в).

Из определения прямоугольного треугольника и теоремы о сумме градусных мер углов треугольника следует, что сумма градусных мер острых углов прямоугольного треугольника равна 90°.

Стороны прямоугольного треугольника имеют специальное название. Сторона прямоугольного треугольника, лежащая против прямого угла, называется гипотенузой, а две другие стороны — катетами. Например, на рисунке 105, в изображен прямоугольный треугольник ABC с прямым углом С. Сторона AB этого треугольника является гипотенузой, а стороны АС и ВС — катетами.

Две модели прямоугольного треугольника получаются, если лист бумаги, имеющий форму прямоугольника, разрезать, как показано на рисунке 106, а.

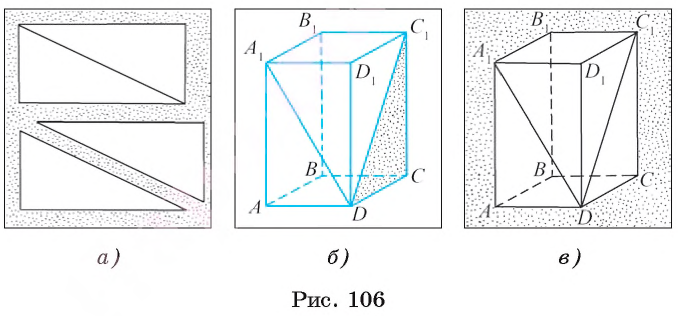
На рисунке 106, б, в изображены прямоугольные треугольники А₁AD и DCC1, которые содержатся соответственно в гранях AА₁D₁D  и DD₁C₁C  прямоугольного параллелепипеда.