Соотношения между сторонами и углами произвольного треугольника с примерами решения

Содержание:

Соотношения между сторонами и углами произвольного треугольника:

Теорема синусов

В этом параграфе докажем теорему синусов, которая позволяет находить длины неизвестных сторон треугольника, если известна длина одной стороны и градусные меры двух углов, а также вычислять градусные меры углов, если известны длины двух сторон и градусная мера угла, лежащего против одной из этих сторон.

Предварительно докажем следующую теорему, которая позволяет находить площадь треугольника, если известны длины двух его сторон и градусная мера угла между ними. Данная теорема может быть применена при решении многих задач.

Теорема 1 (о нахождении площади треугольника через длины двух сторон и синус угла между ними). Площадь треугольника равна половине произведения длин двух его сторон на синус угла между ними.

Доказательство.

Пусть в треугольнике ABC известны градусная мера угла А и АВ = с, АС = Ъ. Докажем, что площадь данного треугольника можно найти по формуле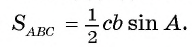

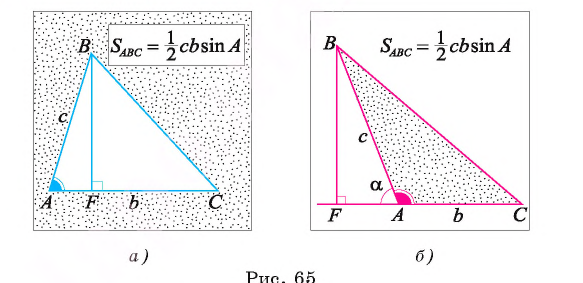
1) Пусть угол А — острый (рис. 65, а), а отрезок BF — высота треугольника. Тогда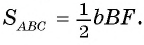

В прямоугольном треугольнике ABF длина катета BF = с sin А. Таким образом,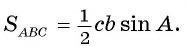

2) Пусть угол А — тупой (рис. 65, б). 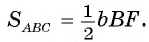 В прямоугольном треугольнике ABF длина катета BF = с sin а, где 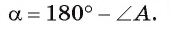Так как то 

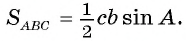
Таким образом, в каждом из случаев 1) и 2)площадь треугольника равна половине произведения длин двух его сторон на синус угла между ними.

3) Если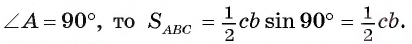

Теорема доказана.

Воспользуемся утверждением этой теоремы для доказательства теоремы синусов.

Теорема 2 (теорема синусов). Длины сторон треугольника пропорциональны синусам противолежащих углов.

2)    Отсюда следует, что выполняются равенства: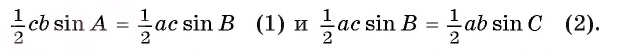

3) Из равенства (1) следует, что 6 sin А = a sin В. Отсюда

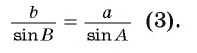
4) Из равенства (2) следует, что с sin В = b sin С. Отсюда получим, что

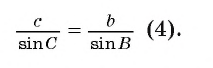
Из равенств (3)    и    (4) следует, что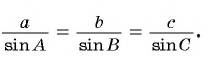  

Теорема доказана.

3) Таким образом,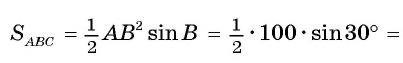

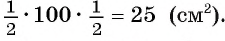
Пример:

В треугольнике ABC длина стороны АС равна 4 см, 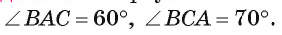Вычислите длины сторон АВ и ВС (рис. 68).

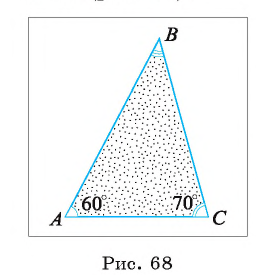
Решение:

Для вычисления длин сторон воспользуемся теоремой синусов.

1) Пусть АВ = х и ВС = у. Тогда по теореме синусов 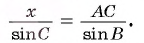  Отсюда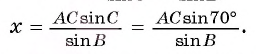  

Сумма градусных мер углов треугольника равна 180°, следовательно, 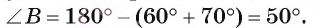. По таблице значений тригонометрических функций (см. Приложение) найдем 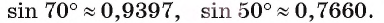. Таким образом,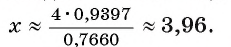 

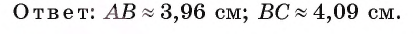
Пример:

В треугольнике ABC градусная мера угла В равна 40°, а длины сторон ВС и АС равны 8 см и 6 см соответственно. Вычислите градусные меры углов А, С и длину стороны АВ.

Решение:

По теореме синусов выполняется равенство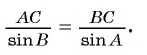 
Отсюда следует, что 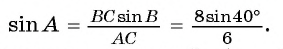значений тригонометрических функций (см. Приложение)

найдем 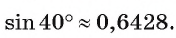Следовательно,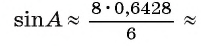

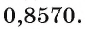
Этому значению синуса соответствуют два угла: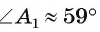 

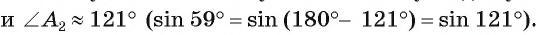
1). В случае 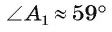найдем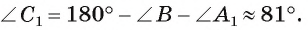 

Теперь найдем длину стороны: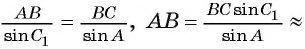 

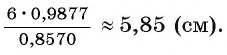
2). Если 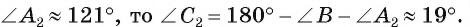В этом случае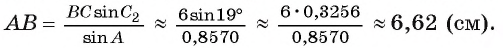 

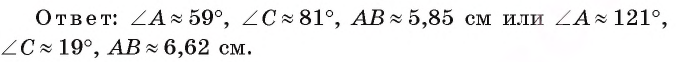
Теорема косинусов

1. Теорема косинусов. В данном параграфе докажем теорему, которая связывает длины трех сторон треугольника и косинус одного из его углов. Эта теорема называется теоремой косинусов и формулируется следующим образом.

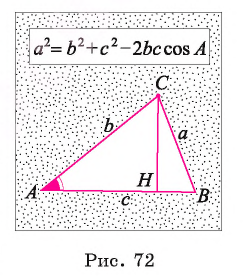
Теорема 1 (теорема косинусов). Квадрат длины любой стороны треугольника равен сумме квадратов длин двух других его сторон без удвоенного произведения длин этих сторон на косинус угла между ними.

Доказательство.

1) Пусть отрезок СН — высота треугольника ABC, угол А — острый, АС =

= b, СВ = а, АВ = с (рис. 72).

2) В прямоугольном треугольнике АСB найдем СН = b sin А, АН = b cos А, ВН =

= с - b cos А.

3) Воспользуемся теоремой Пифагора для треугольника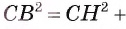

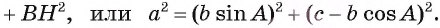
Отсюда получим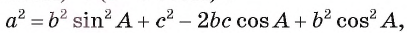 

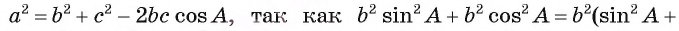
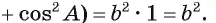
Нетрудно доказать, что формула верна и в случае, когда угол А — тупой. В этом случае проведите доказательство самостоятельно.

Если угол А — прямой, то теорема косинусов представляет собой теорему Пифагора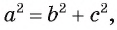, так как в этом случае cos А = cos 90° = 0.

Теорема доказана.

Аналогично квадраты длин сторон бис выражаются соответственно формулами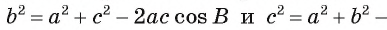 

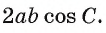
Пример:

В треугольнике ABC АВ = 5 см, ВС = 7 см, АС = 8 см. Докажите, что градусная мера угла, лежащего против стороны ВС, равна 60°.

Доказательство.

По теореме косинусов верно равенство 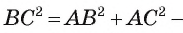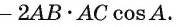Следовательно, 49 = 25 + 64 - 2 • 5 • 8 cos А.

Отсюда найдем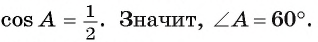

Что и требовалось доказать.

Пример:

В параллелограмме ABCD 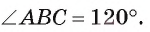 Биссектриса угла В пересекает сторону AD параллелограмма в точке F, AF = 3 см и FD = 2 см. Вычислите длину отрезка BF и длину диагонали АС параллелограмма.

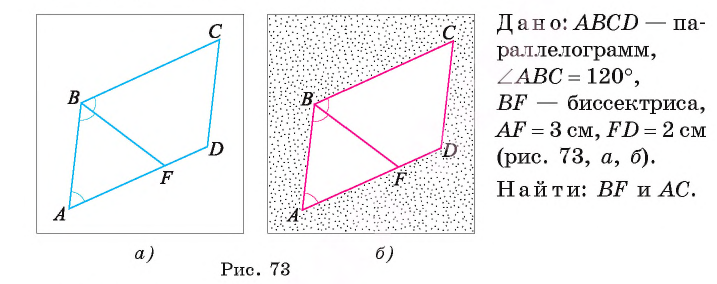
Решение:

1) Рассмотрим треугольник ABF. Так как BF — биссектриса угла ABC и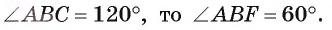 Сумма градусных мер углов, прилежащих к одной стороне параллелограмма, равна 180°, следовательно,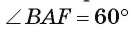. Так как сумма градусных мер углов треугольника равна 180°, то 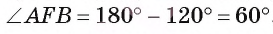Таким образом, в треугольнике ABF градусная мера каждого угла равна 60°, т. е. этот треугольник — равносторонний и BF = AF = АВ = 3 см.

2) Для вычисления длины диагонали АС воспользуемся теоремой косинусов. В треугольнике ABC по теореме косинусов запишем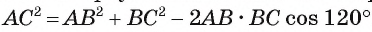. Так к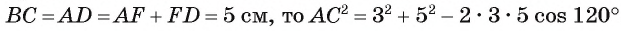ак . Так

как 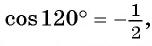   то    отсюда    найдем АС = 7 см.

Ответ: BF = 3 см, АС = 7 см.

Теорема косинусов позволяет доказать ряд утверждений, которые полезны при решении многих задач. Докажем некоторые из таких утверждений.

Пример:

Докажите, что если а, b и с — длины сторон треугольника ABC, то длины его медиан 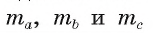могут быть найдены по формулам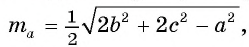 

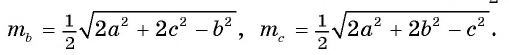
Доказательство.

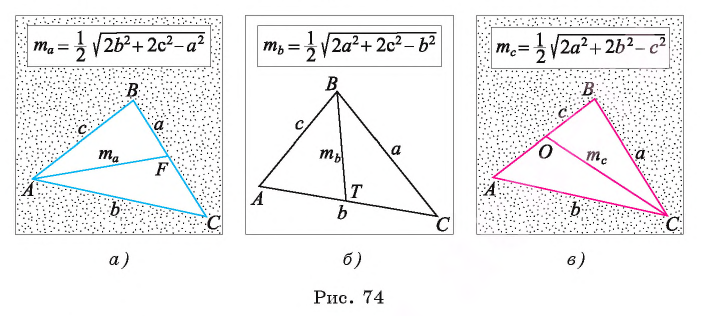
Докажем, например, первую формулу. Пусть отрезок AF — медиана треугольника ABC, АВ = с, АС = b, ВС = а (рис. 74, а).

Применим теорему косинусов для треугольника ABF, в котором 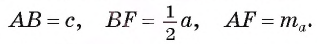Можем записать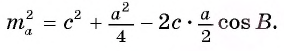. По теореме косинусов для треугольника ABC имеем 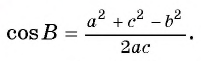Таким образом, получим  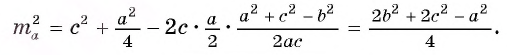 Отсюда следует, что 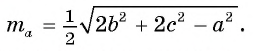. Доказательство двух других формул проведите самостоятельно (рис. 74, б, в). Заметим, что при доказательстве указанных формул можно воспользоваться следующей задачей.

Пример:

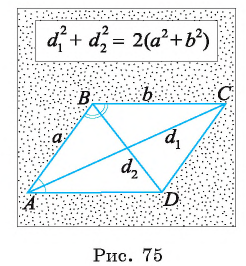
Пусть 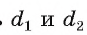— длины диагоналей параллелограмма, а и b — длины его сторон. Докажите, что сумма квадратов длин диагоналей параллелограмма равна сумме квадратов длин его сторон, т. е.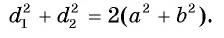

Доказательство.

Пусть в параллелограмме ABCD АВ = а, ВС = 6,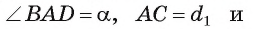 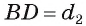(рис. 75).

По теореме косинусов для треугольника ABD справедливо равенство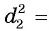

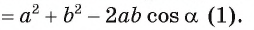
Для треугольника ABC по теореме косинусов 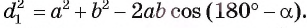. Так как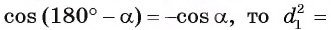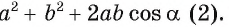. Сложив равенства (1) и (2) почленно, получим 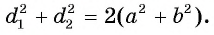Что и требовалось доказать.

Пример:

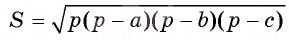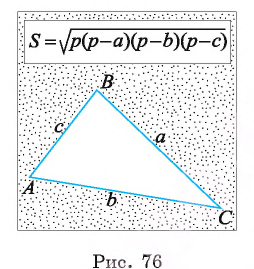
Докажите, что площадь любого треугольника можно найти по формуле (формула Герона), где а, b и с — длины сторон треугольника, а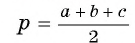 — его полупериметр (рис. 76).

Доказательство.

Пусть в треугольнике ABC АВ = с, ВС = а, АС = b.

По теореме косинусов верно равенство: 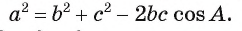Отсюда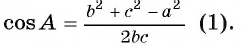 

Так как площадь треугольника 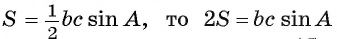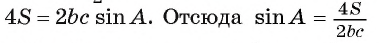Учитывая равенства (1) и (2) и равенство  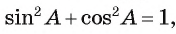получим 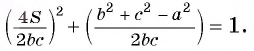ОТсюда  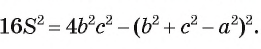Используя формулу разности квадратов двух выражений, преобразуем правую часть полученного равенства следующим образом:

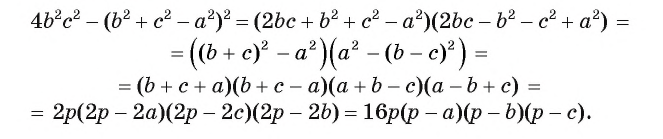
Значит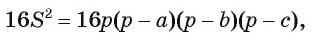 

следовательно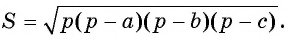 

Что и требовалось доказать.

Пример:

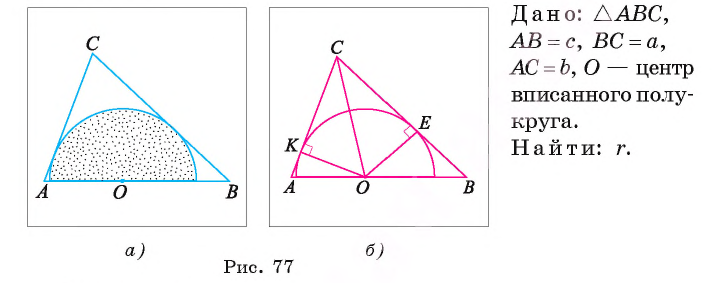
В треугольнике ABC АВ = с, ВС = а и АС = Ь. Найдите радиус г полукруга, вписанного в данный треугольник, если центр О полукруга принадлежит стороне АВ (рис. 77, а).
 

Решение:

1) Пусть полукруг касается сторон АС и СВ в точках К и Е соответственно. Соединим центр О с точками К,СиЕ (рис. 77, б).

2) Радиус, проведенный в точку касания, перпендикулярен касательной, значит, отрезки ОК и ОЕ являются высотами треугольников АОС и ВОС соответственно. Площадь 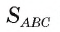треугольника АБС равна сумме площадей треугольников АОС и ВОС. Следовательно,

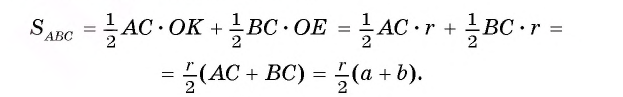
Отсюда получим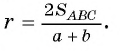 

3) По формуле Герона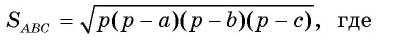 

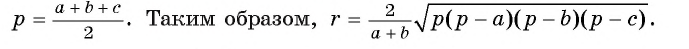
Ответ: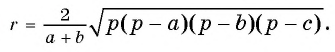 

Решение треугольников

Решить треугольник — значит по трем его элементам найти другие его элементы. Приведем примеры задач на решение треугольника.

Пример: (нахождение элементов треугольника по длинам двух сторон и градусной мере угла между ними).

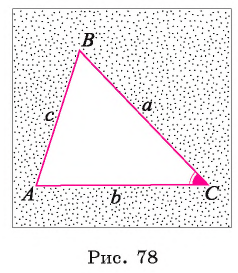
Известны длины а и Ъ двух сторон ВС и АС треугольника и градусная мера а угла между ними. Найдите неизвестные элементы треугольника (рис. 78).

Решение:

Ответ: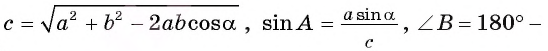 

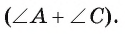
Пример: (нахождение элементов треугольника по длине стороны и градусным, мерам двух прилежащих к ней углов).

Известны длина а стороны ВС треугольника ABC и градусные меры у и р двух прилежащих к ней углов. Найдите неизвестные элементы треугольника.