Соотношения между синусом, косинусом, тангенсом и котангенсом одного и того же угла (тригонометрические тождества)

Содержание:

Установим соотношения между синусом, косинусом, тангенсом и котангенсом одного и того же угла.

Основное тригонометрическое тождество

Так как центром единичной окружности является начало координат, а ее радиус равен 1 (рис. 72), то уравнение единичной окружности имеет вид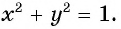

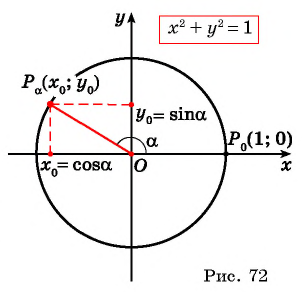
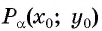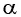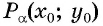Координаты любой точки единичной окружности удовлетворяют уравнению этой окружности. По определению синуса и косинуса угла точка имеет координаты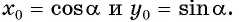

Подставим координаты точки 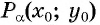в уравнение единичной окружности и получим формулу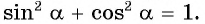

Формула основного тригонометрического тождества

Полученную формулу называют основным тригонометрическим тождеством, а также тригонометрической единицей.

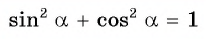
С помощью основного тригонометрического тождества, зная значения синуса (косинуса) угла 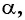можно найти косинус (синус) этого же угла.

Например, найдем 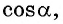если известно, что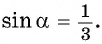

Для этого из формулы 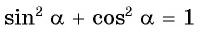выразим 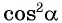и получим 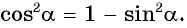Так как 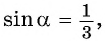то найдем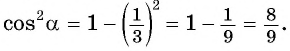

Тогда 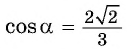или 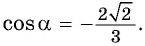Знак 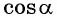зависит от того, в какой четверти находится угол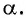

Пример №1

Известно, что 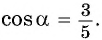Найдите 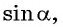если

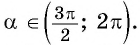
Решение:

Из основного тригонометрического тождества 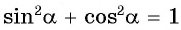выразим 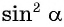и получим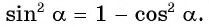

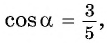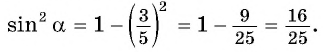По условию тогда Значит,

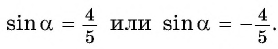
По условию 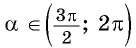(четвертая четверть), тогда 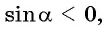значит,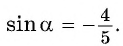

Ответ: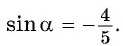

По определению тангенса угла 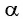получим формулу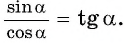

Формула 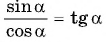справедлива для всех углов 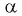таких, что 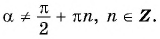Поскольку при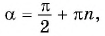 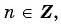абсцисса соответствующих точек единичной окружности равна нулю, то 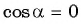при 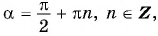т. е. дробь 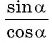при этих значениях а не имеет смысла.

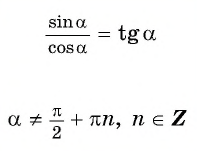
По определению котангенса угла 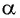получим формулу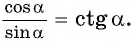

Формула 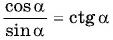справедлива для всех углов 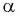таких, что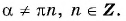

Поскольку при 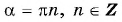ордината соответствующих точек единичной окружности равна нулю, то 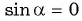при 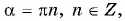т. е. дробь 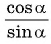при этих значениях 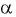не имеет смысла.

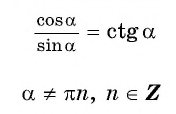
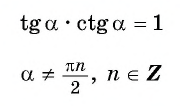
Поскольку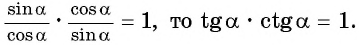

Формула 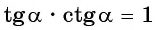справедлива для всех углов 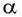таких, что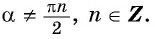

Разделим обе части основного тригонометрического тождеств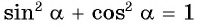а на 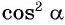и получим:

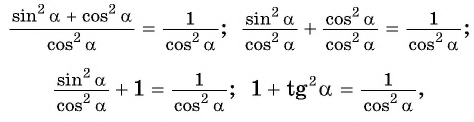где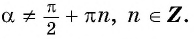

Разделив обе части основного тригонометрического тождества на 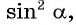получим формулу

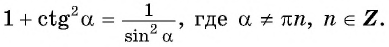
Формулы (тригонометрические тождества), которые мы вывели, описывают соотношения между синусом, косинусом, тангенсом и котангенсом одного и того же угла.

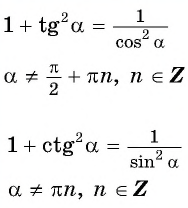
Полученные формулы позволяют находить значения 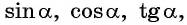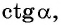если одно из этих значений известно.

Пример №2

Найдите значения 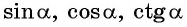угла 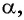если

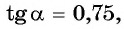
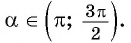
Решение:

Из формулы 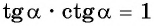выразим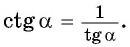

Так как по условию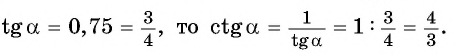

По формуле 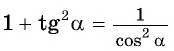найдем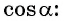

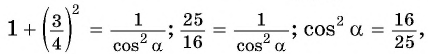значит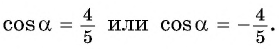

Так как 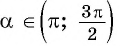(третья четверть), то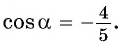

Из формулы 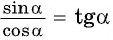выразим 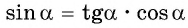и найдем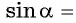

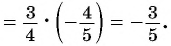
Ответ: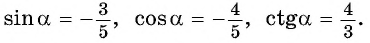

Рассмотрим, как тригонометрические тождества используются для упрощения выражений.

Пример №3

Упростите выражение:

Решение:

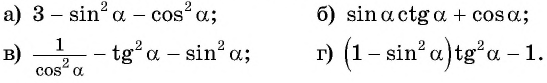
• Заказать решение задач по высшей математике

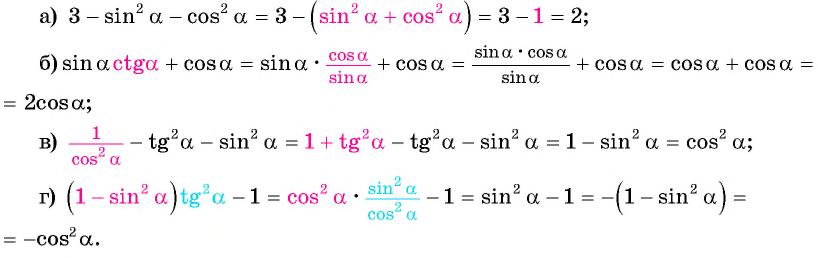
Примеры заданий и их решения

Пример №4

Могут ли синус и косинус одного угла быть равными соответственно: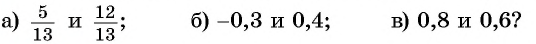

Решение:

Для ответа на вопрос достаточно проверить, верно ли равенство 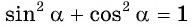(т. е. выполняется ли условие принадлежности точки 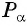единичной окружности).

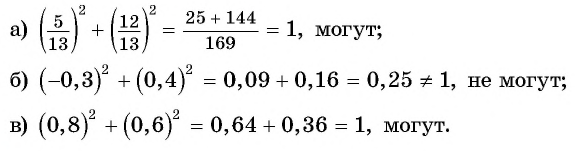
Пример №5

Найдите: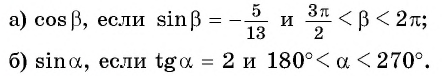

Решение:

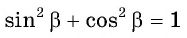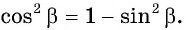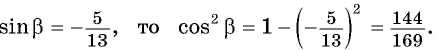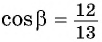а) Из равенства выразим Так как Тогда или 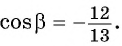Поскольку 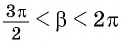(угол четвертой четверти), то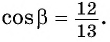

б) Так как 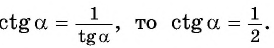Из формулы 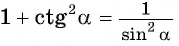найдем 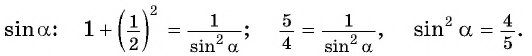Так как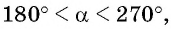

а значения синуса угла в третьей четверти отрицательны, то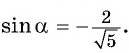

Пример №6

Упростите выражение:

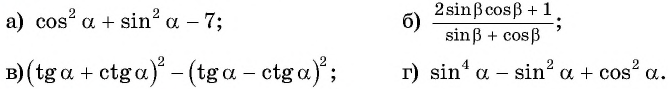
Решение:

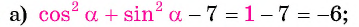
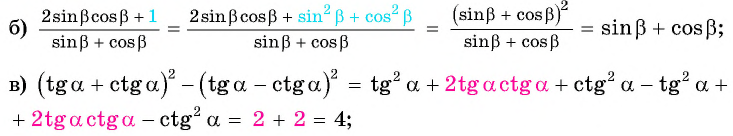
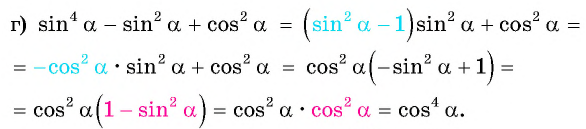
Пример №7

Найдите значение выражения: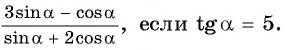

Решение:

Известно, что 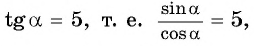тогда

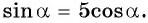
Значит,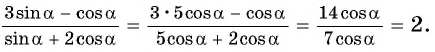

Если 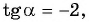то: