
Сочлененные системы в теоретической механике
Сочлененные системы:
Сочлененной называется система нескольких тел, соединенных друг с другом при помощи внутренних связей: простого опирания, стержней или нитей (цепей), шарниров.
При решении некоторых задач с сочлененными системами равновесие каждого тела системы рассматривают отдельно. При этом в месте сочленения тел возникают две силы, одна из которых приложена к одному телу, а другая — ко второму телу. Эти силы равны по модулю, направлены вдоль одной прямой, но в противоположные стороны (закон равенства действия и противодействия).
На рис. 126 показаны силы взаимодействия, возникающие между телами A и В: 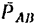
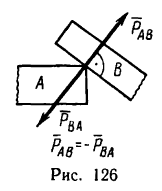
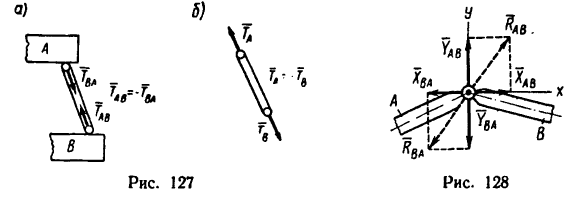
На рис. 127 показаны силы, возникающие при взаимодействии тел A и В не непосредственно друг с другом, а через стержень. Если допустить, что тело A действует на В через стержень силой 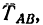 , то тогда со стороны тела В возникнет сила
, то тогда со стороны тела В возникнет сила 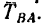 В задачах, как правило, рассматривают только эти две силы, приложенные к телам A и В (рис. 127, а).
В задачах, как правило, рассматривают только эти две силы, приложенные к телам A и В (рис. 127, а).
На рис. 127,6 показаны силы, приложенные только к стержню, т. е. показаны действия на стержень тел A и В.
Если два тела А и В связаны друг с другом при помощи так называемого внутреннего шарнира (рис. 128), то направление сил взаимодействия заранее неизвестно. Поэтому каждая из сил взаимодействия между телами (силы 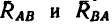 — предполoжительно
— предполoжительно
показаны на рис. 128 штриховыми векторами) заменяются составляющими 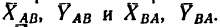 Причем
Причем 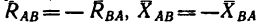 и
и 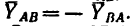
Задача №1
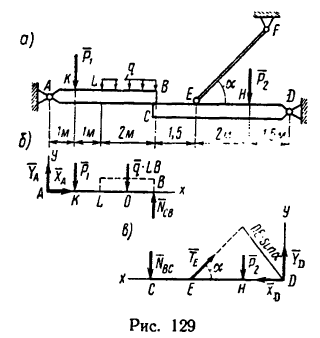
Балка АВ, имея в точке А шарнирное крепление, опирается в точке В на балку CD (рис. 129, а), которая удерживается в равновесии стержнем EF (в точках Е и F — шарнирные соединения) и шарниром D. Размеры и расположение нагрузок показаны на рисунке.
Определить реакции шарниров A, D и стержня EF. 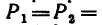 20 кн,
20 кн, 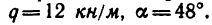
Решение.
1. Рассмотрим равновесие каждой балки. Для этого изобразим балки АВ и CD раздельно. На рис. 129, б изображена балка АВ с двумя нагрузками 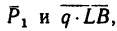 составляющими реакции шарнира
составляющими реакции шарнира 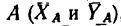 и реакцией опоры в точке
и реакцией опоры в точке 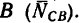
На рис. 129, в изображена балка CD, имеющая заданную нагрузку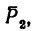 нагрузку
нагрузку 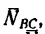 которая неизвестна, составляющие реакции шарнира
которая неизвестна, составляющие реакции шарнира 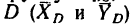 и реакцию
и реакцию 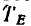 стержня EF.
стержня EF.
2. Рассмотрим равновесие балки АВ и составим уравнения (начинать решение задачи с рассмотрения равновесия балки CD пока не имеет смысла, так как в три уравнения равновесия, которые можно составить для плоской системы сил, войдут четыре неизвестные силы 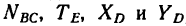 ):
):
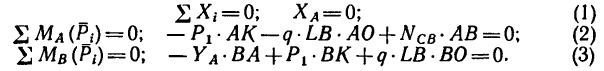
Из уравнения (1)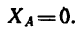
Из уравнения (2)
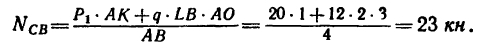
Из уравнения (3)
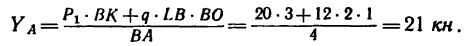
3. Теперь можно рассмотреть равновесие балки CD. Реакция балки CD, иными словами ее противодействие давлению балки АВ, уже известна: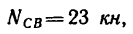
а значит известна и сила давления 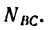 Таким образом,
Таким образом,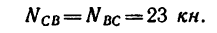
Учитывая это, составим уравнения равновесия для балки CD и решим их:
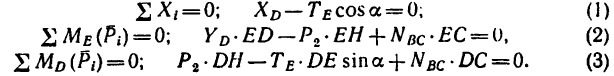
Из уравнения (3)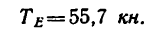
Из уравнения (1)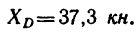
Из уравнения (2)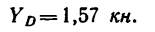
Реакция шарнира А определена выше: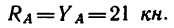
Проверку решения можно произвести при помощи любого из трех уравнений равновесия, составленного для всей сочлененной системы. В данном случае для проверки можно, например, использовать уравнение моментов относительно точки опоры одной балки на другую (точка В или С):
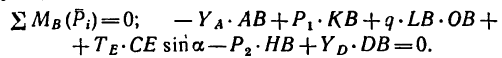
Подставив в уравнение значения величин, убедимся в том, что уравнение обратится в тождество. Значит, задача решена правильно.
Задача №2
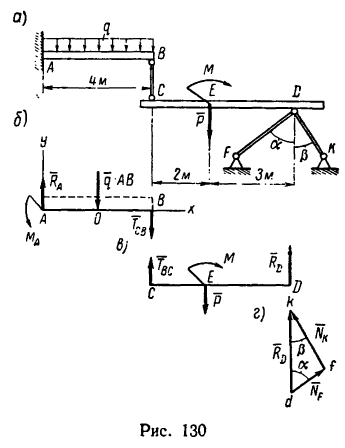
Балка АВ жестко заделана у точки А и нагружена по всей длине равномерно распределенной нагрузкой интенсивностью q = 8 кн/м (рис. 130, а). В точке В к балке шарнирно прикреплен стержень, ко второму концу которого также шарнирно прикреплена вторая балка CD, опирающаяся кроме того, в точке D на стержни DF и DK (соединения в точках D, F и К — шарнирные). Балка CD нагружена силой P = 10 кн и моментом М = 50 кн * м.
Определить реакции в заделке и усилия во всех трех стержнях, если стержень ВС вертикален и углы а=52°, 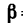 = 38°.
= 38°.
Решение.
1. Рассмотрим равновесие каждой балки отдельно.
К балке АВ приложены две нагрузки - по всей длине равномерно распределена нагрузка 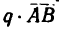 и в точке В сила
и в точке В сила 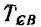 — переданное стержнем действие балки CD (рис. 130, б). Обе эти нагрузки уравновешиваются вертйкальной реакцией
— переданное стержнем действие балки CD (рис. 130, б). Обе эти нагрузки уравновешиваются вертйкальной реакцией 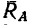 и реактивным моментом
и реактивным моментом 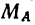 заделки (реакция
заделки (реакция 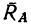 заделки не отклонена от вертикали, так как в данном случае нет усилий, стремящихся сместить балку АВ в горизонтальном направлении).
заделки не отклонена от вертикали, так как в данном случае нет усилий, стремящихся сместить балку АВ в горизонтальном направлении).
К балке CD приложены сосредоточенная сила Р и момент М. Обе нагрузки уравновешиваются реакциями,возникшими в стержнях ВС, DF и DK. Но так как соединительный стержень ВС расположен перпендикулярно к балке, а нагрузки не смещают ее в горизонтальном направлении, то равнодействующая реакций стержней DF и DK, приложенная в точке D, направлена перпендикулярно к балке (реакция 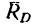 (рис. 130, в).
(рис. 130, в).
2. Составим уравнения равновесия для балки CD
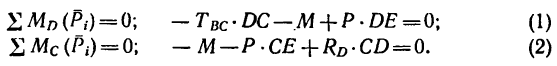
Из уравнения (1)
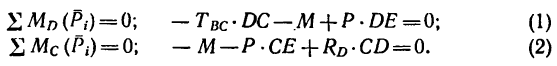
Знак минус показывает, что реакция 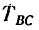 направлена не вверх, как показано на рис. 130, в, а вниз. Таким образом, стержень ВС не растянут, как предполагалось, а сжат. Значит и
направлена не вверх, как показано на рис. 130, в, а вниз. Таким образом, стержень ВС не растянут, как предполагалось, а сжат. Значит и 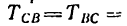
= - 4 кн, т. е. нагрузка 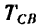 на балку АВ действует вверх, а Не вниз, как показано на рис. 130, б.
на балку АВ действует вверх, а Не вниз, как показано на рис. 130, б.
Из уравнения (2)
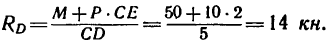
3. Реакция 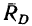 является равнодействующей реакций
является равнодействующей реакций 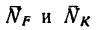 стержней DF и DK- Найдем эти реакции из рассмотрения треугольника dkf (рис. 130, г), построенного на силе
стержней DF и DK- Найдем эти реакции из рассмотрения треугольника dkf (рис. 130, г), построенного на силе 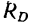 (см. задачу 87-14, решение 2).
(см. задачу 87-14, решение 2).
Треугольник dkf прямоугольный, так как 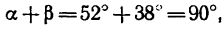 следовательно,
следовательно,
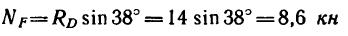
(стержень ED сжат, так как реакция направлена от стержня к шарниру D):
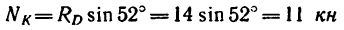 (стержень KD также сжат).
(стержень KD также сжат).
Таким образом, усилия во всех стержнях найдены и все стержни сжаты.
4. Для определения реакций в заделке нужно составить уравнения равновесия для балки АВ (см. рис. 130, б):
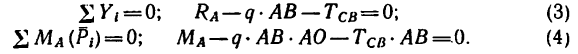
Из уравнения (3) находим RA (учитывая, что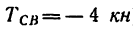 ):
):
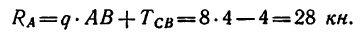
Из уравнения (4)
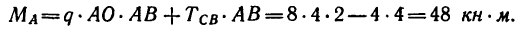
Проверку решения рекомендуется выполнить самостоятельно.

При решении задач, в которых сочленение тел произведено при помощи промежуточного шарнира, целесообразно сначала составить уравнения равновесия для всей системы, а затем добавить к ним уравнение моментов сил относительно промежуточного шарнира для одного из тел сочлененной системы.
Покажем это на примере следующей задачи.
Задача №3
Балки 1 и 2, шарниром С соединенные между собой, шарнирно прикреплены к неподвижным опорам в точках А и В (рис. 131, а). Длина балок одинакова: АС=ВС=4 м. Балка 1 в точке D Нагружена вертикальной силой 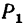 =100 кГ, а в точке £ —горизонтальной силой
=100 кГ, а в точке £ —горизонтальной силой 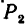 =80 кГ. Балка 2 в точке F нагружена перпендикулярной к ней силой
=80 кГ. Балка 2 в точке F нагружена перпендикулярной к ней силой 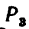 =200 кГ. Угол а=50°. Определить реакции шарниров А и В.
=200 кГ. Угол а=50°. Определить реакции шарниров А и В.
Решение.
1. Освободим балки от связей в точках А и В. Действие шарниров А и В заменим их реакциями, разложив каждую реакцию
на две составляющие по осям х и у (рис. 131, 6).
При рассмотрении равновесия обеих балок силы взаимодействия, возникающие в промежуточном шарнире С (составляющие этих сил показаны на рис. 131,6 штриховой линией), друг друга уравновешивают и поэтому могут не учитываться при составлении уравнений равновесия.
Таким образом, на систему балок 1 и 2 действуют всего семь внешних сил, расположенных в одной плоскости: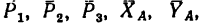
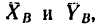 из них четыре последние силы неизвестны.
из них четыре последние силы неизвестны.
2. Для определения четырех неизвестных сил необходимо составить четыре уравнения.
Из условия равновесия системы балок составим три уравнения равновесия, приняв для третьего уравнения за центр моментов точку В:
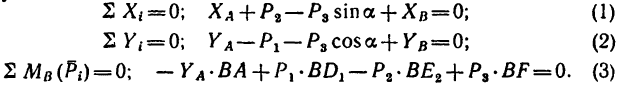
Четвертое уравнение составим исходя из равновесия балки 2 (на нее действует меньше сил, чем на балку 1):
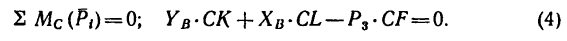
3. Определяем плечи сил, входящие в уравнения (3) и (4) (рис. 131, б):
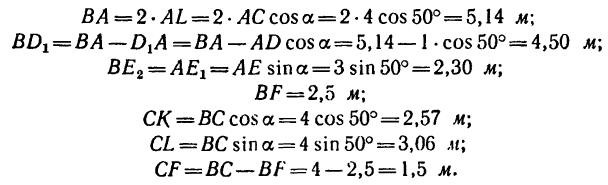
4 Теперь из уравнения (3) находим
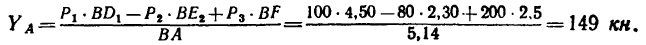
Из уравнения (2)
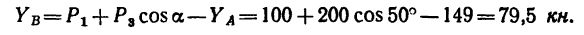
Из уравнения (4)
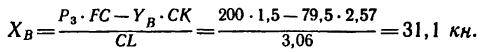
Из уравнения (I)
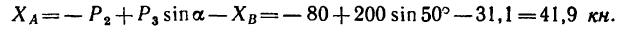 Проверку решения рекомендуется сделать самостоятельно при помощи уравнения моментов относительно точки С, составленного для всей системы.
Проверку решения рекомендуется сделать самостоятельно при помощи уравнения моментов относительно точки С, составленного для всей системы.
Если в соответствии с условием задачи требуется определить силу взаимодействия между балками в шарнире С, то теперь ее легко найти, рассмотрев равновесие одной из балок.
В следующей задаче рассмотрим равновесие сочлененной системы при наличии сил трения.
Задача №4
На наклонных плоскостях АС и ВС помещены два тела 1 и 2, связанные нитью, которая перекинута через блок D (рис. 132, а),
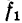 —коэффициент трения при взаимодействии тела 1 с плоскостью
—коэффициент трения при взаимодействии тела 1 с плоскостью 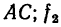 — коэффициент трения при взаимодействии тела 2 с плоскостью ВС. Вес первого тела G. При каком весе Q второго тела будет соблюдаться равновесие?
— коэффициент трения при взаимодействии тела 2 с плоскостью ВС. Вес первого тела G. При каком весе Q второго тела будет соблюдаться равновесие?
Решение.
1. Допустим, что тела 1 и 2, связанные нитью, поставлены на наклонные плоскости и находятся в равновесии.
2. Если вес тела 2 постепенно увеличивать, то при некотором значении- веса 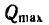 равновесие нарушится и оба тела начнут скользить вправо (тело 2— вниз по СВ, а тело 1 — вверх по АС).
равновесие нарушится и оба тела начнут скользить вправо (тело 2— вниз по СВ, а тело 1 — вверх по АС).
Изобразим оба тела с действующими на них силами в предельном состоянии (рис. 132, б) равновесия, т. е. в момент перед началом движения. На каждое тело действуют их веса 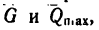 нормальные реакции наклонных плоскостей
нормальные реакции наклонных плоскостей 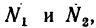 реакции нитей
реакции нитей 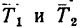 и силы трения
и силы трения 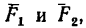 направленные в стороны, противоположные движению тел.
направленные в стороны, противоположные движению тел.
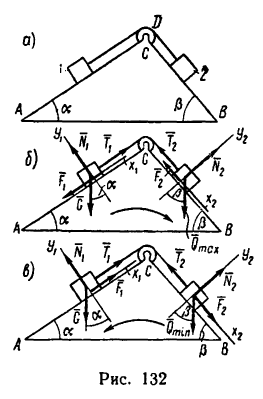
3. Рассмотрим равновесие каждого из тел в отдельности, пренебрегая их размерами, т. е. считая, что на тела действуют системы сходящихся сил.
Для сил, действующих на тело 1, получим такие уравнения равновесия:
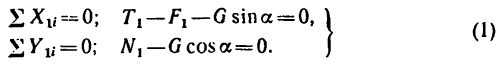
Для сил, действующих на тело 2, получим такие уравнения:
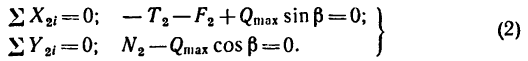
Из системы уравнений (1)
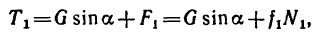
а так как 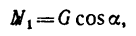
то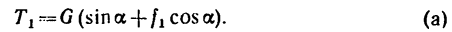
Из системы уравнений (2)
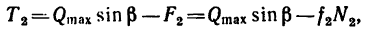
а так как
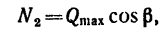
TO
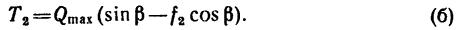
Натяжение нити, перекинутой через блок, по всей длине одинаково, поэтому
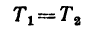
и, следовательно, правые части равенств (а) и (б) также равны между собой, т. с.
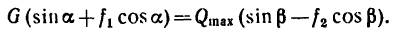
Отсюда определяем 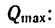
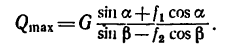
4. Теперь представим себе, что вес тела 2 постепенно уменьшается. При некотором значении веса 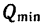 равновесие снова нарушится, но теперь оба тела начнут скользить влево (тело 1 — вниз по С А, а тело 2 —вверх но ВС).
равновесие снова нарушится, но теперь оба тела начнут скользить влево (тело 1 — вниз по С А, а тело 2 —вверх но ВС).
Изобразим на рис. 132, в оба тела с действующими на них силами в момент перед началом движения.
В этом случае но сравнению с предыдущим обе силы трения 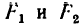 изменяют свое направление, так как изменяется направление скольжения тел.
изменяют свое направление, так как изменяется направление скольжения тел.
Рассматривая равновесия каждого из тел в отдельности, получаем следующие системы уравнений равновесия:
для тела 1
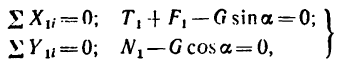
для тела 2
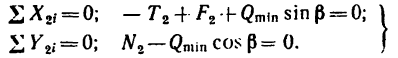
Решая эти системы уравнений так же, как и в предыдущем случае, находим 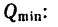
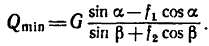
5. Таким образом, тела 1 и 2 находятся в равновесии при соблюдении условия
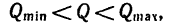
причем значения 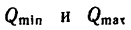 зависят от веса первого тела, от коэффициентов трения и от углов подъема наклонных плоскостей. Так, например, при
зависят от веса первого тела, от коэффициентов трения и от углов подъема наклонных плоскостей. Так, например, при 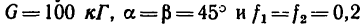 имеем:
имеем:
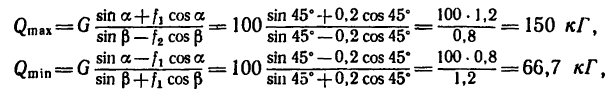
т. е. вес Q удовлетворяет условию
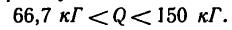
| Рекомендую подробно изучить предмет: |
| Ещё лекции с примерами решения и объяснением: |
- Равновесие пространственной системы сходящихся сил
- Определение положения центра тяжести тела
- Равномерное прямолинейное движение точки
- Равномерное криволинейное движение точки
- Разложение силы на две составляющие
- Определение равнодействующей сходящихся сил
- Равновесие сходящихся сил
- Равновесие трех непараллельных сил