Собственные тени поверхностей вращения в начертательной геометрии с примерами

Содержание:

Мы уже рассматривали построение собственных теней простейших геометрических поверхностей - цилиндра и конуса. Для цилиндра теневые образующие определяются двумя лучевыми плоскостями касательными к поверхности цилиндра. Для конуса теневые образующие определяются после построения падающей тени на плоскость основания.

В данной лекции рассмотрены рациональные приемы определения границ собственной тени прямого кругового цилиндра (рисунок 11.1) и кругового конуса (рисунок 11.2).

Тень цилиндра может быть построена без плана, т.е. без горизонтальной проекции, что очень удобно в архитектурном проектировании. Теневые образующие проходят через точки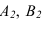

Рациональный прием построения собственной тени кругового конуса приведен на рисунке 11.2.

Для прямого конуса выполняются следующие построения (рисунок 11.2а). На основании конуса как на диаметре строится половина окружности. Из нижней точки окружности 1 проводится прямая 1,2 параллельная левой контурной образующей конуса. Из полученной точки 2 проводится прямые под углом 45° к основанию конуса до пересечения с окружностью в точках А и В. Спроецировав точки А и В на основание конуса, определим границы собственной тени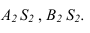

Для перевернутого конуса, обратного, построения аналогичны предыдущему (рисунок 11.26). Отличаются гем, что из точки 1 проводится прямая 1,2 параллельная правой образующей конуса.

Следует обратить внимание на величину части поверхности, находящейся в собственной тени: для прямого конуса она меньше половины, для обратного - больше.

Круговые конусы с наклоном образующих под углом 45° и 35° имеют важное значение при построении собственных теней поверхностей вращения.

Построение теней конуса с углом наклона образующей 45° приведено на рисунке 11.3.

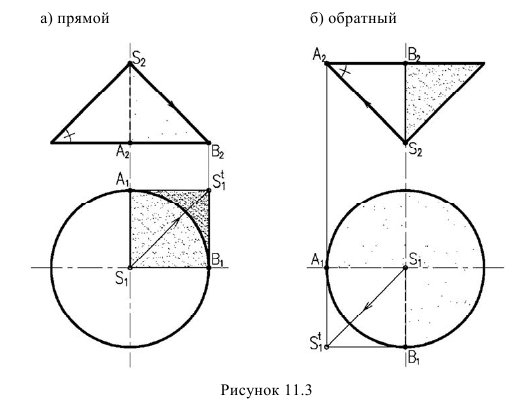
При построении падающей тени на плоскость основания фронтальная проекция луча совпадает на фронтальной проекции с контурной образующей конуса.

Для дальнейшего использования необходимо запомнить, что тень занимает: у прямого конуса - четверть поверхности, у обратного - три четверти поверхности.  

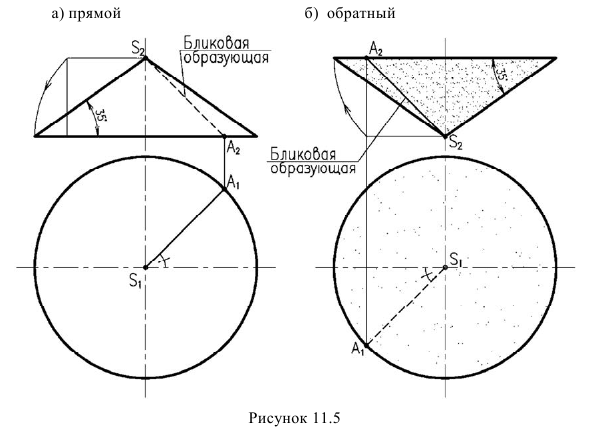
Построение теней конуса с углом наклона образующей 35° приведено на рисунке 11.5.

На рисунке 11.4 показано построение угла 35°.

ABCD - квадрат. Строим прямоугольник со стороной равной диагонали квадрата. Диагональ этого прямоугольника наклонена к горизонтали под углом 35°. -Рисунок 11.4

Из построения тени конуса с углом наклона образующей 35° видно, что границей тени будет служить одна образующая SA (теоретически), располагающаяся на фронтальной проекции под углом 45°. Практически прямой конус будет полностью освещен, а обратный -весь в тени. Образующая SA называется бликовой образующей. Положение образующих -границы тени таких двух конусов надо твердо усвоить, т.к. они будут часто встречаться в последующем, в качестве вспомогательных операций при построении теней, 

Тени поверхностей вращении. Способ касательных конусов и цилиндров

Построение контура собственной тени поверхностей вращения осуществляется при помощи способа касательных конусов и цилиндров. Этот способ заключается в следующем: берется конус или цилиндр касательный к поверхности вращения (т.е. описанный или вписанный в данную поверхность); на окружности касания отмечаются точки границы собственных теней касательных поверхностей; эти точки будут принадлежать и границе собственной тени заданной поверхности на той же окружности прикосновения, т.е. на той же параллели. Используя, таким образом, несколько конусов и цилиндров, определяется необходимое количество точек контура собственной тени.

Для поверхностей второго порядка достаточно восьми точек, используя один цилиндр (2 точки), прямой и обратный конус с образующей под углом 45° (4 точки), прямой и обратный конус с углом наклона образующей 35° (2 точки)

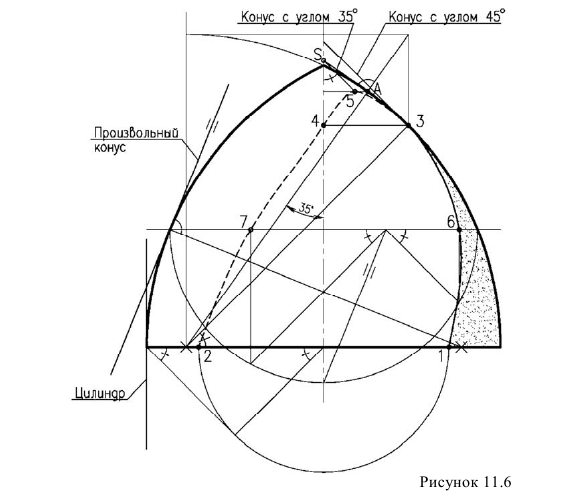
На рисунке 11.6 построения контура собственной тени выполнены следующим образом. Точки 1 и 2 получены как на цилиндре. Точки 3 и 4 найдены как на касательном конусе с углом наклона образующей 45°. Точку касания 3 точно можно определить, проведя нормаль (радиус) из центра дуги очерка поверхности под углом 45'\ Точка 4 лежит на одной горизонтали с точкой 3. Точка 5 найдена как на касательном конусе с углом наклона образующей 35°. Для ее построения из центра дуги очерка поверхности проводим прямую под углом 35Лк оси поверхности вращения. Точка пересечения с очерком даст точку А - точку касания конуса с образующей под углом 35°. Проводим из точки касания эту образующую перпендикулярно радиусу до пересечения с осью поверхности вращения в точке S. Из точки S проводим прямую под углом 45° до пересечения с основанием конуса (горизонталь проведенная через точку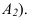

Промежуточные точки 6 и 7 найдены на линии касания конуса произвольного угла наклона образующей. Построение выполнено аналогично рисунку 11.2а.  

• Заказать чертежи

Тени форм, применяемых в архитектурном проектировании Тени сферы (рисунок 11.7)

Собственная тень проецируется на плоскость одинаковыми эллипсами. На рисунке 11.7 показано построение эллипса на фронтальной проекции. Точки / и 2 находятся как на цилиндре. Точки 3 и 4, 5 и 6 - как на прямом и обратном конусе с углом образующей 45°, причем диаметр 5,3 является большой ось эллипса. Точки 7 и 8 определяются на касательном конусе с углом образующей 35°. Точки 9 и 10 строятся симметрично 7 и 8 относительно большой оси. Точки 11 \\ 12 принадлежат малой оси эллипса, которая перпендикулярна большой оси 5,3. Построение точек осуществляется следующим образом. Из точки 5 проводим дугу радиусом сферы до пересечения с контуром. Полученные точки соединяем с точкой 3. Эти прямые пересекут малую ось в точках 11 и 12.

Тени тора (валика) (рисунок 1 1.8).

Построение контура собственной тени на торе осуществляется по восьми точкам.

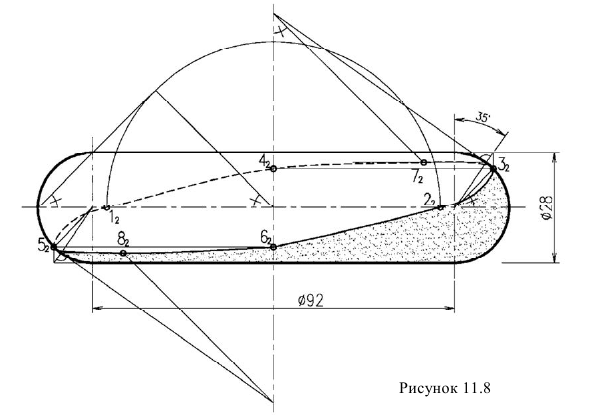
Точки 1 и 2 определяются как на цилиндре. Точки 3 и 4, 5 и 6 определяются как на прямом и обратном конусе с углом наклона образующей 45°. Точки 7 и 8 получены на касательном прямом и обратном конусе с углом наклона образующей 35°. Необходимо помнить, что вершина конуса всегда лежит на оси поверхности вращения.

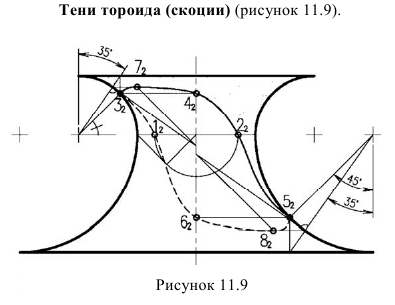
Построение контура собственной тени скопи и осуществляется также по восьми точкам. Только касательные конусы и цилиндр являются вписанными в данную поверхность. Точки 1 и 2 находятся как на цилиндре. Точки 3 и 4, 5 и 6 как на обратном и прямом конусе, соответственно, с углом наклона образующей 45°. Высшая и низшая точки 7 и 8 определяются с использованием касательных конусов с углом наклона образующей под углом 35°.