
Сложение скоростей в физике - формулы и определения с примерами
Сложение скоростей:
В повседневной жизни мы часто видим, как одни тела движутся относительно других движущихся тел. Например, стюардесса перемещается по салону летящего самолета, человек идет по движущемуся эскалатору (рис. 66), катер пересекает реку с быстрым течением и т. д.
Каковы закономерности таких движений?

Проведем опыт:
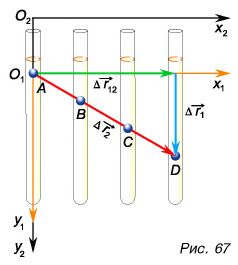
В вертикальную стеклянную трубку, заполненную вязкой жидкостью (например, сахарным сиропом), опустим металлический шарик (рис. 67). Трубку будем равномерно перемещать относительно школьной доски в горизонтальном направлении.
Систему отсчета с осями координат 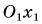 и
и 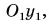 связанную с трубкой, назовем движущейся, а систему отсчета с осями
связанную с трубкой, назовем движущейся, а систему отсчета с осями 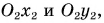 связанную с доской, — неподвижной.
связанную с доской, — неподвижной.
Наблюдая за движением шарика, будем отмечать на доске его положения через каждые 10 с (точки А, В, С, D).
Из рисунка 67 видно, что относительно трубки шарик за 30 с совершил перемещение 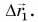 За это время трубка совершила перемещение
За это время трубка совершила перемещение 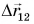 относительно школьной доски. Видно также, что перемещение
относительно школьной доски. Видно также, что перемещение 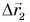 шарика относительно доски равно векторной сумме перемещений
шарика относительно доски равно векторной сумме перемещений 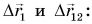
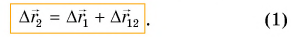
Перемещение тела относительно неподвижной системы отсчета равно векторной сумме его перемещения относительно движущейся системы и перемещения движущейся системы относительно неподвижной.
Все эти перемещения произошли за один и тот же промежуток времени 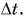 Разделив в формуле (1) каждое из перемещений на
Разделив в формуле (1) каждое из перемещений на 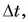 получим:
получим:

Вектор 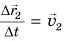 скорость движения шарика относительно доски (неподвижной системы отсчета), вектор
скорость движения шарика относительно доски (неподвижной системы отсчета), вектор 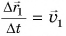 — скорость движения шарика относительно трубки (движущейся системы отсчета), а вектор
— скорость движения шарика относительно трубки (движущейся системы отсчета), а вектор 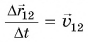 — скорость, с которой трубка (движущаяся система отсчета) перемещается относительно доски (неподвижной системы отсчета). Таким образом, из (2) следует:
— скорость, с которой трубка (движущаяся система отсчета) перемещается относительно доски (неподвижной системы отсчета). Таким образом, из (2) следует:

Скорость тела в неподвижном системе отсчета равна векторной сумме его скорости относительно движущейся системы и скорости движущейся системы относительно неподвижной.

Это утверждение называют законом сложения скоростей Галилея.
Закон сложения скоростей (3) используется при решении многих практических задач. Он позволяет рассчитать скорость самолета, заходящего на посадку при сильном ветре (рис. 68), скорость движения теплохода но реке (рис. 69) и т. д.

Главные выводы
- Перемещение тела относительно неподвижной системы отсчета равно векторной сумме его перемещения относительно движущейся системы и перемещения движущейся системы относительно неподвижной.
- Скорость тела в неподвижной системе отсчета равна векторной сумме его скорости относительно движущейся системы и скорости движущейся системы относительно неподвижной.
Пример решения задачи:
Путь от одной пристани до другой моторная лодка прошла по течению реки за время 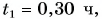 а обратный путь — за время
а обратный путь — за время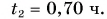 Модуль скорости течения воды
Модуль скорости течения воды 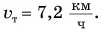 Определите модуль скорости движения лодки относительно воды, считая его постоянным.
Определите модуль скорости движения лодки относительно воды, считая его постоянным.

Решение
Сделаем рисунок к задаче (рис. 70).
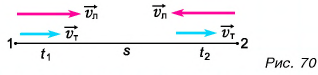
Относительно берега лодка плыла по течению (от пристани 1 к пристани 2) со скоростью, модуль которой 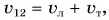 а обратно (от пристани 2 к пристани 1) — со скоростью, модуль которой
а обратно (от пристани 2 к пристани 1) — со скоростью, модуль которой 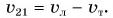
Значит, путь от пристани 1 до пристани 2: 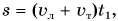 а путь от пристани 2 до пристани 1:
а путь от пристани 2 до пристани 1: 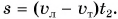 Приравнивая пути, получим:
Приравнивая пути, получим: 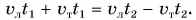
Отсюда
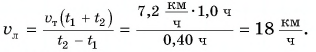
Ответ: 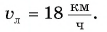
| Рекомендую подробно изучить предметы: |
| Ещё лекции с примерами решения и объяснением: |